13.3 GOVERNING FACTORS IN SOIL HEAT FLOW
The foregoing discussion has served to illustrate the need for a quantitative grasp of a soil temperature distribution. We now ask what properties of the soil and the general environment are important in determining this distribution. Once we know these properties, equations incorporating them can be derived, and (hopefully) solutions for various conditions can be found.
First, consider some actual observations of soil temperature measurements made at several depths beneath the soil over a period of several days (Fig. 13.2). Notice that at any depth the temperature is an almost periodic function of time. By this it is meant that the temperature trace (wave) repeats itself (almost) at regular intervals, in this case approximately every 24 hours. This time interval is called the period of the temperature wave, a variation with a periodicity of 24 hours being termed a diurnal variation. In addition to this time dependence, large differences in temperature are also evident between various depths. As one goes deeper, the amplitude of the wave is rapidly damped out. There is also a time (phase) lag associated with the occurrence of the maxima (or minima) of the temperature wave as depth increases.
These observations allow us to form a rather convincing hypothesis concerning the controlling variables. The observed diurnal heating cycle is no doubt linked to solar heating at the soil surface. Evidence for this is presented in Fig. 13.3, where it is apparent that soil temperature is strongly correlated with solar radiation. In fact, solar radiation is the energy source driving the flow of heat in the soil. (As will be shown later, it is this flow of heat which determines the temperature distribution.) The increasing phase lag as a function of depth is again quite evident, as it was in Fig. 13.2. It seems reasonable to hypothesize that the lag is due to the finite amount of time required for energy (as heat) to move down from the surface and heat up the soil profile. In turn, the speed or rate of energy flow is determined by a quality unique for a given material, known as its thermal conductivity (k). As the name implies, thermal conductivity is a measure of a particular substance’s ability to transmit heat. However, more information is required to completely specify the temperature variation. This is because, for a given amount of heat absorbed by various substances, different temperature increases will be observed. Hence the term heat capacity is introduced, and it may be thought of as the ratio of heat absorbed to change in temperature for a given mass of material.
In a very qualitative sense, we have described what appear to be the pertinent quantities involved in determining the soil temperature distribution, based simply on reason and observations (with just a little prior knowledge to guide the way). It remains now to formalize the relationship between heat flow and temperature, to develop the equations describing these processes (with emphasis on the simplifying assumptions involved), and finally to investigate the utility of this more formalized approach.
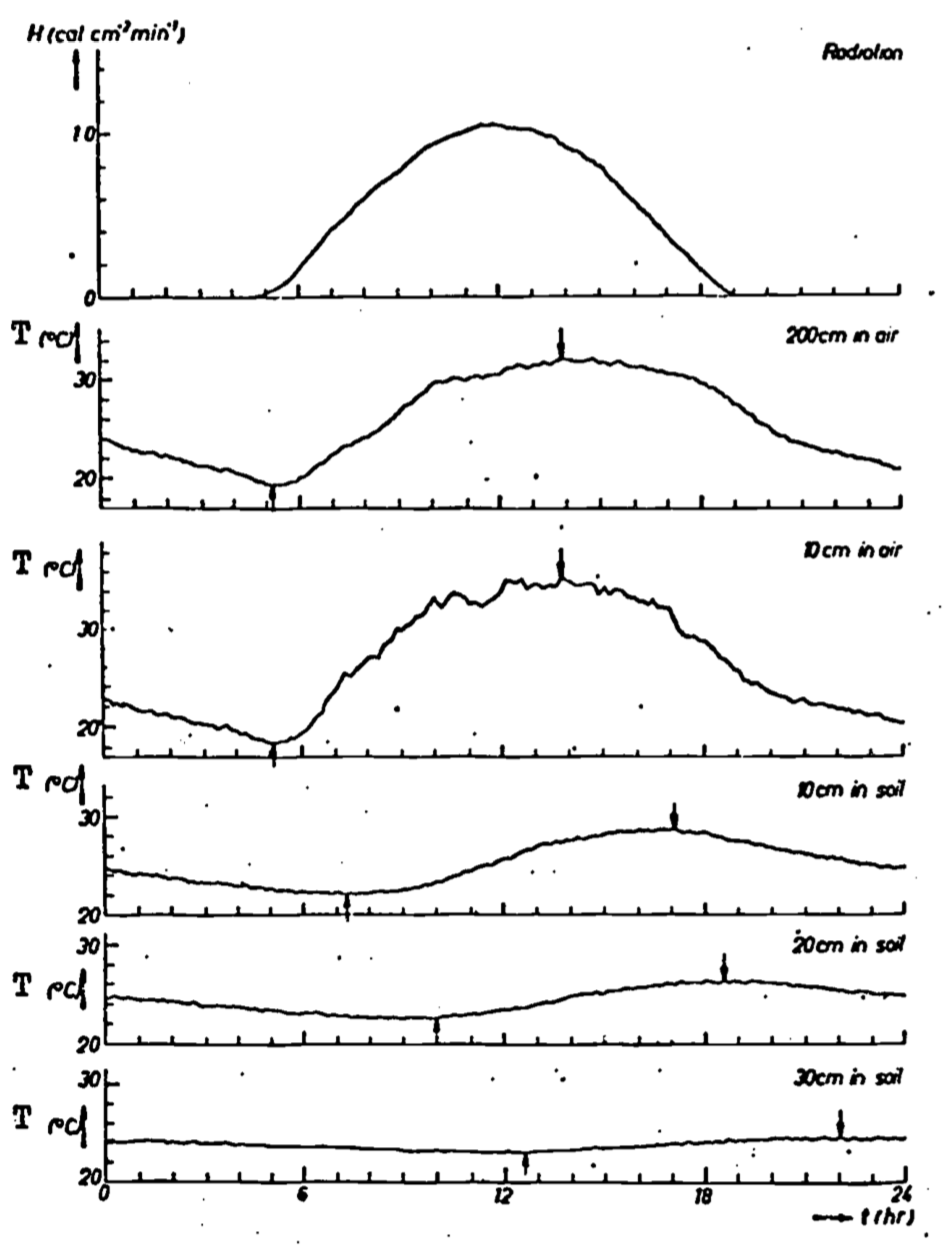
Figure 13.3: Short-wave solar radiation, air temperatures and soil temperatures for a clay soil with grass cover at Wageningen, the Netherlands, on a bright day, August 17, 1947. The extreme values of the temperatures are indicated by arrows (from Van Wijk 1966).