Poglavlje 4 Opisna statistika
Opisna (deskriptivna) statistika je prvi korak u analizi varijabli rezultata istraživanja.
Opisna statistika uključuje niz statističkih parametara koji opisuju varijable. Kao prvi korak u prikazu podataka koriste se upravo parametri opisne statistike i slikovni prikazi raspodjela podataka.
Za potrebe opisne statistike biti će prikazani načini i mogućnosti različitih paketa poput psych (Revelle, 2021), lessR (Gerbing et al., 2021) i DescTools (Signorell, 2021).
4.1 Mjere centralne tendencije
Najčešće mjere centralne tendencije koje se koriste u praksi su:
aritmetička sredina (mean)
centralna vrijednost (medijan)
dominantna vrijednost (mod)
geometrijska sredina
harmonična sredina
Aritmetička sredina predstavlja zbroj svih vrijednosti podijeljen brojem (količina) vrijednosti. Pri korištenju aritmetičke sredine treba voditi računa o aritmetičkoj sredini populacije (\(\mu\)) i aritmetičkoj sredini uzorka (\(\bar{X}\)) što svakako nije isto. U praksi gotovo uvijek radimo s aritmetičkom sredinom uzorka koju označavamo s velikim slovom M ili (\(\bar{X}\)). Aritmetičku sredinu populacije u literaturi nazivamo i pravom aritmetičkom sredinom jer pri korištenju statističkih testova ili provjeri valjanosti hipoteza, aritmetičku sredinu populacije odmjeravamo ili procjenjujemo temeljem aritmetičke sredine uzorka.
Nekoliko je uvjeta za primjenu aritmetičke sredine:
Zahtjeva numeričke podatke i normalnu raspodjelu rezultata mjerenja.
Prikladnija mjera centralne tendencije za varijable na intervalnim i omjernim mjernim ljestvicama.
Prikladnija mjera centralne tendencije za veći uzorak (N>20).
Uz aritmetičku sredinu u pravilu se navodi standardna devijacija kao mjera varijabilnosti rezultata.
Prije uporabe i interpretacije svakako napraviti slikovni prikaz podataka dotične varijable.
Aritmetička sredina je jedna od mjera centralne tendencije koja se nekritički koristi u praksi tj. statističko metodološki problematično (Speelman & McGann, 2013).
Najjednostavnije korištenje aritmetičke sredine u R jeziku je uporabom funkcije mean(). Prilikom korištenja navedene funkcije valja znati i primjenu argumenta na.rm=TRUE što znači korištenje izračuna ignorirajući missing value. U slijedećem primjeru jednostavno možemo pridjeliti varijabli proba_x vrijednosti od 1 do 10 te izračunati aritmetičku sredinu.
proba_x <- c(1,2,3,4,5,6,7,8,9,10)
mean(proba_x)## [1] 5.5Centralna vrijednost (C) nalazi se točno u sredini niza vrijednosti poredanih od najmanje prema najvećoj. Zahtjeva numeričke podatke. Računa se kada raspodjela (distribucija) rezultata mjerenja odstupa od normalne. Prikladna za manje uzorke čiji rezultati znatno odstupaju, variraju. Uz centralnu vrijednost kao mjeru centralne tendencije u pravilu se navodi absolutno odstupanje od medijana (MAD, median absolute distance) i/ili ukupni raspon (min, max, TR = max - min). Centralna vrijednost se izračunava pomoću funkcije median().
proba_y <- c(1,2,3,3,3,3,3,4,5,6,6,7,8,9,10)Dominantna vrijednost (D) je vrijednost čija je učestalost najveća u odnosu na druge vrijednosti varijable. Računa se na učestalostima ili frekvencijama. Nije važna raspodjela podataka jer u tom slučaju normalna raspodjela ne postoji. U pravilu se koristi kada su varijable kvalitativne, kategorijske ili se nalaze na nominalnoj ili najviše ordinalnoj mjernoj ljestvici. U tom slučaju, ograničeni smo jer ne možemo korisiti aritmetičku sredinu ili medijan. Dominantna vrijednost pomoću funkcije nije uključena u base paket od R jezika, već trebamo dohvatiti paket modeest i koristiti funkciju mfv().
library(modeest)
mfv(proba_y)## [1] 3Ukoliko želimo koristiti zbirni izvještaj deskriptivne statistike, tada može koristiti paket psych. U tom slučaju dobijemo niz vrijednosti deskriptivne statistike, u ovom slučaju varijable proba_y ili cijele datoteke s podatcima.
library(psych)
describe(proba_y)## vars n mean sd median trimmed mad min max range
## X1 1 15 4.87 2.7 4 4.77 2.97 1 10 9
## skew kurtosis se
## X1 0.46 -1.16 0.7Harmonična vrijednost ili harmonijska sredina računa se na numeričkim vrijednostima. Izračun se temelji na podjeli broja ispitanika ili mjera s recipročnom vrijednosti svake pojedine vrijednosti ispitanika ili mjere. Drugim riječima, harmonična vrijednost je recipročna vrijednost aritmetičke sredine recipročnih vrijednosti. Recipročna vrijednost je 1/n.
Kao primjer opisne statistike, među ostalim, koristit će se objavljeni podaci kliničkog istraživanja učinka uporabe deksametazona na kognitivne funkcije nakon kardijalnih operacija (Glumac et al., 2017).
library(psych)
describe(sat.act) #primjer datoteke ugrađene u paket psych za demonstraciju## vars n mean sd median trimmed mad
## gender 1 700 1.65 0.48 2 1.68 0.00
## education 2 700 3.16 1.43 3 3.31 1.48
## age 3 700 25.59 9.50 22 23.86 5.93
## ACT 4 700 28.55 4.82 29 28.84 4.45
## SATV 5 700 612.23 112.90 620 619.45 118.61
## SATQ 6 687 610.22 115.64 620 617.25 118.61
## min max range skew kurtosis se
## gender 1 2 1 -0.61 -1.62 0.02
## education 0 5 5 -0.68 -0.07 0.05
## age 13 65 52 1.64 2.42 0.36
## ACT 3 36 33 -0.66 0.53 0.18
## SATV 200 800 600 -0.64 0.33 4.27
## SATQ 200 800 600 -0.59 -0.02 4.41Ukoliko želimo napraviti nešto ljepšu tablicu, možemo to napraviti pomoću paketa kableExtra (Zhu, 2021).
library(kableExtra)
dobra_tbl <- describe(sat.act)
kable(dobra_tbl)| vars | n | mean | sd | median | trimmed | mad | min | max | range | skew | kurtosis | se | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| gender | 1 | 700 | 1.647 | 0.4782 | 2 | 1.684 | 0.000 | 1 | 2 | 1 | -0.6145 | -1.6247 | 0.0181 |
| education | 2 | 700 | 3.164 | 1.4254 | 3 | 3.307 | 1.483 | 0 | 5 | 5 | -0.6808 | -0.0749 | 0.0539 |
| age | 3 | 700 | 25.594 | 9.4986 | 22 | 23.863 | 5.930 | 13 | 65 | 52 | 1.6431 | 2.4243 | 0.3590 |
| ACT | 4 | 700 | 28.547 | 4.8236 | 29 | 28.843 | 4.448 | 3 | 36 | 33 | -0.6564 | 0.5350 | 0.1823 |
| SATV | 5 | 700 | 612.234 | 112.9026 | 620 | 619.454 | 118.608 | 200 | 800 | 600 | -0.6438 | 0.3252 | 4.2673 |
| SATQ | 6 | 687 | 610.217 | 115.6393 | 620 | 617.254 | 118.608 | 200 | 800 | 600 | -0.5929 | -0.0178 | 4.4119 |
Pomoću paketa kableExtra možemo dodatno preurediti tablicu te eksportirati u različite formate. Za dodatne informacije konzultirajte priručnik u pdf formatu od navedenog paketa.
Osim pomoću paketa psych, opisna statistika i izgled raspodjele lijepo se može prikazati pomoću drugih paketa lessR ili DescTools (Signorell, 2021).
library(lessR)
dob_sat.act <- sat.act$age
Histogram(dob_sat.act)## >>> Note: dob_sat.act is from the workspace, not in a data frame (table)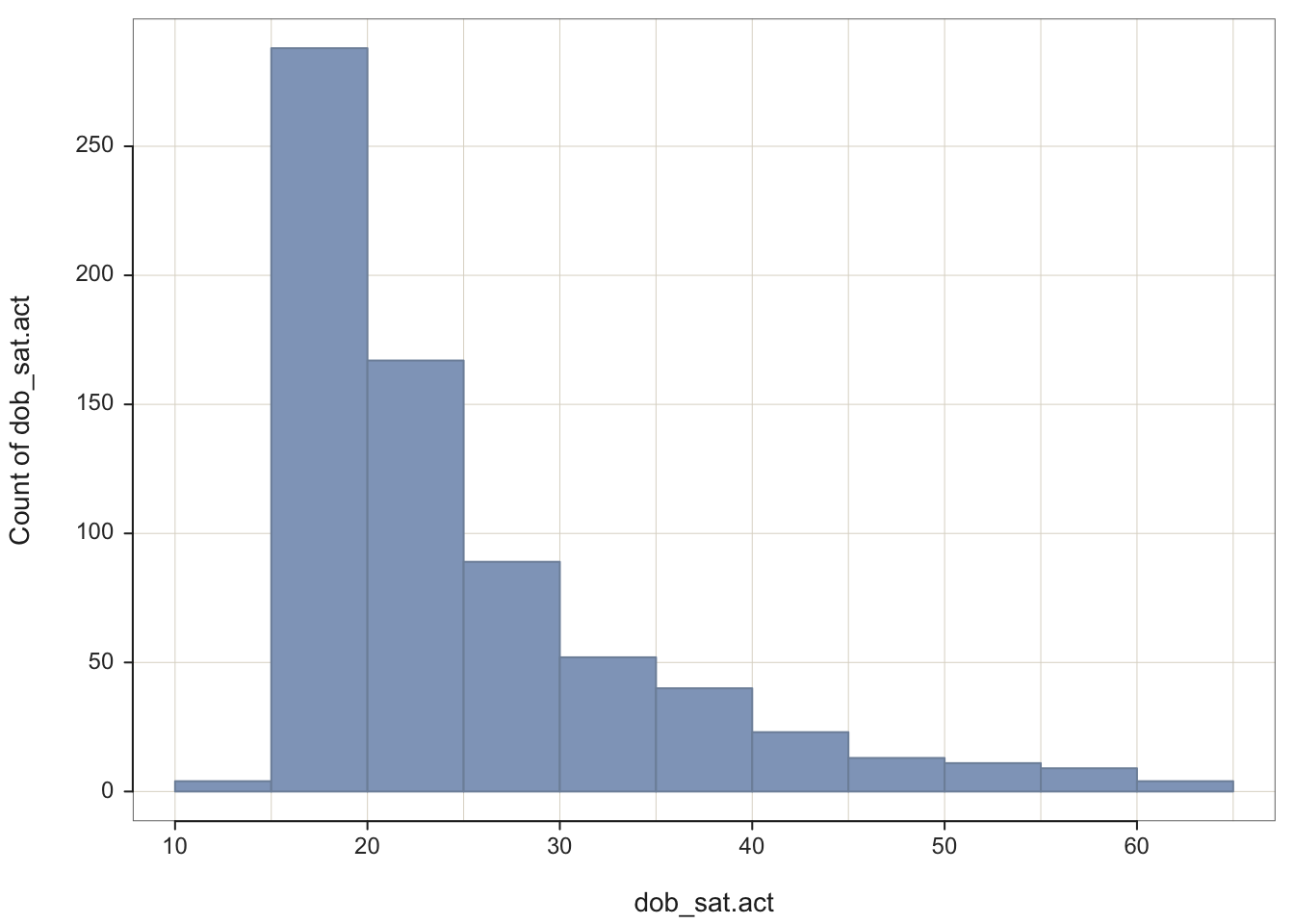
## >>> Suggestions
## bin_width: set the width of each bin
## bin_start: set the start of the first bin
## bin_end: set the end of the last bin
## Density(dob_sat.act) # smoothed density curves plus histogram
## Plot(dob_sat.act) # Violin/Box/Scatterplot (VBS) plot
##
##
## --- dob_sat.act ---
##
## n miss mean sd min mdn max
## 700 0 25.59 9.50 13.00 22.00 65.00
##
##
## (Box plot) Outliers: 39
##
## Small Large
## ----- -----
## 65.0
## 62.0
## 61.0
## 61.0
## 58.0
## 58.0
## 58.0
## 57.0
## 57.0
## 57.0
## 57.0
## 57.0
## 56.0
## 55.0
## 55.0
## 55.0
## 55.0
## 54.0
##
## + 21 more outliers
##
##
## Bin Width: 5
## Number of Bins: 11
##
## Bin Midpnt Count Prop Cumul.c Cumul.p
## -------------------------------------------------
## 10 > 15 12.5 4 0.01 4 0.01
## 15 > 20 17.5 288 0.41 292 0.42
## 20 > 25 22.5 167 0.24 459 0.66
## 25 > 30 27.5 89 0.13 548 0.78
## 30 > 35 32.5 52 0.07 600 0.86
## 35 > 40 37.5 40 0.06 640 0.91
## 40 > 45 42.5 23 0.03 663 0.95
## 45 > 50 47.5 13 0.02 676 0.97
## 50 > 55 52.5 11 0.02 687 0.98
## 55 > 60 57.5 9 0.01 696 0.99
## 60 > 65 62.5 4 0.01 700 1.00library(DescTools)
plot(Desc(d.pizza$temperature))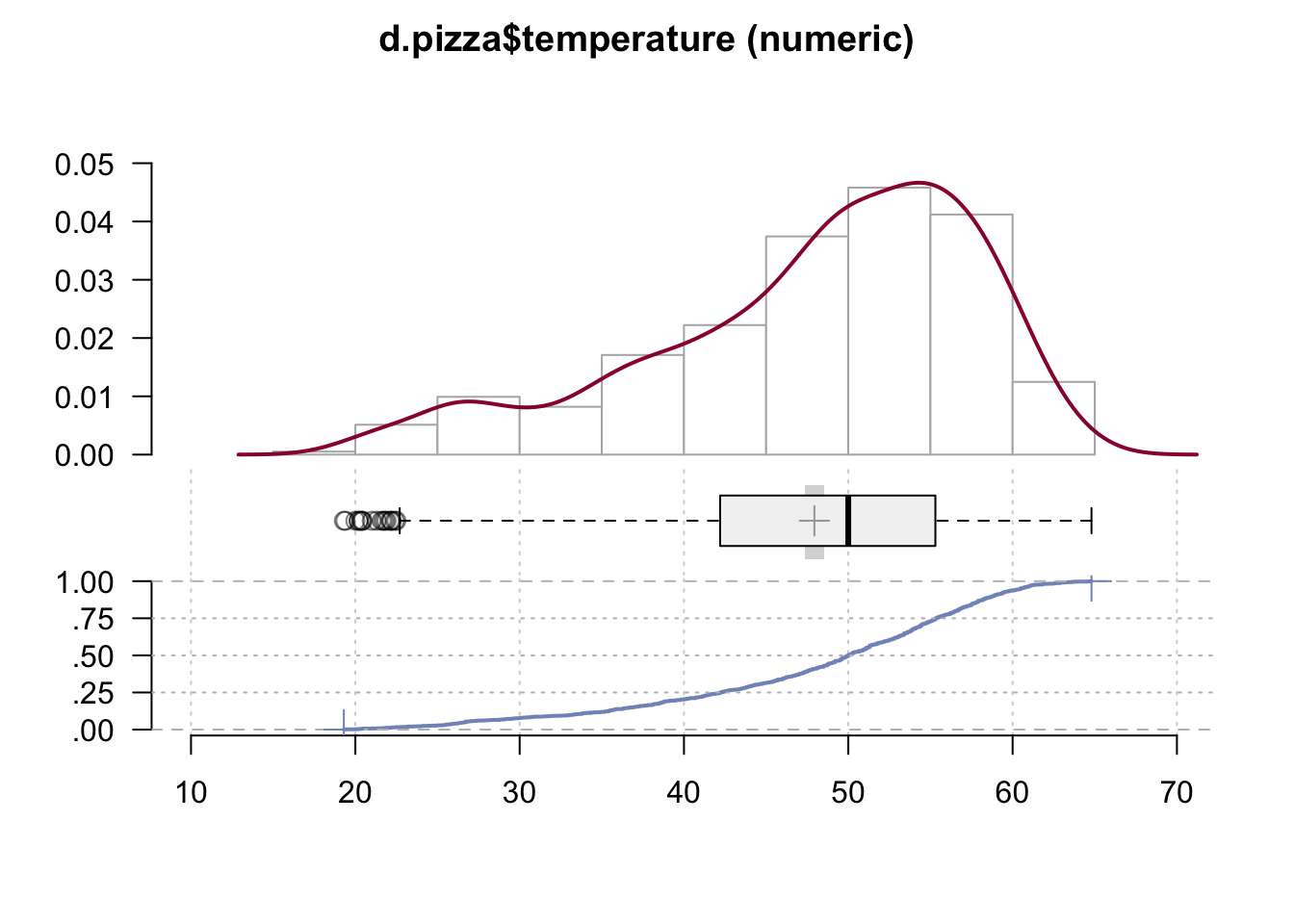
4.2 Mjere varijabilnosti, odstupanja
U praksi se koristi niz vrijednosti mjera varijabilnost kao što su:
ukupni (totalni) raspona,
koeficijent varijabilnosti,
absolutna udaljenost od medijana (MAD),
standardna devijacija (SD),
varijanca.
Uz aritmetičku sredinu u pravilu se koristi standardna devijacija.
\[\sigma = \sqrt{\frac{\sum\limits_{i=1}^{n} \left(x_{i} - \bar{x}\right)^{2}} {n-1}}\]
Mjera raspršenja podataka čija je raspodjela / distribucija normalna. Tri standardne devijacije ispod aritmetičke sredine i tri iznad aritmetičke sredine. Kvadrat standardne devijacije je varijanca. Koeficijent varijacije (CV) je standardna devijacija izražena u postocima od aritmetičke sredine.
4.3 Normalna raspodjela
Normalna raspodjela je jedan od središnjih pojmova u primjeni statistike u znanosti. Normalna raspodjela vezana je uz pojam centralnog graničnog teorema (engleski: Central Limit Theorem) U R-u imamo nekoliko vrlo vrijednih načina prikaza rezultata istraživanja ili simulacije podataka. Za simulaciju rezultata istraživanja možemo prikazati normalnu raspodjelu pomoću funkcije rnorm.
### Histogramski prikaz simulacija rezultata istraživanja
### na 100 ispitanika (n=100), aritmetička sredina 100 i standardna devijacija 10
hist(rnorm(100, mean = 100, sd = 10))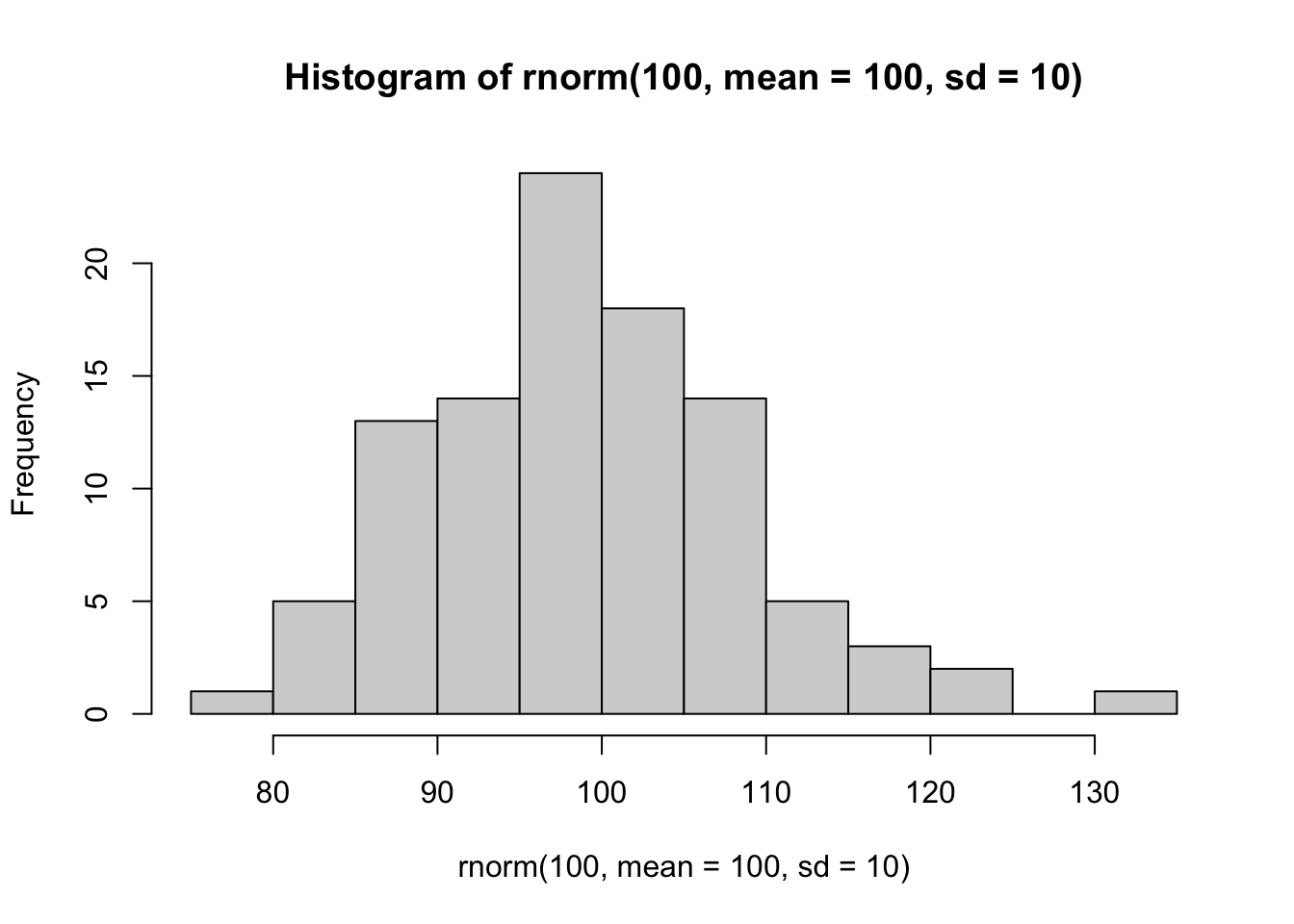
## kako se mijenja izgled raspodjele ovisno o broju ispitanika povećavajući
## broj ispitanika 10 puta
hist(rnorm(1000, mean = 100, sd = 10))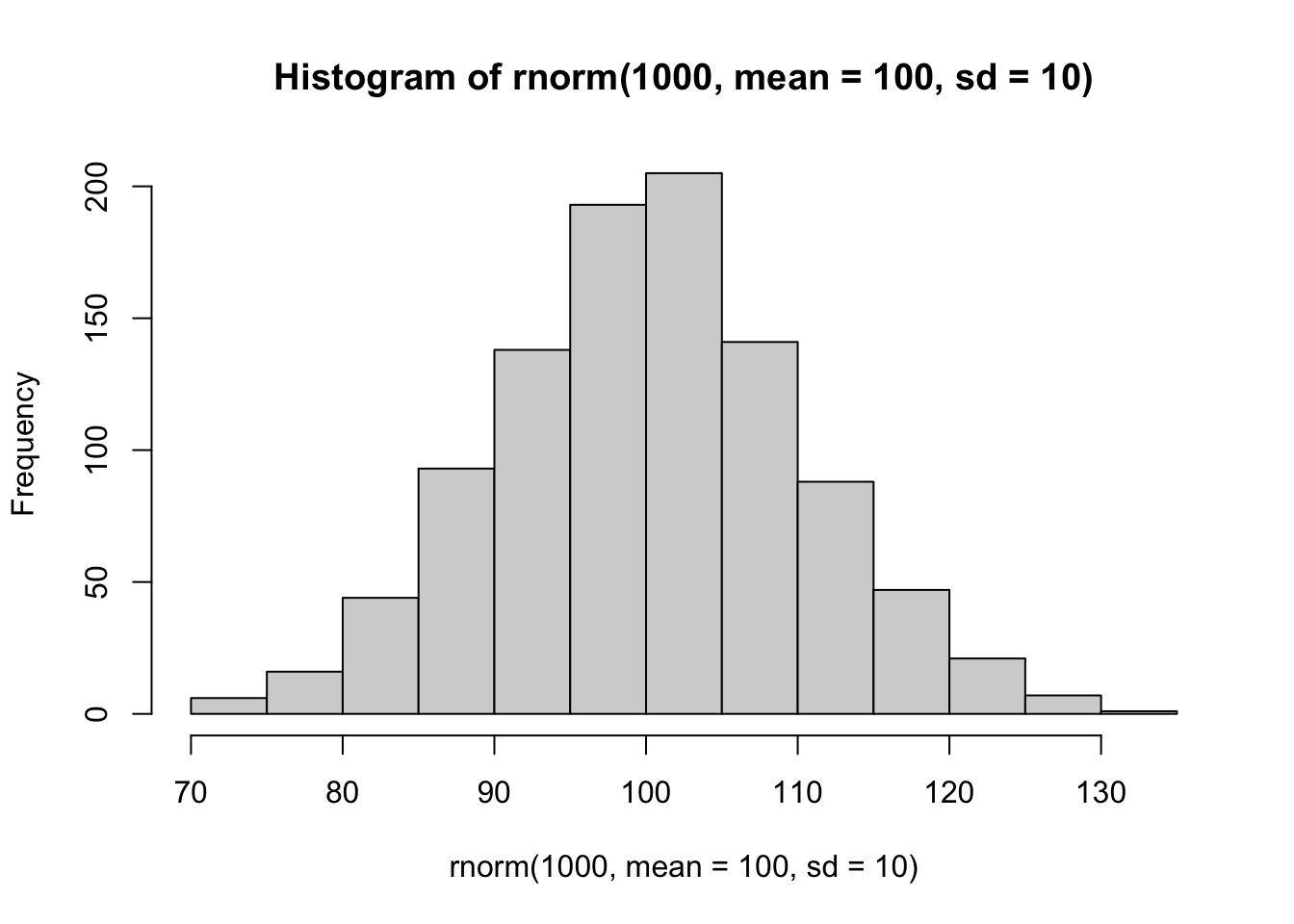
## povećavajući broj ispitanika 100 puta
hist(rnorm(10000, mean = 100, sd = 10))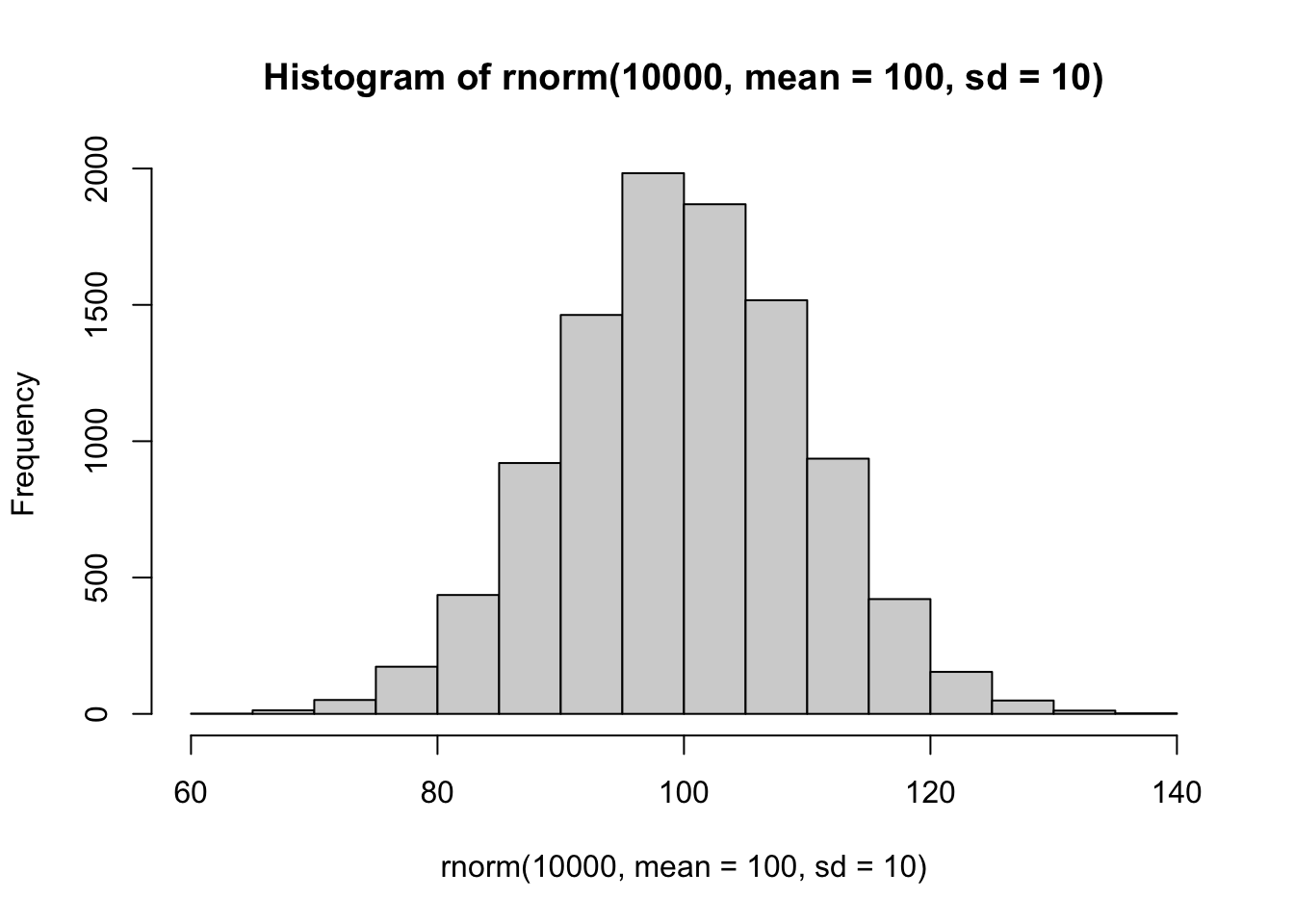
Iz navedenih primjera vidimo promjene oblika raspodjela mijenjanjem veličine uzorka.
4.3.1 Procjene simetričnosti
Kod potpuno simetrične raspodjele, aritmetička sredina, centralna vrijednost i dominantna vrijednost su jednake vrijednosti. Ukoliko raspodjela rezultata odstupa od normalne, tada navedene mjere centralne tendencije su radzličite vrijednosti.
Skewness je mjera asimetričnosti te ukoliko je ta vrijednost veća od -1 ili +1 tada možemo reći kako je raspodjela jako asimetrična. Ukoliko je vrijednost između -0.5 i 1 te između +0.5 i 1 tada kažemo kako je raspodjela umjereno asimetrična. Konačno, ako je vrijednost u rasponu između -0.5 i 0.5, dakle oko nula, tada možemo reći kako navedena raspodjela je približno normalna.
U slijedećem primjeru možemo jednostavno simulirati simetričnosti i odnose prema mjerama centralne tendencije. Varijablama proba_x, proba_y i proba_z dodijelimo niz vrijednosti kako slijedi i promotrimo što se događa sa vrijednosti skewness i kurtosis pomoću paketa psych i funkcije describe.
library(psych)
proba_x <- c(1,2,3,4,5,6,7,8,9,10)
describe(proba_x)## vars n mean sd median trimmed mad min max range
## X1 1 10 5.5 3.03 5.5 5.5 3.71 1 10 9
## skew kurtosis se
## X1 0 -1.56 0.96proba_y <- c(1,2,3,4,5,6,7,8,9,15)
describe(proba_y)## vars n mean sd median trimmed mad min max range
## X1 1 10 6 4.08 5.5 5.5 3.71 1 15 14
## skew kurtosis se
## X1 0.79 -0.25 1.29proba_z <- c(1,5,6,7,8,9,10,11,12,13)
describe(proba_z)## vars n mean sd median trimmed mad min max range
## X1 1 10 8.2 3.61 8.5 8.5 3.71 1 13 12
## skew kurtosis se
## X1 -0.48 -0.87 1.14Vrijednost kurtosis pokazuje u kojoj mjeri je raspodjela platikurtična ili leptokurtična. Ukoliko je vrijednost kurtosis ispod 3, tada je riječ o raspodjeli koja je u manjoj ili većoj mjeri spljoštenija tj. platikurtična. Vrijednost oko 3 podrazumijeva kako je raspodjela slična teorijskoj normalnoj raspodjeli.
4.4 Položaj i vjerojatnosti rezultata
R ima niz funkcija koje omogućavaju kvalitatno prikazivanje raspodjela te površina, vjerojatnosti i vrijednosti pojedinih rezultata.
Tako funkcija pnorm omogućava izračun površine i vjerojatnosti iznad određene vrijednosti normalne raspodjele. Ako zamislimo normalnu raspodjelu koeficijenata inteligencije (IQ) čija je aritmetička sredina 100 i devijacija 10, koliko je vjerojatno u slučajnom odabiru dobiti vrijednost veću od 110.
pnorm(110,mean=100,sd=10)## [1] 0.8413Funkcija qnorm izračunava obrnuto tj. koja je vrijednost u određenom percentilu normalne raspodjele. Tako npr. iz prethodnog primjera, koja vrijednost IQ pada točno na 80. percentil?
qnorm(0.80,mean=100,sd=10)## [1] 108.4Kako izgleda raspodjela kvocijenta inteligencije u histogramskom prikazu i interpolaciji normalne krivulje u prethodnom primjeru na 100 ispitanika.
x <- rnorm(100, mean=100, sd=10)
hist(x, probability=TRUE)
xy <- seq(min(x), max(x), length=100)
lines(xy, dnorm(xy, mean=100, sd=10))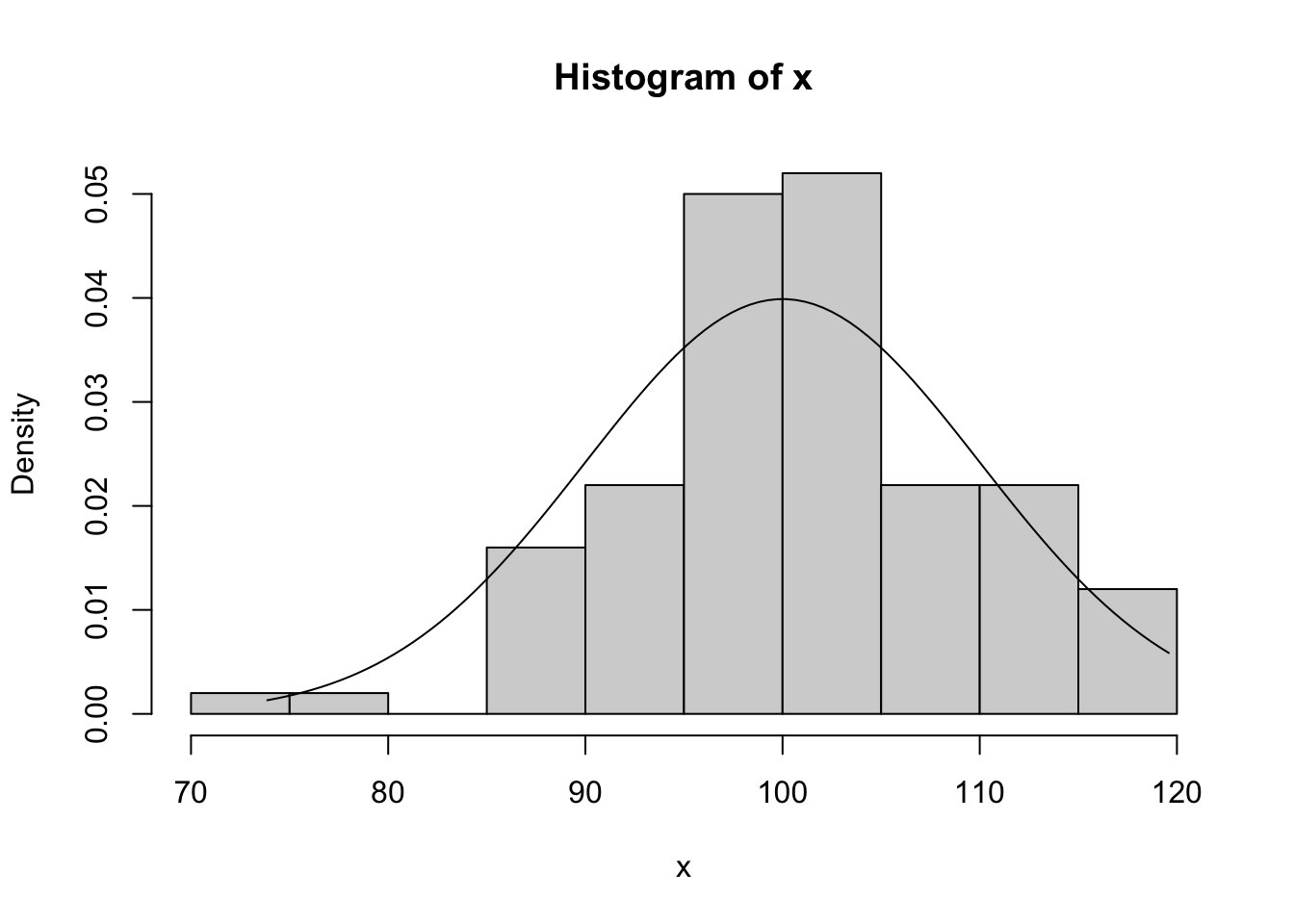
4.4.1 Centili, decili
Centile često koristimo za izražavanje položaja pojedinog rezultata neke varijable. Centili i decili za razliku od z-vrijednosti ne trebaju normalnu raspodjelu. Na neki način, možemo reći kako su centili i decili mjere položaja pojedinog rezultata u području neparametrijske statistike. Centili predstavljaju relativni rang. Centile i decile ne možemo zbrajati kao što je to slučaj kod z vrijednosti.
U R jeziku imamo ugrađenu funkciju quantile koja omogućava rad sa centilima.
Pretposatvimo u jednom primjeru mjerenje tjelesne težine na uzorku od 20 studentica.
tjelesna_tezina <- c(57, 54, 48, 63, 67, 62, 50, 73, 48, 51, 60, 70, 66, 62, 76, 59, 61, 55, 53, 71)
quantile(tjelesna_tezina)## 0% 25% 50% 75% 100%
## 48.00 53.75 60.50 66.25 76.00Korištenjem funkcije quantile bez pojedinih parametara unutar funkcije vrlo jednostavno dobivamo granice pojedinih kvartila za određeni raspon vrijednosti. Korištenjem funkcija možemo dobiti konkretne informacije za pojedinu vrijednost. U slijedećem koraku možemo dobiti granice raspodjela za pojedine decile.
quantile(tjelesna_tezina, prob = seq(0, 1, length = 11), type = 5)## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
## 48.0 49.0 52.0 54.5 58.0 60.5 62.0 64.5 68.5 72.0 76.0Dok, na istim podacima možemo dobiti granice npr. 35, 65 i 75 centil.
quantile(tjelesna_tezina, prob = c(0.35, 0.65, 0.75))## 35% 65% 75%
## 56.30 62.35 66.254.4.2 Z vrijednosti
Z-vrijednosti predstavljaju položaj pojedinačnog rezultata varijable. Z vrijednost se izražava u dijelovima standardne devijacije a što je jasno vidljivo i proizlazi iz formule.
\[\begin{equation} z=\frac{(x - \bar{X})}{SD} \tag{4.1} \end{equation}\]
Uz pomoć z-vrijednosti a koja se zasniva na standardnoj devijaciji mogu se ispravno uspoređivati rezultati što su ih ispitanici postigli u dva ili više testova.
Pri uporabi z vrijednosti treba imati na umu;
Aritmetička sredina i standardna devijacija definiraju normalnu raspodjelu. Prema tome, treba voditi računa pri uporabi z vrijednosti sva ograničenja i mogućnosti interpretacije normalne raspodjele i uporabe aritmetičke sredine i standardne devijacije
Treba nam informacija gdje je podatak ili rezultat u nizu
Možemo izračunati koliko je ispod a koliko iznad određene vrijednosti
U slučaju ‘kompozitnog’ rezultata – z vrijednosti omogućavaju ZBRAJANJE i ODUZIMANJE!
Moguće je uspoređivati rezultate mjerenja koji su dobiveni različitim mjerama (krivo mišljenje – usporedba apsolutnih vrijednosti!, na vrijednost utječe aritmetička sredina i standardna devijacija)
Ukoliko ‘pješke’ računamo z vrijednosti, tada pomoću tablice možemo izračunati površinu normalne raspodjele. Inače, pomoću funkcija na računalu možemo odrediti veličinu površine koja je ujedno i vjerojatnost.
U odnosu na druge koeficijente koji se upotrebljavaju za izražavanje položaja rezultata, z vrijednosti imaju neke prednosti;
Z vrijednosti možemo zbrajati i dobivati prosjek – centile NE
Centili nisu ekvidistantne jedinice
Kod uporabe centila i decila nema smisla koristiti decimalna mjesta, uporaba z – vrijednosti omogućava korištenje više decimalnih mjesta (preporučljivo 2)
Prednost centila, decila – ne treba biti normalna raspodjela. Z vrijednosti su vezane za normalnu raspodjelu.
Z vrijednosti u R jeziku možemo napraviti na slijedeći način:
zproba_x <- (proba_x-mean(proba_x))/sd(proba_x)