Poglavlje 7 Obrada i prikaz neparametrije
Neparametrijska statistika koristi se kod podataka koji imaju neke od sljedećih karakteristika:
mali broj ispitanika ili nekih drugih entiteta u istraživanju (n<20 ili n<30, treba biti oprezan pri korištenju točnih brojeva jer navedene vrijednosti ovise o predmetu istraživanja i primijenjenoj metodologiji)
podaci su izraženi na nominalnim ili ordinalnim mjernim ljestvicama
raspodjela se značajno razlikuje od normalne (U-raspodjela, multimodalna raspodjela, Poissonova raspodjela)
Neke karakteristike korištenja neparametrijske statistike mogu se sažeti na slijedeći način:
Može se koristiti za sve vrste ljestvica
Jednostavan izračun
Ne traži populacijske podatke (nije i razina zaključivanja)
Rezultati mogu izgledati gotovo jednako kao i kod parametrijske statistike
U društvenim znanostima, pri ispitivanju stavova, ekstremne vrijednosti – često je obrnuta normalna raspodjela (U)
No, postoje i određena ograničenja u odnosu na druge procedure:
Sadrži nepotpune modele / podatke
Višestruke usporedbe – post hoc testovi
Snaga zaključivanja je manja od neparametrijskih testova
Snaga nekog testa odnosi se na vjerojatnost odbacivanja nul-hipoteze ako je ta hipoteza zaista pogrešna. Sposobnost otkrivanja razlike ako ta razlika zaista postoji.
U slijedećem tabličnom prikazu možemo vidjeti usporedbe između nekih svojstava neparametrijske i parametrijske statistike.
| parametrijski | neparametrijski | |
|---|---|---|
| intervalna, omjerna | ljestvica mjerenja | nominalna, ordinalna |
| normalna ili približno normalna | oblik raspodjele | nije relevantno |
| veća | statistička snaga | manja |
| podjednake | varijance | nije relevantno |
| veća | osjetljivost | manja |
| veća | razumljivost za korisnike | manja |
Kako provjeriti normalnost raspodjele dobivenih vrijednosti nekog istraživanja? Jedan od načina je prikaz raspodjele i odstupanje od normalne, zamišljene raspodjele. Drugi način je pomoću Q-Q prikaza.
Tako npr. u R sučelju možemo simulirati normalnu raspodjelu s N=100 te prikazati pomoću histograma i Q-Q slikovnog prikaza raspodjelu podataka.
normal.results <- rnorm (n=100)
hist(x=normal.results)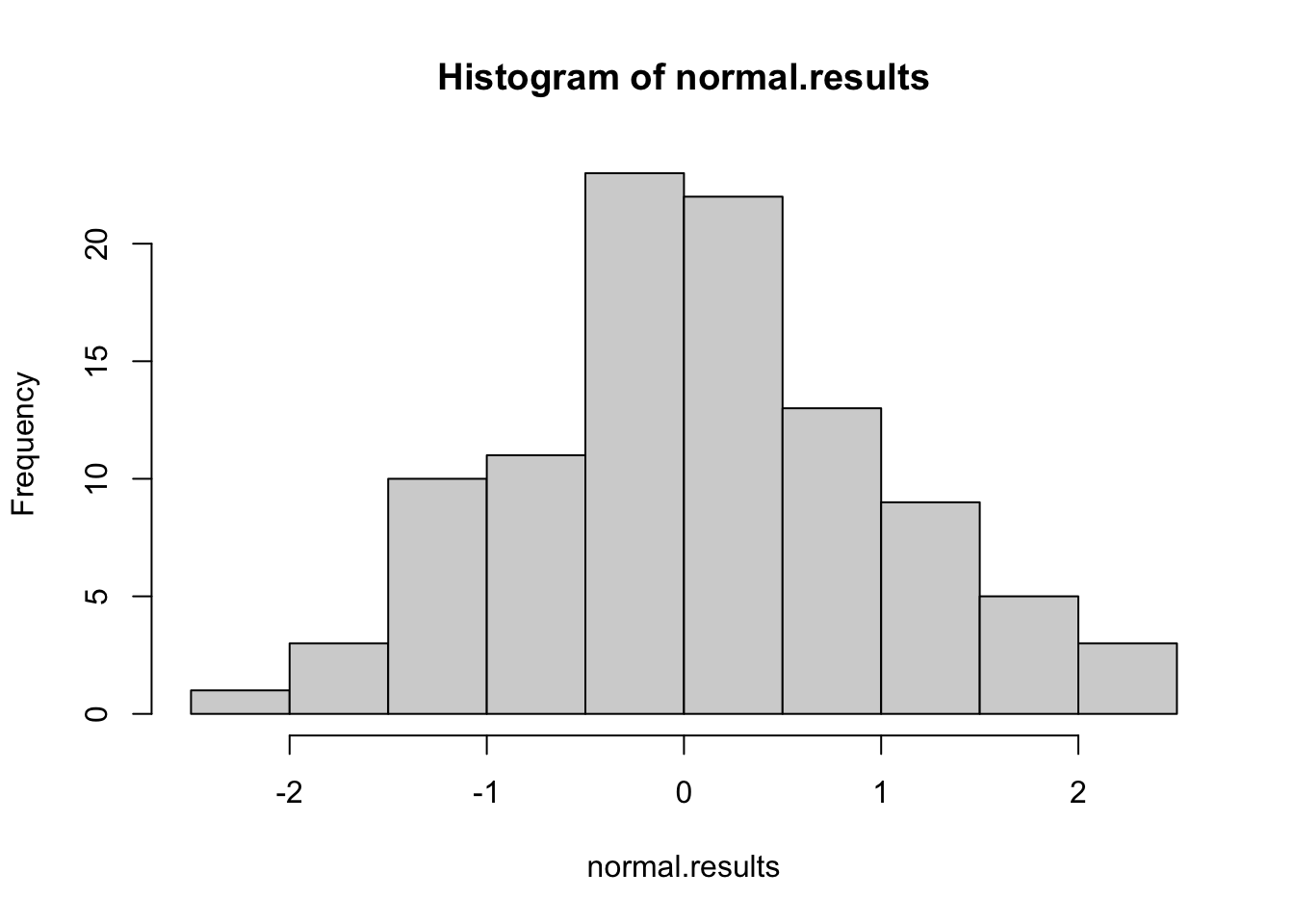
qqnorm(y=normal.results)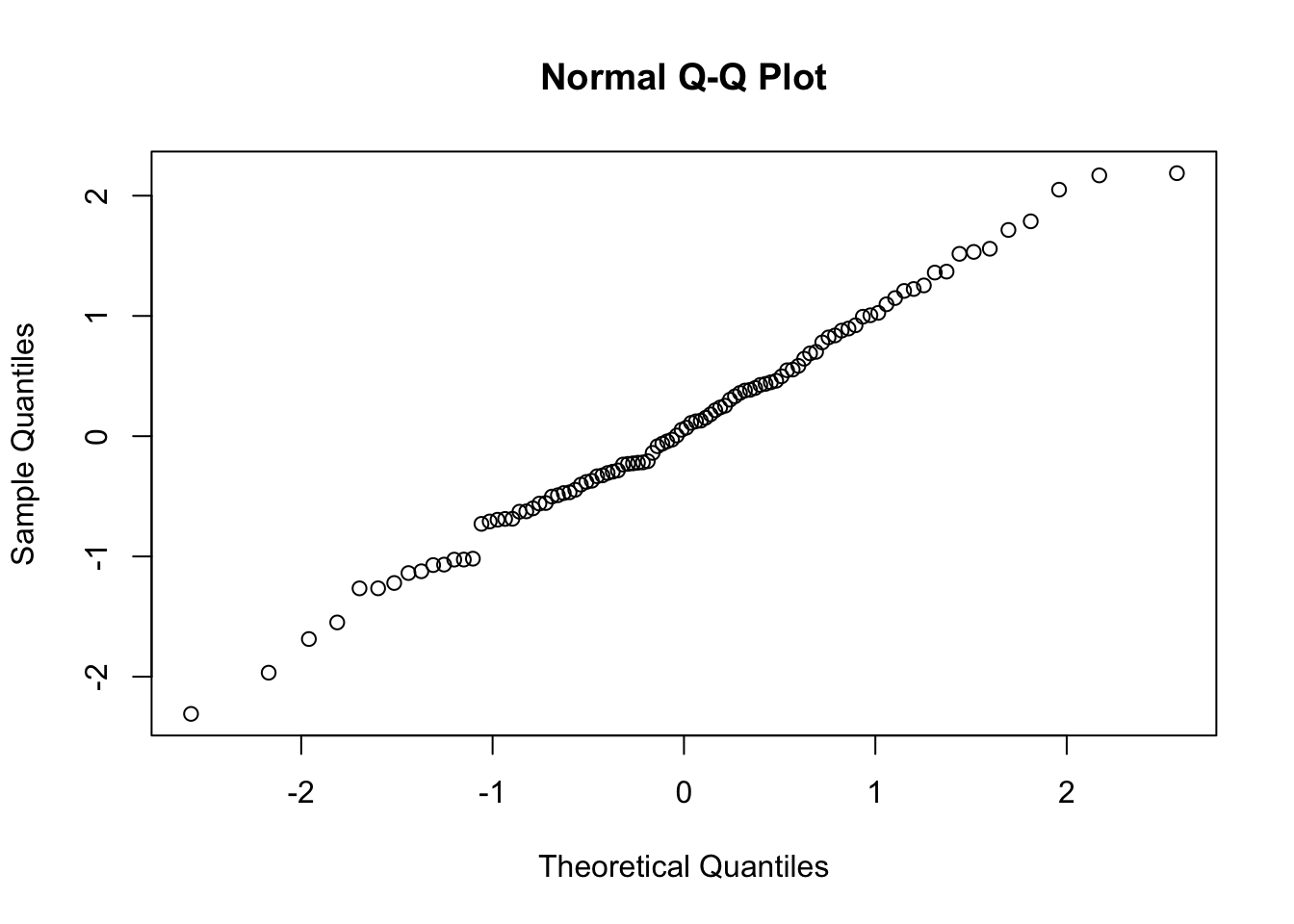
Ukoliko Q-Q slikovni prkaz prati zamišljnu linearnu liniju tada je dobivena raspodjela u okvirima normalne raspodjele.
Pomoću Shapiro-Wilk testa možemo numerički provjeriti da li navedena raspodjela podataka odstupa od normalne.
shapiro.test( x = normal.results )##
## Shapiro-Wilk normality test
##
## data: normal.results
## W = 0.99, p-value = 0.9Kako vidimo p vrijednost je veća od 0.05 te je statistički ne značajna razini od 95%.
7.1 Jedan uzorak - test hipoteze
Primjena neparametrijskog testa za jedan uzorak može se pronaći od znanosti do obrazovanja. Tako, primjerice želimo vidjeti da li je profesor ili ocjenjivač sklon davanju ocjena koje su različite od sredine tj. ocjene 3. Kako bi provjerili hipotezu, možemo se poslužiti primjerom slijedećih ocjena ocjenjivača Petra.
PodaciOcjene =("
Profesor Ocjena
'Petar' 3
'Petar' 4
'Petar' 5
'Petar' 4
'Petar' 4
'Petar' 5
'Petar' 5
'Petar' 3
'Petar' 2
'Petar' 5
")
PodaciOcjeneData = read.table(textConnection(PodaciOcjene),header=TRUE)
#PodaciOcjeneData$Ocjena = factor(PodaciOcjeneData$Ocjena,
# ordered = TRUE)
xtabs( ~ Profesor + Ocjena,
data = PodaciOcjeneData)## Ocjena
## Profesor 2 3 4 5
## Petar 1 2 3 4Navedeni primjer napravljen je prema uzoru poznatog paketa rcompanion te online knjige (S. S. Mangiafico, 2016).
U slijedećem koraku napravit ćemo križanje tablice (crosstabulation) koje pokazuje učestalosti i postotke.
xtabs( ~ Profesor + Ocjena,
data = PodaciOcjeneData)## Ocjena
## Profesor 2 3 4 5
## Petar 1 2 3 4#proporcija u slijedećem koraku
#prvo dodjelimo podatke varijabli i zatim prikažemo proporcije
proporcije = xtabs( ~ Profesor + Ocjena,
data = PodaciOcjeneData)
prop.table(proporcije,margin = 1)## Ocjena
## Profesor 2 3 4 5
## Petar 0.1 0.2 0.3 0.4Slikovni prikaz možemo napraviti također koristeći bazične barplot funkcije.
bar_ocjena = xtabs(~ Ocjena,
data=PodaciOcjeneData)
barplot(bar_ocjena,
col="dark gray",
xlab="Petar - ocjene",
ylab="Učestalost")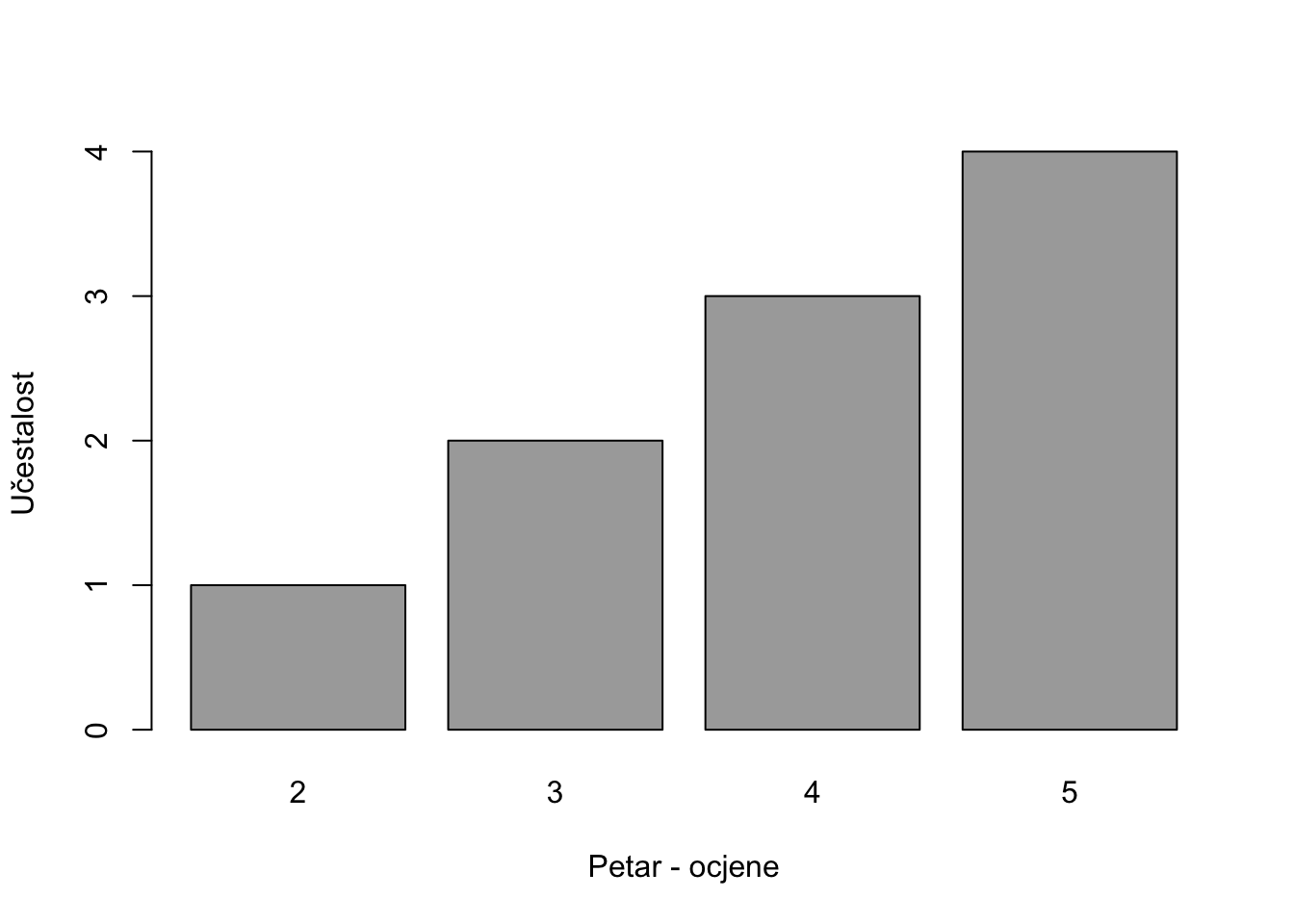
Iz slikovnog prikaza je vidljivo kako je raspodjela negativno asimetrična tj. veći broj vrijednosti ocjena je pomaknut prema vrijednosti 5. Deskriptivna statistika može se prikazati i pomoću FSA paketa na slijedeći način.
library(FSA)
Summarize(Ocjena ~ Profesor,
data=PodaciOcjeneData,
digits=3)## Profesor n mean sd min Q1 median Q3 max
## 1 Petar 10 4 1.054 2 3.25 4 5 5Vratimo se na početak primjera jer trebamo odgovoriti na pitanje da li je profesor ili ocjenjivač sklon davanju većih ocjena tj. trebamo ispitati razlikuju li se ocjenjivanje statistički značajno od 3? Za dobiti odgovor na to pitanje, osim slikovnog prikaza, potrebno je provesti test - Wilcoxon tekst predznaka (Wilcoxon signd-rank test).
Wilcoxon test pozivamo funkcijom wilcox.test gdje je u argumentima funkcije potrebno odrediti vrijednost mu tj. referentnu vrijednost od koje se određuje odstupanje distribucije ocjena. U našem primjeru to je vrijednost 3.
#prije primjene Wilcox testa - pretvaranje varijable u čistu numeričku varijablu
PodaciOcjeneData$Ocjena <- as.numeric(PodaciOcjeneData$Ocjena)
wilcox.test(PodaciOcjeneData$Ocjena,
mu=3,
conf.int=TRUE,
conf.level=0.95)##
## Wilcoxon signed rank test with continuity
## correction
##
## data: PodaciOcjeneData$Ocjena
## V = 34, p-value = 0.03
## alternative hypothesis: true location is not equal to 3
## 90 percent confidence interval:
## 3.5 5.0
## sample estimates:
## (pseudo)median
## 4.5Iz rezultata primjene Wilcoxon testa vidimo i raspon intervala pouzdanosti. Wilcoxon test je značajan na razini od 95%. Pomoću rcompanion paketa može se izračunati i efekt učinka za Wilcoxon test (S. Mangiafico, 2022).
library(rcompanion)
wilcoxonOneSampleR(PodaciOcjeneData$Ocjena,mu=3)## r
## 0.7057.2 Dva nezavisna uzorka
Dva vrlo često korištena testa za usporedbu dva nezavisna uzorka su medijan test i test sume rangova (Wilcoxon t test, Mann-Whitney U test).
Medijan test:
Svodi se na hi-kvadrat test
Izračunavanje centralne vrijednosti svih rezultata
Učestalost vrijednosti iznad i ispod medijana
Izračun hi-kvadrat testa
Test sume rangova (Wilcoxon t-test, Mann-Whitney U test) koristi drugačiju proceduru od medijan testa.
Koriste rangove - više informacija od medijan testa
Veća je snaga, snažniji test
Izračun Z vrijednosti iz sume rangova jednog i drugog uzorka (jer su dva nezavisna uzorka)
Wilcoxon test dolazi u dvije inačice, test za nezavisne uzorke (two sample Wilcoxon test) i za zavisne uzorke, kada je riječ o samo jednom uzorku ali u dva ponovljena mjerenja (one sample Wilcoxon test).
Dio neparametrijskih procedura ugrađen je u temeljni R paket stats. Tako, Wilcoxonov test sume rangova poziva se pomoću funkcije wilcox.test.
Zamislimo slijedeći istraživački primjer. U jednom natjecanju kušanja vina sudjelovali su Petar i Ivan koji su dobili slijedeće ocjene (od 1 do 5) od strane kušača.
UlazniPodaci =("
Vinar Likert
Petar 4
Petar 5
Petar 4
Petar 3
Petar 4
Petar 4
Petar 4
Petar 3
Petar 5
Petar 5
Ivan 2
Ivan 3
Ivan 2
Ivan 2
Ivan 1
Ivan 2
Ivan 3
Ivan 4
Ivan 2
Ivan 3
")
PodaciIvanPetar = read.table(textConnection(UlazniPodaci),header=TRUE) #Prebacivanje rezultata u tablicu
# Prebacivanje varijable Likert u factor
#PodaciIvanPetar$Likert = factor(PodaciIvanPetar$Likert, ordered = TRUE)
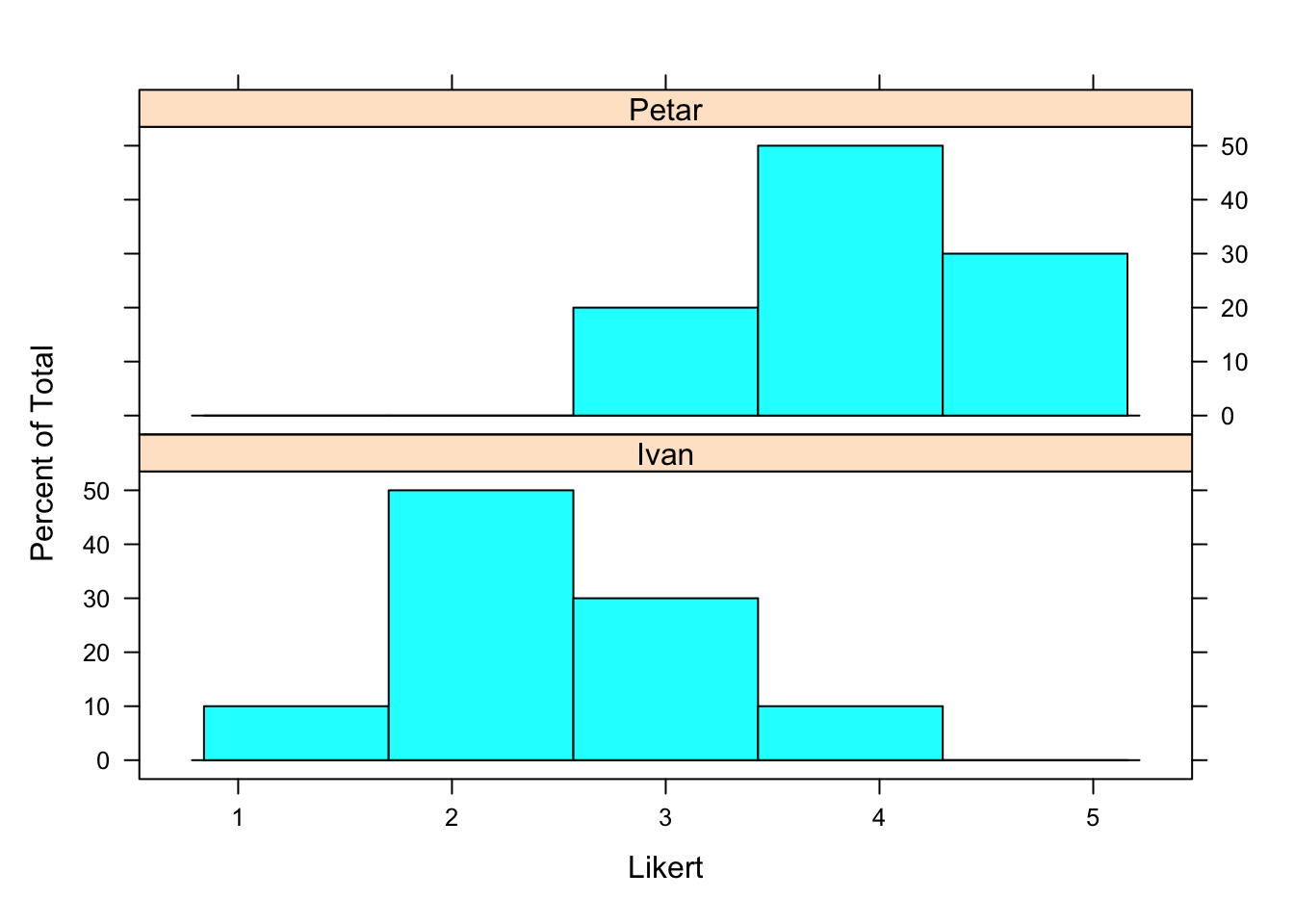
#PodaciIvanPetar$Vinar = factor(PodaciIvanPetar$Vinar)Pomoću paketa lattice (Sarkar, 2021) možemo prikazati raspodjelu vrijednosti za Petra i Ivana.
library(lattice)
histogram(~ Likert | Vinar,
data=PodaciIvanPetar,
layout=c(1,2) # columns and rows of individual plots
)
Primjer uporabe neparametrijske statistike može vidjeti koristeći neke od paketa u R-u koji imaju ugrađene funkcije za korištenje neparametrijskih procedura i to: BSDA (R-BSDA?), DescTools (Signorell, 2021).
Opisna statistika se jednostavno može prikazati pomoću paketa psych (Revelle, 2021).
library(psych)
describe.by(PodaciIvanPetar$Likert,PodaciIvanPetar$Vinar)##
## Descriptive statistics by group
## group: Ivan
## vars n mean sd median trimmed mad min max range
## X1 1 10 2.4 0.84 2 2.38 0.74 1 4 3
## skew kurtosis se
## X1 0.28 -0.84 0.27
## -----------------------------------------
## group: Petar
## vars n mean sd median trimmed mad min max range
## X1 1 10 4.1 0.74 4 4.12 0.74 3 5 2
## skew kurtosis se
## X1 -0.12 -1.35 0.23Primjena Wilcoxonovog testa za dva nezavisna uzorka u našem primjeru je vrlo jednostavna.
wilcox.test(formula = Likert ~ Vinar, data = PodaciIvanPetar)##
## Wilcoxon rank sum test with continuity
## correction
##
## data: Likert by Vinar
## W = 7.5, p-value = 0.001
## alternative hypothesis: true location shift is not equal to 0Rezultati primjene Wilcoxonovog testa pokazuju kako se procjene značajno razlikuju te kako Petar ima značajno veće vrijednosti tj. dobio je bolje ocjene za svoj proizvod od Ivana.
7.3 Jedan uzorak - dva mjerenja (zavisni test)
Kada imamo model u istraživanju jednog uzorka ali u dva ponovljena mjerenja, tada je test izbora Wilcoxonov test rangova (Wilcoxon Signed-Rank Test). Pozivanje testa je s istovjetnom funkcijom wilcox.test ali je potrebno uključiti opciju paired=TRUE.
Za demonstraciju primjene testa za zavisne uzorke, koristit ćemo primjer iz paketa MASS (Ripley, 2021) tj. podatke u datoteci immer. Ovaj primjer se odnosi na istraživanje prinosa žitarica u dvije godine (1931 i 1932) tako da prvo trebamo učitati paket MASS a zatim vidjeti zaglavlje datoteke immer.
library(MASS)
head(immer)## Loc Var Y1 Y2
## 1 UF M 81.0 80.7
## 2 UF S 105.4 82.3
## 3 UF V 119.7 80.4
## 4 UF T 109.7 87.2
## 5 UF P 98.3 84.2
## 6 W M 146.6 100.4Prije primjene Wilcoxonovog testa za zavisne uzorke, možemo prikazati slikovno raspodjelu vrijednosti i provjeru značajnosti odstupanja od normaliteta.
#slikovni prikaz raspodjele varijable Y1
hist(x=immer$Y1)
#opisna statistika za varijable Y1 i Y2
describe(immer$Y1)## vars n mean sd median trimmed mad min max
## X1 1 30 109 28.67 103 106.6 30.91 69.1 191.5
## range skew kurtosis se
## X1 122.4 0.79 0.15 5.24describe(immer$Y2)## vars n mean sd median trimmed mad min max
## X1 1 30 93.13 24.28 92.95 91.8 24.02 49.9 147.7
## range skew kurtosis se
## X1 97.8 0.37 -0.63 4.43#Provjera odstupanja od normaliteta
shapiro.test(x=immer$Y1)##
## Shapiro-Wilk normality test
##
## data: immer$Y1
## W = 0.93, p-value = 0.05Usporedba da li se značajno razlikuju dvije godine u prinosu žita pomoću wilcox.text funkcije. Obavezno uključena funkcija paired=TRUE.
wilcox.test(immer$Y1, immer$Y2, paired=TRUE) ##
## Wilcoxon signed rank test with continuity
## correction
##
## data: immer$Y1 and immer$Y2
## V = 368, p-value = 0.005
## alternative hypothesis: true location shift is not equal to 0Rezultati primjene neparametrijskog testa za zavisne uzorke pokazuju kako se prinos žita između dvije godine značajno razlikuje (p<0.01).
7.4 Tri i više nezavisnih uzoraka
Neparametrijska inačica analize varijance (ANOVA) koja se najčešće koristi u praksi je Kruskal-Wallis test. Ovaj test je ekstenzija Wilcoxonovog testa za nezavisne uzorke u situaciji kada imamo više od dva nezavisna uzorka a jednu zavisnu varijablu tj. predmet mjerenja.
Za simulaciju primjene K-W testa možemo upotrijebiti već dostupne podatke u sustavu tj. primjer PlantGrowth gdje su tri eksperimentalne manipulacije i vrijednosti rasta.
Pomoću funkcija provjeravamo zaglavlje datoteke i koliko razina ili skupina ima varijabla koja je u osnovi nezavisna varijabla u ovom modelu.
head(PlantGrowth)## weight group
## 1 4.17 ctrl
## 2 5.58 ctrl
## 3 5.18 ctrl
## 4 6.11 ctrl
## 5 4.50 ctrl
## 6 4.61 ctrllevels(PlantGrowth$group)## [1] "ctrl" "trt1" "trt2"Primjena Kruskal Wallis testa je jednostavna, pomoću funkcije kruskal.test.
kruskal.test(weight ~ group, data = PlantGrowth)##
## Kruskal-Wallis rank sum test
##
## data: weight by group
## Kruskal-Wallis chi-squared = 8, df = 2, p-value
## = 0.02Rezultati primjene K-W testa pokazuju kako se grupe značajno razlikuju na razini od 95% (p<0.05) ali ne znamo u kojem smjeru tj. nemamo informaciju između kojih skupina je statistički značajna razlika.
Za post-hoc test koristit ćemo funkciju pairwise.wilcox.test().
pairwise.wilcox.test(PlantGrowth$weight, PlantGrowth$group,
p.adjust.method = "BH")##
## Pairwise comparisons using Wilcoxon rank sum test with continuity correction
##
## data: PlantGrowth$weight and PlantGrowth$group
##
## ctrl trt1
## trt1 0.20 -
## trt2 0.09 0.03
##
## P value adjustment method: BHNakon primjene post-hoc testa vidimo da između grupa trt1 i trt2 postoji značajna razlika na razini od 95% (p<0.05).
7.5 Tri i više zavisnih uzoraka
Neparametrijska inačica analize varijance za zavisne uzorke je - Friedmanov test.
Nakon primjene Friedman testa, nemamo podatak između kojih mjerenja je razlika značajna. Za tu namjenu imamo dva rješenja, dva post hoc testa. Jedan je iz paketa PMCMR tj. Nemenyi Post-hoc test dok je drugi pomoću funkcije pairwiseSignTest iz rcompanion paketa.