Poglavlje 6 Obrada i prikaz kvantitativnih varijabli
Obrada rezultata kvantitativnih varijabli o kojima će ovdje biti riječi u analizama su u pravilu varijable koje pripadaju intervalnim i omjernim mjernim ljestvicama. Različita mjerenja provodimo na takvim varijablama. Naravno, gotovo uvijek u nekim područjima radimo isključivo s varijablama na intervalnoj mjernoj ljestvici. Varijable na omjernoj mjernoj ljestvici su jako rijetke, gotovo možemo reći zanemariva.
U većini istraživanja pokušavamo vidjeti razlike u takvoj varijabli između dviju skupina ispitanika. Tada je riječ o modelu razlika između dva nezavisna uzorka. Ukoliko imamo više nezavisnih ili zavisnih uzoraka, tada koristimo različite modele analize varijance. No, trebamo biti svjesni i preduvjeta za korištenje navedenih metoda a koje se odnose na normalitet raspodjele, veličinu uzorka, broj ponovljenih mjerenja ili nezavisnih uzoraka i sl. Parametrijski testovi su robusne metode za koje treba poznavati ograničenja jer se inače izlažemo riziku od donošenja pogrešnih zaključaka i izlažemo se nekoj od statističkih pogrešaka (tipa I ili II tj. alfa i beta pogreška).
Razumijevanje odnosa između parametrijske i neparametrijske statistike pretpostavlja znanje i metodologije istraživanja. Analize podataka a posebice one koje se odnose na populaciju i zaključivanje o populaciji, zahtijevaju permanentno promišljanje o pogrešci mjerenja kojoj se izlažemo.
6.1 Standardna pogreška i interval pouzdanosti
Za pravilnu uporabu t-testa a i drugih statističkih testova, potrebno je dobro razumijevanje odnosa između uzorka i populacije tj. razumijevanje koncepta pogreške mjerenja pogreške koja se veže uz pojedinačnu aritmetičku sredinu i standardnu devijaciju ali i pogreške koja se veže uz razliku između dviju aritmetičkih sredina tj. standardna pogreška razlike između dvije aritmetičke sredine.
Iz vrijednosti standardne pogreške i njenog razumijevanja proizlazi izračunavanje intervala pouzdanosti (eng. confidence interval) koji se izražava na razini od 95 ili 99%. Interval pouzdanosti je statistika koja nam predstavlja raspon unutar kojega se uz određenu vjerojatnost nalazi tražena statistička mjera (aritmetička sredina populacije, standardna devijacija populacije i sl.). Razumijevanja intervala pouzdanosti važno je i kod analize složenijih statističkih postupaka poput linearne regresijske analize i drugih multivarijatnih metoda.
Populaciju čine sve jedinke ili entiteti koji imaju neko zajedničko svojstvo ili svojstva. Uzorak je dio populacije koji može imati različite karakteristike i određeni stupanj reprezentativnosti.
Uzorak je uvijek procjena populacije i uvijek se uz njega veže određena pogreška. Aritmetička sredina uzorka uvijek je procjena i odstupa u određenoj mjeri od prave (populacijske, označava se s \(\mu\)) aritmetičke sredine.
Prilikom uzimanja slučajnih uzoraka trebamo uzeti u obzir i slučajne varijacije svojstava predmeta mjerenja među uzorcima. Naravno, što je veći varijabilitet ili raspršenje to će biti i veći varijabilitet među uzorcima.
Standardna devijacija aritmetičkih sredina uzoraka je manja što je uzorak veći. Jednako tako, što je uzorak veći to smo bliži procjeni prave aritmetičke sredine tj. aritmetička sredina uzorka bliža je pravoj aritmetičkoj sredini.
Raspodjela aritmetičkih sredina ići će prema obliku normalne raspodjele, čak i onda kada predmet mjerenje iz populacije nije normalno raspodjeljen. Tu pojavu nazivamo teorem centralne granice.
(Petz et al., 2012) navodi i najkraću definiciju navedenog teorema - distribucija aritmetičkih sredina uzoraka približava se normalnoj kako N uzorka raste.
Iz prethodnog vrijedi, što je uzorak veći i varijabilnost pojave u populaciji manja, to je procjena parametara populacije iz uzorka točnija.
Statistički pokazatelj koji je u ovoj raspravi jako važan jest standardna pogreška aritmetičke sredine a koja služi u procjeni odstupanja aritmetičke sredine uzorka od prave aritmetičke sredine. Formula za izračunavanje uzima u obzir upravo navedeno: varijabilitet i veličinu uzorka.
\[\begin{equation}\label{pogreška aritmetičke sredine} SD_{\overline{x}}=\frac{SD}{\sqrt{N}} \end{equation}\]
U slijedećem prikazu nalazi se formula za izračunavanje standardne pogreške između dvije aritmetičke sredine. Ona je u osnovi zbroj pogrešaka koje se ‘vežu’ uz jednu i drugu aritmetičku sredinu. Pravilno razumijevanje standardne pogreške razlike između dvije aritmetičke sredine podrazumijeva simulaciju većeg broj uzorkovanja i većeg broj izračuna vrijednosti standardnih pogrešaka između dvije aritmetičke sredine. Prema tome, treba zamisliti i raspodjelu tih vrijednosti.
\[\begin{equation}\label{pogreška razlika između aritmetičkih sredina} SD_{M_{1}-M_{2}}=\sqrt{SD^{2}_{M_{1}}+SD^{2}_{M_{2}}} \end{equation}\]
Pri korištenju statističkih testova, izračuna p vrijednosti te interpretacije iste, moramo voditi računa o pogrešci. Tako, u statističkom zaključivanju poznate su dvije pogreške, \(\alpha\) (alfa) pogreška i \(\beta\) (beta) pogreška.
Pokušajmo vidjeti kako izgleda simulacija u R jeziku odnosa između uzorka i populacije u pojmovima standardne pogreške i intervala pouzdanosti.
Pretpostavimo uzorkovanje 100 puta veličine 10 ispitanika s aritmetičkom sredinom 100 i devijacijom 5. Takav uzorak pridjelit ćemo objektu uzorak1 te sintaksa izgleda na slijedeći način:
uzorak1 <- replicate(100, rnorm(10, mean = 100, sd = 5))Sada ćemo izračunati aritmetičku sredinu uzoraka. Dakle, imamo 10 uzoraka.
xbar <- apply(uzorak1, 2, mean)Raspodjela aritmetičkih sredina svih uzoraka izgleda ovako:
hist(xbar, nclass = 20, col = "grey", xlab = "Aritmetičke sredine uzoraka veličine 10", main = "Aritmetičke sredine uzoraka", xlim = c(90, 110))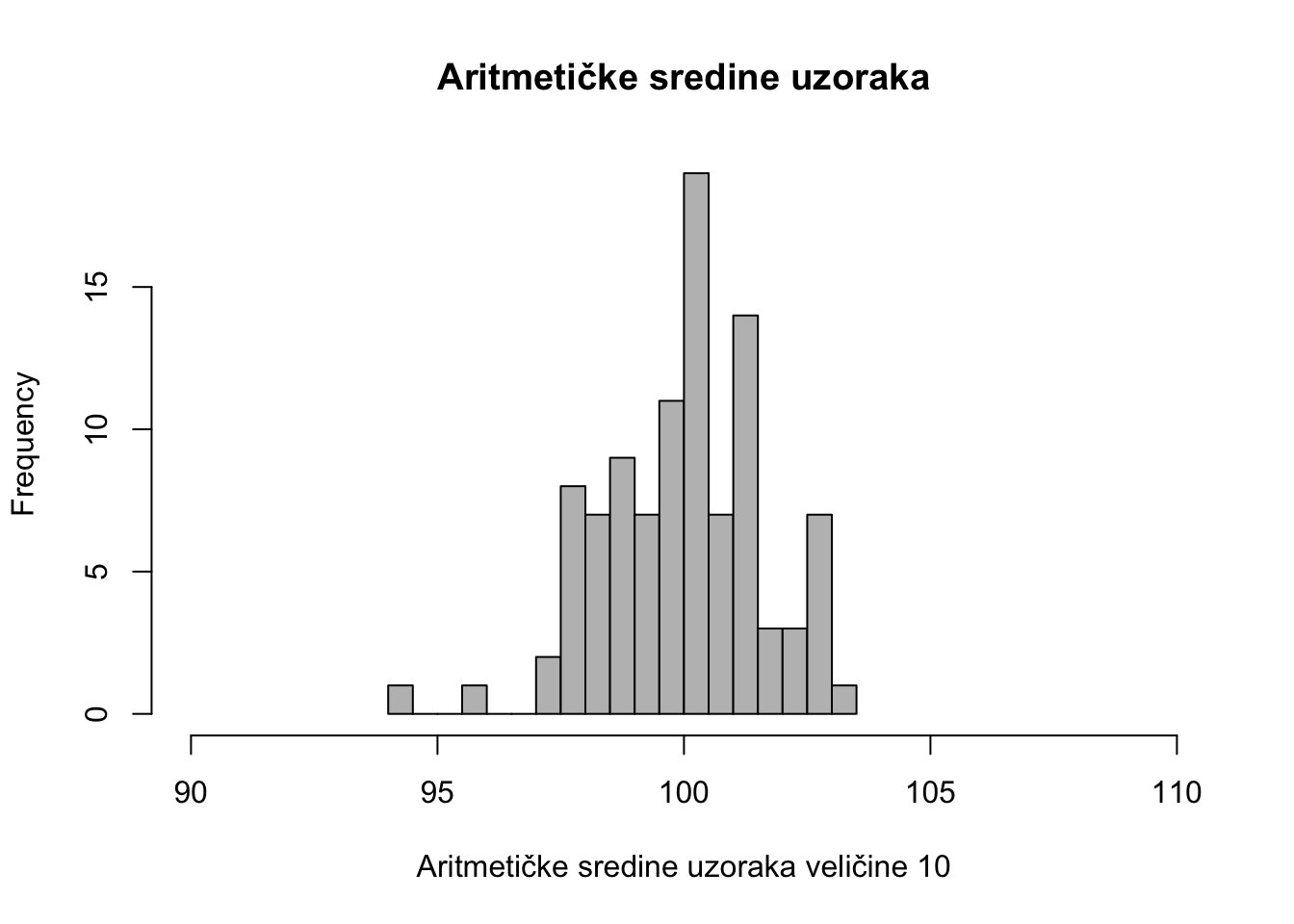
Kao što vidimo aritmetičke sredine uzoraka također opisuju normalnu raspodjelu. Ova pojava je poznata i kao teorem centralne granice.
6.2 Jednostavni t-test ili t-test na jednom uzorku
Jednostavni t-test je provedba t-testa na jednom uzorku gdje se analizira odstupanje aritmetičke sredine uzorka od zamišljene ili hipotetske aritmetičke sredine populacije (\(mu\)). Pretpostavimo mjerenje tjelesne težine na 100 ispitanika koji su postigli aritmetičku sredinu od 80 kg i standardnu devijaciju od 10kg.
uzorak_tezina_1 <- c(rnorm(100, mean = 80, sd = 10))Ukoliko želimo provjeriti da li navedeni uzorak statistički značajno odstupa od hipotetske vrijednosti od 90.
t.test(uzorak_tezina_1, mu = 90) # Ho: mu = 90##
## One Sample t-test
##
## data: uzorak_tezina_1
## t = -11, df = 99, p-value <0.0000000000000002
## alternative hypothesis: true mean is not equal to 90
## 95 percent confidence interval:
## 76.42 80.50
## sample estimates:
## mean of x
## 78.466.3 Analiza razlika imeđu dva uzorka (T - test)
T test je nastao 1908. zahvaljujući kemičaru William Sealy Gossetu koji je radio pod pseudonimom “A Student” u poznatoj pivovari koja proizvodi čuveno pivo Guinness (Boland, 1984).
Gosset je bio zaposlen kao kemičar te je u praksi imao problem s kušanjem određene količine piva te je imao potrebu razviti test, temeljem kojeg će moći iz manjih uzoraka piva procijeniti populaciju. Populacija u tom slučaju je cjelokupno pivo iz koje je izvučen uzorak piva. Upotrebu t-testa, Gosset je objavio u časopisu Biometrika pod pseudonimom Student jer je to bio zahtjev tvrtke Guinness koja nije željela da konkurencija zna što sve rade u svojim pogonima.
T test pripada parametrijskim testovima ili parametrijskoj statistici. Razlika između parametrijskih i neparametrijskih testova ogleda se u više svojstava a neka od njih su veličina uzorka, mjerna ljestvica, zaključivanje na razini populacije, odstupanje od normalne raspodjele i dr. Parametrijski testovi rabe se na većim uzorcima, intervalnoj ili omjernoj mjernoj ljestvici te je u pravilu zaključivanje o populaciji iz parametara uzorka čiji rezultati ne odstupaju od normalne raspodjele.
Neparametrijski testovi su upravo suprotno tj. koriste se na manjim uzorcima (N<20), na varijablama koje su na nominalnoj ili ordinalnoj mjernoj ljestvici te nas u pravilu ne zanima odnos između uzorka i populacije tj. zaključivanje (generalizacija) na populacijskoj razini. Pri primjeni neparametrijskih testova nije važno koliko raspodjela odstupa od normalne ili koliko je i u kojem smjeru izražena asimetričnost raspodjele.
T test za nezavisne uzorke koristi se u modelu podataka kada želimo dvije različite skupine ispitanika (ili uzoraka) usporediti u nekoj varijabli koja je kvantiativna, kontinuirana. (u pravilu na intervalnoj ili omjernoj mjernoj ljestvici).
Opći model sintakse za primjenu t-testa za nezavisne uzorke je: t.test(y~x) tj. y varijabla je kontinuirana varijabla, dok je x varijabla grupirajuća varijabla ili nezavisna varijabla. U grupirajućoj, nezavisnoj varijabli su određene vrijednosti ili kodovi koji označavaju dva nezavisna uzorka. No, treba biti oprezan, jer kada je riječ o dvije nezavisne varijable koje su tako i unesene u datoteku, tada je sintaksa t.test(x,y)
Jedna od pretpostavki za korištenje t testa za nezavisne uzorke je i jednakost varijanci. Pretpostavka uporabe t-testa je usporedba dva uzorka koji dolaze iz iste populacije. Nul hipoteza u tom slučaju je - dvije aritmetičke sredine su jednake a alternativna hipoteza kako te dvije aritmetičke sredine nisu jednake.
U praksi se mogu koristiti dvije inačice t - testa: 1) Student t-test 2) Welch t-test. Razlika između dva navedena je što se Welch t-test koristi kada varijance nisu jednake.
Provjeru jednakosti varijance između dva uzorka u R-u možemo napraviti vrlo jednostavno pomoću funkcije var.test.
prvi_uzorak <- rnorm(100,mean=100, sd=10)
drugi_uzorak <- rnorm(200,mean=100,sd=15)
var.test(prvi_uzorak,drugi_uzorak)##
## F test to compare two variances
##
## data: prvi_uzorak and drugi_uzorak
## F = 0.46, num df = 99, denom df = 199, p-value =
## 0.00002
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.3295 0.6536
## sample estimates:
## ratio of variances
## 0.4595Iz navedenog primjera vidljiv je značajan F test (p<0.01) i varijance nisu jednake.
Ako varijance nisu jednake, tada trebamo u općoj formuli ili funkciji t.test napisati i argument var.equal = FALSE.
# Opća formula za t-test za nezavisne uzorke
# t.test(x, y, alternative = "two.sided", var.equal = FALSE)
#Primjer: usporedba broja bodova koji su postigli studenti i studentice
#dva nezavisna uzorka
studenti_brb <- c(38,41,52,54,57,45,39,34,39,45,66,56,38,56,45)
studentice_brb <- c(56,78,48,38,39,44,56,58,34,78,69,89,68,89,78)
#primjena t-test za nezavisne uzorke
t.test(studentice_brb,studenti_brb, alternative = "two.sided",var.equal = FALSE)##
## Welch Two Sample t-test
##
## data: studentice_brb and studenti_brb
## t = 2.7, df = 21, p-value = 0.01
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 3.33 25.60
## sample estimates:
## mean of x mean of y
## 61.47 47.00Navedene varijable moguće je prebaciti u format data frame tj. retci ispitanici a stupci varijable. To je moguće pomoću funkcije data.frame.
test_bodovi <- data.frame(
skupina = rep(c("Studentice", "Studenti"), each = 15),
bodovi = c(studentice_brb, studenti_brb)
)
#prikaz rezultata
print(test_bodovi)## skupina bodovi
## 1 Studentice 56
## 2 Studentice 78
## 3 Studentice 48
## 4 Studentice 38
## 5 Studentice 39
## 6 Studentice 44
## 7 Studentice 56
## 8 Studentice 58
## 9 Studentice 34
## 10 Studentice 78
## 11 Studentice 69
## 12 Studentice 89
## 13 Studentice 68
## 14 Studentice 89
## 15 Studentice 78
## 16 Studenti 38
## 17 Studenti 41
## 18 Studenti 52
## 19 Studenti 54
## 20 Studenti 57
## 21 Studenti 45
## 22 Studenti 39
## 23 Studenti 34
## 24 Studenti 39
## 25 Studenti 45
## 26 Studenti 66
## 27 Studenti 56
## 28 Studenti 38
## 29 Studenti 56
## 30 Studenti 45Vizualizacija razlika između skupina moguće je na više načina. Najjednostavniji način je pomoću funkcije boxplot.
boxplot(mpg~cyl,data=mtcars, main="Automobili - potrošnja",
xlab="Number of Cylinders", ylab="Miles Per Gallon")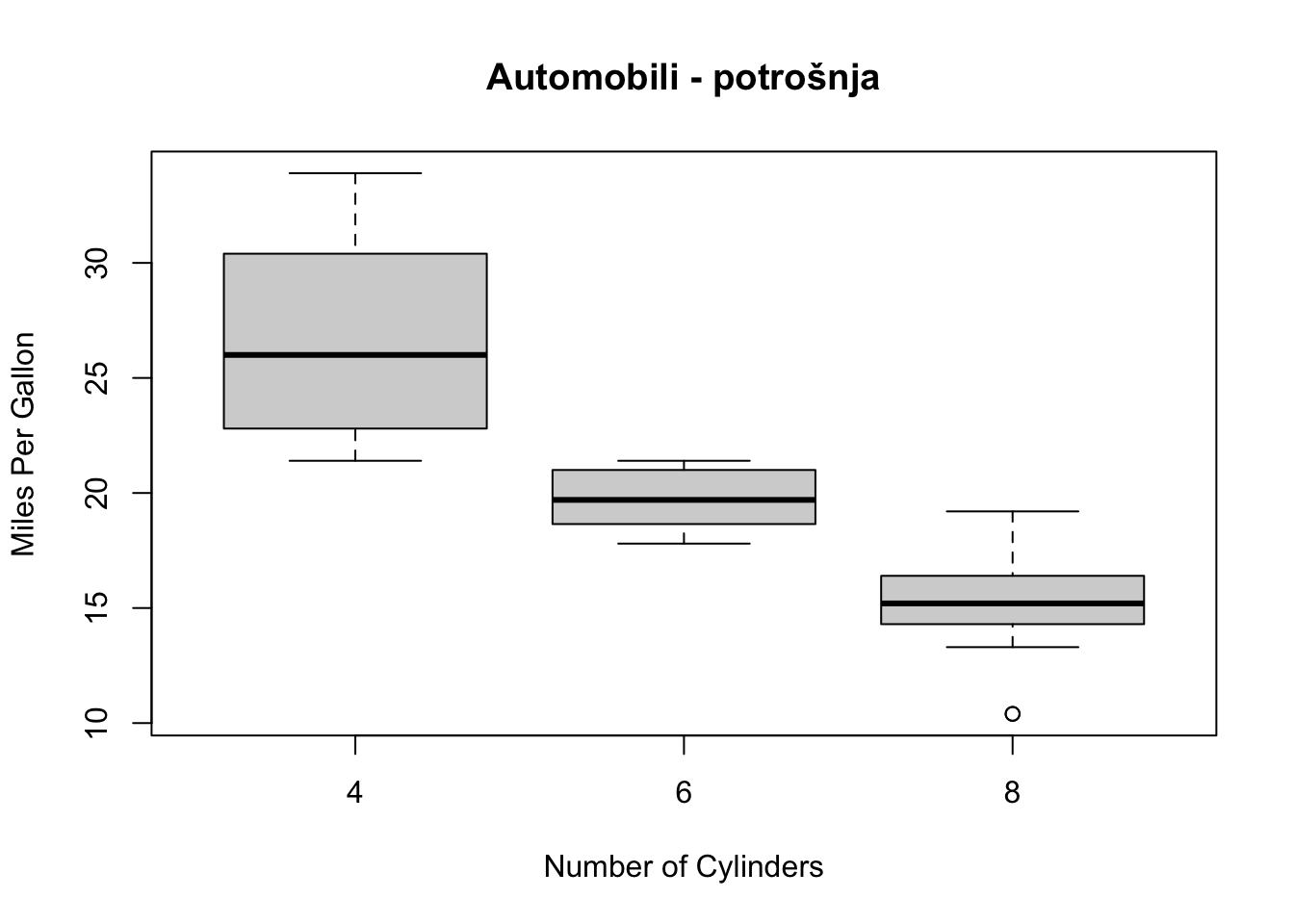
Vizualizacija rezultata pomoću paketa ggpubr koji omogućava prilagođene slikovne prikaze za potrebe znanstvenih publikacija.
library("ggpubr")
ggboxplot(test_bodovi, x = "skupina", y = "bodovi",
color = "skupina", palette = c("#00AFBB", "#E7B800"),
ylab = "Bodovi", xlab = "Skupina")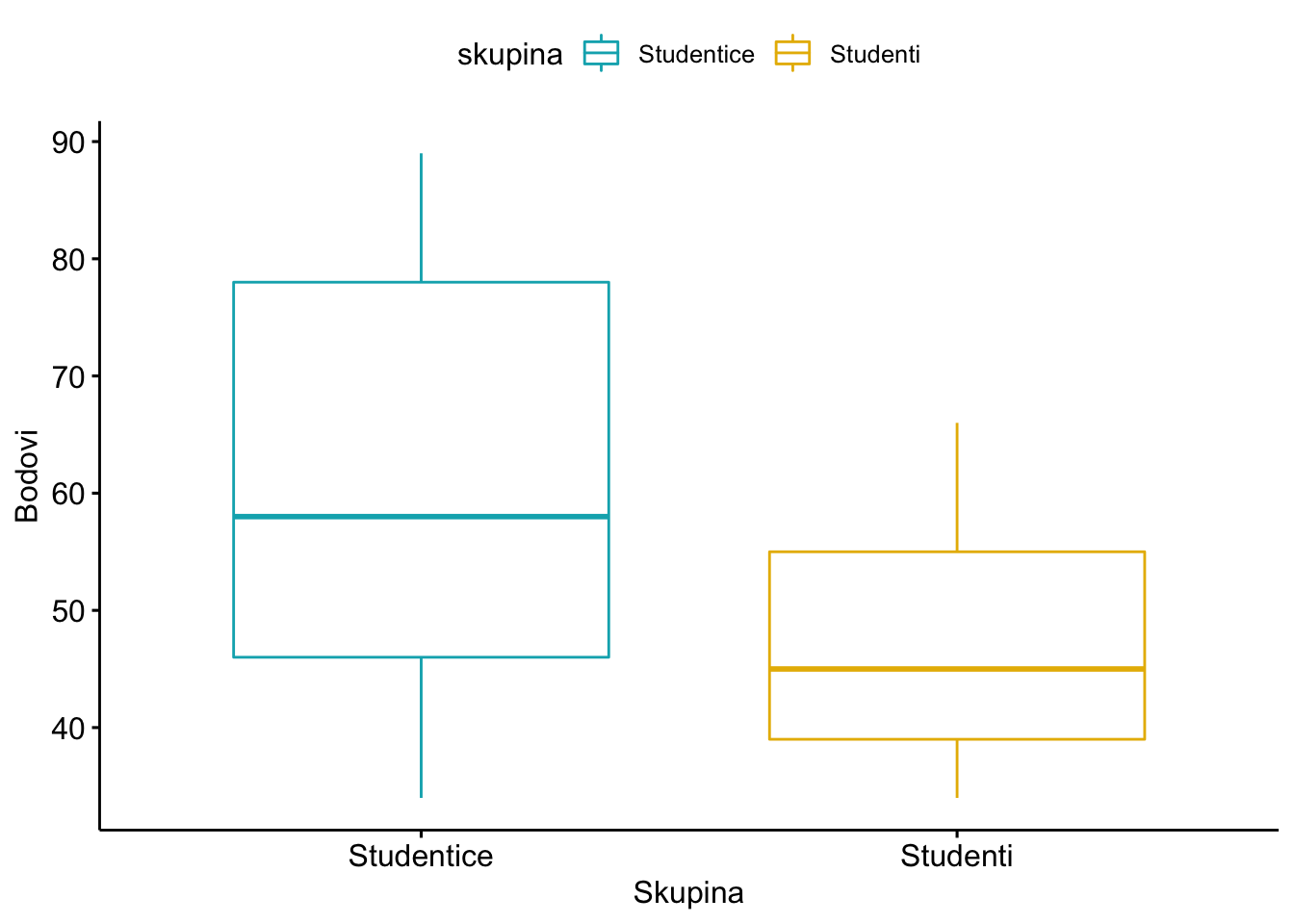
6.3.1 Zavisni uzorci
Dva zavisna uzorka ili ponovljeno mjerenje na istom uzorku ispitanika najčešće se testiraju pomoću t-testa za zavisne uzorke (paired t-test). Opća formula za izračunavanje t testa za zavisne uzorke glasi na slijedeći način.
#t.test(y1,y2,paired=TRUE) # where y1 & y2 are numeric Uzmimo primjer testiranja lijeka za hipertenziju. Utvrdili smo na 1000 ispitanika tlak od prosječno 155 mmHg a nakon primjene testnog lijeka tlak se na istih 1000 ispitanika spustio na prosječno 145 mmHg. U prvom mjerenju standardna devijacija bila je 12 mmHg a u drugom mjerenju 10 mmHg. Postavlja se pitanje da li je prosječno tlak statistički značajno manji u drugom mjerenju nakon primjene novog lijeka?
prije_lijeka <- c(rnorm(1000, mean = 155, sd = 12))
poslije_lijeka <- c(rnorm(1000, mean = 145, sd = 10))
t.test(prije_lijeka,poslije_lijeka,paired = TRUE)##
## Paired t-test
##
## data: prije_lijeka and poslije_lijeka
## t = 21, df = 999, p-value <0.0000000000000002
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 8.843 10.695
## sample estimates:
## mean of the differences
## 9.769Pogledajmo dalje na još jednom primjeru. Možemo uzeti primjer mjerenja tjelesne težine deset ispitanika prije i poslije tretmana dijete.
# Mjere tjelesne težine unesemo u dva vektora
tt_prije <- c(93,95,88,102,98,110,89,92,97,115)
tt_poslije <- c(85,88,80,90,92,99,83,85,90,105)
#navedena dva vektora prebacimo u oblik okvira s podacima
tezina_frame <- data.frame(
skupina = rep(c("prije", "poslije"), each = 10),
tezina = c(tt_prije, tt_poslije)
)
#provjera kako izgleda okvir s podacima (data.frame) ili matrica s podacima u dvije varijable i 10 ispitanika
print(tezina_frame)## skupina tezina
## 1 prije 93
## 2 prije 95
## 3 prije 88
## 4 prije 102
## 5 prije 98
## 6 prije 110
## 7 prije 89
## 8 prije 92
## 9 prije 97
## 10 prije 115
## 11 poslije 85
## 12 poslije 88
## 13 poslije 80
## 14 poslije 90
## 15 poslije 92
## 16 poslije 99
## 17 poslije 83
## 18 poslije 85
## 19 poslije 90
## 20 poslije 105Deskriptivnu statistiku možemo dobiti na više načina a za potrebe t-testa ovdje ćemo demonstrirati dva paketa: pych i dplyr.
Pomoću psych paketa možemo jednostavno dobiti opisnu statistiku prema dva ponovljena mjerenja.
library(psych)
describeBy(tezina_frame$tezina, group = tezina_frame$skupina)##
## Descriptive statistics by group
## group: poslije
## vars n mean sd median trimmed mad min max range
## X1 1 10 89.7 7.54 89 89 5.93 80 105 25
## skew kurtosis se
## X1 0.69 -0.71 2.39
## -----------------------------------------
## group: prije
## vars n mean sd median trimmed mad min max range
## X1 1 10 97.9 8.82 96 97 7.41 88 115 27
## skew kurtosis se
## X1 0.7 -0.94 2.79Sličan prikaz možemo dobiti pomoću dplyr paketa.
library(dplyr)
group_by(tezina_frame,skupina) %>%
summarise(
count = n(),
mean = mean(tezina, na.rm = TRUE),
sd = sd(tezina, na.rm = TRUE)
)## # A tibble: 2 × 4
## skupina count mean sd
## <chr> <int> <dbl> <dbl>
## 1 poslije 10 89.7 7.54
## 2 prije 10 97.9 8.82Slično kao i u primjeru t testa za nezavisne uzorke, možemo napraviti pomoću ggpubr paketa i slikovni prikaz:
library(ggpubr)
ggboxplot(tezina_frame, x = "skupina", y = "tezina",
color = "skupina", palette = c("#00AFBB", "#E7B800"),
order = c("prije", "poslije"),
ylab = "Tjelesna težina (kg)", xlab = "Skupina")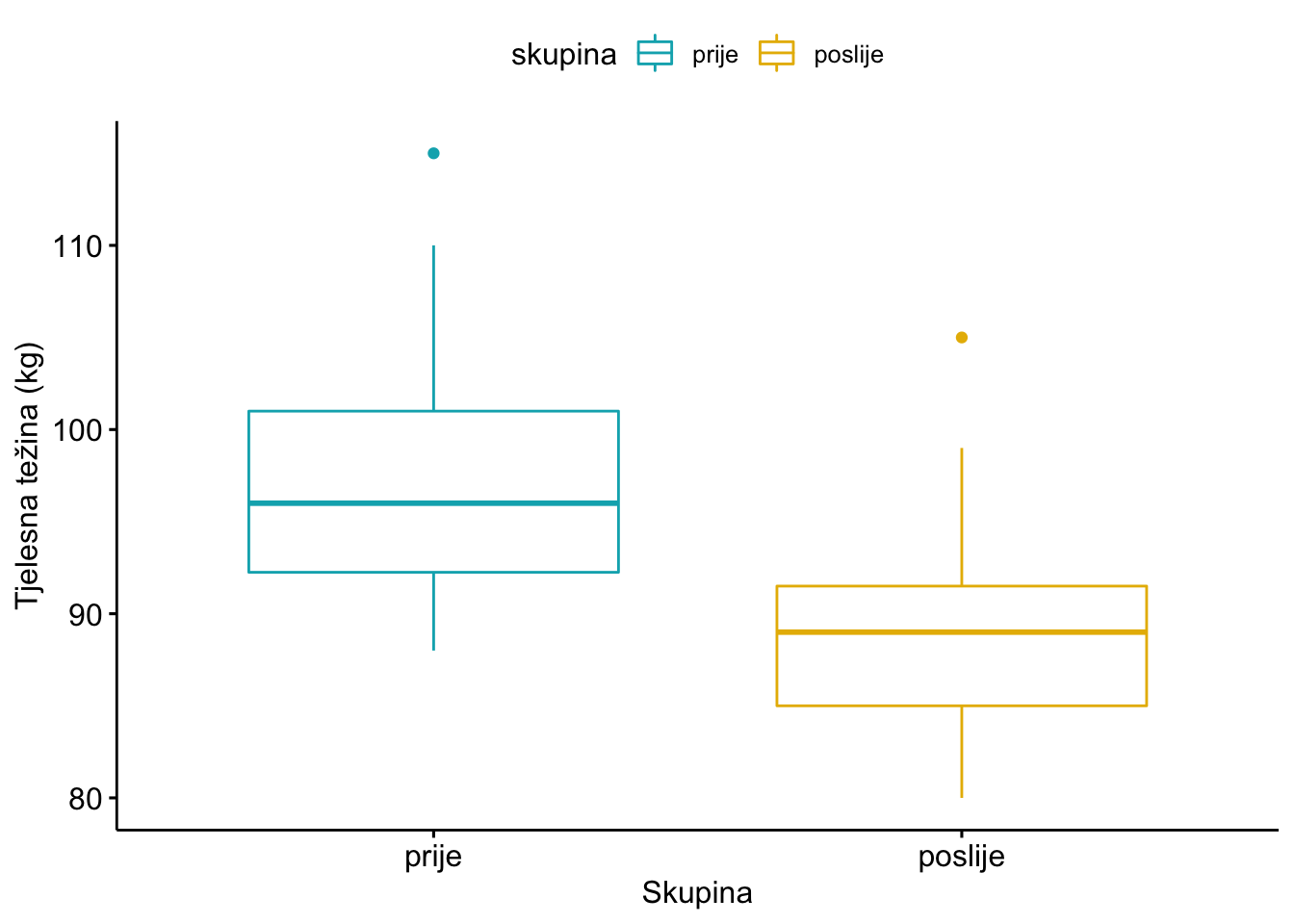
Konačno, pitanje da li je navedena razlika u prosječnim vrijednostima koju vidimo na slikovnom prikazu a i u prethodnom tabličnom prikazu statistički značajna ili ne, trebamo primijeniti t test za zavisne uzorke.
ttest_tezine <- t.test(tt_prije,tt_poslije,paired = TRUE)
ttest_tezine##
## Paired t-test
##
## data: tt_prije and tt_poslije
## t = 12, df = 9, p-value = 0.0000006
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 6.699 9.701
## sample estimates:
## mean of the differences
## 8.2Iz rezultata primjene t testa za zavisne uzorke, razvidno je kako je p vrijednost (p = 5.975e-07) značajna na razini od 99% (p<0.01). T vrijednost je 12.362.
No, prije primjene t testa, poglavito kada se radi o malim uzorcima kao što je ovaj gdje je N<30, treba primjeniti test za provjeru odstupanja navedenih varijabli od normalne raspodjele. Za to se koristi Shapiro-Wilk test. Kako bi to proveli, potrebno je izračunati razliku između težina prvog i drugog mjerenja i na takvoj varijabli provesti Shapiro Wilk test.
d_tezina <- with(tezina_frame,
tezina[skupina == "prije"] - tezina[skupina == "poslije"])
shapiro.test(d_tezina)##
## Shapiro-Wilk normality test
##
## data: d_tezina
## W = 0.88, p-value = 0.1Rezultat primjene Shapiro Wilk testa pokazuje kako test nije značajan na razini od 95% (p>0.05) i kako opravdano možemo zaključiti kako varijabla razlika između prvog i drugog mjerenja ne odstupa značajno od normalne raspodjele.
6.4 Analiza varijance (ANOVA)
Začetci analize varijance vežu se uz ime Sir Ronald Aylmer Fisher (1890-1962) koji je bio statističar, genetičar i evolucijski biolog te začetnik neodarvinističke sinteze (neo-Darwinian synthesis) i promotor eugenike (The Genetical Theory) (Fisher, 1919). Za njega mnogi smatraju kako je najveće ime nakon Darwina a takvom izjavom se posebno ističe Richard Dawkins (“the greatest biologist since Darwin”) i A. Hald (“a genius who almost single-handedly created the foundations for modern statistical science”).
6.4.1 Zašto ANOVA?
Analiza varijance je statistički postupak kojim se uspoređuju različite komponente varijance (kvadrirane standardne devijacije).
Jednostavna analiza varijance primjenjuje se kada uspoređujemo rezultate jedne zavisne varijable unutar jedne nezavisne varijablom koja ime više razina ili kategorija. Primjer je istraživanje da li između četiri dobne skupine ispitanika (1: 10-19 godina, 2: 20-29, 3: 30-49, 4: 50-59) postoji statistički značajna razlika u razini kolesterola u krvi. U ovom slučaju možemo primijeniti postupak jednostavne analize varijance jer želimo vidjeti da li između većeg broja dobnih skupina (nezavisna varijabla) postoji statistički značajna razlika u razini kolesterola u krvi (zavisna varijabla).
Složena analiza varijance je statistički postupak koji se primjenjuje u onim slučajevima kada uspoređujemo rezultate više zavisnih varijabli unutar više nezavisnih varijabli koje imaju različite razine ili kategorije. Za razliku od jednostavne analize varijance, gdje imamo samo jednu zavisnu varijablu, kod složene analize varijance, osim utjecaja većeg broja nezavisnih varijabli na zavisnu, gledamo i međudjelovanje (interakciju) između većeg broja zavisnih varijabli.
Dakle, u slučaju jednostavne analizu varijance, kada želimo utvrditi kako neka nezavisna varijabla utječe na neku zavisnu varijablu potrebno je imati: a) veći broj kategorija nezavisne varijable b) za svaku od kategorija određeni broj ispitanika na kojima su prikupljeni podaci o zavisnoj varijabli c) zavisnu varijablu koja je metrička, kontinuirana varijabla
Općenito logika jednostavne analize varijance počiva na: a) odstupanjima pojedinačnih rezultata od vlastite aritmetičke sredine, i tu imamo variranje unutar skupine kojoj pripada ispitanik i na: b) odstupanjima aritmetičkih sredina pojedinih skupina rezultata od zajedničke aritmetičke sredine svih rezultata
Dakle, za analizu varijance važan je odnos varijance između i unutar skupina. Izračunava se tzv. F-vrijednost testa:
\[\begin{equation}\label{F omjer} F=\frac{V_{ig}}{V_{ug}} \end{equation}\]
Iz formule je vidljivo da što je veće variranje rezultata između skupina ispitanika u odnosu na variranje unutar skupina, to je F omjer veći. Što je veći F-omjer, uz pripadajuće stupnjeve slobode, to je i opravdanije odbacivanje nul-hipoteze.
Na sljedećem slikovnom prikazu je jedan od primjera raspodjele rezultata zavisne varijable (npr. koncentracije leukocita) za četiri kategorije nezavisne varijable kada se rezultati značajno preklapaju.
SLIKA - različite distribucije i preklapanje
Iz slike je vidljivo značajno preklapanje rezultata pojedinih skupina jer je varijabilitet između skupina (Vis) manji od varijabiliteta unutar skupina (Vus). Na sljedećoj je slici vidljiva obrnuta situacija: jasna razlika između skupina očituje se zbog većeg varijabiliteta između skupina (Vis) u odnosu na varijabilitet unutar skupina (Vus).
SLIKA - nema preklapanja raspodjela
Osnovna mjera koju dobijemo nakon provedene analize varijance je omjer varijance među skupinama i varijance unutar skupina. Slično smo imali i kod t-testa. U svakom slučaju logika je ista: dobije se određena vrijednost F-omjera, pripadajući stupnjevi slobode (df) i p-vrijednost (koja se tumači na isti način kao i kod svih ostalih statističkih testova).
Primjer: Provedeno je istraživanje u kojem se želi vidjeti postoji li razlika u vrijednostima dijastoličkog krvnog tlaka između ispitanika koji su primali 1, 2 ili 3 antihipertenziva. U istraživanju je ukupno sudjelovalo 150 ispitanika, gdje je po 50 ispitanika uzimalo kontinuirano 1, 2 ili 3 antihipertenziva. Znači, u ovom se slučaju mijenja situacija u odnosu na t-test, gdje smo imali razliku između dva uzorka ili dva mjerenja. S jedne strane imamo kontinuiranu, metričku varijablu, te s druge strane kvalitativnu, trihotomnu varijablu. Dakle, želimo vidjeti da li između ispitanika/pacijenata koji pripadaju određenoj skupini (1, 2 ili 3 antihipertenziva) postoji razlika u jednoj metričkoj, kontinuiranoj varijabli (dijastolički tlak). Naime, u ovakvim slučajevima ne koristimo t-testove za svaki pojedini par skupina, jer povećavanjem broja t-testova povećavamo vjerojatnost slučajnog pozitivnog nalaza. Tako na primjer, u 20 usporedbi skupina gdje razlike između populacija nema (stvarna razlika jednaka nuli), prosječno će jedno testiranje proglasiti uočene razlike statistički značajnim uz 95% graničnu razinu značajnosti.
Ako izneseno povežemo sa prije iznesenim primjerom koncentracije kolesterola u krvi možemo reći slijedeće: a) ako imamo ispitanika koji ima 35 godina onda njegova koncentracija kolesterola odstupa za neku vrijednost od aritmetičke sredine njegove skupine ispitanika od 30-49 godina b) aritmetička sredina koncentracije kolesterola skupine od 30-49 godina odstupa za neku vrijednost od zajedničke aritmetičke sredine sve četiri skupine ispitanika
6.4.2 Uvjeti za primjenu analize varijance
Neki od uvjeta za primjenu analize varijance su normalitet raspodjele, broj ispitanika po skupinama, metrijske karakteristike varijabli i homogenost varijanci. Ukoliko homogenost varijanci značajno odstupa tada se koristi jedan od testova za provjeru homogenosti varijanci poput Levene test. Ukoliko je malen broj ispitanika po skupinama tada treba napraviti reviziju modela prije primjene analize varijance ili povećati broj ispitanika po pojedinim skupinama. Predmet mjerenja po metrijskim svojstvima je važan kriterij jer ako ne odgovara to je ozbiljno ograničenje za uopće korištenje analize varijance. Predmet mjerenja treba odgovorati intervalnoj ili omjernoj mjernoj ljestvici te također i uvjetima normaliteta raspodjele.
6.4.3 Post hoc testovi
Za primjenu analize varijance i tumačenje značajnosti razlika važno je napomenuti i tzv. post hoc testiranja. Naime, ako dobijemo F-omjer koji je značajan, to znači da se promatrane skupine statistički značajno razlikuju u istraživanoj varijabli. No, još ne možemo tvrditi između kojih parova je razlika značajna! Kako bi provjerili između kojih parova postoji razlika, poželjno je primijeniti jedan od naknadih testova (post hoc) koji slijede nakon analize varijance. U praksi se koriste različiti testovi (Scheffe, Tuckey, Duncan, Newman-Keuls…), a od najčešće korištenih post hoc testova su Scheffeov i HSD Tuckey test. No, potrebno je napomenuti da je Scheffeov post hoc test dosta strog ili ‘konzervativan’ za razliku od HSD Tuckey testa koji je podosta liberalan (izbor ovisi koju statističku pogrešku više želimo izbjeći: tipa 1 ili tipa 2).
Dakle, analiza varijance nije jednostavna metoda i uključuje niz modela: • jednosmjerna (one-way) analiza varijance (ANOVA), s podvrstama za nezavisne i zavisne uzorke (repeated measures ANOVA) • višesmjerna (multi-way) analiza varijance • multifaktorska analiza varijance (MANOVA) • analiza varijance s kontrolom kovarijabli (ANCOVA ili MANCOVA) U gornjim se definicijama smjerovi odnose na nezavisnu varijablu (više smjerova znači više načina kategorizacije), a faktori na zavisnu varijablu (više faktora znači više zavisnih varijabli). Kako smo već definirali, složena analiza varijance uključuje i višesmjernu i multifaktorsku ANOVA-u. Kovarijabla u analizi varijance je metrička varijabla koja može imati utjecaja na rezultata analize jer nije podjednako distribuirana po nezavisnim varijablama. U ANCOVI (MANCOVI) se njen utjecaj matematički odračunava. U višesmjernoj ANOVA-i postoji mogućnost istraživanja međudjelovanja (interakcije) između nezavisnih varijabli, kao u primjeru koji slijedi.
Funkcionalnost R sustava u primjeni različitih modela analize varijance može se vidjeti uporabom dva paketa: car (Fox et al., 2022) i afex (Singmann et al., 2021). Osim navedenih u primjerima će se koristiti još neki paketi koji doprinose olakšavanju primjene i interpretacije analize varijance.
Ulazni model za analizu varijance je ključni dio u razumijevanju konačnog rezultata. Tako, R pomoću funkcije lm ili lmer, omogućava definiranje modela i kontrolu nad procesima obrade rezultata.
If you use R then you probably already know this, but let’s recap anyway. Start with an additive model of Y using the linear model function lm
lm(Y ~ A + B, data=d)
Interactions are expressed succinctly with the asterisk
lm(Y ~ A * B, data=d)
or equivalently but more explicitly by specifying component parts using the colon notation, like
lm(Y ~ A + B + A:B, data=d)
This is useful for more complex interaction structures, e.g.
lm(Y ~ A * B * C, data=d)
which contains all main effects, all two way interactions, and a three way interaction. On the other hand
lm(Y ~ A + B + C + A:B + A:C + B:C, data=d)
is the same except for having no three way interaction.
If you’re feeling fancy you can get the same effect as the model above by raising the variables to a power
lm(Y ~ (A + B + C)**2, data=d) lm(Y ~ (A + B + C)^2, data=d)
which, if you remember your algebra, amounts to the same thing. Frankly I find this a bit too clever, not least because
lm(Y ~ A + B + B**2, data=d)
does not specify a model with a linear effect of A and a quadratic effect of B as every beginning R user and everyone who takes the algebra analogy too seriously feels that it should.
Both of these specifications obey the principle of marginality, which requires, roughly, that all higher order interaction have their lower order siblings in the model unless you have a good reason. (Good reasons are shown below and tend to have to do with nesting). The asterisk and the power notation make sure your models obey this, whereas the colon invites you to forget something.
Squeezing the algebra analogy a bit further, another way to get the all two way interaction model is to make a three way model and then subtract the highest interaction term, like
lm(Y ~ ABC - A:B:C, data=d)
which is cute, but arguably not very useful.
Finally, remember that an intercept is almost always a good idea due to the principle of marginality, so R adds one by default and represents it with a 1. Consequently, these formulae specify the same model
lm(Y ~ A + B, data=d) lm(Y ~ 1 + A + B, data=d)
In the model matrix the intercept really is a column of ones, but R uses it rather more analogically as we will see when specifying mixed models.
In the unlikely event we want to remove the intercept, it can be replaced by a zero, or simply subtracted. Consequently these formulae specify the same, not very sensible, model:
lm(Y ~ 0 + A + B, data=d) lm(Y ~ A + B - 1, data=d) lm(Y ~ -1 + A + B, data=d)
OK, enough warm up. On to the ANOVAs
6.4.4 Nezavisni uzorci
Podaci - Gun, afex example - https://www.psychologie.uni-heidelberg.de/ae/meth/team/mertens/blog/anova_in_r_made_easy.nb.html
library(afex)
data("obk.long")
head(obk.long)## id treatment gender age phase hour value
## 1 1 control M -4.75 pre 1 1
## 2 1 control M -4.75 pre 2 2
## 3 1 control M -4.75 pre 3 4
## 4 1 control M -4.75 pre 4 2
## 5 1 control M -4.75 pre 5 1
## 6 1 control M -4.75 post 1 3Jedan od jako dobrih paketa za primjenu različitih modela analize varijance je lmerTest (Kuznetsova et al., 2020).
lmerTest: Tests in Linear Mixed Effects Models Provides p-values in type I, II or III anova and summary tables for lmer model fits (cf. lme4) via Satterthwaite’s degrees of freedom method. A Kenward-Roger method is also available via the pbkrtest package. Model selection methods include step, drop1 and anova-like tables for random effects (ranova). Methods for Least-Square means (LS-means) and tests of linear contrasts of fixed effects are also available.
Za provedbu post-hoc analize jedan od nezaobilaznih paketa je emmeans (Lenth, 2022)
6.4.7 Izvještaj (output) analize varijance
Jedan od prikladnih načina izvještavanja o rezultatima analize varijance može se dobiti pomoću afex paketa i funkcije nice. Prednost funkcije nice ogleda se u mogućnosti prikaza i dodatnih pokazatelja primjene analize varijance kao što je izračun efekta učinka (Bakeman, 2005; Olejnik & Algina, 2003).
Kod višestrukih usporedbi u modelu analize varijance potrebno je koristiti korigiranu p vrijednost (p-adjusted) te se na taj način izbjegava umnažanje pogreške tipa I (Cramer et al., 2016). U te svrhe koristi se procedura aov (car paket) i anova tablica (anova_table).
6.5 Povezanosti, korelacije
Što je to uopće korelacija? lat. con-sa, relatio-odnos Suodnos ili povezanost dviju varijabli Povezanost pojava može biti: funkcionalna i statistička Iz poznavanja vrijednosti jedne varijable moguće odrediti s određenom vjerojatnošću vrijednost druge varijable Korelacija ukazuje i na DVOSMJERNU povezanost Primjeri: povezanost visine i težine, duljine učenja i ocjene, ocjena i uspješnosti na poslu, količina soli u hrani i kolesterol, visina prihoda i potrošnja… NZV – ZV ali i PREDIKTOR – KRITERIJ Korelacija govori o POVEZANOSTI ali ne i o UZROČNO – POSLJEDIČNOM odnosu
Korelaciju u statistiku među ostalima uvodi Karl Pearson (1857-1936) (Porter, 1988). K. Pearson je bio promotor eugenike, bavio se različitim područjima filozofije i iznimno je utjecao na ogroman značaj kvantitativnih metoda u društvenim znanostima.
Koeficijent korelacije (r) Pokazuje snagu i smjer odnosa između dvije varijable ili događaja ili mjerenja Može poprimiti vrijednost od -1 do +1 a to znači od negativne korelacije do pozitivne korelacije Što je vrijednost korelacije bliže – 1 ili +1 to je snažnija povezanost Vrijednosti koeficijenta korelacija (r) od 0 – 0.25 ili 0 - -0.25 upućuju da nema povezanosti ili je jako slaba, od 0.25 – 0.5 ili -0.25 - -0.5 na slabu ili približno srednju povezanost, od 0.5 – 0.75 ili -0.5 do - -0.75 je umjerena ili dobra povezanost, od 0.75 – 1 ili -0.75 - -1 je izvrsna ili jaka povezanost Uz veličinu koeficijenta korelacija (r), navodi se i značajnost (p) i veličina uzorka (N).
Odnos vrijednosti dviju varijabli mala vrijednost jedne varijable odgovara maloj vrijednosti druge varijable, riječ je o pozitivnoj korelaciji velika vrijednost jedne varijable odgovara velikoj vrijednosti druge varijable, radi se o pozitivnoj korelaciji. mala (niska) vrijednost jedne varijable odgovara velikoj vrijednosti druge varijable i obratno, riječ je o negativnoj korelaciji. Linearan porast jedne varijable odgovara linearno opadanje druge varijable. kada vrijednost jedne varijable u nekim intervalima odgovara maloj vrijednosti druge varijable, a u drugim intervalima velikoj vrijednosti, riječ je o nemonotonoj korelaciji. ukoliko se korelacija više nego jednom mijenja od pozitivne prema negativnoj, takva korelacija naziva se ciklička korelacija kada se na osnovi vrijednosti jedne varijable ne može zaključiti ništa o vrijednosti druge varijable, tada korelacija ne postoji, približno je jednaka nuli.
Vrsta povezanosti i koeficijenti korelacija Linearni odnos između dvije varijable (Pearson koeficijent korelacija, Pearson’s product-moment coefficient) Nelinearni odnos ili varijable koje su na ordinalnoj mjernoj ljestvici (Spearman koeficijent korelacije) Nelinearni odnos ili varijable koje su na nominalnoj i ordinalnoj mjernoj ljestvici (neparametrijski koeficijent korelacije, Kendall tau rang koeficijent korelacije) Nelinearni i zakrivljeni odnosi među varijablama Veći broj varijabli (veći od 2) tada je riječ o jednostavnoj i višestrukoj regresijskoj analizi.
Korelacije u R jeziku je moguće napraviti pomoću jednostavne funkcije cor() a tako i analize kovarijance cov().
6.5.1 Slikovni prikazi
Važnost slikovnog prikaza Slikovno se korelacija prikazuje kao točkasti slikovni prikaz (scatterplot) Točke (pojedinačne vrijednosti) nalaze se oko pravca kojeg nazivamo pravac regresije, regresijski pravac ili linija regresije Što su točke bliže pravcu, veća je korelacija (r) U linearnoj korelaciji, točke se grupiraju oko pravca a kod nelinearne korelacije oko neke druge krivulje Homoscedascitet – jednakost ili jednolikost raspšenosti točaka oko pravca regresije SLIKA VAŽNA – odstupajuće vrijednosti (outliere) značajno mogu promijeniti korelaciju i tumačenje. Iz slikovnog prikaza je vidljivo: a) smjer b) jačina c) oblik d) postojanje outliera…
6.6 Slikovni prikazi za potrebe znanstvenih publikacija
U R jeziku i paketima postoji izvanredan broj mogućnosti vizualizacije analize podataka. Među češće korištenim paketima svakako spadaju funkcije ggplot paketa (Wickham et al., 2022), zatim yarrr (Phillips, 2017) i posebno je za publikacije značajan ggpubr (Kassambara, 2020).
Osim točkastog slikovnog prikaza, korelacije se prikazuju i pomoću korelograma. Korelogram vizualizira matricu koeficijenata korelacija - slikovno.