3.13 Uncertainty and Bias in statistical estimates
Since statistical estimation is a method of inference, we need to weigh external validity evidence the same way we did for hypothesis tests: by considering bias and sampling variability. We can illustrate the difference between bias and sampling variability using the target image below. The center of the target represents the true population parameter. The holes represent statistical estimates. The goal is to get an estimate that “hits” the center of the target:
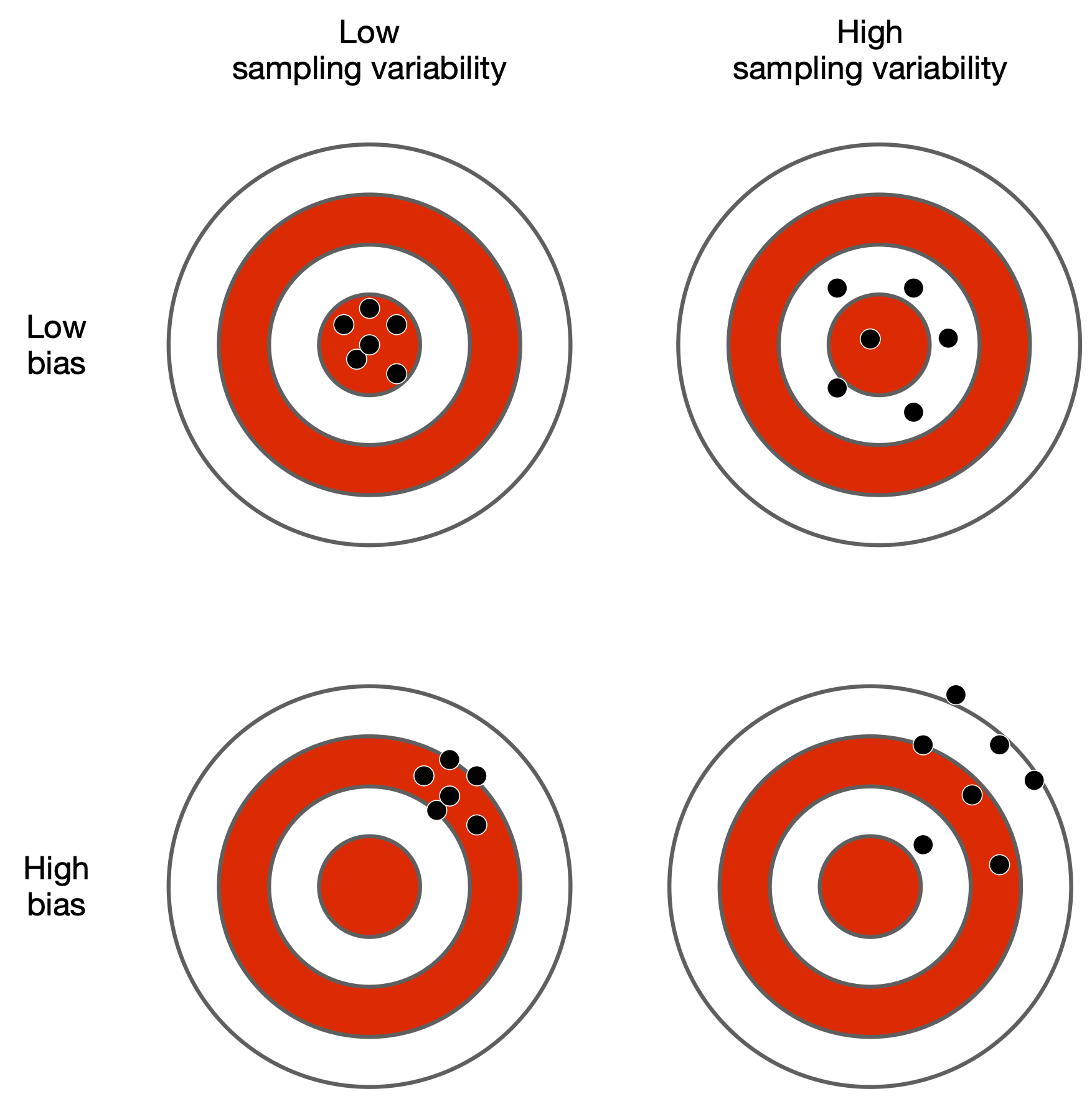
Figure 3.8: Bias and sampling variability
3.13.1 Bias
When the sampling method is unbiased, the estimates will be centered on the true population parameter. This is illustrated with the targets in the top row, where the holes are centered on the bulls eye. On the other hand, when the sampling method is biased, the estimates will be systematically shifted away from the population parameter. This is illustrated with the targets on the bottom row, where the holes are centered away from the bulls eye.
3.13.2 Sampling variabilty
In our target example, the amount sampling variability is shown by how spread out the holes are.
When there is low sampling variability, the statistical estimates from different samples are all fairly close to each other. This is illustrated by the targets in the left column, were the holes are clustered tightly.
When there is high sampling variability, the statistical estimates from different samples are more spread out. This is illustrated by the targets in the right column, were the holes are more spread out.
3.13.3 Back to estimation
Remember the goal of estimation is to estimate a population parameter using a sample. The two reasons that our estimate may not be exactly perfect are sampling variability and bias. In our target example, these are the two reasons why a hole might not exactly hit the center of the target.
We can reduce sampling variability by increasing the sample size. However, we can’t eliminate sampling variability, and therefore there will always be some uncertainty in our estimate due to sampling variability. We can account for the uncertainty due to sampling variation with a compatibility interval. When there is high sampling variability, the compatibility interval will be wider, and when there is low sampling variability, the compatibility interval will be narrower. Either way, we can be fairly confident that the compatibility interval will capture the true population parameter.
However, if a biased sampling method is used the resulting compatibility interval will be biased, and we can’t be confident that the compatibility interval captures the true population parameter. This means that the most important aspect in making a statistical estimate is having an unbiased sampling method. Sample size only matters if the sampling method is unbiased.