4 Análises das matrizes de similaridade
Organização básica
dev.off() #apaga os graficos, se houver algum
rm(list=ls(all=TRUE)) #limpa a memória
cat("\014") #limpa o console 4.1 Importar a base de dados
#dir <- getwd()
#shell.exec(dir) #abre o diretorio de trabalho no Windows Explorer
m_bruta <- read.csv("D:/Elvio/OneDrive/MSS/_Zoo-Rebio/R_ZooRebio.rmd/zoorebio.csv",
sep = ";", dec = ",",
header = T,
row.names = 1,
na.strings = NA)
str(m_bruta)
#View(m_bruta)## 'data.frame': 49 obs. of 85 variables:
## $ Bra.angularis : num 0 0.533 0.533 0 0 ...
## $ Lepadella.sp : num 0 0.178 0.178 0.533 0.178 ...
## $ Lecane.sp : num 0 0 0 0 0 ...
## $ Lec.leontina : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.bulla : num 1.067 0 0.356 0.889 0.178 ...
## $ Lec.cornuta : num 0 0 0 0 0 ...
## $ Lec.curvicornis : num 0 0 0 0 0 ...
## $ Notholca.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.urceolaris : num 0.178 0 0 0 0 ...
## $ Trichocerca.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.quadridentata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.kluchor : num 0.178 0 0 0 0 ...
## $ Lec.lunaris : num 0.356 0.711 1.067 0 0.178 ...
## $ Rotaria.sp : num 0 1.07 0 0 0 ...
## $ Aspelta.sp : num 0.178 0 0 0 0 ...
## $ Lec.furcata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Col.geophila : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.dactyliseta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.calyciflorus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.caudatus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.crepida : num 0 0 0 0 0 ...
## $ Pla.patulus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.ovalis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.elasma : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pla.quadricornis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.aculeata : num 1.6 0.889 0 0.178 0 ...
## $ Ker.tropica : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bdelloidea : num 0 0 0 0 0 ...
## $ Ker.lenzi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Con.unicornis : num 0 0 0 0 0 ...
## $ Alo.dadayi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Macrothrix.sp : num 0.178 0 0 0 0 ...
## $ Alonella.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Nauplii : num 0.711 0.889 0.178 0.889 0.711 ...
## $ Chy.eurynotus : num 0.356 0 0 0 0 ...
## $ Cyclopoida : num 0 0 0 0 0 ...
## $ Mac.collinsi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Copepodite : num 0 0 0 0.178 0 ...
## $ Paracyclops.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Asc.ecaudis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.ovalis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Polyarthra.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.havanaensis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Hexarthra.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.hastata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Tri.tetractis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ker.serrulata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Notodiaptomus.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.falcatus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Fil.longiseta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Myt.crassipes : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.patella : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Euchlanis.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Colurella.sp : num 0 0 0.178 0 0 ...
## $ Mytilina.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.monostyla : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.ligona : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ascomorpha.sp : num 0.178 0 0 0 0 ...
## $ Pom.sulcata : num 0 0 0 0.356 0.356 ...
## $ Harpacticoida : num 0 0 0 0 0 ...
## $ Epi.senta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Rot.neptunia : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dis.aculeata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.luna : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Euc.dilatata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bea.eudactylota : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Chy.sphaericus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.hornemanni : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dia.birgei : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Mac.subquadratus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.quadridentatus: num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pol.vulgaris : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pol.bicerca : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dicranop.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Asc.saltans : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Moi.minuta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Alo.hamulata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Mac.laticornis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Mac.mira : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pro.similis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Alo.pulchella : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dia.spinulosum : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Chydorus.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ily.spinifer : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dun.odontoplax : num 0 0 0 0 0 0 0 0 0 0 ...4.2 Reset point 1
m_trab <- m_brutaAqui substitui-se uma nova matriz de dados, relativizada e/ou transformada, pela matriz bruta.
4.3 Cálculo da matriz de distâncias
Agora vamos calcular a matriz de distâncias (Legendre and Legendre 1998; Borcard, Gillet, and Legendre 2018) entre os pontos de coleta usando a função dist()
4.4 Matriz de distâncias
m_dists <- dist(m_trab, method = "euclidian", diag = TRUE, upper = FALSE)Visualizar a matriz.
#m_dists
str(m_dists)
mode(m_dists)
class(m_dists)
length(as.matrix(m_dists))
as.matrix(m_dists)[1:10, 1:10]## 'dist' num [1:1176] 1.88 2.12 1.71 1.96 2.05 ...
## - attr(*, "Size")= int 49
## - attr(*, "Labels")= chr [1:49] "BB1-P01" "BB1-P02" "BB1-P03" "BB2-P01" ...
## - attr(*, "Diag")= logi TRUE
## - attr(*, "Upper")= logi FALSE
## - attr(*, "method")= chr "euclidean"
## - attr(*, "call")= language dist(x = m_trab, method = "euclidian", diag = TRUE, upper = FALSE)
## [1] "numeric"
## [1] "dist"
## [1] 2401
## BB1-P01 BB1-P02 BB1-P03 BB2-P01 BB2-P02 BB2-P03 BB3-P01 BB3-P02 BB3-P03 BB4-P01
## BB1-P01 0.000000 1.881423 2.118467 1.7144268 1.9555556 2.0502334 1.9636197 1.9716509 1.9716509 4.038335
## BB1-P02 1.881423 0.000000 1.648643 1.8730051 1.6390301 1.6771522 1.9796496 2.4697678 2.3917554 4.214496
## BB1-P03 2.118467 1.648643 0.000000 1.6000000 1.2444444 1.1383332 1.2819738 1.8898037 1.8216801 4.108167
## BB2-P01 1.714427 1.873005 1.600000 0.0000000 0.8709297 1.2057476 1.2187830 1.3063945 1.3063945 3.699316
## BB2-P02 1.955556 1.639030 1.244444 0.8709297 0.0000000 0.5621827 0.9573626 1.6865481 1.5900928 3.866411
## BB2-P03 2.050233 1.677152 1.138333 1.2057476 0.5621827 0.0000000 0.7749154 1.7777778 1.6677034 3.995059
## BB3-P01 1.963620 1.979650 1.281974 1.2187830 0.9573626 0.7749154 0.0000000 1.3184353 1.1657668 3.787960
## BB3-P02 1.971651 2.469768 1.889804 1.3063945 1.6865481 1.7777778 1.3184353 0.0000000 0.5621827 3.433459
## BB3-P03 1.971651 2.391755 1.821680 1.3063945 1.5900928 1.6677034 1.1657668 0.5621827 0.0000000 3.074065
## BB4-P01 4.038335 4.214496 4.108167 3.6993159 3.8664112 3.9950587 3.7879601 3.4334592 3.0740651 0.000000Uma matriz do tipo dist no R é um objeto que armazena as distâncias entre as linhas de uma matriz ou um data frame. Ela é criada pela função dist(), que calcula as distâncias usando diferentes medidas, como “euclidean”, “manhattan”, “canberra”, “binary” ou “minkowski” (Horton and Kleinman 2015).
range(m_trab)
range(m_dists)
min(m_dists)
max(m_dists)
mean(m_dists) #CENTROIDE!! ou Grand mean
sd(m_dists) #standard deviation
centroide <- mean(m_dists)
centroide## [1] 0 72
## [1] 0.3975232 128.2730421
## [1] 0.3975232
## [1] 128.273
## [1] 17.27709
## [1] 27.46556
## [1] 17.27709A função mean() calcula a média de todos os valores da matriz de distâncias, ou seja, a média multivariada, que é o centróide. Nesse caso o centroide assume o valor de 17.3. Usamos agora a fórmula m*(m-1)/2, onde m é o no. de objetos sendo comparados, para calcular quantas distâcias temos na nossa matriz.
length(m_dists)
m <- nrow(as.matrix(m_dists))
m
m*(m-1)/2
summary(m_dists)## [1] 1176
## [1] 49
## [1] 1176
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.3975 2.3366 4.2276 17.2771 12.8234 128.2730Temos então que m é 49 objetos (ou linhas), e portanto, a matriz de distâncias tem 1176 valores. Fazemos agora um breve sumário do que foi calculado até agora com base na matriz de distâncias.
Sumario1 <- cbind(min(m_dists),
max(m_dists),
sd(m_dists),
mean(m_dists),
length(m_dists))
colnames(Sumario1) <- c("Minimo", "Maximo", "Desv.Padr", "Media", "m(m-1)/2")
rownames(Sumario1) <- ("Valores")
Sumario1## Minimo Maximo Desv.Padr Media m(m-1)/2
## Valores 0.3975232 128.273 27.46556 17.27709 11764.5 Calculando a assimetria e a curtose
library(moments)
sk <- skewness(as.matrix(m_dists)) #calcula a assimetria da matriz
ku <- kurtosis(as.matrix(m_dists)) #calcula a curtose da matriz
sku <- cbind(sk,ku) #junta os dois valores em um vetor
colnames(sku) <- c("assimetria", "curtose") #nomeia as colunas do vetor
sku[1:10,] #mostra as primeiras 10 linhas desse vetor
summary(sku) #mostra um resumo estatístico do vetor## assimetria curtose
## BB1-P01 2.979449 10.68082
## BB1-P02 3.000895 10.80319
## BB1-P03 2.965991 10.60747
## BB2-P01 2.970184 10.64078
## BB2-P02 2.966339 10.62497
## BB2-P03 2.961010 10.59150
## BB3-P01 2.953173 10.53677
## BB3-P02 2.964937 10.59193
## BB3-P03 2.964249 10.58770
## BB4-P01 3.020876 10.90521
## assimetria curtose
## Min. :-4.762 Min. :10.54
## 1st Qu.: 2.966 1st Qu.:10.63
## Median : 2.985 Median :10.80
## Mean : 2.507 Mean :12.22
## 3rd Qu.: 3.022 3rd Qu.:11.16
## Max. : 3.312 Max. :34.034.6 Distribuição de frequências da matriz de distâncias
O código abaixo vai plotar um histograma e um boxplot da distribuição de dados armazenada na matriz de distâncias. Também é adicionada uma curva normal teórica ao histograma utilizando a média e o desvio padrão dos dados (Figura 4.1. As funções floor(min(m_dists)) e ceiling(max(m_dists)) definem os limites dos graficos pelo valores mínimo e máximo do objeto.
range(m_dists)## [1] 0.3975232 128.2730421par(mfrow=c(2,1))
hist(m_dists,
breaks = 15, #determina o no. de colunas do histograma
xlim = range(floor(min(m_dists)), ceiling(max(m_dists))),
xlab = "Distr. de Frequências",
freq = FALSE)
curve(dnorm(x, mean=mean(m_dists), sd=sd(m_dists)), add=TRUE)
boxplot.default(m_dists, horizontal = TRUE, frame = FALSE,
xlab="Distr. de Frequências",
ylim=c(floor(min(m_dists)), ceiling(max(m_dists)))) #limites do eixo Y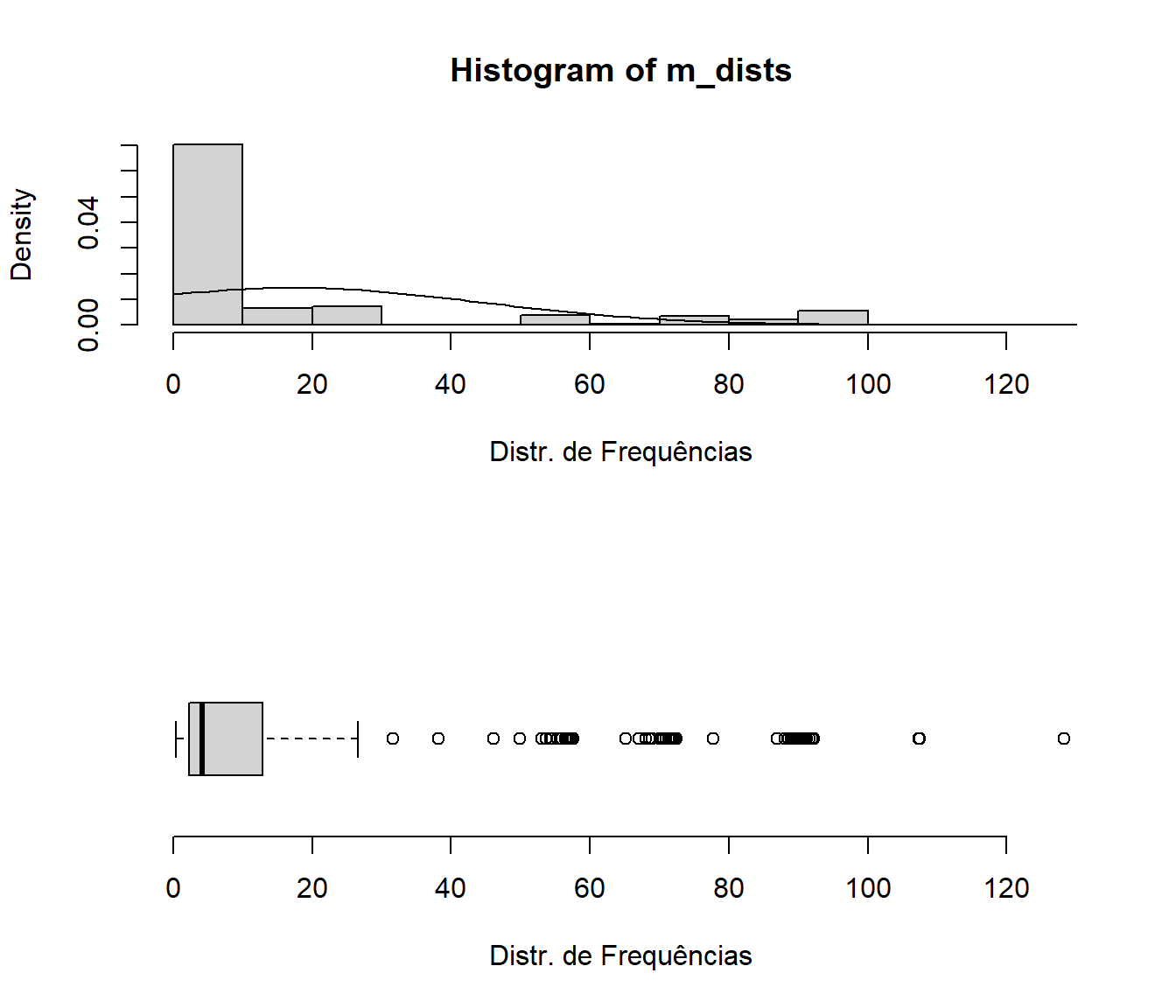
Figure 4.1: Distribuições de frequências da matriz de distâncias
par(mfrow=c(1,1))O comando abaixo apaga os gráficos.
dev.off()4.7 Relativizando e transformando a base de dados
Os códigos para as principais relativizações estão AQUI
library(vegan)
m_relcol <- decostand(m_trab,
method="total",
MARGIN = 2)
#colSums(m_relcol)
#range(m_relcol)
#View(m_relcol)
#m_relcolTransformação pelo arcoseno da raiz quadrada. Os códigos para as principais transformações estão AQUI
m_relcol_asrq <- asin(sqrt(m_relcol))
#View(m_relcol_asrq)
m_relcol_asrqpi <- 2/pi*(asin(sqrt(m_relcol)))
#View(m_relcol_asrqpi)
#rowSums(m_relcol_asrqpi)
#range(m_relcol_asrqpi)4.8 Reset point 2
m_trns <- m_relcol_asrqpi
#m_dists <- dist(m_trns, method = "euclidian", diag = TRUE, upper = FALSE)4.9 Procurando outliers
4.9.1 Listas de distâncias
Lista com as distâncias em desvio padrão entre cada objeto e o centróide, baseado na matriz de distâncias (relativizada/transformada ou bruta, dependendo do arquivo escolhido). As distâncias médias do centróide, expressas em desvios padrão, também podem ser chamadas de z-scores.
library(matrixStats)
m_dists_am <- (as.matrix(m_dists))
centroide_am <- mean(m_dists_am)
av.dist <- (as.matrix(colMeans(m_dists_am, na.rm=T)))
av.desvpad <- (as.matrix(colSds(m_dists_am, na.rm=T)))
dp.centroide_am <- (av.dist-centroide_am)/(colSds(av.dist)) #ou z-scores
list <- as.matrix(cbind(av.dist, av.desvpad, dp.centroide_am))
list## [,1] [,2] [,3]
## BB1-P01 10.366657 21.17447 -0.35004252
## BB1-P02 10.239858 21.22115 -0.35681073
## BB1-P03 10.245557 21.36826 -0.35650657
## BB2-P01 9.910324 21.31641 -0.37440054
## BB2-P02 9.952817 21.39863 -0.37213233
## BB2-P03 10.043020 21.44608 -0.36731750
## BB3-P01 10.012807 21.47299 -0.36893019
## BB3-P02 10.046706 21.29785 -0.36712076
## BB3-P03 9.926650 21.35139 -0.37352908
## BB4-P01 10.737426 20.86363 -0.33025169
## BB4-P02 9.911353 21.45100 -0.37434558
## BB4-P03 9.858023 21.42593 -0.37719222
## BB5-P01 11.826576 20.58031 -0.27211535
## BB5-P02 10.334911 21.10148 -0.35173706
## BB5-P03 9.816750 21.45020 -0.37939529
## BB6-P01 13.306819 20.26184 -0.19310334
## BB6-P02 10.979198 21.00903 -0.31734648
## BB6-P03 11.149078 20.83771 -0.30827865
## CA1-P04 10.092619 21.07106 -0.36467001
## CA1-P05 11.906309 19.88002 -0.26785936
## CA1-P06 10.017961 21.23149 -0.36865508
## CA2-P04 11.267797 20.26701 -0.30194167
## CA2-P05 10.757198 20.55754 -0.32919632
## CA2-P06 10.904969 20.41827 -0.32130862
## CA3-P04 10.113967 21.11491 -0.36353050
## CA3-P05 10.193394 20.90872 -0.35929088
## CA3-P06 9.854828 21.31790 -0.37736278
## CA4-P04 9.825552 21.41124 -0.37892545
## CA4-P05 10.051143 21.38859 -0.36688392
## CA4-P06 10.046077 21.47492 -0.36715433
## CA5-P04 9.768961 21.42554 -0.38194618
## CA5-P05 9.928215 21.37034 -0.37344556
## CA5-P06 10.001365 21.38745 -0.36954098
## CA6-P04 28.450374 14.20741 0.61522527
## CA6-P05 13.908976 19.89047 -0.16096155
## CA6-P06 9.994444 21.48038 -0.36991039
## EN08 10.525473 21.27891 -0.34156528
## EN09 10.620472 20.99889 -0.33649445
## EN10 11.545458 20.85078 -0.28712079
## EN11 89.716061 14.56606 3.88544876
## EN12 89.292543 14.24555 3.86284232
## EN13 10.602997 21.05735 -0.33742723
## EN15 69.913680 12.92970 2.82844252
## EN16 56.153862 11.86904 2.09397467
## EN14 17.545242 17.84089 0.03313406
## EN17 16.166545 18.98282 -0.04045763
## RE19 10.853765 20.86100 -0.32404176
## RE18 11.852152 20.45576 -0.27075014
## RE07 28.763310 15.83638 0.63192914Ordenamos as distâncias da maior para a menor
colnames(list, do.NULL = FALSE)
colnames(list) <- c("Av.Dist", "Av.StDev", "DP.Centroide")
list2 <- list[order(list[,1], decreasing = TRUE),] #[,1] ou o nome da coluna
list2## [1] "col1" "col2" "col3"
## Av.Dist Av.StDev DP.Centroide
## EN11 89.716061 14.56606 3.88544876
## EN12 89.292543 14.24555 3.86284232
## EN15 69.913680 12.92970 2.82844252
## EN16 56.153862 11.86904 2.09397467
## RE07 28.763310 15.83638 0.63192914
## CA6-P04 28.450374 14.20741 0.61522527
## EN14 17.545242 17.84089 0.03313406
## EN17 16.166545 18.98282 -0.04045763
## CA6-P05 13.908976 19.89047 -0.16096155
## BB6-P01 13.306819 20.26184 -0.19310334
## CA1-P05 11.906309 19.88002 -0.26785936
## RE18 11.852152 20.45576 -0.27075014
## BB5-P01 11.826576 20.58031 -0.27211535
## EN10 11.545458 20.85078 -0.28712079
## CA2-P04 11.267797 20.26701 -0.30194167
## BB6-P03 11.149078 20.83771 -0.30827865
## BB6-P02 10.979198 21.00903 -0.31734648
## CA2-P06 10.904969 20.41827 -0.32130862
## RE19 10.853765 20.86100 -0.32404176
## CA2-P05 10.757198 20.55754 -0.32919632
## BB4-P01 10.737426 20.86363 -0.33025169
## EN09 10.620472 20.99889 -0.33649445
## EN13 10.602997 21.05735 -0.33742723
## EN08 10.525473 21.27891 -0.34156528
## BB1-P01 10.366657 21.17447 -0.35004252
## BB5-P02 10.334911 21.10148 -0.35173706
## BB1-P03 10.245557 21.36826 -0.35650657
## BB1-P02 10.239858 21.22115 -0.35681073
## CA3-P05 10.193394 20.90872 -0.35929088
## CA3-P04 10.113967 21.11491 -0.36353050
## CA1-P04 10.092619 21.07106 -0.36467001
## CA4-P05 10.051143 21.38859 -0.36688392
## BB3-P02 10.046706 21.29785 -0.36712076
## CA4-P06 10.046077 21.47492 -0.36715433
## BB2-P03 10.043020 21.44608 -0.36731750
## CA1-P06 10.017961 21.23149 -0.36865508
## BB3-P01 10.012807 21.47299 -0.36893019
## CA5-P06 10.001365 21.38745 -0.36954098
## CA6-P06 9.994444 21.48038 -0.36991039
## BB2-P02 9.952817 21.39863 -0.37213233
## CA5-P05 9.928215 21.37034 -0.37344556
## BB3-P03 9.926650 21.35139 -0.37352908
## BB4-P02 9.911353 21.45100 -0.37434558
## BB2-P01 9.910324 21.31641 -0.37440054
## BB4-P03 9.858023 21.42593 -0.37719222
## CA3-P06 9.854828 21.31790 -0.37736278
## CA4-P04 9.825552 21.41124 -0.37892545
## BB5-P03 9.816750 21.45020 -0.37939529
## CA5-P04 9.768961 21.42554 -0.381946184.9.2 Distribuição de frequências das distâncias médias para o centróide Av.Dist
Observe o valor máximo e mínimo gerados pela função range() e substitua nas linhas de código assinaladas com #. Aqui o menor valor foi 9.7689607 e o maior valor foi 89.7160615. Use valores maiores para facilitar a visualização no gráfico (Figura 4.2).
range(av.dist)## [1] 9.768961 89.716061par(mfrow=c(3,1))
hist(list2[, "Av.Dist"],
breaks = 15, #determina o no. de colunas do histograma
xlab = "Distr. de Frequências das Distâncias (em dp) para o centroide",
main = "Distribuição de Frequência da distância média para o centroide",
xlim = range(floor(min(av.dist)), ceiling(max(av.dist))), #substitua aqui o menor e maior valor do `range()`
freq = T)
hist(list2[, "Av.Dist"],
breaks = 15, #determina o no. de colunas do histograma
xlab = "Distr. de Frequências das Distâncias (em dp) para o centroide",
main = "Curva de normalidade ajustada para a Distribuição de Frequência",
xlim = range(floor(min(av.dist)), ceiling(max(av.dist))), #substitua aqui o menor e maior valor do `range()`
freq = F)
curve(dnorm(x, mean=mean(list2[, "Av.Dist"]), sd=sd(list2[, "Av.Dist"])), add=TRUE)
boxplot.default(list2[, "Av.Dist"], horizontal = TRUE, frame = FALSE,
xlab="Distr. de Frequências",
ylim=c(floor(min(av.dist)), ceiling(max(av.dist)))) #substitua aqui o menor e maior valor do `range()`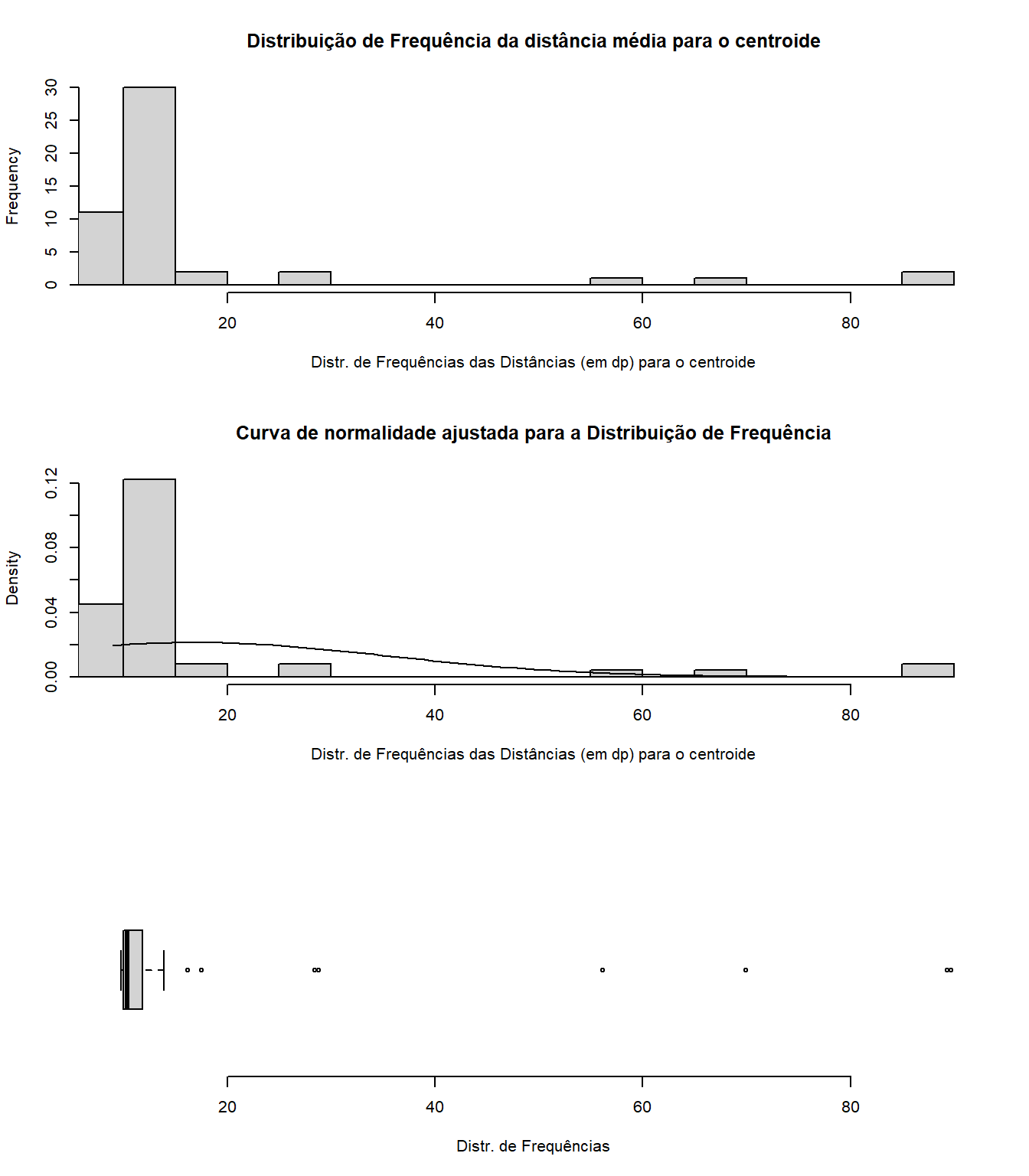
Figure 4.2: Distribuição de frequências das distâncias médias para o centroide.
par(mfrow=c(1,1))4.9.2.1 Distribuição de frequências dos desvios padões das distâncias médias para o centróide DP.Centroide
Observe o valor máximo e mínimo gerados pela função range() e substitua nas linhas de código assinaladas com #. Aqui o menor valor foi -0.3819462 e o maior valor foi 3.8854488. Use valores maiores para facilitar a visualização no gráfico (Figura 4.3).
range(dp.centroide_am)## [1] -0.3819462 3.8854488par(mfrow=c(3,1))
hist(list2[, "DP.Centroide"],
breaks = 15, #determina o no. de colunas do histograma
xlab = "Distr. de Frequências das Distâncias dos desvios padões para o centroide",
main = "Distribuição de Frequência dos desvio padões das distâncias médias para o centroide",
xlim = range(floor(min(dp.centroide_am)), ceiling(max(dp.centroide_am))), #substitua aqui o menor e maior valor do `range()`
freq = T)
hist(list2[, "DP.Centroide"],
breaks = 15, #determina o no. de colunas do histograma
xlab = "Distr. de Frequências das Distâncias dos desvios padrões das distâncias médias para o centroide",
main = "Curva de normalidade ajustada para a Distribuição de Frequência",
xlim = range(floor(min(dp.centroide_am)), ceiling(max(dp.centroide_am))), #substitua aqui o menor e maior valor do `range()`
freq = F)
curve(dnorm(x, mean=mean(list2[, "DP.Centroide"]), sd=sd(list2[, "DP.Centroide"])), add=TRUE)
boxplot.default(list2[, "DP.Centroide"], horizontal = TRUE, frame = FALSE,
xlab="Distr. de Frequências",
ylim=c(floor(min(dp.centroide_am)), ceiling(max(dp.centroide_am)))) #substitua aqui o menor e maior valor do `range()`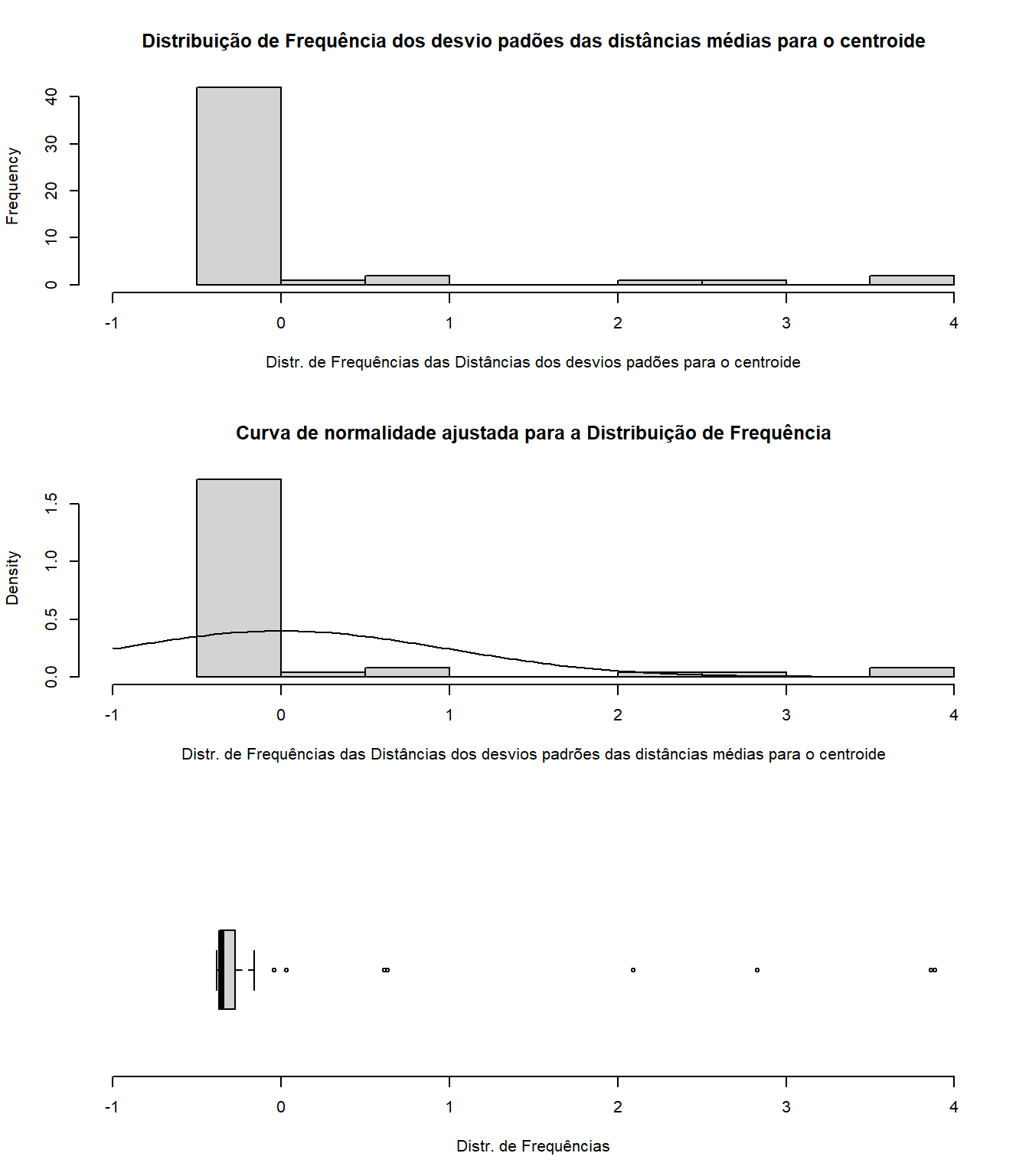
Figure 4.3: Distribuição de frequências dos desvios padões das distâncias médias para o centroide.
par(mfrow=c(1,1))Se necessário apague os gráficos
dev.off()4.10 Lista final de outliers
Agora fazemos a lista final de distâncias com os outliers baseados em um ‘cutoff’.
cutoff <- 2.0Note que o ‘cutoff’ foi estabelecido no código acima no vetor ‘cutoff <-’. Ou seja, o ‘cutoff’ definindo quem serão considerados outliers, foi estabelecido como sendo valores de +2.0 e -2.0 desvios padrões da média multivariada ou centroide. Valores acima ou abaixo do ‘cutoff’ definido recebem o nome “OUTLIER”, na coluna “Outliers”. Criada com o código abaixo.
library(gt)
format(cutoff, nsmall = 1)
listf <- as.data.frame(list2)
listf$Outliers <- ifelse(listf$DP.Centroide>-cutoff & listf$DP.Centroide<cutoff, "", "OUTLIER")
listf
gt(cbind(Sítios=rownames(listf),listf))## [1] "2.0"
## Av.Dist Av.StDev DP.Centroide Outliers
## EN11 89.716061 14.56606 3.88544876 OUTLIER
## EN12 89.292543 14.24555 3.86284232 OUTLIER
## EN15 69.913680 12.92970 2.82844252 OUTLIER
## EN16 56.153862 11.86904 2.09397467 OUTLIER
## RE07 28.763310 15.83638 0.63192914
## CA6-P04 28.450374 14.20741 0.61522527
## EN14 17.545242 17.84089 0.03313406
## EN17 16.166545 18.98282 -0.04045763
## CA6-P05 13.908976 19.89047 -0.16096155
## BB6-P01 13.306819 20.26184 -0.19310334
## CA1-P05 11.906309 19.88002 -0.26785936
## RE18 11.852152 20.45576 -0.27075014
## BB5-P01 11.826576 20.58031 -0.27211535
## EN10 11.545458 20.85078 -0.28712079
## CA2-P04 11.267797 20.26701 -0.30194167
## BB6-P03 11.149078 20.83771 -0.30827865
## BB6-P02 10.979198 21.00903 -0.31734648
## CA2-P06 10.904969 20.41827 -0.32130862
## RE19 10.853765 20.86100 -0.32404176
## CA2-P05 10.757198 20.55754 -0.32919632
## BB4-P01 10.737426 20.86363 -0.33025169
## EN09 10.620472 20.99889 -0.33649445
## EN13 10.602997 21.05735 -0.33742723
## EN08 10.525473 21.27891 -0.34156528
## BB1-P01 10.366657 21.17447 -0.35004252
## BB5-P02 10.334911 21.10148 -0.35173706
## BB1-P03 10.245557 21.36826 -0.35650657
## BB1-P02 10.239858 21.22115 -0.35681073
## CA3-P05 10.193394 20.90872 -0.35929088
## CA3-P04 10.113967 21.11491 -0.36353050
## CA1-P04 10.092619 21.07106 -0.36467001
## CA4-P05 10.051143 21.38859 -0.36688392
## BB3-P02 10.046706 21.29785 -0.36712076
## CA4-P06 10.046077 21.47492 -0.36715433
## BB2-P03 10.043020 21.44608 -0.36731750
## CA1-P06 10.017961 21.23149 -0.36865508
## BB3-P01 10.012807 21.47299 -0.36893019
## CA5-P06 10.001365 21.38745 -0.36954098
## CA6-P06 9.994444 21.48038 -0.36991039
## BB2-P02 9.952817 21.39863 -0.37213233
## CA5-P05 9.928215 21.37034 -0.37344556
## BB3-P03 9.926650 21.35139 -0.37352908
## BB4-P02 9.911353 21.45100 -0.37434558
## BB2-P01 9.910324 21.31641 -0.37440054
## BB4-P03 9.858023 21.42593 -0.37719222
## CA3-P06 9.854828 21.31790 -0.37736278
## CA4-P04 9.825552 21.41124 -0.37892545
## BB5-P03 9.816750 21.45020 -0.37939529
## CA5-P04 9.768961 21.42554 -0.38194618| Sítios | Av.Dist | Av.StDev | DP.Centroide | Outliers |
|---|---|---|---|---|
| EN11 | 89.716061 | 14.56606 | 3.88544876 | OUTLIER |
| EN12 | 89.292543 | 14.24555 | 3.86284232 | OUTLIER |
| EN15 | 69.913680 | 12.92970 | 2.82844252 | OUTLIER |
| EN16 | 56.153862 | 11.86904 | 2.09397467 | OUTLIER |
| RE07 | 28.763310 | 15.83638 | 0.63192914 | |
| CA6-P04 | 28.450374 | 14.20741 | 0.61522527 | |
| EN14 | 17.545242 | 17.84089 | 0.03313406 | |
| EN17 | 16.166545 | 18.98282 | -0.04045763 | |
| CA6-P05 | 13.908976 | 19.89047 | -0.16096155 | |
| BB6-P01 | 13.306819 | 20.26184 | -0.19310334 | |
| CA1-P05 | 11.906309 | 19.88002 | -0.26785936 | |
| RE18 | 11.852152 | 20.45576 | -0.27075014 | |
| BB5-P01 | 11.826576 | 20.58031 | -0.27211535 | |
| EN10 | 11.545458 | 20.85078 | -0.28712079 | |
| CA2-P04 | 11.267797 | 20.26701 | -0.30194167 | |
| BB6-P03 | 11.149078 | 20.83771 | -0.30827865 | |
| BB6-P02 | 10.979198 | 21.00903 | -0.31734648 | |
| CA2-P06 | 10.904969 | 20.41827 | -0.32130862 | |
| RE19 | 10.853765 | 20.86100 | -0.32404176 | |
| CA2-P05 | 10.757198 | 20.55754 | -0.32919632 | |
| BB4-P01 | 10.737426 | 20.86363 | -0.33025169 | |
| EN09 | 10.620472 | 20.99889 | -0.33649445 | |
| EN13 | 10.602997 | 21.05735 | -0.33742723 | |
| EN08 | 10.525473 | 21.27891 | -0.34156528 | |
| BB1-P01 | 10.366657 | 21.17447 | -0.35004252 | |
| BB5-P02 | 10.334911 | 21.10148 | -0.35173706 | |
| BB1-P03 | 10.245557 | 21.36826 | -0.35650657 | |
| BB1-P02 | 10.239858 | 21.22115 | -0.35681073 | |
| CA3-P05 | 10.193394 | 20.90872 | -0.35929088 | |
| CA3-P04 | 10.113967 | 21.11491 | -0.36353050 | |
| CA1-P04 | 10.092619 | 21.07106 | -0.36467001 | |
| CA4-P05 | 10.051143 | 21.38859 | -0.36688392 | |
| BB3-P02 | 10.046706 | 21.29785 | -0.36712076 | |
| CA4-P06 | 10.046077 | 21.47492 | -0.36715433 | |
| BB2-P03 | 10.043020 | 21.44608 | -0.36731750 | |
| CA1-P06 | 10.017961 | 21.23149 | -0.36865508 | |
| BB3-P01 | 10.012807 | 21.47299 | -0.36893019 | |
| CA5-P06 | 10.001365 | 21.38745 | -0.36954098 | |
| CA6-P06 | 9.994444 | 21.48038 | -0.36991039 | |
| BB2-P02 | 9.952817 | 21.39863 | -0.37213233 | |
| CA5-P05 | 9.928215 | 21.37034 | -0.37344556 | |
| BB3-P03 | 9.926650 | 21.35139 | -0.37352908 | |
| BB4-P02 | 9.911353 | 21.45100 | -0.37434558 | |
| BB2-P01 | 9.910324 | 21.31641 | -0.37440054 | |
| BB4-P03 | 9.858023 | 21.42593 | -0.37719222 | |
| CA3-P06 | 9.854828 | 21.31790 | -0.37736278 | |
| CA4-P04 | 9.825552 | 21.41124 | -0.37892545 | |
| BB5-P03 | 9.816750 | 21.45020 | -0.37939529 | |
| CA5-P04 | 9.768961 | 21.42554 | -0.38194618 |
4.11 Particionando a matriz
Talvez seja necessário particionar a matriz atua de trabalho para remover os outliers. Isso pode ser feito com os códigos abaixo que definem os outliers no vetor outlier_sites. Ele define quais objetos ou UA’s serão particionados.
outlier_sites <- rownames(listf)[listf$Outliers == "OUTLIER"]
outlier_sites
m_part_out <- m_trns[!(row.names(m_trns) %in% c(outlier_sites)),]
m_part_out
str(m_part_out)## [1] "EN11" "EN12" "EN15" "EN16"
## Bra.angularis Lepadella.sp Lecane.sp Lec.leontina Lec.bulla Lec.cornuta Lec.curvicornis Notholca.sp
## BB1-P01 0.0000000 0.00000000 0.0000000 0 0.05893968 0.0000000 0.0000000 0
## BB1-P02 0.3690101 0.07856172 0.0000000 0 0.00000000 0.0000000 0.0000000 0
## BB1-P03 0.3690101 0.07856172 0.0000000 0 0.03399641 0.0000000 0.0000000 0
## BB2-P01 0.0000000 0.13677765 0.0000000 0 0.05379148 0.0000000 0.0000000 0
## BB2-P02 0.0000000 0.07856172 0.0000000 0 0.02403337 0.0000000 0.0000000 0
## BB2-P03 0.0000000 0.07856172 0.0000000 0 0.00000000 0.0000000 0.0000000 0
## BB3-P01 0.0000000 0.00000000 0.3333333 0 0.04164684 0.1131341 0.0000000 0
## BB3-P02 0.0000000 0.00000000 0.0000000 0 0.07223791 0.0000000 0.0000000 0
## BB3-P03 0.0000000 0.00000000 0.0000000 0 0.06809025 0.1131341 0.0000000 0
## BB4-P01 0.0000000 0.00000000 0.0000000 0 0.06809025 0.0000000 0.1473631 0
## BB4-P02 0.0000000 0.00000000 0.0000000 0 0.03399641 0.0000000 0.0000000 1
## Bra.urceolaris Trichocerca.sp Lec.quadridentata Lec.kluchor Lec.lunaris Rotaria.sp Aspelta.sp Lec.furcata
## BB1-P01 0.3918266 0 0 0.2467517 0.11788372 0.00000000 0.1949822 0
## BB1-P02 0.0000000 0 0 0.0000000 0.16769424 0.07645609 0.0000000 0
## BB1-P03 0.0000000 0 0 0.0000000 0.20662441 0.00000000 0.0000000 0
## BB2-P01 0.0000000 0 0 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB2-P02 0.0000000 0 0 0.0000000 0.08311677 0.00000000 0.0000000 0
## BB2-P03 0.0000000 0 0 0.0000000 0.08311677 0.00000000 0.0000000 0
## BB3-P01 0.0000000 0 0 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB3-P02 0.0000000 0 0 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB3-P03 0.0000000 0 0 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB4-P01 0.0000000 0 0 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB4-P02 0.0000000 0 0 0.0000000 0.00000000 0.04407110 0.0000000 0
## Col.geophila Lep.dactyliseta Bra.calyciflorus Bra.caudatus Lec.crepida Pla.patulus Lec.ovalis Lec.elasma
## BB1-P01 0 0 0 0 0.0000000 0 0 0
## BB1-P02 0 0 0 0 0.0000000 0 0 0
## BB1-P03 0 0 0 0 0.0000000 0 0 0
## BB2-P01 0 0 0 0 0.0000000 0 0 0
## BB2-P02 0 0 0 0 0.0000000 0 0 0
## BB2-P03 0 0 0 0 0.2163469 0 0 0
## BB3-P01 0 0 0 0 0.0000000 0 0 0
## BB3-P02 0 0 0 0 0.0000000 0 0 0
## BB3-P03 0 0 0 0 0.0000000 0 0 0
## BB4-P01 0 0 0 0 0.0000000 0 0 0
## BB4-P02 0 0 0 0 0.0000000 0 0 0
## Pla.quadricornis Lec.aculeata Ker.tropica Bdelloidea Ker.lenzi Con.unicornis Alo.dadayi Macrothrix.sp
## BB1-P01 0 0.4418018 0 0.00000000 0 0.0000000 0 0.1949822
## BB1-P02 0 0.3163570 0 0.00000000 0 0.0000000 0 0.0000000
## BB1-P03 0 0.0000000 0 0.00000000 0 0.0000000 0 0.0000000
## BB2-P01 0 0.1367777 0 0.00000000 0 0.0000000 0 0.0000000
## BB2-P02 0 0.0000000 0 0.00000000 0 0.0000000 0 0.0000000
## BB2-P03 0 0.0000000 0 0.00000000 0 0.0000000 0 0.0000000
## BB3-P01 0 0.0000000 0 0.03451711 0 0.0000000 0 0.0000000
## BB3-P02 0 0.0000000 0 0.04883854 0 0.5000000 0 0.0000000
## BB3-P03 0 0.0000000 0 0.06913621 0 0.3918266 0 0.0000000
## BB4-P01 0 0.0000000 0 0.15584137 0 0.0000000 0 0.0000000
## BB4-P02 0 0.0000000 0 0.09159462 0 0.0000000 0 0.0000000
## Alonella.sp Nauplii Chy.eurynotus Cyclopoida Mac.collinsi Copepodite Paracyclops.sp Asc.ecaudis Lep.ovalis
## BB1-P01 0 0.03510911 0.3333333 0.00000000 0 0.00000000 0 0 0
## BB1-P02 0 0.03925816 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB1-P03 0 0.01754788 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB2-P01 0 0.03925816 0.0000000 0.00000000 0 0.05569274 0 0 0
## BB2-P02 0 0.03510911 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB2-P03 0 0.02481960 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB3-P01 0 0.00000000 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB3-P02 0 0.02481960 0.0000000 0.09862661 0 0.05569274 0 0 0
## BB3-P03 0 0.02481960 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB4-P01 0 0.04967702 0.0000000 0.00000000 0 0.05569274 0 0 0
## BB4-P02 0 0.01754788 0.0000000 0.00000000 0 0.00000000 0 0 0
## Polyarthra.sp Bra.havanaensis Hexarthra.sp Lec.hastata Tri.tetractis Ker.serrulata Notodiaptomus.sp Bra.falcatus
## BB1-P01 0 0 0 0 0 0 0 0
## BB1-P02 0 0 0 0 0 0 0 0
## BB1-P03 0 0 0 0 0 0 0 0
## BB2-P01 0 0 0 0 0 0 0 0
## BB2-P02 0 0 0 0 0 0 0 0
## BB2-P03 0 0 0 0 0 0 0 0
## BB3-P01 0 0 0 0 0 0 0 0
## BB3-P02 0 0 0 0 0 0 0 0
## BB3-P03 0 0 0 0 0 0 0 0
## BB4-P01 0 0 0 0 0 0 0 0
## BB4-P02 0 0 0 0 0 0 0 0
## Fil.longiseta Myt.crassipes Lep.patella Euchlanis.sp Colurella.sp Mytilina.sp Lec.monostyla Lec.ligona
## BB1-P01 0 0 0 0 0.00000000 0 0 0
## BB1-P02 0 0 0 0 0.00000000 0 0 0
## BB1-P03 0 0 0 0 0.09634135 0 0 0
## BB2-P01 0 0 0 0 0.00000000 0 0 0
## BB2-P02 0 0 0 0 0.00000000 0 0 0
## BB2-P03 0 0 0 0 0.00000000 0 0 0
## BB3-P01 0 0 0 0 0.00000000 0 0 0
## BB3-P02 0 0 0 0 0.00000000 0 0 0
## BB3-P03 0 0 0 0 0.00000000 0 0 0
## BB4-P01 0 0 0 0 0.00000000 0 0 0
## BB4-P02 0 0 0 0 0.00000000 0 0 0
## Ascomorpha.sp Pom.sulcata Harpacticoida Epi.senta Rot.neptunia Dis.aculeata Lec.luna Euc.dilatata
## BB1-P01 1 0.0 0 0 0 0 0 0
## BB1-P02 0 0.0 0 0 0 0 0 0
## BB1-P03 0 0.0 0 0 0 0 0 0
## BB2-P01 0 0.5 0 0 0 0 0 0
## BB2-P02 0 0.5 0 0 0 0 0 0
## BB2-P03 0 0.0 0 0 0 0 0 0
## BB3-P01 0 0.0 0 0 0 0 0 0
## BB3-P02 0 0.0 1 0 0 0 0 0
## BB3-P03 0 0.0 0 0 0 0 0 0
## BB4-P01 0 0.0 0 0 0 0 0 0
## BB4-P02 0 0.0 0 1 0 0 0 0
## Bea.eudactylota Chy.sphaericus Lec.hornemanni Dia.birgei Mac.subquadratus Bra.quadridentatus Pol.vulgaris
## BB1-P01 0 0 0 0 0 0 0
## BB1-P02 0 0 0 0 0 0 0
## BB1-P03 0 0 0 0 0 0 0
## BB2-P01 0 0 0 0 0 0 0
## BB2-P02 0 0 0 0 0 0 0
## BB2-P03 0 0 0 0 0 0 0
## BB3-P01 0 0 0 0 0 0 0
## BB3-P02 0 0 0 0 0 0 0
## BB3-P03 0 0 0 0 0 0 0
## BB4-P01 0 0 0 0 0 0 0
## BB4-P02 0 0 0 0 0 0 0
## Pol.bicerca Dicranop.sp Asc.saltans Moi.minuta Alo.hamulata Mac.laticornis Mac.mira Pro.similis Alo.pulchella
## BB1-P01 0 0 0 0 0 0 0 0 0
## BB1-P02 0 0 0 0 0 0 0 0 0
## BB1-P03 0 0 0 0 0 0 0 0 0
## BB2-P01 0 0 0 0 0 0 0 0 0
## BB2-P02 0 0 0 0 0 0 0 0 0
## BB2-P03 0 0 0 0 0 0 0 0 0
## BB3-P01 0 0 0 0 0 0 0 0 0
## BB3-P02 0 0 0 0 0 0 0 0 0
## BB3-P03 0 0 0 0 0 0 0 0 0
## BB4-P01 0 0 0 0 0 0 0 0 0
## BB4-P02 0 0 0 0 0 0 0 0 0
## Dia.spinulosum Chydorus.sp Ily.spinifer Dun.odontoplax
## BB1-P01 0 0 0 0
## BB1-P02 0 0 0 0
## BB1-P03 0 0 0 0
## BB2-P01 0 0 0 0
## BB2-P02 0 0 0 0
## BB2-P03 0 0 0 0
## BB3-P01 0 0 0 0
## BB3-P02 0 0 0 0
## BB3-P03 0 0 0 0
## BB4-P01 0 0 0 0
## BB4-P02 0 0 0 0
## [ reached 'max' / getOption("max.print") -- omitted 34 rows ]
## 'data.frame': 45 obs. of 85 variables:
## $ Bra.angularis : num 0 0.369 0.369 0 0 ...
## $ Lepadella.sp : num 0 0.0786 0.0786 0.1368 0.0786 ...
## $ Lecane.sp : num 0 0 0 0 0 ...
## $ Lec.leontina : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.bulla : num 0.0589 0 0.034 0.0538 0.024 ...
## $ Lec.cornuta : num 0 0 0 0 0 ...
## $ Lec.curvicornis : num 0 0 0 0 0 ...
## $ Notholca.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.urceolaris : num 0.392 0 0 0 0 ...
## $ Trichocerca.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.quadridentata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.kluchor : num 0.247 0 0 0 0 ...
## $ Lec.lunaris : num 0.1179 0.1677 0.2066 0 0.0831 ...
## $ Rotaria.sp : num 0 0.0765 0 0 0 ...
## $ Aspelta.sp : num 0.195 0 0 0 0 ...
## $ Lec.furcata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Col.geophila : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.dactyliseta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.calyciflorus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.caudatus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.crepida : num 0 0 0 0 0 ...
## $ Pla.patulus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.ovalis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.elasma : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pla.quadricornis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.aculeata : num 0.442 0.316 0 0.137 0 ...
## $ Ker.tropica : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bdelloidea : num 0 0 0 0 0 ...
## $ Ker.lenzi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Con.unicornis : num 0 0 0 0 0 ...
## $ Alo.dadayi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Macrothrix.sp : num 0.195 0 0 0 0 ...
## $ Alonella.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Nauplii : num 0.0351 0.0393 0.0175 0.0393 0.0351 ...
## $ Chy.eurynotus : num 0.333 0 0 0 0 ...
## $ Cyclopoida : num 0 0 0 0 0 ...
## $ Mac.collinsi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Copepodite : num 0 0 0 0.0557 0 ...
## $ Paracyclops.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Asc.ecaudis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.ovalis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Polyarthra.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.havanaensis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Hexarthra.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.hastata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Tri.tetractis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ker.serrulata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Notodiaptomus.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.falcatus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Fil.longiseta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Myt.crassipes : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.patella : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Euchlanis.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Colurella.sp : num 0 0 0.0963 0 0 ...
## $ Mytilina.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.monostyla : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.ligona : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ascomorpha.sp : num 1 0 0 0 0 0 0 0 0 0 ...
## $ Pom.sulcata : num 0 0 0 0.5 0.5 0 0 0 0 0 ...
## $ Harpacticoida : num 0 0 0 0 0 0 0 1 0 0 ...
## $ Epi.senta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Rot.neptunia : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dis.aculeata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.luna : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Euc.dilatata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bea.eudactylota : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Chy.sphaericus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.hornemanni : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dia.birgei : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Mac.subquadratus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.quadridentatus: num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pol.vulgaris : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pol.bicerca : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dicranop.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Asc.saltans : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Moi.minuta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Alo.hamulata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Mac.laticornis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Mac.mira : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pro.similis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Alo.pulchella : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dia.spinulosum : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Chydorus.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ily.spinifer : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dun.odontoplax : num 0 0 0 0 0 0 0 0 0 0 ...Criamos uma nova matriz particionada m_part_out sem os EN11, EN12, EN15, EN16, que apresentavam valores além do cutoff previamente definido para outliers.
sum_part <- colSums(m_part_out)
sum_part
m_part <- m_part_out[(colSums(m_part_out) != 0)] #em != a exclamação inverte o sentido
zero_sum_cols <- names(which(colSums(m_part_out) == 0))
zero_sum_cols #nomes das espécies zeradas
str(m_part)
sum_m_part <- colSums(m_part)
sum_m_part
m_part
length(as.matrix(m_part))## Bra.angularis Lepadella.sp Lecane.sp Lec.leontina Lec.bulla Lec.cornuta
## 1.3118631 2.2390217 1.0000000 1.0715261 2.0514645 1.1031787
## Lec.curvicornis Notholca.sp Bra.urceolaris Trichocerca.sp Lec.quadridentata Lec.kluchor
## 0.6306022 1.0000000 1.1754797 1.3906576 1.4326938 1.3068915
## Lec.lunaris Rotaria.sp Aspelta.sp Lec.furcata Col.geophila Lep.dactyliseta
## 2.1090000 2.1050221 1.4090954 0.3743807 1.0000000 1.0825147
## Bra.calyciflorus Bra.caudatus Lec.crepida Pla.patulus Lec.ovalis Lec.elasma
## 1.0000000 1.0000000 1.3125056 0.3698601 1.1754797 1.0000000
## Pla.quadricornis Lec.aculeata Ker.tropica Bdelloidea Ker.lenzi Con.unicornis
## 1.0000000 1.5132892 1.0000000 2.6638819 1.1666667 1.1595470
## Alo.dadayi Macrothrix.sp Alonella.sp Nauplii Chy.eurynotus Cyclopoida
## 1.4261054 0.3899645 1.2767999 1.9045455 1.5868805 1.4321709
## Mac.collinsi Copepodite Paracyclops.sp Asc.ecaudis Lep.ovalis Polyarthra.sp
## 1.0000000 1.9923047 1.0000000 1.0000000 1.5714360 1.0000000
## Bra.havanaensis Hexarthra.sp Lec.hastata Tri.tetractis Ker.serrulata Notodiaptomus.sp
## 1.0000000 1.0000000 0.2048328 0.4979181 1.0000000 1.0000000
## Bra.falcatus Fil.longiseta Myt.crassipes Lep.patella Euchlanis.sp Colurella.sp
## 0.2132229 1.0000000 1.0000000 0.6211356 1.0000000 1.0559050
## Mytilina.sp Lec.monostyla Lec.ligona Ascomorpha.sp Pom.sulcata Harpacticoida
## 1.1095267 0.9428530 1.0000000 1.0000000 1.0000000 1.0000000
## Epi.senta Rot.neptunia Dis.aculeata Lec.luna Euc.dilatata Bea.eudactylota
## 1.0000000 0.6081734 1.2962445 1.0000000 1.0000000 0.0000000
## Chy.sphaericus Lec.hornemanni Dia.birgei Mac.subquadratus Bra.quadridentatus Pol.vulgaris
## 0.2467517 0.0000000 0.3333333 0.0000000 0.0000000 0.0000000
## Pol.bicerca Dicranop.sp Asc.saltans Moi.minuta Alo.hamulata Mac.laticornis
## 0.0000000 0.0000000 0.0000000 0.0000000 0.5000000 0.0000000
## Mac.mira Pro.similis Alo.pulchella Dia.spinulosum Chydorus.sp Ily.spinifer
## 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 1.0000000
## Dun.odontoplax
## 1.0000000
## [1] "Bea.eudactylota" "Lec.hornemanni" "Mac.subquadratus" "Bra.quadridentatus" "Pol.vulgaris"
## [6] "Pol.bicerca" "Dicranop.sp" "Asc.saltans" "Moi.minuta" "Mac.laticornis"
## [11] "Mac.mira" "Pro.similis" "Alo.pulchella" "Dia.spinulosum" "Chydorus.sp"
## 'data.frame': 45 obs. of 70 variables:
## $ Bra.angularis : num 0 0.369 0.369 0 0 ...
## $ Lepadella.sp : num 0 0.0786 0.0786 0.1368 0.0786 ...
## $ Lecane.sp : num 0 0 0 0 0 ...
## $ Lec.leontina : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.bulla : num 0.0589 0 0.034 0.0538 0.024 ...
## $ Lec.cornuta : num 0 0 0 0 0 ...
## $ Lec.curvicornis : num 0 0 0 0 0 ...
## $ Notholca.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.urceolaris : num 0.392 0 0 0 0 ...
## $ Trichocerca.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.quadridentata: num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.kluchor : num 0.247 0 0 0 0 ...
## $ Lec.lunaris : num 0.1179 0.1677 0.2066 0 0.0831 ...
## $ Rotaria.sp : num 0 0.0765 0 0 0 ...
## $ Aspelta.sp : num 0.195 0 0 0 0 ...
## $ Lec.furcata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Col.geophila : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.dactyliseta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.calyciflorus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.caudatus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.crepida : num 0 0 0 0 0 ...
## $ Pla.patulus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.ovalis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.elasma : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Pla.quadricornis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.aculeata : num 0.442 0.316 0 0.137 0 ...
## $ Ker.tropica : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bdelloidea : num 0 0 0 0 0 ...
## $ Ker.lenzi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Con.unicornis : num 0 0 0 0 0 ...
## $ Alo.dadayi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Macrothrix.sp : num 0.195 0 0 0 0 ...
## $ Alonella.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Nauplii : num 0.0351 0.0393 0.0175 0.0393 0.0351 ...
## $ Chy.eurynotus : num 0.333 0 0 0 0 ...
## $ Cyclopoida : num 0 0 0 0 0 ...
## $ Mac.collinsi : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Copepodite : num 0 0 0 0.0557 0 ...
## $ Paracyclops.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Asc.ecaudis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.ovalis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Polyarthra.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.havanaensis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Hexarthra.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.hastata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Tri.tetractis : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ker.serrulata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Notodiaptomus.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Bra.falcatus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Fil.longiseta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Myt.crassipes : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lep.patella : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Euchlanis.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Colurella.sp : num 0 0 0.0963 0 0 ...
## $ Mytilina.sp : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.monostyla : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.ligona : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ascomorpha.sp : num 1 0 0 0 0 0 0 0 0 0 ...
## $ Pom.sulcata : num 0 0 0 0.5 0.5 0 0 0 0 0 ...
## $ Harpacticoida : num 0 0 0 0 0 0 0 1 0 0 ...
## $ Epi.senta : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Rot.neptunia : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dis.aculeata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Lec.luna : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Euc.dilatata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Chy.sphaericus : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dia.birgei : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Alo.hamulata : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Ily.spinifer : num 0 0 0 0 0 0 0 0 0 0 ...
## $ Dun.odontoplax : num 0 0 0 0 0 0 0 0 0 0 ...
## Bra.angularis Lepadella.sp Lecane.sp Lec.leontina Lec.bulla Lec.cornuta
## 1.3118631 2.2390217 1.0000000 1.0715261 2.0514645 1.1031787
## Lec.curvicornis Notholca.sp Bra.urceolaris Trichocerca.sp Lec.quadridentata Lec.kluchor
## 0.6306022 1.0000000 1.1754797 1.3906576 1.4326938 1.3068915
## Lec.lunaris Rotaria.sp Aspelta.sp Lec.furcata Col.geophila Lep.dactyliseta
## 2.1090000 2.1050221 1.4090954 0.3743807 1.0000000 1.0825147
## Bra.calyciflorus Bra.caudatus Lec.crepida Pla.patulus Lec.ovalis Lec.elasma
## 1.0000000 1.0000000 1.3125056 0.3698601 1.1754797 1.0000000
## Pla.quadricornis Lec.aculeata Ker.tropica Bdelloidea Ker.lenzi Con.unicornis
## 1.0000000 1.5132892 1.0000000 2.6638819 1.1666667 1.1595470
## Alo.dadayi Macrothrix.sp Alonella.sp Nauplii Chy.eurynotus Cyclopoida
## 1.4261054 0.3899645 1.2767999 1.9045455 1.5868805 1.4321709
## Mac.collinsi Copepodite Paracyclops.sp Asc.ecaudis Lep.ovalis Polyarthra.sp
## 1.0000000 1.9923047 1.0000000 1.0000000 1.5714360 1.0000000
## Bra.havanaensis Hexarthra.sp Lec.hastata Tri.tetractis Ker.serrulata Notodiaptomus.sp
## 1.0000000 1.0000000 0.2048328 0.4979181 1.0000000 1.0000000
## Bra.falcatus Fil.longiseta Myt.crassipes Lep.patella Euchlanis.sp Colurella.sp
## 0.2132229 1.0000000 1.0000000 0.6211356 1.0000000 1.0559050
## Mytilina.sp Lec.monostyla Lec.ligona Ascomorpha.sp Pom.sulcata Harpacticoida
## 1.1095267 0.9428530 1.0000000 1.0000000 1.0000000 1.0000000
## Epi.senta Rot.neptunia Dis.aculeata Lec.luna Euc.dilatata Chy.sphaericus
## 1.0000000 0.6081734 1.2962445 1.0000000 1.0000000 0.2467517
## Dia.birgei Alo.hamulata Ily.spinifer Dun.odontoplax
## 0.3333333 0.5000000 1.0000000 1.0000000
## Bra.angularis Lepadella.sp Lecane.sp Lec.leontina Lec.bulla Lec.cornuta Lec.curvicornis Notholca.sp
## BB1-P01 0.0000000 0.00000000 0.0000000 0.0000000 0.05893968 0.0000000 0.0000000 0
## BB1-P02 0.3690101 0.07856172 0.0000000 0.0000000 0.00000000 0.0000000 0.0000000 0
## BB1-P03 0.3690101 0.07856172 0.0000000 0.0000000 0.03399641 0.0000000 0.0000000 0
## BB2-P01 0.0000000 0.13677765 0.0000000 0.0000000 0.05379148 0.0000000 0.0000000 0
## BB2-P02 0.0000000 0.07856172 0.0000000 0.0000000 0.02403337 0.0000000 0.0000000 0
## BB2-P03 0.0000000 0.07856172 0.0000000 0.0000000 0.00000000 0.0000000 0.0000000 0
## BB3-P01 0.0000000 0.00000000 0.3333333 0.0000000 0.04164684 0.1131341 0.0000000 0
## BB3-P02 0.0000000 0.00000000 0.0000000 0.0000000 0.07223791 0.0000000 0.0000000 0
## BB3-P03 0.0000000 0.00000000 0.0000000 0.0000000 0.06809025 0.1131341 0.0000000 0
## BB4-P01 0.0000000 0.00000000 0.0000000 0.0000000 0.06809025 0.0000000 0.1473631 0
## BB4-P02 0.0000000 0.00000000 0.0000000 0.0000000 0.03399641 0.0000000 0.0000000 1
## BB4-P03 0.0000000 0.00000000 0.0000000 0.0000000 0.05893968 0.0000000 0.0000000 0
## BB5-P01 0.0000000 0.00000000 0.0000000 0.0000000 0.08347325 0.0000000 0.0000000 0
## BB5-P02 0.0000000 0.07856172 0.0000000 0.1949822 0.04810108 0.1131341 0.0000000 0
## Bra.urceolaris Trichocerca.sp Lec.quadridentata Lec.kluchor Lec.lunaris Rotaria.sp Aspelta.sp Lec.furcata
## BB1-P01 0.3918266 0 0.0000000 0.2467517 0.11788372 0.00000000 0.1949822 0
## BB1-P02 0.0000000 0 0.0000000 0.0000000 0.16769424 0.07645609 0.0000000 0
## BB1-P03 0.0000000 0 0.0000000 0.0000000 0.20662441 0.00000000 0.0000000 0
## BB2-P01 0.0000000 0 0.0000000 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB2-P02 0.0000000 0 0.0000000 0.0000000 0.08311677 0.00000000 0.0000000 0
## BB2-P03 0.0000000 0 0.0000000 0.0000000 0.08311677 0.00000000 0.0000000 0
## BB3-P01 0.0000000 0 0.0000000 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB3-P02 0.0000000 0 0.0000000 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB3-P03 0.0000000 0 0.0000000 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB4-P01 0.0000000 0 0.0000000 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB4-P02 0.0000000 0 0.0000000 0.0000000 0.00000000 0.04407110 0.0000000 0
## BB4-P03 0.0000000 0 0.0000000 0.0000000 0.00000000 0.03115052 0.0000000 0
## BB5-P01 0.0000000 0 0.0000000 0.0000000 0.00000000 0.00000000 0.0000000 0
## BB5-P02 0.0000000 0 0.2163469 0.0000000 0.00000000 0.03115052 0.0000000 0
## Col.geophila Lep.dactyliseta Bra.calyciflorus Bra.caudatus Lec.crepida Pla.patulus Lec.ovalis Lec.elasma
## BB1-P01 0 0 0 0 0.0000000 0 0 0
## BB1-P02 0 0 0 0 0.0000000 0 0 0
## BB1-P03 0 0 0 0 0.0000000 0 0 0
## BB2-P01 0 0 0 0 0.0000000 0 0 0
## BB2-P02 0 0 0 0 0.0000000 0 0 0
## BB2-P03 0 0 0 0 0.2163469 0 0 0
## BB3-P01 0 0 0 0 0.0000000 0 0 0
## BB3-P02 0 0 0 0 0.0000000 0 0 0
## BB3-P03 0 0 0 0 0.0000000 0 0 0
## BB4-P01 0 0 0 0 0.0000000 0 0 0
## BB4-P02 0 0 0 0 0.0000000 0 0 0
## BB4-P03 0 0 0 0 0.0000000 0 0 0
## BB5-P01 0 0 0 0 0.0000000 0 0 0
## BB5-P02 0 0 0 0 0.0000000 0 0 0
## Pla.quadricornis Lec.aculeata Ker.tropica Bdelloidea Ker.lenzi Con.unicornis Alo.dadayi Macrothrix.sp
## BB1-P01 0 0.4418018 0 0.00000000 0 0.0000000 0 0.1949822
## BB1-P02 0 0.3163570 0 0.00000000 0 0.0000000 0 0.0000000
## BB1-P03 0 0.0000000 0 0.00000000 0 0.0000000 0 0.0000000
## BB2-P01 0 0.1367777 0 0.00000000 0 0.0000000 0 0.0000000
## BB2-P02 0 0.0000000 0 0.00000000 0 0.0000000 0 0.0000000
## BB2-P03 0 0.0000000 0 0.00000000 0 0.0000000 0 0.0000000
## BB3-P01 0 0.0000000 0 0.03451711 0 0.0000000 0 0.0000000
## BB3-P02 0 0.0000000 0 0.04883854 0 0.5000000 0 0.0000000
## BB3-P03 0 0.0000000 0 0.06913621 0 0.3918266 0 0.0000000
## BB4-P01 0 0.0000000 0 0.15584137 0 0.0000000 0 0.0000000
## BB4-P02 0 0.0000000 0 0.09159462 0 0.0000000 0 0.0000000
## BB4-P03 0 0.0000000 0 0.07733485 0 0.0000000 0 0.0000000
## BB5-P01 0 0.0000000 0 0.18685187 0 0.0000000 0 0.0000000
## BB5-P02 0 0.0000000 0 0.13910507 0 0.0000000 0 0.0000000
## Alonella.sp Nauplii Chy.eurynotus Cyclopoida Mac.collinsi Copepodite Paracyclops.sp Asc.ecaudis Lep.ovalis
## BB1-P01 0.0000000 0.03510911 0.3333333 0.00000000 0 0.00000000 0 0 0
## BB1-P02 0.0000000 0.03925816 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB1-P03 0.0000000 0.01754788 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB2-P01 0.0000000 0.03925816 0.0000000 0.00000000 0 0.05569274 0 0 0
## BB2-P02 0.0000000 0.03510911 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB2-P03 0.0000000 0.02481960 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB3-P01 0.0000000 0.00000000 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB3-P02 0.0000000 0.02481960 0.0000000 0.09862661 0 0.05569274 0 0 0
## BB3-P03 0.0000000 0.02481960 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB4-P01 0.0000000 0.04967702 0.0000000 0.00000000 0 0.05569274 0 0 0
## BB4-P02 0.0000000 0.01754788 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB4-P03 0.0000000 0.01754788 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB5-P01 0.2163469 0.03724120 0.0000000 0.00000000 0 0.00000000 0 0 0
## BB5-P02 0.1232867 0.04301063 0.2300535 0.00000000 0 0.07886254 0 0 0
## Polyarthra.sp Bra.havanaensis Hexarthra.sp Lec.hastata Tri.tetractis Ker.serrulata Notodiaptomus.sp Bra.falcatus
## BB1-P01 0 0 0 0 0 0 0 0
## BB1-P02 0 0 0 0 0 0 0 0
## BB1-P03 0 0 0 0 0 0 0 0
## BB2-P01 0 0 0 0 0 0 0 0
## BB2-P02 0 0 0 0 0 0 0 0
## BB2-P03 0 0 0 0 0 0 0 0
## BB3-P01 0 0 0 0 0 0 0 0
## BB3-P02 0 0 0 0 0 0 0 0
## BB3-P03 0 0 0 0 0 0 0 0
## BB4-P01 0 0 0 0 0 0 0 0
## BB4-P02 0 0 0 0 0 0 0 0
## BB4-P03 0 0 0 0 0 0 0 0
## BB5-P01 0 0 0 0 0 0 0 0
## BB5-P02 0 0 0 0 0 0 0 0
## Fil.longiseta Myt.crassipes Lep.patella Euchlanis.sp Colurella.sp Mytilina.sp Lec.monostyla Lec.ligona
## BB1-P01 0 0 0 0 0.00000000 0.0000000 0 0
## BB1-P02 0 0 0 0 0.00000000 0.0000000 0 0
## BB1-P03 0 0 0 0 0.09634135 0.0000000 0 0
## BB2-P01 0 0 0 0 0.00000000 0.0000000 0 0
## BB2-P02 0 0 0 0 0.00000000 0.0000000 0 0
## BB2-P03 0 0 0 0 0.00000000 0.0000000 0 0
## BB3-P01 0 0 0 0 0.00000000 0.0000000 0 0
## BB3-P02 0 0 0 0 0.00000000 0.0000000 0 0
## BB3-P03 0 0 0 0 0.00000000 0.0000000 0 0
## BB4-P01 0 0 0 0 0.00000000 0.0000000 0 0
## BB4-P02 0 0 0 0 0.00000000 0.0000000 0 0
## BB4-P03 0 0 0 0 0.00000000 0.0000000 0 0
## BB5-P01 0 0 0 0 0.00000000 0.0000000 0 0
## BB5-P02 0 0 0 0 0.00000000 0.1949822 0 0
## Ascomorpha.sp Pom.sulcata Harpacticoida Epi.senta Rot.neptunia Dis.aculeata Lec.luna Euc.dilatata Chy.sphaericus
## BB1-P01 1 0.0 0 0 0 0 0 0 0
## BB1-P02 0 0.0 0 0 0 0 0 0 0
## BB1-P03 0 0.0 0 0 0 0 0 0 0
## BB2-P01 0 0.5 0 0 0 0 0 0 0
## BB2-P02 0 0.5 0 0 0 0 0 0 0
## BB2-P03 0 0.0 0 0 0 0 0 0 0
## BB3-P01 0 0.0 0 0 0 0 0 0 0
## BB3-P02 0 0.0 1 0 0 0 0 0 0
## BB3-P03 0 0.0 0 0 0 0 0 0 0
## BB4-P01 0 0.0 0 0 0 0 0 0 0
## BB4-P02 0 0.0 0 1 0 0 0 0 0
## BB4-P03 0 0.0 0 0 0 0 0 0 0
## BB5-P01 0 0.0 0 0 0 0 0 0 0
## BB5-P02 0 0.0 0 0 0 0 0 0 0
## Dia.birgei Alo.hamulata Ily.spinifer Dun.odontoplax
## BB1-P01 0 0 0 0
## BB1-P02 0 0 0 0
## BB1-P03 0 0 0 0
## BB2-P01 0 0 0 0
## BB2-P02 0 0 0 0
## BB2-P03 0 0 0 0
## BB3-P01 0 0 0 0
## BB3-P02 0 0 0 0
## BB3-P03 0 0 0 0
## BB4-P01 0 0 0 0
## BB4-P02 0 0 0 0
## BB4-P03 0 0 0 0
## BB5-P01 0 0 0 0
## BB5-P02 0 0 0 0
## [ reached 'max' / getOption("max.print") -- omitted 31 rows ]
## [1] 31504.13 Exportando a matriz particionada
write.table(m_part,
"m_parttxt.txt",
sep = "\t",
quote = FALSE)
write.table(m_part,
"m_partcsv.csv",
append = F,
quote = TRUE, sep = ";",
dec = ",",
row.names = T)
#shell.exec(dir) #abre o diretorio de trabalho no Windows Explorer
m_part_csv <- read.csv("m_partcsv.csv",
sep = ";",
dec = ",",
header = T,
row.names = 1,
na.strings = NA)## Análise de Classificação - SAHN
system(paste("open", shQuote("D:/Elvio/OneDrive/MSS/_Zoo-Rebio/R_ZooRebio/sahn.qmd")))Apêndices
Relativizações
4.13.0.1 Total das colunas
m_relcol <- decostand(m_bruta,
method="total",
MARGIN = 2)
View(m_relcol)
m_relcolA função decostand() é usada para relativizar os dados. O parâmetro method especifica o método de relativização, neste caso “total” (relativização pelo total de cada coluna). Outros métodos disponíveis são max, normalize, range e rankm (Figura 4.1). O parâmetro MARGIN especifica em qual dimensão os cálculos devem ser feitos (1 para linhas, 2 para colunas). Neste caso, MARGIN=2 (colunas). A variável m_relcol armazena o resultado da relativização. Sokal e Rohlf (1995) tratam dos diversos tipos de relativizações e transformações em dados ecológicos.
| Função | Descrição | Uso adequado |
|---|---|---|
| max | Divide cada valor pela maior observação da coluna em que está localizado. Todos os valores resultantes serão menores ou iguais a 1. Adequada para análise em escala relativa | Quando a escala de cada variável é conhecida e a análise deve ser feita em uma escala relativa |
| normalize | Divide cada valor pelo comprimento do vetor. Isso resulta em valores cujo comprimento é sempre igual a 1. Adequada para análise de dados de frequência | Para análise de dados de frequência |
| range | Subtrai o valor mínimo da coluna de cada valor e, em seguida, divide pelo intervalo (ou amplitude) dos valores da coluna. Isso resulta em valores entre 0 e 1. | Quando a amplitude dos valores em cada coluna é importante para a análise |
| rankm | Transforma os valores em suas posições dentro da coluna, em ordem crescente. O menor valor recebe o valor 1 e o maior valor recebe o valor igual ao comprimento da coluna. | Quando a escala absoluta dos valores não é importante, mas a ordem dos valores é significativa. |
Transformações
Essa seção realiza diversas transformações nos dados. Para cada transformação, a função é aplicada aos dados da matriz e o resultado é armazenado em uma nova variável. A função View() é usada para visualizar o resultado de cada transformação na forma de uma tabela. Ela mostra o código que realiza diversas transformações na matriz de dados. Para cada transformação, a função é aplicada aos dados e o resultado é armazenado em uma nova variável.
Log10
Não aceita zeros, porque o log de zero é indeterminado. Por isso devemos substituir os valores com erro (infinito negativo) por zero, usando a função replace().
m_lg10 <- log10(m_bruta)
View(m_lg10)
m_lg10 <- replace(m_lg10, is.infinite(m_lg10), 0)
head(m_lg10)Exponenciais
“Power transformations”, onde o valor de p estabelece a compressão dos dados.
m_bruta_P1 <- m_bruta^1 #p=1
View(m_bruta_P1)
m_bruta_P05 <- m_bruta^0.5 #p=0,5
View(m_bruta_P05)
m_bruta_P01 <- m_bruta^0.1 #p=0,1
View(m_bruta_P01)Arcoseno da raiz quadrada
Os valores de entrada tem que variar entre 0 e 1. Ideal para matrizes relativizadas. Duas formulações estão disponíveis, com e sem a multiplicação por 2/pi. A segunda opção costuma ter melhor efeito na normalização dos dados.
m_asrq <- asin(sqrt(m_relcol))
View(m_asrq)
m_asrqpi <- 2/pi*(asin(sqrt(m_relcol)))
View(m_asrqpi)