Regresión lineal simple

Introducción

Muchos de los aspectos teóricos serán explicados en la clase utilizando la siguiente presentación. Aquí nos centramos en como realizar una regresión lineal en R.

Existe e evidencia suficiente para conocer que el consumo de sal tiene efectos sobre la tensión arterial. A mayor consumo de sal se observan mayores niveles de tensión arterial. Un análisis de regresión lineal, entre otras cosas, permite cuantificar la relación entre dos variables. En este caso, se pretende cuantificar la relación entre el consumo de sal y la tensión arterial. Es decir, mediante un análisis de regresión lineal se puede establecer una relación matemática entre el consumo de sal y la tensión arterial y describir como cambian un variable en función de la otra.

Las técnicas de regresión se utilizan para:

Predicción
Identificación de factores de riesgos
Para aislar el efecto de una sola variable
Para identificar el efecto de varias variables sobre una dependiente
Identificar la independencia de dos variables
Análisis de supervivencia

Las técnicas de regresión son una de las técnicas más maravillosas que existen. Por lo pronto nos enfocaremos en su versión más simple: la regresión lineal simple.

Regresión lineal simple

El análisis de regresión lineal simple es una técnica que se utiliza para explicar o modelar la relación entre dos variables numéricas. En esta técnica se debe diferenciar e identificar la variable dependiente (y) y la variable independiente o predictora (x). Vamos a poner en contexto a la regresión lineal utilizando el ejemplo de la relación entre el consumo de sal y la tensión arterial.

La base de datos sal.csv contiene información sobre el consumo de sal y la tensión arterial. La variable sal representa el consumo de sal en mg y la variable tension representa la tensión arterial en mmHg.

Su objetivo es conocer la relación de estas dos variables. Para ello, se ajustará un modelo de regresión lineal simple.

Importación de los datos

df <- read.csv(file = "Bases/sal_tension_arterial.csv")

Visaluación de los datos

Un punto importante antes de realizar una regresión es observar la relación que tienen los datos visualmente y medienta un coeficiente de correlación.

library(ggplot2)
df|>
  ggplot(mapping = aes(x=Consumo_Sal, y=Tension_Arterial))+
  geom_point(col= "cyan4", alpha = 0.8, size = 3)+
  theme_linedraw()+labs(x="Comsumo de sal", y= "mmHg")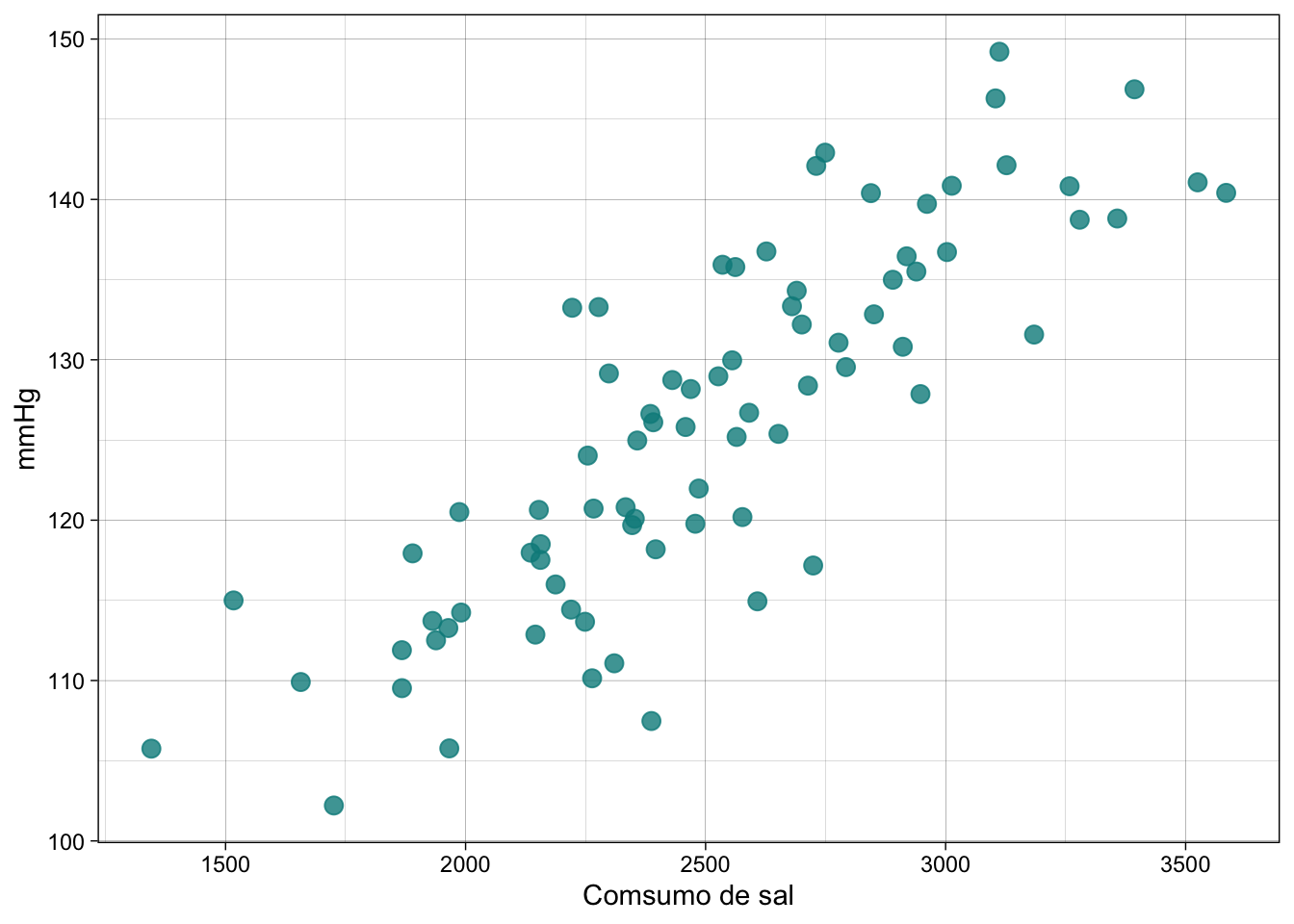

cor.test(df$Consumo_Sal, df$Tension_Arterial)


    Pearson's product-moment correlation

data:  df$Consumo_Sal and df$Tension_Arterial
t = 13.459, df = 78, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7550534 0.8919377
sample estimates:
      cor 
0.8360682

Creación del modelo de regresión

lm(Tension_Arterial~Consumo_Sal, data = df)|>
  summary()


Call:
lm(formula = Tension_Arterial ~ Consumo_Sal, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.989  -3.424  -0.313   3.531  13.142 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 74.839105   3.861251   19.38   <2e-16 ***
Consumo_Sal  0.020370   0.001513   13.46   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.213 on 78 degrees of freedom
Multiple R-squared:  0.699, Adjusted R-squared:  0.6952 
F-statistic: 181.1 on 1 and 78 DF,  p-value: < 2.2e-16

Lo primero que observamos en estos resultados es la ecuación de la recta: lm(formula = Tension_Arterial ~ Consumo_Sal, data = df). La interpretación de estos resultados requiere de la revisión de otros conceptos y de una descripción más detalla. De momento identifique el valor de 0.020370, el cual nos dice que por cada mg que se aumente el consumo de sal en una unidad, la tensión arterial aumenta en en promedio 0.020370 mmHg.

Interpretación de los resultados

Coeficientes \(\beta\)

En una regresión lineal simple hay dos coeficientes que son muy útiles para la interpretación correcta de los resultados. Estos dos valores son coeficientes \(\beta\) que son representados como \(\beta_1\) y \(\beta_0\) respectivamente.

Pendiente \(\beta_1\)

El coeficiente \(\beta_1\) es el valor que nos dice cuánto aumenta la variable dependiente por cada unidad que aumenta la variable independiente. En este caso, el coeficiente \(\beta_1\) es de 0.020370. Esto significa que por cada mg que se aumente el consumo de sal, la tensión arterial aumenta en promedio 0.020370 mmHg.

Intercepto

El intercepto \(\beta_0\) es valor en el que la linea de la regresión cruza el eje de las y. En otras palabras sería el valor de la presión arterial cuando el consumo de sal es cero, en este caso el intercepto es de 74.839105 mmHg. Tome en cuenta que esto no siempre tiene sentido.

Intervalos de confianza

lm(Tension_Arterial~Consumo_Sal, data = df)|>
  confint()

                  2.5 %      97.5 %
(Intercept) 67.15194384 82.52626615
Consumo_Sal  0.01735684  0.02338306

Para \(\beta_1\) los valores van de 0.017 a 0.023, no incluyen al 0. Por lo tanto podríamos asegurar que nuestro valor de \(\beta_1\) es diferente de 0 con un 95% de confianza.

Coeficiente de determinación

Pata este modelo \(R^2\) fue 0.699 (se puede obtener mediante summary), lo que significa que aproximadamente el 69.9% de la variabilidad en la tensión arterial puede ser explicada por el consumo de sal. El \(R^2\) puede tomar valores de 0 a 1

ANOVA

El ANOVA determina si existe una relación lineal significativa entre las variables independientes y la variable dependiente. La \(H_0\) para este ANOVA es que todos los coeficientes de regresión (excepto el intercepto) son iguales a cero

Se obtiene mediante summary

Evaluación de los supuestos

La regresión requiere para ser válida ciertos supuestos.

Normalidad de los residuos

En una regresión lineal, aunque sería ideal, no es necesario que los datos sigan una distribución normal. Lo que se requiere es que los residuos sigan una distribución normal. Esta normalidad se puede evaluar gráficamente, en el propio modelo de regresión y mediante pruebas estadísticas.

lm(Tension_Arterial~Consumo_Sal, data = df)|>
  summary()


Call:
lm(formula = Tension_Arterial ~ Consumo_Sal, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.989  -3.424  -0.313   3.531  13.142 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 74.839105   3.861251   19.38   <2e-16 ***
Consumo_Sal  0.020370   0.001513   13.46   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.213 on 78 degrees of freedom
Multiple R-squared:  0.699, Adjusted R-squared:  0.6952 
F-statistic: 181.1 on 1 and 78 DF,  p-value: < 2.2e-16

modelo <- lm(Tension_Arterial~Consumo_Sal, data = df)
nortest::lillie.test(modelo$residuals)


    Lilliefors (Kolmogorov-Smirnov) normality test

data:  modelo$residuals
D = 0.061958, p-value = 0.6297

library(ggrain)

Registered S3 methods overwritten by 'ggpp':
  method                  from   
  heightDetails.titleGrob ggplot2
  widthDetails.titleGrob  ggplot2

ggplot(mapping = aes(x=1, y=modelo$residuals))+
  geom_rain(fill="cyan4", alpha=0.5, col="black" )+
  theme_light()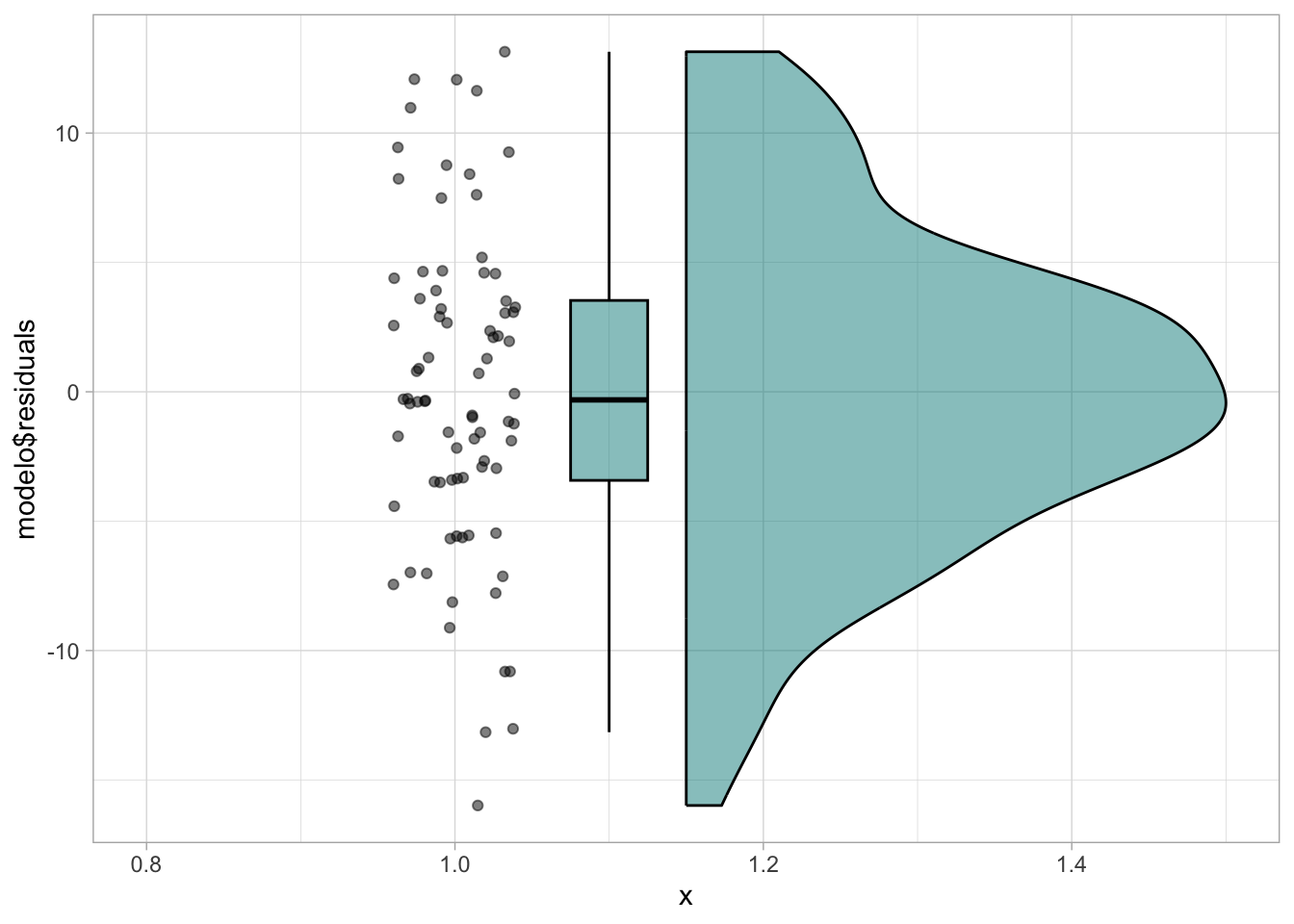

Evaluación gráfica de los modelos

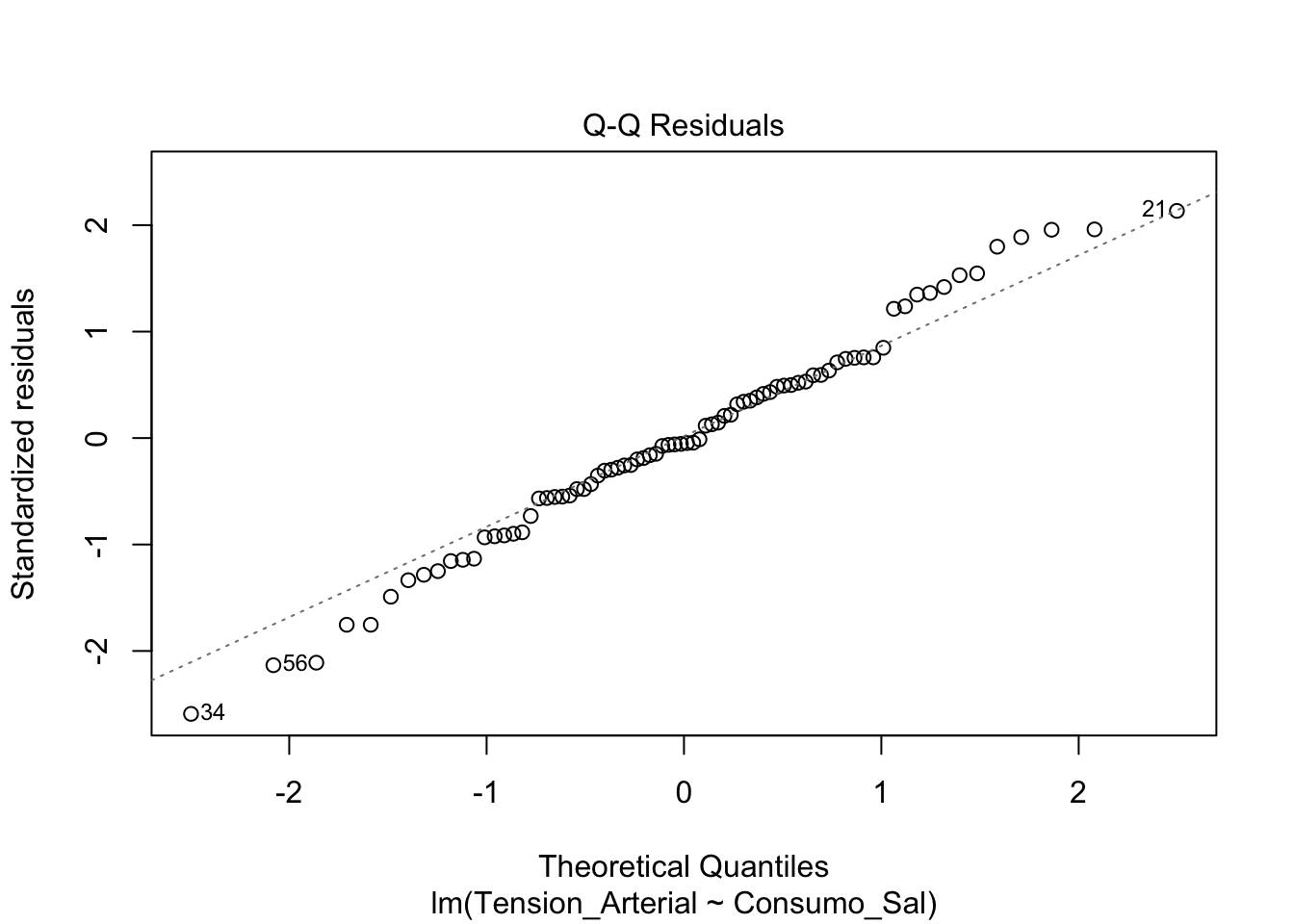
Necesitamos evaluar gráficamente los supuestos de la regresión lineal. Para ello, podemos utilizar los siguientes gráficos:

Gráfico de Residuos vs. Valores Ajustados: Permite evaluar la homoscedasticidad de las varianzas
Gráfico Q-Q de Residuos: Permite evaluar la normalidad de los residuos
Gráfico de Escala-Localización (Spread-Location Plot): Para evluar homoscedasticidad de las varianzas
Residuos vs Leverage: Indentificación de valore atípicos

Estos gráficos se pueden obtener mediante la función plot del modelo de regresión y luego dar enter.

plot(modelo)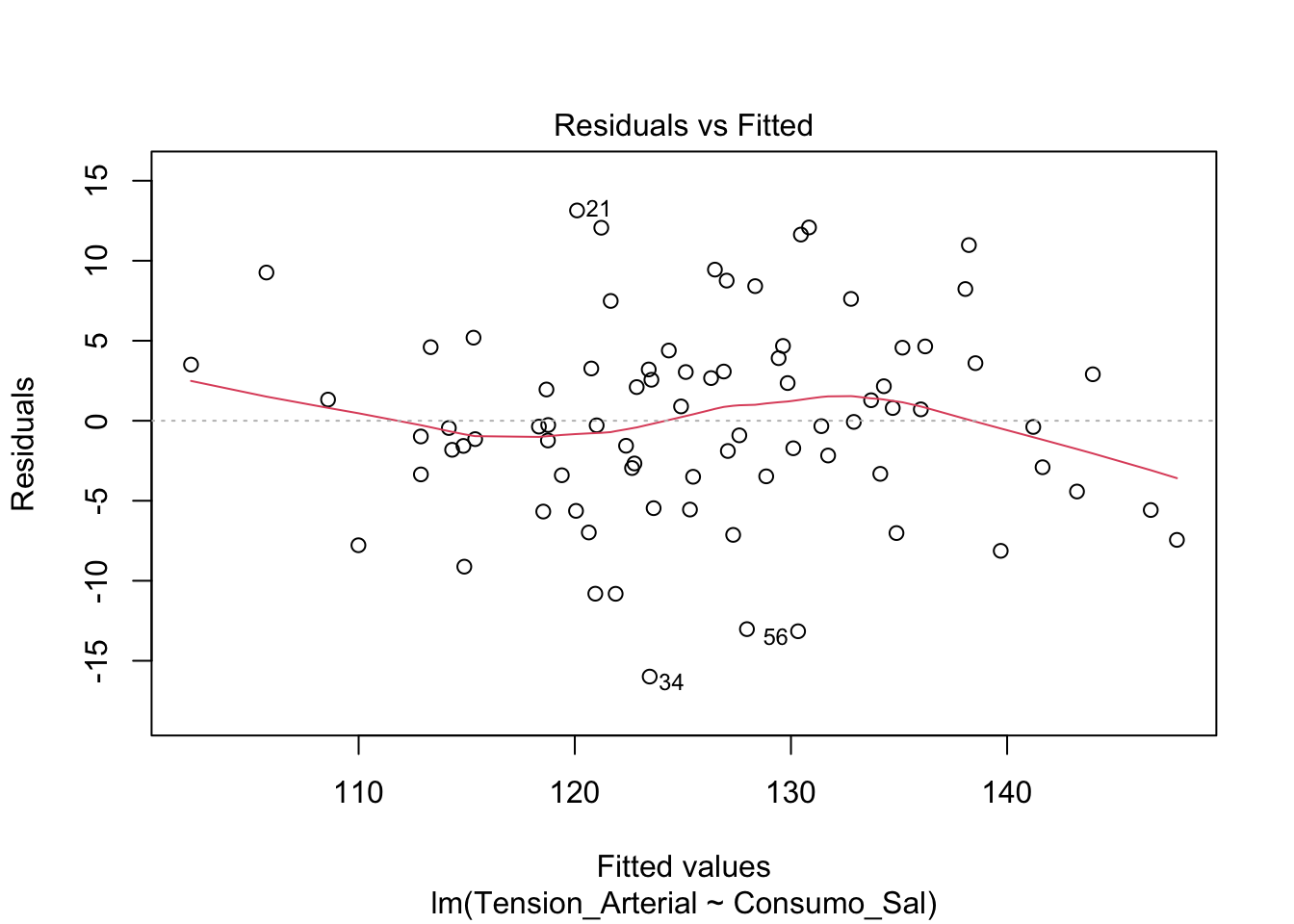

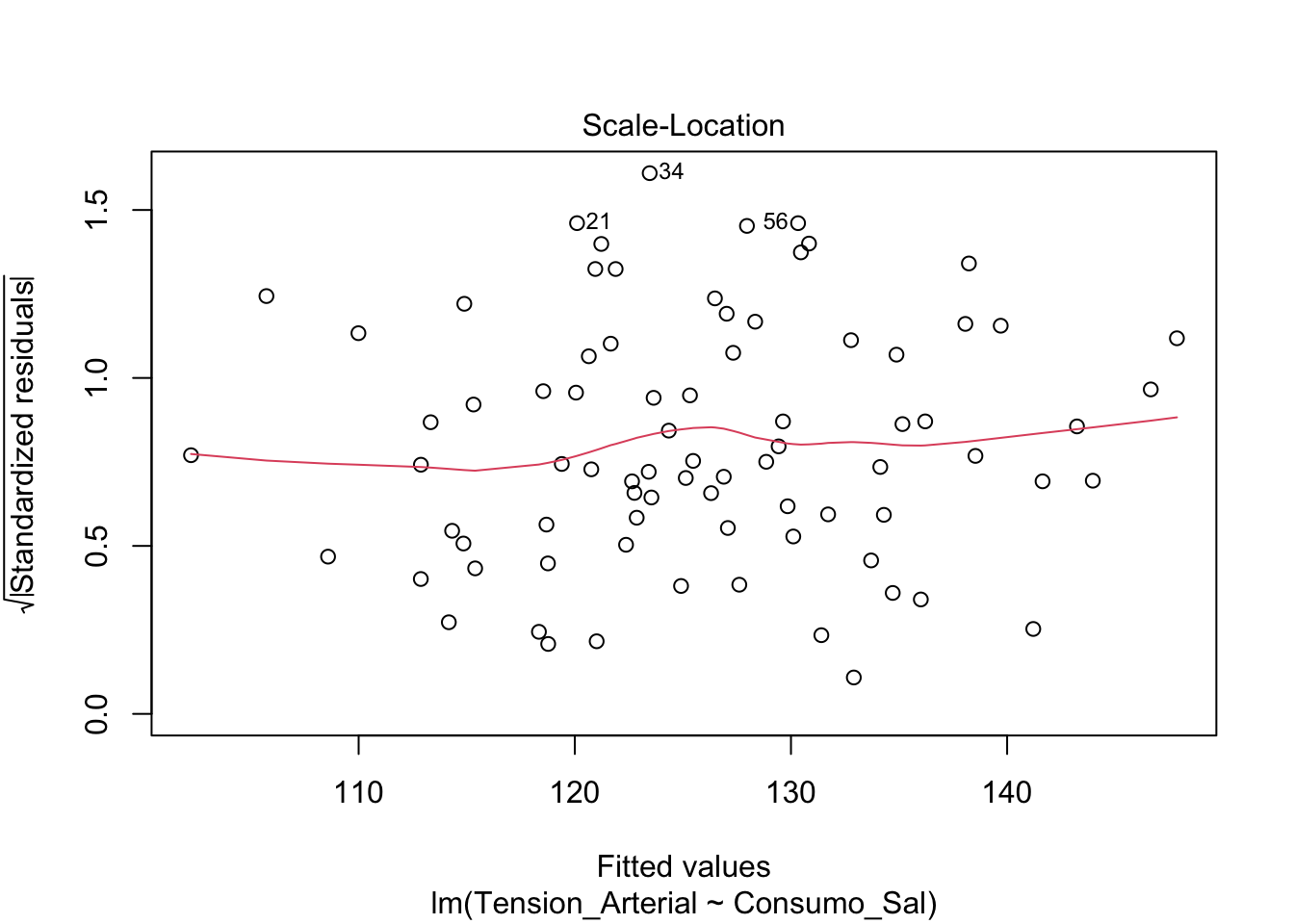
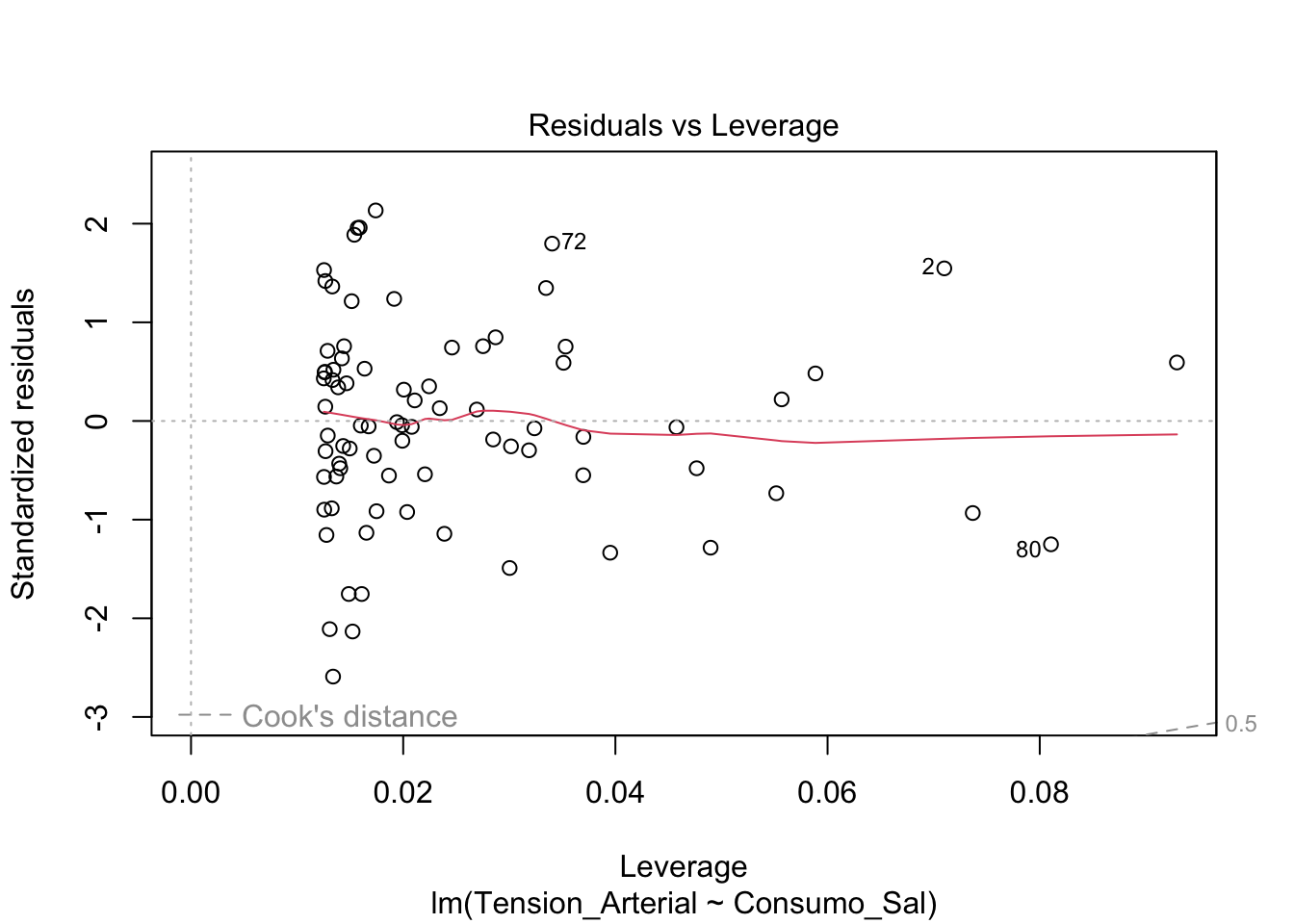
Uitlizando el perfromance también podemos evaluar los supuestos del modelo.

performance::check_model(modelo)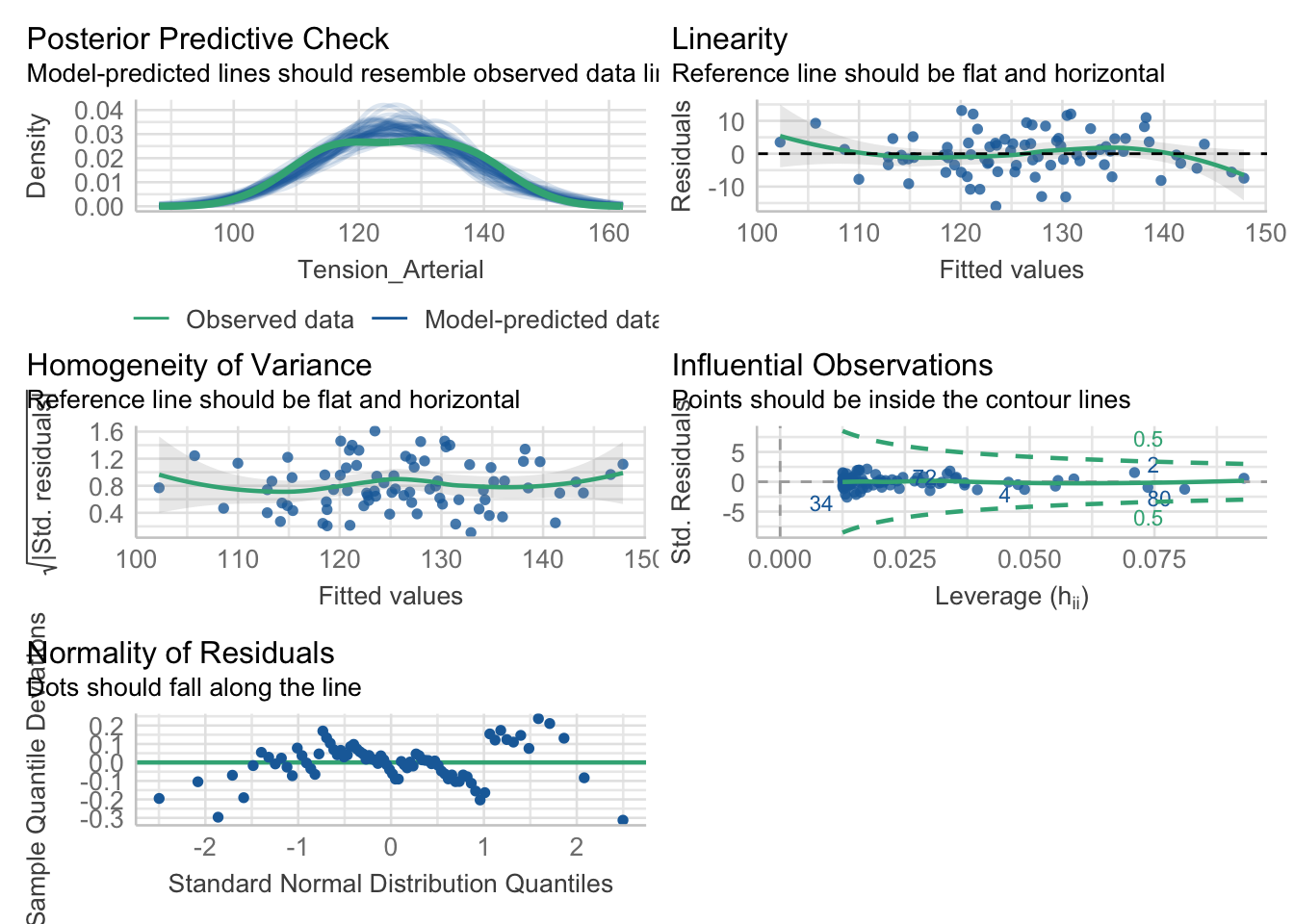

Resumen de los supuestos

Se hace una recopilación de los supuestos evaluados en el ejemplo de la regresión.

Linealidad: Debe de evidenciarse una relación lineal entre las variables antes realizar un modelo de regresión lineal

Utilice gráficos de dispersión
Coeficiente de correlación de Pearson

Independencia de los datos. Este concepto no se había explicado antes, sin embargo, es fácil de comprender. En una regresión las observaciones individuales no deben estar relacionadas o influenciadas entre sí.

Cuando se recolectan los datos debe de asegurarse la no relación de la variables, por ejemplo, no se debe de incluir mediciones repetidas del mismo sujeto • En los gráficos de residuales también se hace evidente esta relación

Homoscedasticidad: los residuos tienen varianza constante a lo largo de los valores predichos.

Utilice gráficos de diagnóstico para comprobar la homoscedasticidad.

Normalidad de los Residuos: los residuos del modelo deben de estar distribuidos normalmente.

Histogramas de los residuos.
Gráficos Q-Q de los residuos.
Pruebas de normalidad

Predicciones

Con una regresión podemos dado un dato de la variable independiente predecir el valor de la variable dependiente. Por ejemplo

predict(modelo, newdata = data.frame(Consumo_Sal = 10))

      1 
75.0428

Un mal ejemplo

Se desea comprobar la dependencia de la edad sobre la adiponectina. Construya un modelo de regresión lineal utilizando la base de datos SLE Dataset 3

library(readr)
SLE_dataset3 <- read_csv("Bases/SLE dataset3.csv")

Graficar

plot(SLE_dataset3$Adiponectin~ SLE_dataset3$Age, main="Concentraciones de adiponectina por edad")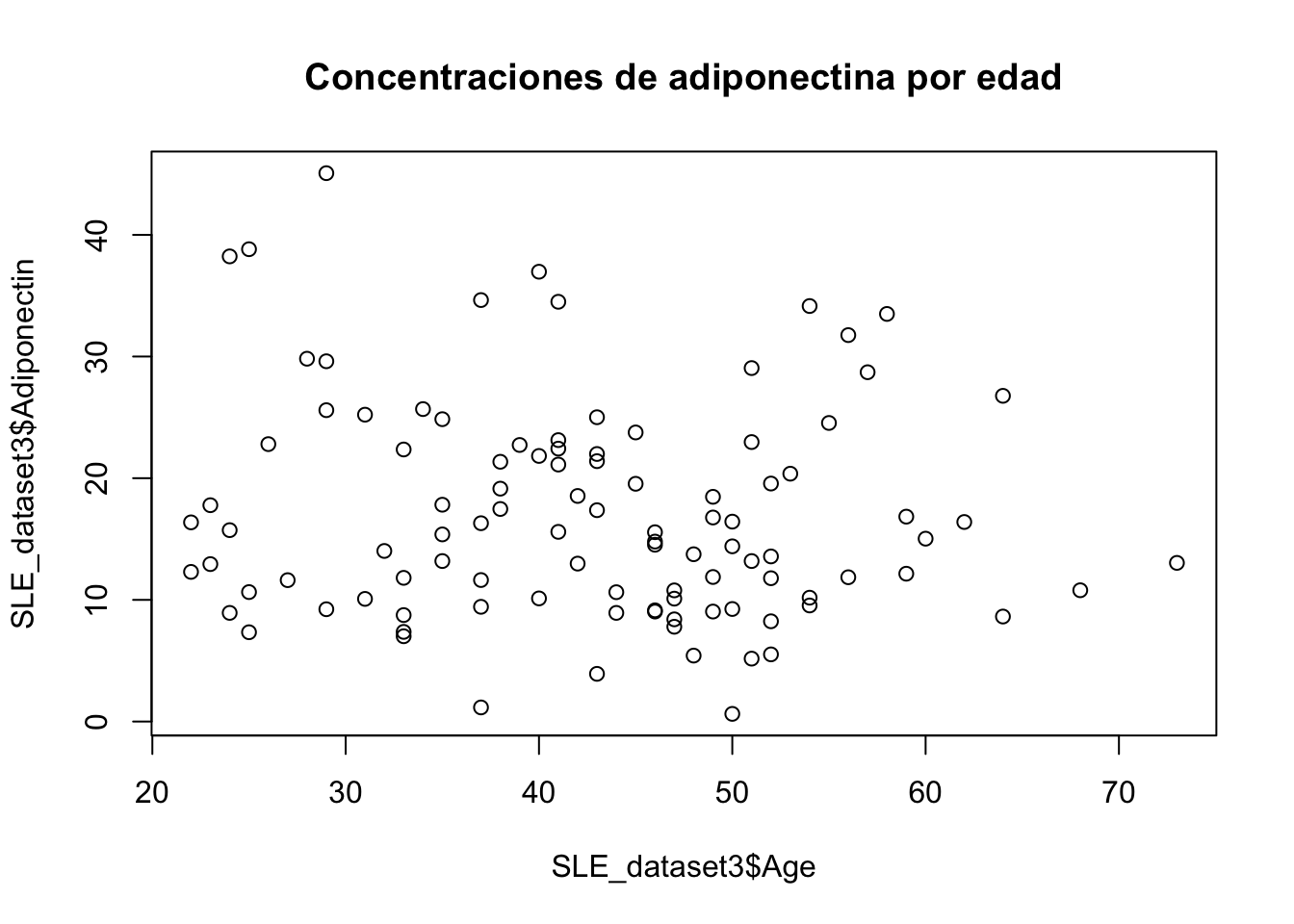

cor.test(SLE_dataset3$Adiponectin,SLE_dataset3$Age)


    Pearson's product-moment correlation

data:  SLE_dataset3$Adiponectin and SLE_dataset3$Age
t = -1.2614, df = 101, p-value = 0.2101
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.31057423  0.07069386
sample estimates:
       cor 
-0.1245346

Construir objeto

mod2 <- lm(SLE_dataset3$Adiponectin~ SLE_dataset3$Age)

Resultados del modelo

summary(mod2)


Call:
lm(formula = SLE_dataset3$Adiponectin ~ SLE_dataset3$Age)

Residuals:
    Min      1Q  Median      3Q     Max 
-16.372  -6.577  -1.860   4.818  26.754 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)      21.15562    3.41905   6.188 1.32e-08 ***
SLE_dataset3$Age -0.09792    0.07763  -1.261     0.21    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.832 on 101 degrees of freedom
Multiple R-squared:  0.01551,   Adjusted R-squared:  0.005761 
F-statistic: 1.591 on 1 and 101 DF,  p-value: 0.2101

Interpretación

La adiponectina es independiente de la edad. El ANOVA nos dice que el modelo no es adecuado ya que la variación de los residuales es muy alta
El coeficiente \(\beta_1\) no es siginifativo por lo tanto no podemos asegurar que sea distinto de cero

Validez del modelo

plot(mod2)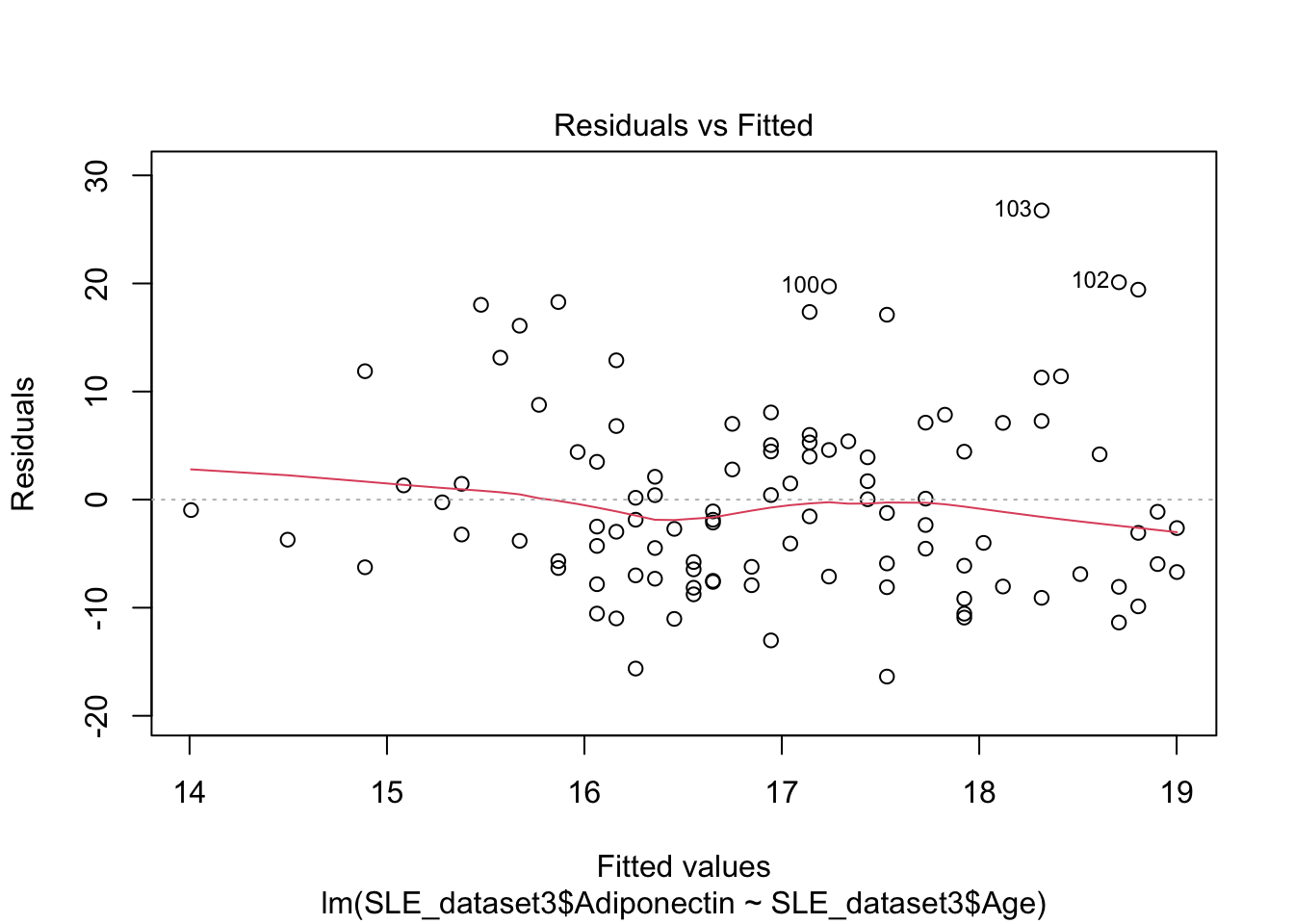

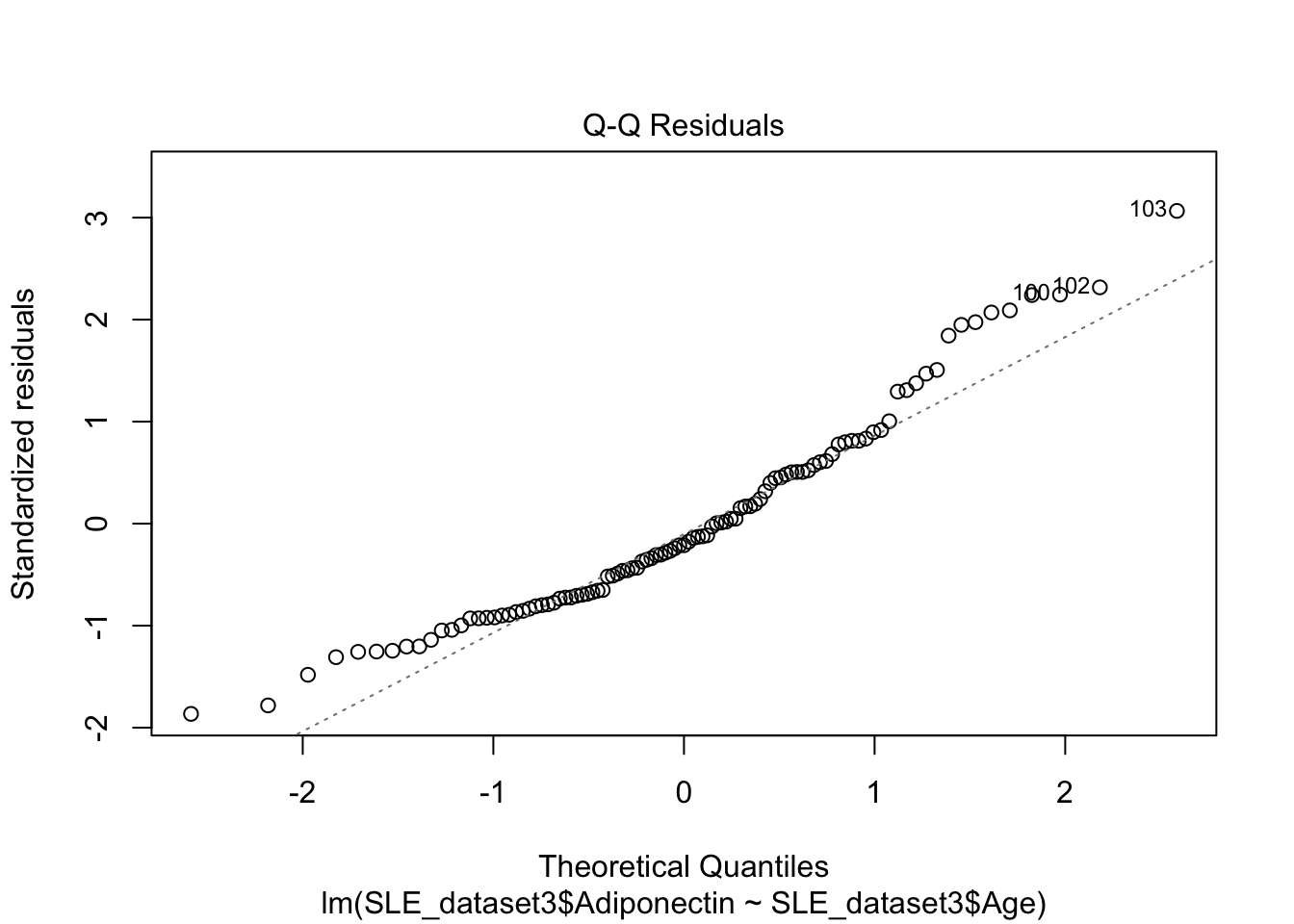
El gráfico Q-Q muestra que los residuos no se apegan a una distribución normal. Por tanto nuestro modelo no es valido.