Regresión logística

Aspectos teóricos

Edsaúl E. Pérez-Guerrero, PhD; edsaul.perezg@academicos.udg.mx

2024-11-20

Introducción

• La regresión logística es uno de los procedimientos estadísticos más utilizados en medicina
• Sigue muchos de los elementos comunes con la regresión múltiple
• Se utiliza cuando las variables dependientes son dicotómicas
• Algunos tipos son:
  • Regresión logística binaria
  • Regresión logística múltiple

Introducción

• La regresión logística se utiliza cuando se disponga de una variable dependiente dicotómica y se tengan uno o más predictores
• “Se usa la regresión logística binaria cuando se desea conocer el modo en que diversos factores (variables cuantitativas o categóricas) se asocian simultáneamente a una variable dependiente que es cualitativa (o categórica) dicotómica ¹

1. Fragmento de Bioestadística amigable (Spanish Edition) Miguel Ángel Martínez González.

El modelo de la regresión logística

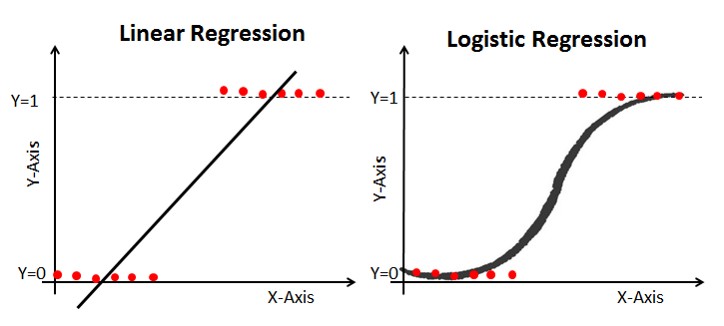
Regresion logistica vs lineal

El modelo de la regresión logística

La función logit

La función logit es una transformación matemática utilizada en la regresión logística para modelar relaciones entre variables. Se define como el logaritmo de las probabilidades (odds) de que ocurra un evento frente a que no ocurra. Matemáticamente, la función logit se expresa así:

[ (p) = () ]

donde: - ( p ) es la probabilidad de que ocurra el evento de interés (por ejemplo, que un paciente desarrolle una enfermedad), - ( ) es la razón de probabilidades (odds) de que el evento ocurra.

El modelo de la regresión logística

La primera aproximación y después de hacer una transformación que podemos tener de la regresión logística es:

\[In \bigg(\frac{p}{1-p} \bigg)= a + b_1x_1+b_2x_2+...+b_px_p\]

Las expresión \(y\) ahora es un expresión que no tiene sentido numérico por si sola. Esta expresión es un odds

\[Odss=\frac{p}{1-p}\]

El modelo de la regresión logística

La función logit

En la regresión logística, la función logit permite modelar la probabilidad de un evento como una función lineal de los predictores. Esto significa que, en vez de modelar directamente la probabilidad ( p ), se modela el logit(p) en una ecuación lineal con los predictores:

[ (p) = _0 + _1 x_1 + _2 x_2 + + _k x_k ]

donde ( _0, _1, , _k ) son los coeficientes del modelo y ( x_1, x_2, , x_k ) son los valores de los predictores.

¿Qué es un odds?

Es la cantidad de individuos con una características divido entre los que que no la presentan.

Supongamos que un estudio en el que se incluyeron 75 pacientes diagnosticados cáncer de próstata y tratados con un fármaco A. 50 pacientes presentaron remisión 25 fallaron a esta terapia.

¿Qué es un odds?

El odds para la respuesta sería:

\[Odds=\frac{50}{25}=2\] Con proporciones quedaría:

\[Odds=\frac{0.66}{1-0.66}=2\] Por cada paciente en el que no se alcanzó el éxito terapéutico, hay dos en los que sí se logró. Un odds toma valores de 0 al infinito

¿Qué es un Odds ratio?

Es el cociente de dos Odds. Puede traducirse como:

• razón de oportunidades
• razón de posibilidades
• oportunidad relativa
• razón de probabilidades o razón de productos cruzados
• razón de momios

¿Qué es un Odds ratio?

Ahora suponga que se tienen datos de otro tratamiento con 100 pacientes en los que el éxito se alcanzó en 40 pacientes. Por lo tanto el odds sería:

\[Odss=\frac{p}{1-p}\] \[Odds=\frac{40}{60}=0.67\]

¿Qué es un Odds ratio?

\[Odss=\frac{p}{1-p}\] \[Odds=\frac{40}{60}=0.67\] Con proporciones quedaría:

\[Odds=\frac{0.40}{1-0.40}=0.67\]

¿Qué es un Odds ratio?

\[OR=\frac{odds 1}{odds2}\]

\[OR=\frac{2}{0.67}=2.98\]

• Si el OR vale 3, se interpreta que el tratamiento A ofrece una ventaja terapéutica tres veces superior al tratamiento B

• Un OR de 3 indica que el grupo de interés tiene tres veces más probabilidades de presentar el evento en comparación con el grupo de referencia

• “Una OR de 3 se interpreta como una ventaja tres veces superior de una de las categorías”¹

1. Fragmento de Bioestadística amigable (Spanish Edition) Miguel Ángel Martínez González.

¿Qué es un Odds Ratio (OR)?

• La interpretación del OR siempre debe realizarse en el contexto del estudio, ya que es una medida relativa y no absoluta de asociación.

• La interpretación del OR puede variar según el diseño del estudio. En estudios de casos y controles, el OR se utiliza comúnmente para estimar la asociación entre exposición y resultado. En estudios transversales y en estudios de cohortes con regresión logística, el OR también puede ser útil, pero no debe interpretarse como un riesgo absoluto.

Ejemplo de interpretación de un Odds Ratio

• Supongamos que el OR para un accidente de tránsito entre bebedores en comparación con no bebedores es de 20.

• Esto significa que las probabilidades de sufrir un accidente de tránsito son 20 veces mayores en el grupo de bebedores en comparación con el de no bebedores. Es importante recordar que esto se refiere a la probabilidad relativa (odds) y no a una probabilidad absoluta o directa de accidente.

Ejemplo de interpretación de un Odds Ratio

• Interpretación en un estudio de casos y controles: En un diseño de casos y controles, donde ya se seleccionan personas con y sin el evento (accidente de tránsito), el OR representa la probabilidad de que los casos (personas que tuvieron un accidente) hayan sido bebedores en comparación con los controles (quienes no tuvieron un accidente). Aquí, el OR se usa para inferir una posible asociación entre la exposición (consumo de alcohol) y el evento (accidente de tránsito), pero no se debe confundir con el riesgo relativo (RR).

Nota importante

• El OR indica solo una asociación y no debe interpretarse como causalidad. .

¿Qué es un Odds ratio?

Algunas de las características del OR son:

• Si no hay relación entre el factor y la enfermedad, el valor de OR es estadísticamente igual a 1.

• Si el factor aumenta la probabilidad de padecer la enfermedad, el OR es mayor que 1

• Si el factor disminuye la probabilidad de padecer la enfermedad es menor que 1.

¿Qué es un Odds ratio?

Si se parte de una tabla de contingencia como la siguiente:

	Evento (+)	Evento (-)	Total
Expuestos (+)	a	b	a+b
Expuestos (-)	c	d	c+d
Total	a+c	b+d	a+b+c+d

\[OR= \frac{A*D}{B*C}\]

Modelo de regresión logística

• El modelo de regresión logística se basa en la siguiente función:

\(f(z)=\frac{1}{1+e^-z}\)

• Donde:
  • \(e\) denota la función exponencial
  • \(z\) es cualquier cantidad
• Con esta función cualquier valor que tome \(z\) se transformará entre 0 y 1

Modelo de regresión logística

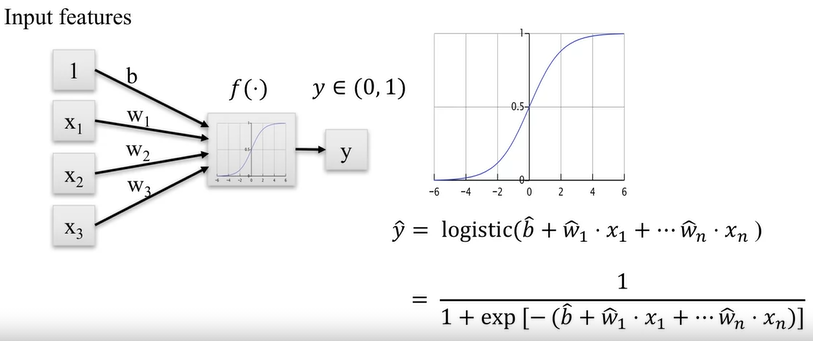
Modelo de regresión logística

• A partir de la función logística, obtenemos el modelo logístico mediante la sustitución \(z\) por \(\beta_0+\beta_1X_1+\beta_2X_2...\beta_kX_k\),

de modo que:

\(f(z)=\frac{1}{1+e^-z}=\frac{1}{1+e^{-(\beta_0+\beta_1X_1+\beta_2X_2...\beta_kX_k)}}\)

• Donde los coeficientes se estiman mediante el método de máxima verosimilitud (La idea es encontrar los valores de los coeficientes que maximicen la función de verosimilitud, es decir, que hagan que la probabilidad de observar los datos dados estos coeficientes sea lo más alta posible).
• Cuando estos coeficientes son conocidos, podemos, mediante el modelo logístico, calcular la probabilidad de que un individuo presente un evento de interés
• De hecho la regresión logística es un método que asigna probabilidades

Modelo de regresión logística

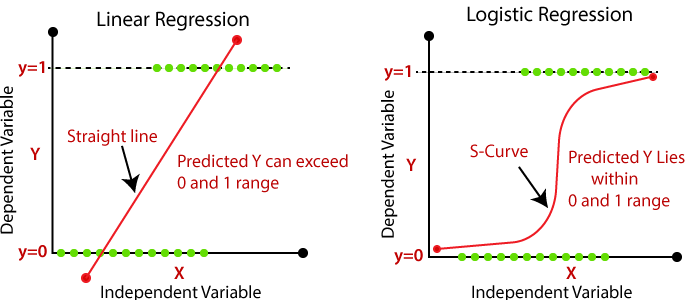
Coeficientes de regresión y OR

\[OR=\frac{ad}{cb}=\frac{(\frac{e^{\beta_0+\beta_{1}x_1}}{1+e^{\beta_0+\beta_1x1}})(\frac{1}{1+e^{\beta_0}})}{(\frac{e^{\beta_0}}{1+e^{\beta_0}})(\frac{1}{1+e^{\beta_0+\beta_1x1}})}=\frac{e^{\beta_0}+\beta1x1}{e^{\beta_0}}=e^{\beta_1}\]

Es posible obtener un valor de OR mediante el exponente de cada uno de los coeficientes. Esto es valido para estudios de casos y controles, transversales y estudios de cohorte.

Interpretación de los coeficientes de la regresión

“La interpretación más sencilla de la regresión logística es que cada coeficiente de regresión \(\beta_i\) expresa el logaritmo neperiano de la OR de que ocurra un fenómeno por unidad de cambio de esa variable independiente en cuestión.”¹

1. Fragmento de Bioestadística amigable (Spanish Edition) Miguel Ángel Martínez González.

Interpretación de los coeficientes de la regresión variables cualitativas

El OR para un accidente de tránsito entre bebedores y no bebedores es de 20. La interpretación sería:

• La odds de accidente tras haber bebido alcohol es 20 veces superior a la odds de accidente si no se ha bebido alcohol. Es la más exacta.

• El coeficiente expresa el logaritmo neperiano de la OR de que ocurra un fenómeno por unidad de cambio, de 0 a 1.

El riesgo de accidente entre los bebedores es de 20 comparado con los no bebedores. Interpretación en palabras comunes.

Interpretación de los coeficientes de la regresión variables cuantitativas

El OR de la edad para cardiopatía isquémica es de 1.4. La interpretación sería:

• Por cada año aumenta el Odds en 1.4.
• El riesgo de accidente cardiovascular aumenta al aumentar la edad. Interpretación en palabras comunes.

Otras interpretaciones

“Interpretación: aquellas participantes con sobrepeso-obesidad en la infancia (principalmente las siluetas 5 a 8-9) presentaron un incremento en el riesgo de sufrir depresión en la edad adulta comparadas con aquellas con peso normal en su niñez (silueta 3). Obsérvense las OR asociadas a dichas dummy: 1,29; 1,39; 1,98 y 2,43”¹

1. Fragmento de Bioestadística amigable (Spanish Edition) Miguel Ángel Martínez González.

Prueba de hipótesis en la regresión logística

• Se basa en la prueba de Wald que utiliza en estadístico Z y la distribución normal para probar la hipótesis nula de que un coeficiente en particular es 0.
• Esta prueba se basa en la relación entre el estimador (como el coeficiente de un predictor en la regresión), su error estándar, y una distribución \(\chi^2\)
• El valor Z se calcula dividiendo el valor del coeficiente entre su error estándar y el resultado se compara con los valores de tabla.

Devianza

• Se refiere a una medida de bondad de ajuste (qué tan bien un modelo estadístico se ajusta a un conjunto de observaciones) de un modelo estadístico comparado con un modelo perfecto

• La devianza en la regresión logística se calcula como el doble de la diferencia entre el logaritmo de la verosimilitud del modelo saturado y el logaritmo de la verosimilitud del modelo de regresión logística en cuestión

• Verosimilitud: probabilidad de observar los datos dados los parámetros del modelo

Devianza

Interpretación

• Siempre debe interpretarse en el contexto
• Una devianza más baja indica que el modelo en cuestión tiene un mejor ajuste a los datos. Sin embargo, una devianza muy baja podría sugerir un sobreajuste
• La devianza se utiliza para comparar modelos: un modelo con una devianza más baja se considera que tiene un mejor ajuste a los datos

Devianza residual

Se refiere a la devianza calculada utilizando las predicciones del modelo, y se usa para evaluar qué tan bien el modelo se ajusta a los datos observados

Devianza residual

Call:
glm(formula = low ~ smoke, family = binomial(), data = birthwt)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.0871     0.2147  -5.062 4.14e-07 ***
smoke         0.7041     0.3196   2.203   0.0276 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 234.67  on 188  degrees of freedom
Residual deviance: 229.80  on 187  degrees of freedom
AIC: 233.8

Number of Fisher Scoring iterations: 4

Supuestos del modelo

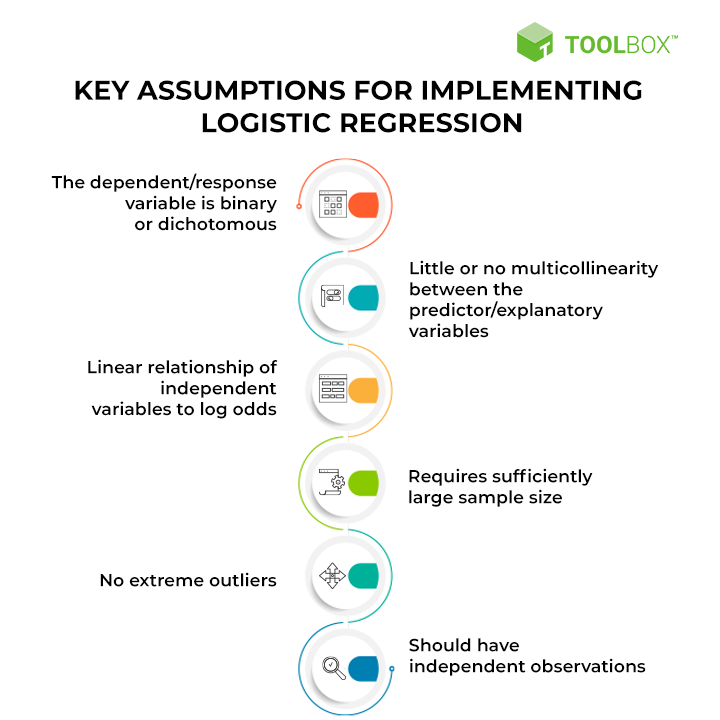
Supuestos del modelo

1. Relación entre variables independientes y el logit de la variable dependiente
2. Independencia de observaciones
3. Ausencia de multicolinealidad
4. Categorías mutuamente excluyentes y exhaustivas en la variable dependiente
5. Ausencia de valores atípicos
6. Muestra lo suficientemente grande: e recomienda un mínimo de 10 eventos por cada predictor en el modelo
7. Linealidad en los log-odds para variables continuas

Prueba de Hosmer-Lemeshow

Prueba de Hosmer-Lemeshow

• La prueba de Hosmer-Lemeshow es una prueba estadística que se utiliza para evaluar la bondad de ajuste de un modelo de regresión logística.

• Esta prueba compara las frecuencias observadas con las frecuencias esperadas de los eventos en grupos de riesgo, para determinar si el modelo predice correctamente la probabilidad del evento en diferentes niveles de probabilidad.

• La prueba se basa en dividir las observaciones en deciles o grupos según sus probabilidades predichas por el modelo y luego comparar el número de eventos observados y esperados en cada grupo.

• La hipótesis nula ((H_0)) de la prueba es que no hay una diferencia significativa entre las frecuencias esperadas y observadas, lo cual sugiere que el modelo tiene un buen ajuste.

Interpretación:

• Si el p-valor de la prueba de Hosmer-Lemeshow es mayor que 0.05, se acepta la hipótesis nula ((H_0)), lo que indica que no hay diferencias significativas entre las frecuencias observadas y esperadas, y se considera que el modelo se ajusta bien a los datos.
• Si el p-valor es menor que 0.05, se rechaza la hipótesis nula, lo que sugiere que el modelo no se ajusta bien a los datos.

Prueba de Hosmer-Lemeshow

Precisión del modelo

• Sensibilidad
• Especificidad
• Curvas ROC

Pseudo \(R^2\)

• Interpretación similar a la de una regresión lineal
• Hay varías maneras de estimarlo:
  • McFadden
  • Nagelkerke
  • Cox y Snell
  • Efron

Psuedo \(R^2\)

$N
[1] 189

$R2
[1] 0.03575429

Estrategías en el análisis multivariado

Algunas estrategias del análisis multivariado

Las siguientes estrategias fueron tomadas del libro de Bioestadística de Celis

• Identificación de las variables que se incluirán. Para definir la lista de variables candidatas, se deberán considerar todas aquellas que tengan un nivel de significancia menor de 0.25. A estas variables también se deberán agregar aquellas que tengan alguna importancia en relación con la variable dependiente o con las variables independientes más importantes.

Algunas estrategias del análisis multivariado

• Después de definir la lista de variables candidatas para el modelo multivariado, se identificarán las variables que tengan una importancia estadísticamente significativa en el modelo. Para hacerlo, el modelo se podrá construir agregando variables a partir de aquella que muestra la mayor asociación.
• Alternativamente se podrá integrar un modelo con todas las variables candidatas y, poco a poco, retirar aquellas que muestren la menor asociación. La agregación o eliminación de variables a partir del modelo inicial podrá hacerse individualmente o en grupo.

Algunas estrategias del análisis multivariado

• Para seleccionar las variables con las que se definirá el modelo, se deberán tomar en cuenta, al menos, dos aspectos: la significancia estadística y la probable confusión que introduzcan en las asociaciones de interés
• Es necesario tomar en cuenta que no es indispensable incluir en el modelo todas las variables que sean estadísticamente significativas

Algunas estrategias del análisis multivariado

• Una vez obtenido el modelo que incluya las variables esenciales, deberemos prestar atención a las variables cuantitativas, sobre todo a su linealidad, en los términos descritos en la sección de “Variables cualitativas y cuantitativas”.
• Al igual que para el caso de la regresión múltiple, un aspecto importante en relación con las covariables es la colinealidad.

Algunas estrategias del análisis multivariado

• Luego es necesario explorar la interacción que pudiera existir entre variables.
• Después identificamos las variables confusoras.
• Concluimos evaluando la bondad de ajuste del modelo

Algunas estrategias del análisis multivariado

p < 0.05 La variable Xi es, al menos, una variable predictora, se comporte o no como variable de confusión Debe permanecer en el modelo

p > 0.25 Variable no relevante Debe eliminarse del modelo

p > 0,05 y < 0,25 Debe observarse el cambio que se produce en la OR de la variable principal de análisis tras la inclusión/exclusión de la hipotética variable de confusión Si el cambio es grande (10-15%), la variable produce distorsión y debe permanecer en el modelo; es un factor de confusión