plot(LungCap, Height, main = "LungCap vs Height") #Utilice attach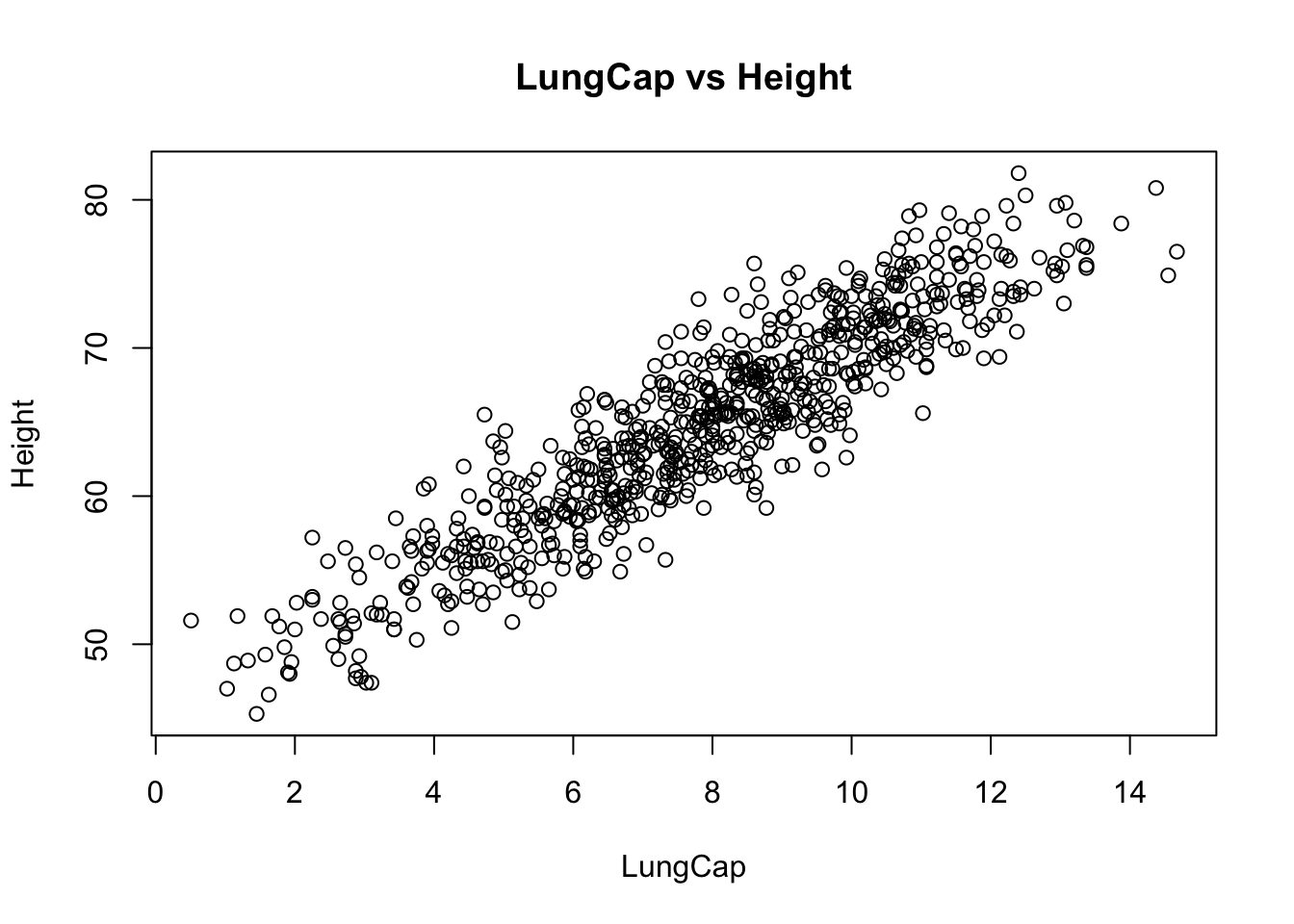
plot(LungCap, Age, main= "LungCap vs Age" )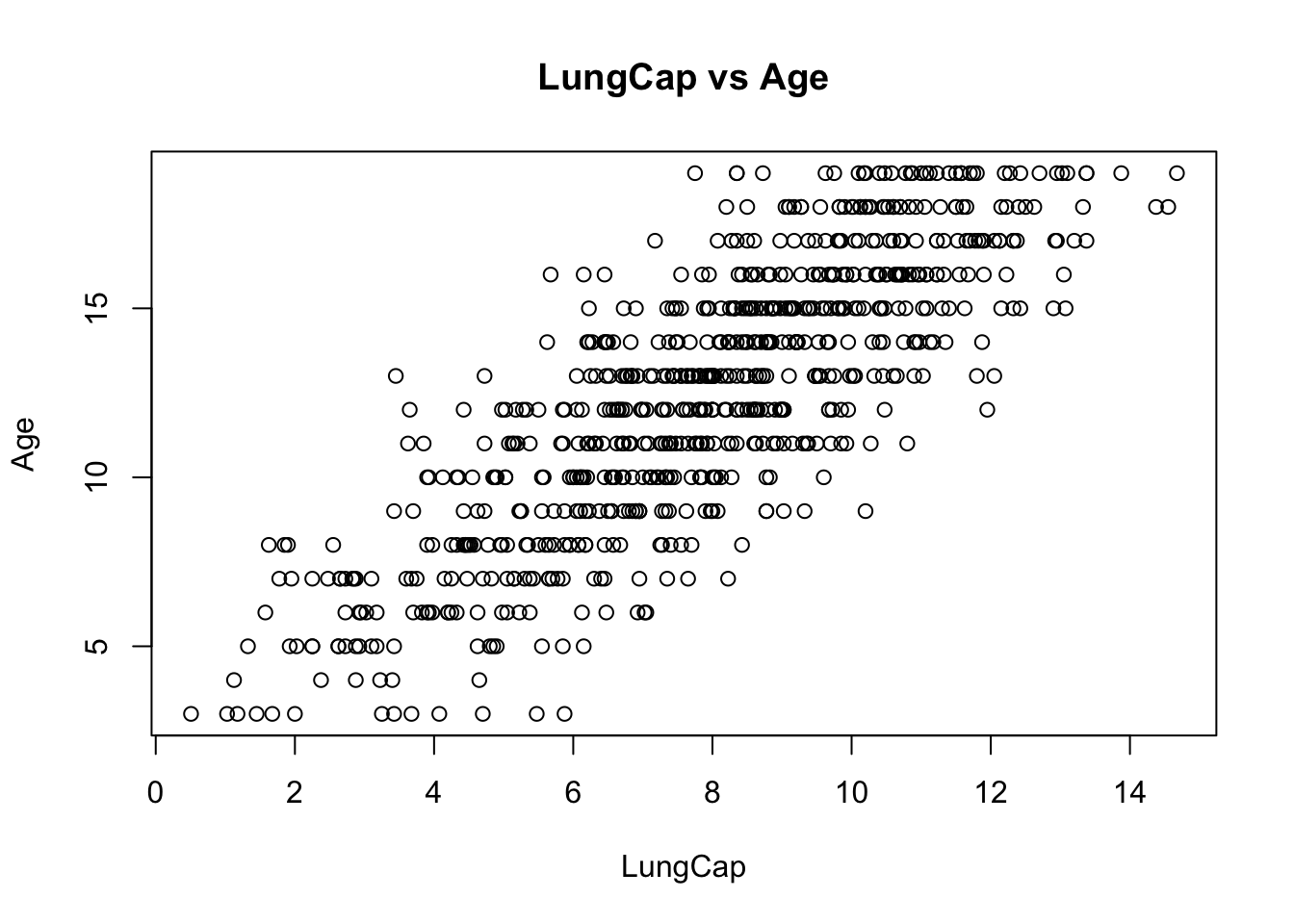
Para el siguiente ejemplo utilice la base de datos “LungCapData”.
Las capacidades pulmonares se refieren a los distintos volúmenes de aire característicos en la respiración humana. Un pulmón humano puede almacenar alrededor de 6 litros de aire en su interior, pero una cantidad significativamente menor es la que se inhala y exhala durante la respiración.
La base de datos LungCapData contiene datos de una serie de pacientes sobre la capacidad de fumadores y no fumadores por edad, sexo y altura. Esta base de datos es pública del autor Mike Marin, quien provee una serie de tutoriales sobre estadística y R de forma gratuita; tutoriales que recomendamos ampliamente. La base de datos consta de las siguientes variables:
Un grupo de investigadores desea conocer como influye la edad (Age) y la estatura (Hieght) sobre la capacidad pulmonar, para ello se plantea realizar una regresión lineal múltiple.
Después de importar la base de datos di un attach.


Para añadir variables al modelo solo se deben separar por un signo de suma:
Call:
lm(formula = LungCap ~ Age + Height, data = LungCapData)
Residuals:
Min 1Q Median 3Q Max
-3.4080 -0.7097 -0.0078 0.7167 3.1679
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -11.747065 0.476899 -24.632 < 2e-16 ***
Age 0.126368 0.017851 7.079 3.45e-12 ***
Height 0.278432 0.009926 28.051 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.056 on 722 degrees of freedom
Multiple R-squared: 0.843, Adjusted R-squared: 0.8425
F-statistic: 1938 on 2 and 722 DF, p-value: < 2.2e-16Los gráficos indican que se cumplen los supuestos establecidos para los residuales
Pearson's product-moment correlation
data: Age and Height
t = 40.923, df = 723, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8123578 0.8564338
sample estimates:
cor
0.8357368 Aunque el coeficiente de correlación nos dice que se presenta una alta correlación entre las dos variables independientes. El VIF indica que la colinealidad no es importante para el modelo. La proporción de variabilidad de la variables edad no es explicada por el resto de las variables predictoras del modelo Height
También podemos emplear este código:
La capacidad pulmonar se afecta por fumar, sin embargo se afecta también por la edad y por la talla del individuo. Ahora, los investigadores se preguntan si se puede construir un modelo con estas tres variables. Además desean probar si fumar permanece asociado a la capacidad pulmonar después de ajustar por edad y talla.
Gráfico para ver la relación que tiene el fumar con la capacidad pulmonar
Resultados del modelo
Call:
lm(formula = LungCap ~ Age + Height + Smoke)
Residuals:
Min 1Q Median 3Q Max
-3.4840 -0.7135 0.0358 0.7088 3.0392
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -11.808195 0.469120 -25.171 < 2e-16 ***
Age 0.136916 0.017677 7.745 3.24e-14 ***
Height 0.278432 0.009761 28.525 < 2e-16 ***
Smokeyes -0.648583 0.128099 -5.063 5.24e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.039 on 721 degrees of freedom
Multiple R-squared: 0.8484, Adjusted R-squared: 0.8477
F-statistic: 1345 on 3 and 721 DF, p-value: < 2.2e-16Supuestos
Colinealidad
Utilizando performance
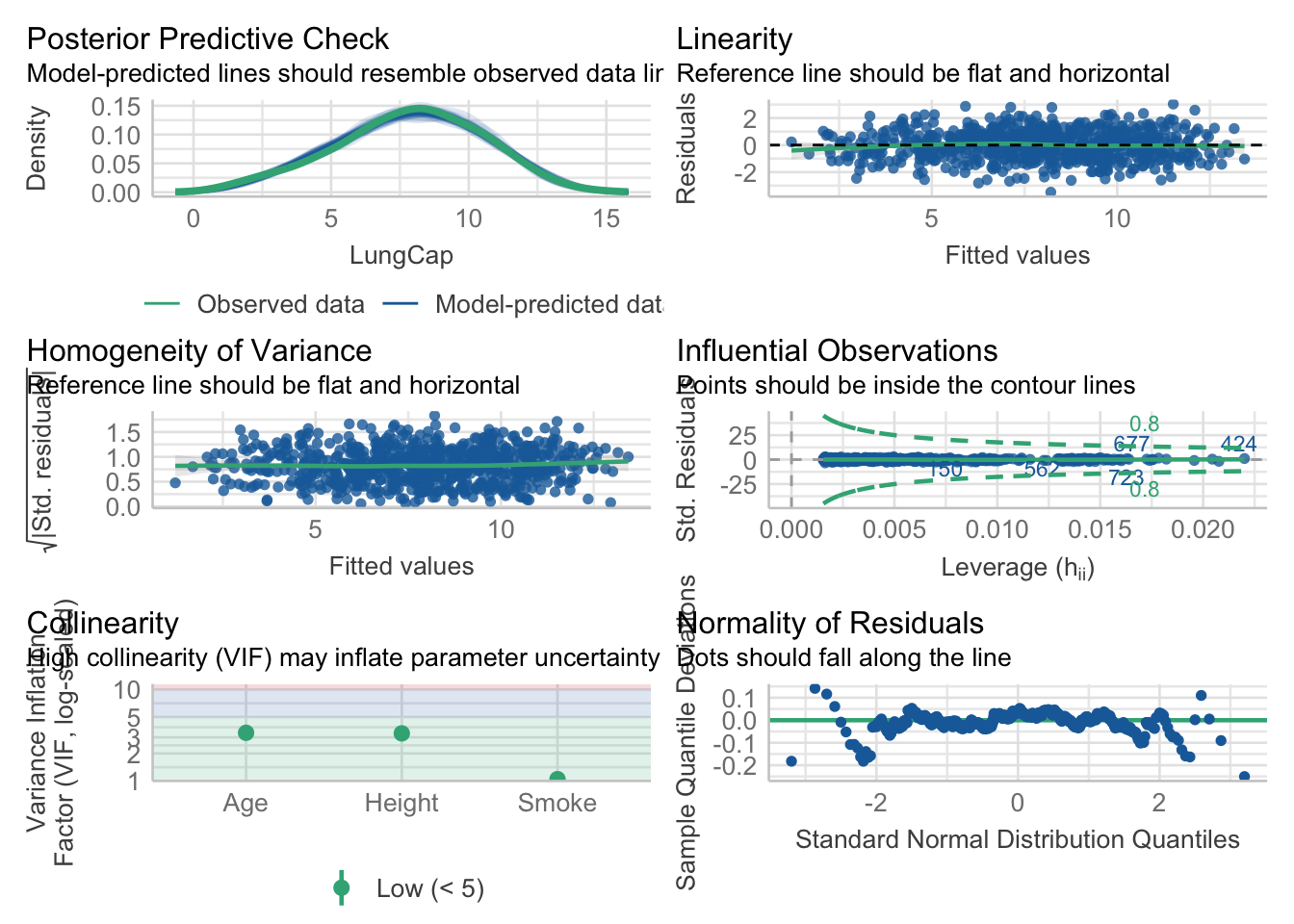
# Check for Multicollinearity
Low Correlation
Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
Age 3.36 [2.98, 3.81] 1.83 0.30 [0.26, 0.34]
Height 3.32 [2.94, 3.76] 1.82 0.30 [0.27, 0.34]
Smoke 1.05 [1.01, 1.25] 1.02 0.96 [0.80, 0.99]Interprete su modelo
¿Influirán en el modelo el haber nacido por cesárea y el género de los individuos?
Gráfico para ver la relación que tiene el fumar con la capacidad pulmonar
LungCapData|>
ggplot(mapping = aes(x=Caesarean, y=LungCap, fill = Caesarean))+
geom_boxplot(col= "black", alpha = 0.5)+
scale_fill_manual(values = c("cyan4", "cyan3"))+
theme_linedraw()+labs(x="Cesárea", y= "Capacidad pulmonar")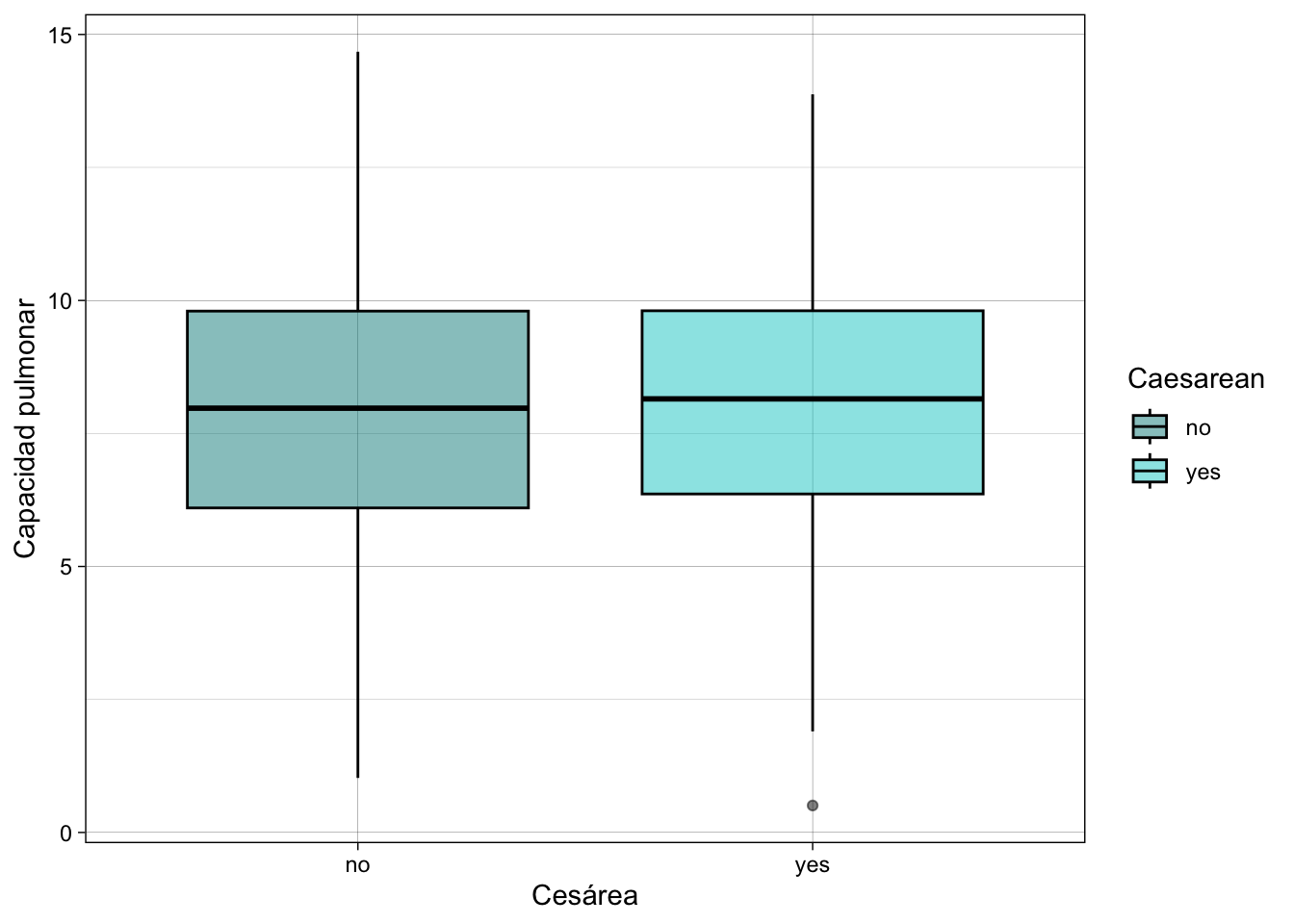
LungCapData|>
ggplot(mapping = aes(x=Gender, y=LungCap, fill = Gender))+
geom_boxplot(col= "black", alpha = 0.5)+
scale_fill_manual(values = c("cyan4", "cyan3"))+
theme_linedraw()+labs(x="Género", y= "Capacidad pulmonar")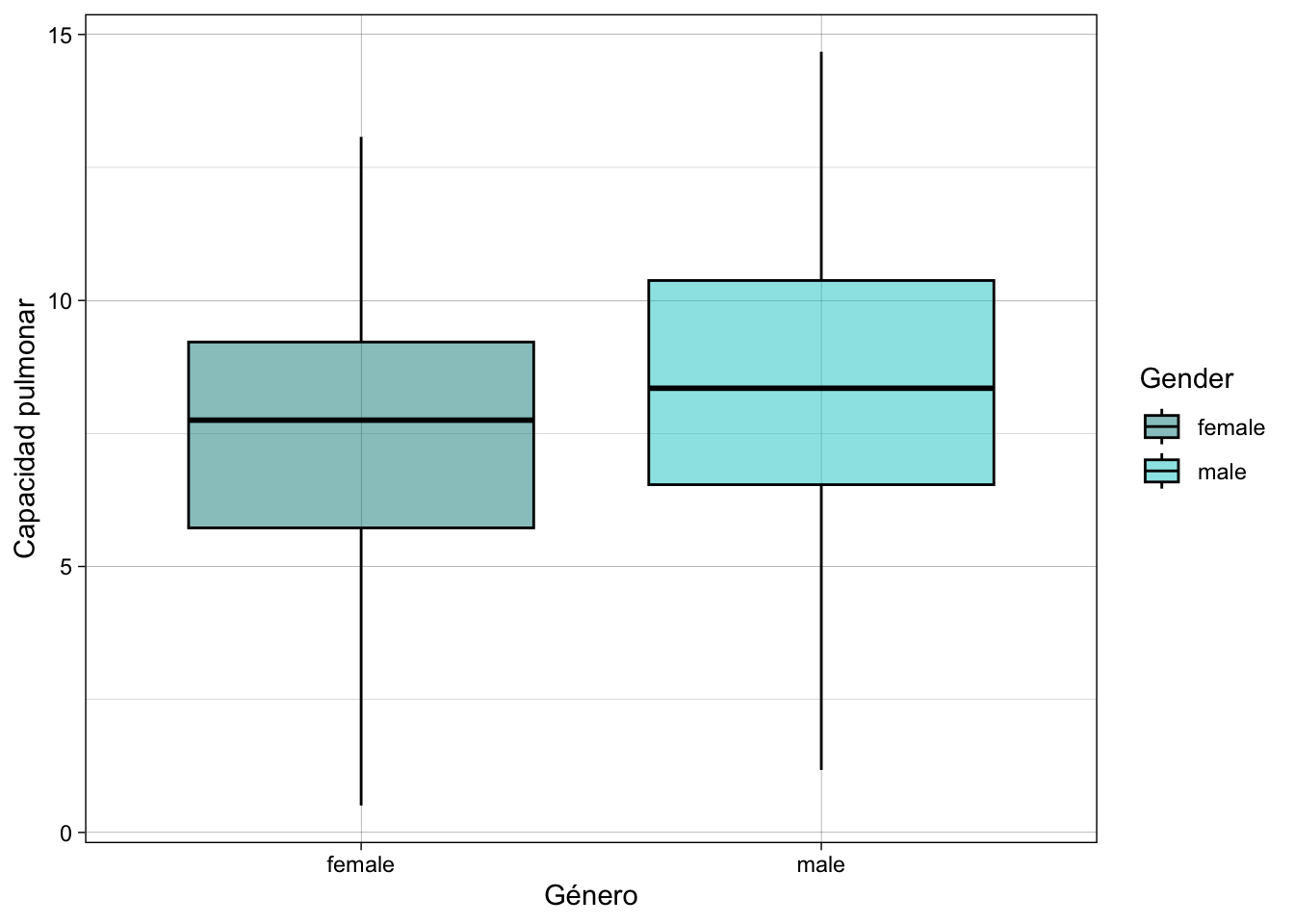
Construcción del modelo
Resultados del modelo
Call:
lm(formula = LungCap ~ Age + Height + Smoke + Caesarean + Gender)
Residuals:
Min 1Q Median 3Q Max
-3.3388 -0.7200 0.0444 0.7093 3.0172
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -11.32249 0.47097 -24.041 < 2e-16 ***
Age 0.16053 0.01801 8.915 < 2e-16 ***
Height 0.26411 0.01006 26.248 < 2e-16 ***
Smokeyes -0.60956 0.12598 -4.839 1.60e-06 ***
Caesareanyes -0.21422 0.09074 -2.361 0.0185 *
Gendermale 0.38701 0.07966 4.858 1.45e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.02 on 719 degrees of freedom
Multiple R-squared: 0.8542, Adjusted R-squared: 0.8532
F-statistic: 842.8 on 5 and 719 DF, p-value: < 2.2e-16Supuestos
Colinealidad
Utilizando performance
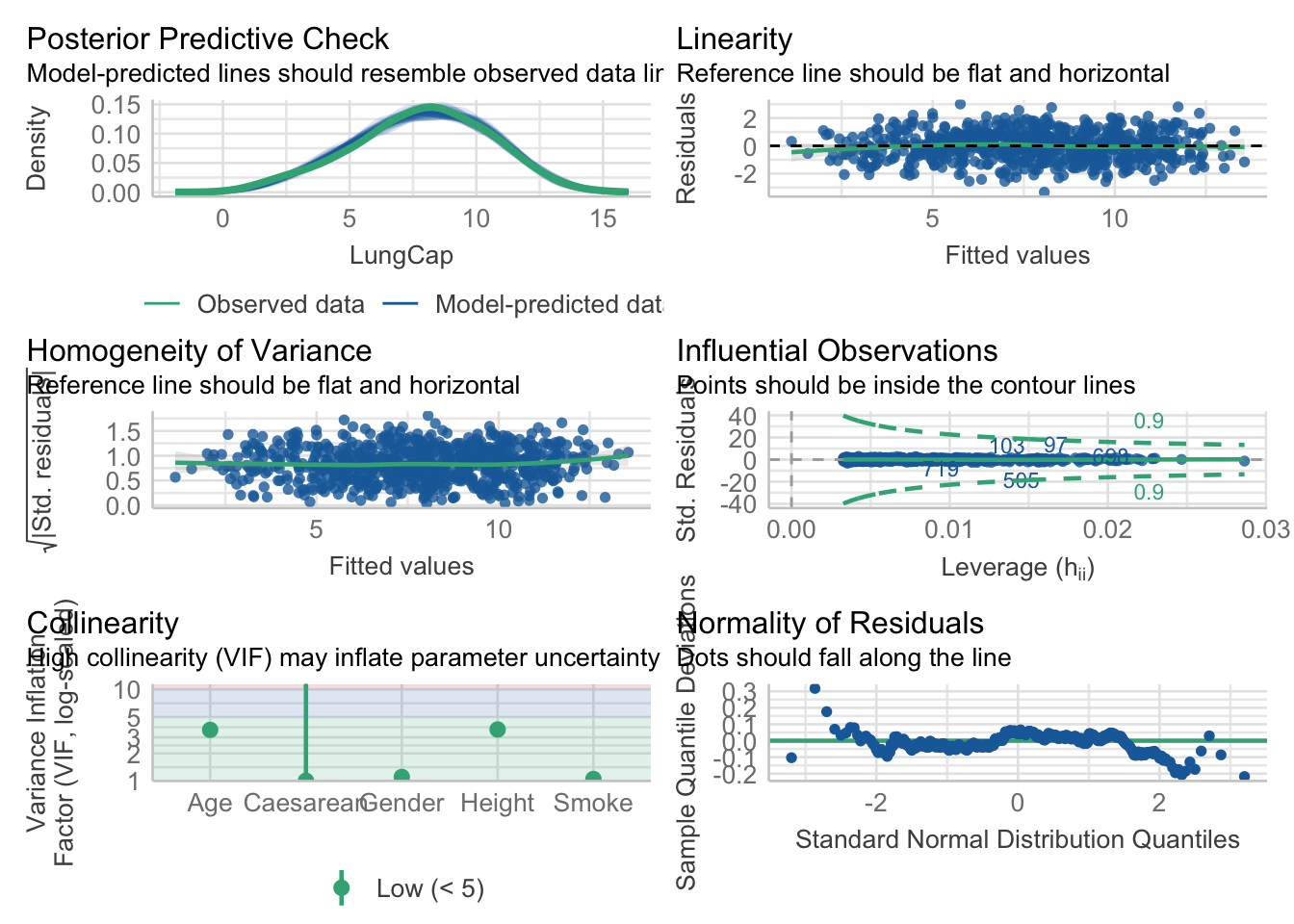
# Check for Multicollinearity
Low Correlation
Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
Age 3.62 [3.21, 4.11] 1.90 0.28 [0.24, 0.31]
Height 3.66 [3.24, 4.15] 1.91 0.27 [0.24, 0.31]
Smoke 1.05 [1.01, 1.24] 1.02 0.95 [0.80, 0.99]
Caesarean 1.00 [1.00, 33111.14] 1.00 1.00 [0.00, 1.00]
Gender 1.11 [1.05, 1.24] 1.05 0.90 [0.81, 0.96]Utilice la base de datos (“bodyfat.txt”) y construya un modelo que permita predecir la circunferencia de cintura de un paciente (Abdomen) dadas el resto de medidas antropométicas.
Puede construir un modelo añadiendo todas la variables e ir descartando aquellas que no aporten al modelo (sin significancia) o puede ir añadiendo variables hasta construir un modelo adecuado. Un modelo valido es aquel en el que todas la variables aportan a la variable de respuesta (son significativas). De hecho la prueba de hipótesis que deseamos probar es que adición de un variable al modelo aumente la predicción del mismo.
bodyfat <- read.csv("Bases/bodyfat.txt", sep="", stringsAsFactors=TRUE)# Código para importa base de datos
attach(bodyfat)# Adjuntar para facilitar el análisisThe following objects are masked from LungCapData:
Age, Heightmod1 <- lm(Abdomen~Fat+Age+Weight+Height+Neck+Chest+Hip+Thigh+
Knee+Ankle+Biceps+Forearm+Wrist)
summary(mod1)
Call:
lm(formula = Abdomen ~ Fat + Age + Weight + Height + Neck + Chest +
Hip + Thigh + Knee + Ankle + Biceps + Forearm + Wrist)
Residuals:
Min 1Q Median 3Q Max
-6.8759 -1.8283 0.0655 1.9419 6.8826
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.26083 10.59376 0.591 0.555086
Fat 0.35490 0.03213 11.044 < 2e-16 ***
Age 0.08945 0.01901 4.706 4.29e-06 ***
Weight 0.11421 0.03197 3.572 0.000429 ***
Height -0.05587 0.05849 -0.955 0.340439
Neck 0.21360 0.14227 1.501 0.134588
Chest 0.36403 0.05566 6.540 3.72e-10 ***
Hip 0.34937 0.08642 4.043 7.14e-05 ***
Thigh 0.06737 0.08840 0.762 0.446770
Knee -0.13250 0.14728 -0.900 0.369233
Ankle -0.21848 0.13446 -1.625 0.105498
Biceps -0.21958 0.10361 -2.119 0.035093 *
Forearm -0.24108 0.12171 -1.981 0.048774 *
Wrist -0.03283 0.33237 -0.099 0.921409
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.625 on 238 degrees of freedom
Multiple R-squared: 0.9438, Adjusted R-squared: 0.9407
F-statistic: 307.5 on 13 and 238 DF, p-value: < 2.2e-16Mediante prueba y error agregue y quite variables hasta obtener un modelo ideal. Tome en cuenta los valores de \(p\) y los valores de \(R^2\)
Call:
lm(formula = Abdomen ~ Fat + Age + Weight + Chest + Hip + Forearm)
Residuals:
Min 1Q Median 3Q Max
-8.2318 -2.0735 0.0011 1.9413 6.9347
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.09712 6.45186 -0.635 0.526002
Fat 0.36252 0.03015 12.025 < 2e-16 ***
Age 0.08940 0.01544 5.791 2.14e-08 ***
Weight 0.08410 0.02281 3.688 0.000279 ***
Chest 0.39939 0.05244 7.616 5.67e-13 ***
Hip 0.39078 0.07360 5.309 2.47e-07 ***
Forearm -0.30207 0.10993 -2.748 0.006444 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.654 on 245 degrees of freedom
Multiple R-squared: 0.9409, Adjusted R-squared: 0.9394
F-statistic: 649.9 on 6 and 245 DF, p-value: < 2.2e-16Los gráficos de residuales son:
Gráfica para ver la correlación entre la variables predictoras
corrplot 0.92 loaded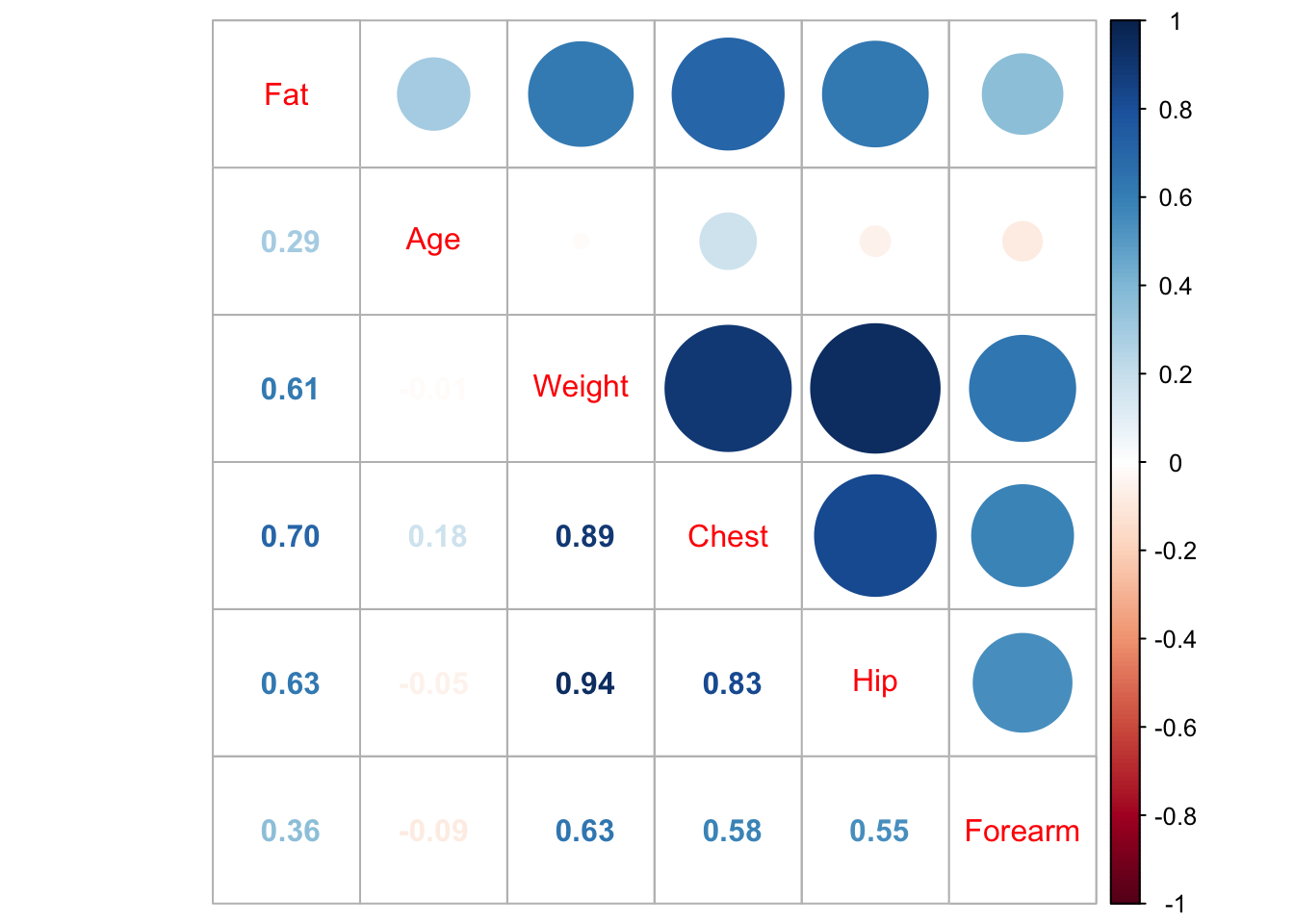
Se puede evaluar la colinealidad mediante el factor de inflación de varianza (VIF), utilizando la función vif del paquete car.
Loading required package: carData Fat Age Weight Chest Hip Forearm
2.268709 1.349220 16.010798 6.965926 9.909411 1.758610 Valores entre 5 y 10 indican posible presencia de colinealidad. Mayores a 10 indican alta colinealidad
Utilizando la base de datos sal_tension_arterial.csv cree un modelo de regresión lineal múltiple que permita predecir la tensión arterial sistólica (TAS) a partir de las variables predictoras de la base. Interprete su modelo y verifique los supuestos del mismo.