# Generar datos simulados para un conjunto pequeño
set.seed(123)
n_cases <- 15
n_controls <- 15
cases <- rnorm(n_cases, mean = 5, sd = 1) # Concentración más alta en casos
controls <- rnorm(n_controls, mean = 3, sd = 1) # Concentración más baja en controles
# Crear el vector de etiquetas (1 = caso, 0 = control)
outcome <- c(rep(1, n_cases), rep(0, n_controls))
biomarker_values <- c(cases, controls)
Datos <- data.frame(outcome, biomarker_values)Curvas ROC, AUC Y regresión logística
Aspectos teóricos
Edsaúl E. Pérez-Guerrero, PhD; edsaul.perezg@academicos.udg.mx
2024-11-20
Curvas ROC
La curva ROC (Receiver Operating Characteristic) es una representación gráfica de la sensibilidad (eje Y) frente a la especificidad (eje X) para un sistema clasificador binario a diferentes puntos de corte.
La curva ROC es una herramienta útil para seleccionar modelos y clasificadores basados en su rendimiento.
En ciencias de la salud, la curva ROC se utiliza para evaluar el rendimiento de un biomarcador, de una prueba de laboratorio o de un modelo de predicción.
Conceptos básicos
Sensibilidad
- La sensibilidad es la probabilidad de que un individuo con la enfermedad tenga un resultado positivo en la prueba diagnóstica.
Espesificidad
- La especificidad es la probabilidad de que un individuo sin la enfermedad tenga un resultado negativo en la prueba diagnóstica.
Punto de corte
- El punto de corte es el valor de la variable de interés que se utiliza para clasificar a los individuos en dos grupos.
Tablas 2X2 de clasificación
| Condición Predicha | |||
|---|---|---|---|
| Condición Real | Prueba (+) | Prueba (−) | |
| Enfermedad (+) | a | b | |
| Enfermedad (−) | c | d |
Tablas 2X2 de clasificación
Las fórmulas matemáticas para el cálculo de estas medidas son:
Sensibilidad=VPVP+FN
Especificidad=VNVN+FP
donde: VP = verdaderos positivos; FN = falsos negativos; VN = verdaderos negativos y FP = falsos positivos.
Una Curva ROC perfecta
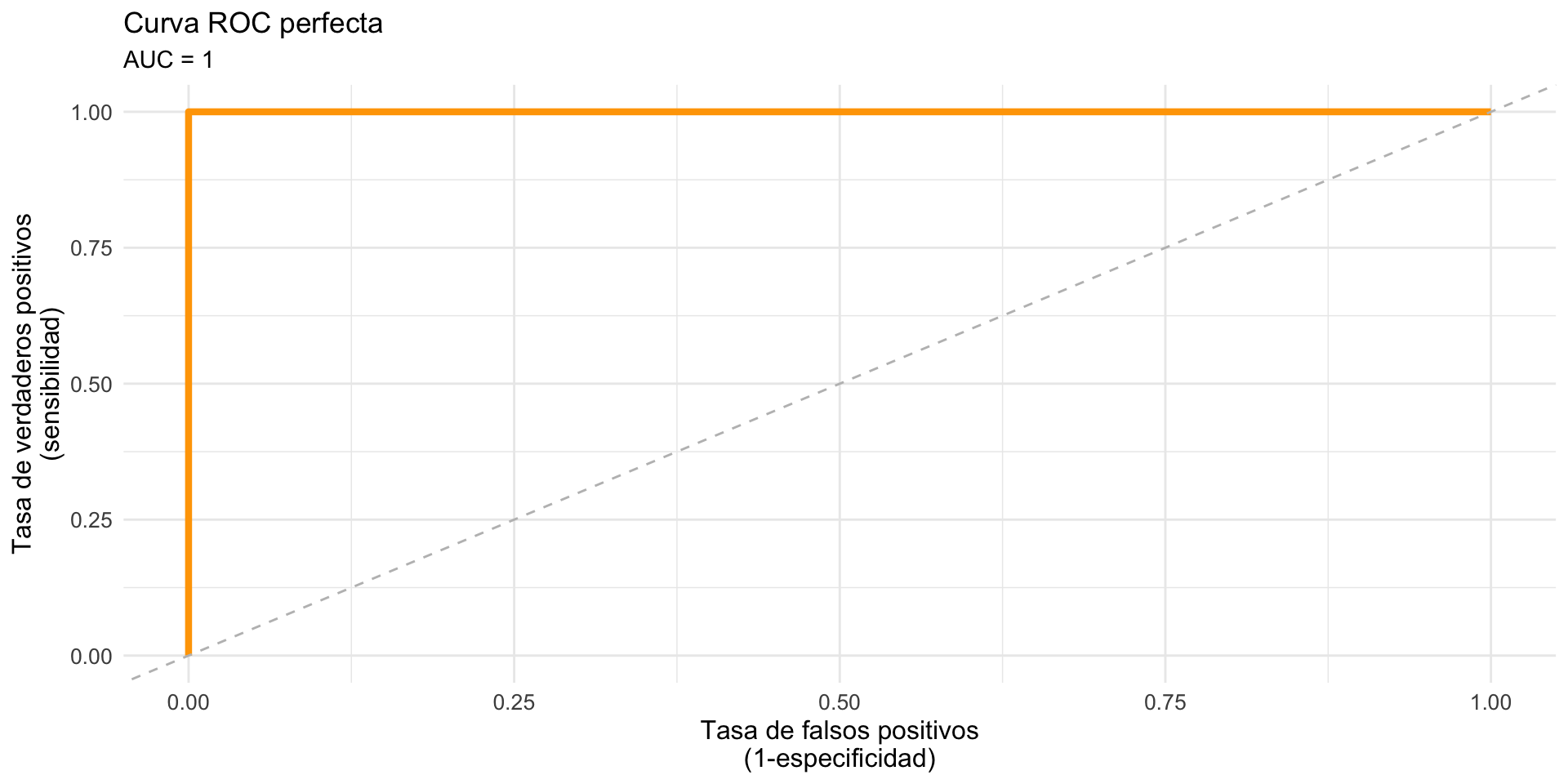
Figure 1
Una curva ROC no tan perfecta
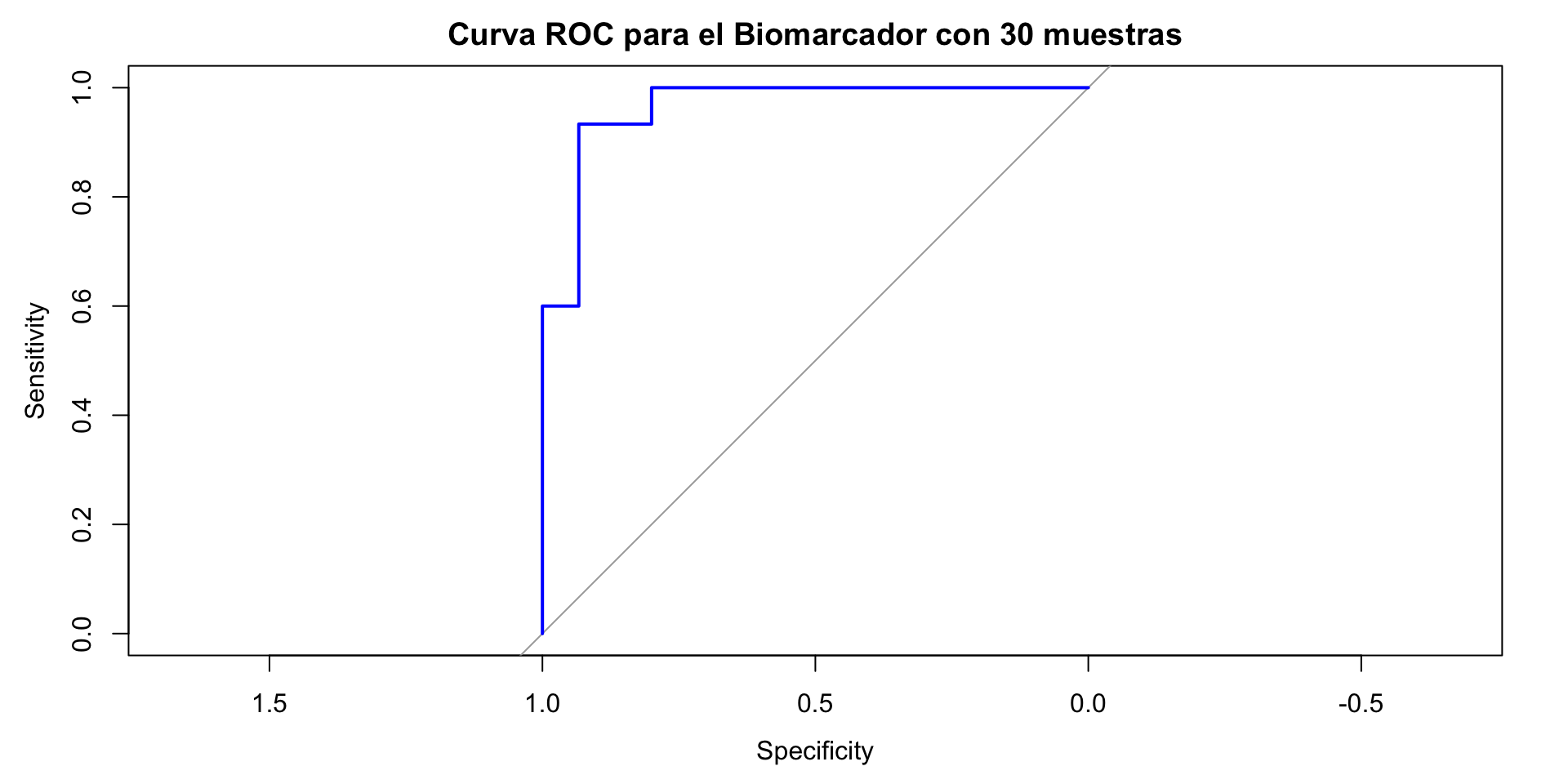
¿Cómo se grafica una curva ROC?
Vamos a generar una serie de datos para entender como es que se construye una curva ROC.
¿Cómo se grafica una curva ROC?
Vamos a ordenar y luego visualizar los datos
¿Cómo se grafica una curva ROC?
Realice un plot de los datos ordenados
¿Cómo se grafica una curva ROC?
Realice un plot de los datos ordenados
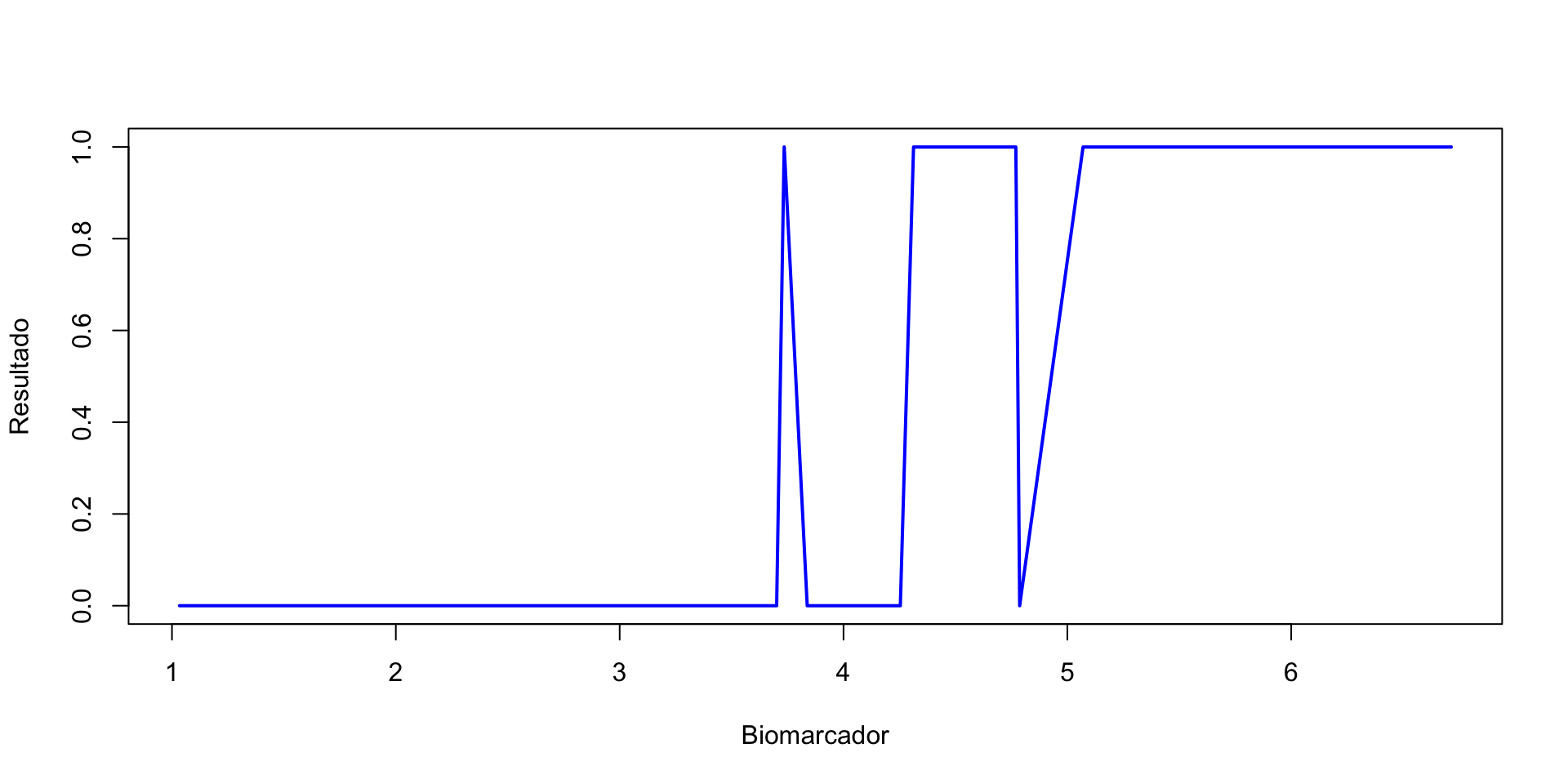
¿Qué es lo que nota?
¿Cómo se grafica una curva ROC?
- Ordena los datos del biomarcador (en este caso) de menor a mayor
- Definición de Puntos de Corte: Cada valor único de concentración se toma sucesivamente como un punto de corte (umbral). El algoritmo “recorre” los valores de concentración en orden y calcula sensibilidad y especificidad en cada punto de corte.
- El algoritmo calcula la sensibilidad y la especificidad para cada punto de corte.
- En cada punto de corte, se calcula la sensibilidad y la especificidad.Es decir, para umbral se identifica cuántos casos y controles se clasifican correctamente e incorrectamente.
¿Cómo se gráfica una curva ROC?
¿Cómo se gráfica una curva ROC?
¿Cómo se gráfica una curva ROC?
- ¿Por que la curva se desplaza a al derecha?
- Un desplazamiento hacia la derecha (disminución de especificidad) ocurre cuando un punto de corte incluye varios controles como falsos positivos (clasificándolos erróneamente como casos).
- La curva se desplaza hacia la derecha porque para detectar más verdaderos positivos (subir en el eje Y), inevitablemente tenemos que aceptar más falsos positivos (movernos a la derecha en el eje X). Es un compromiso inherente a cualquier clasificador binario
¿Cómo se gráfica una curva ROC?
Utilice el archivo de excel para realizar un cálculo manual de una curva ROC
¿Cómo se gráfica una curva ROC?
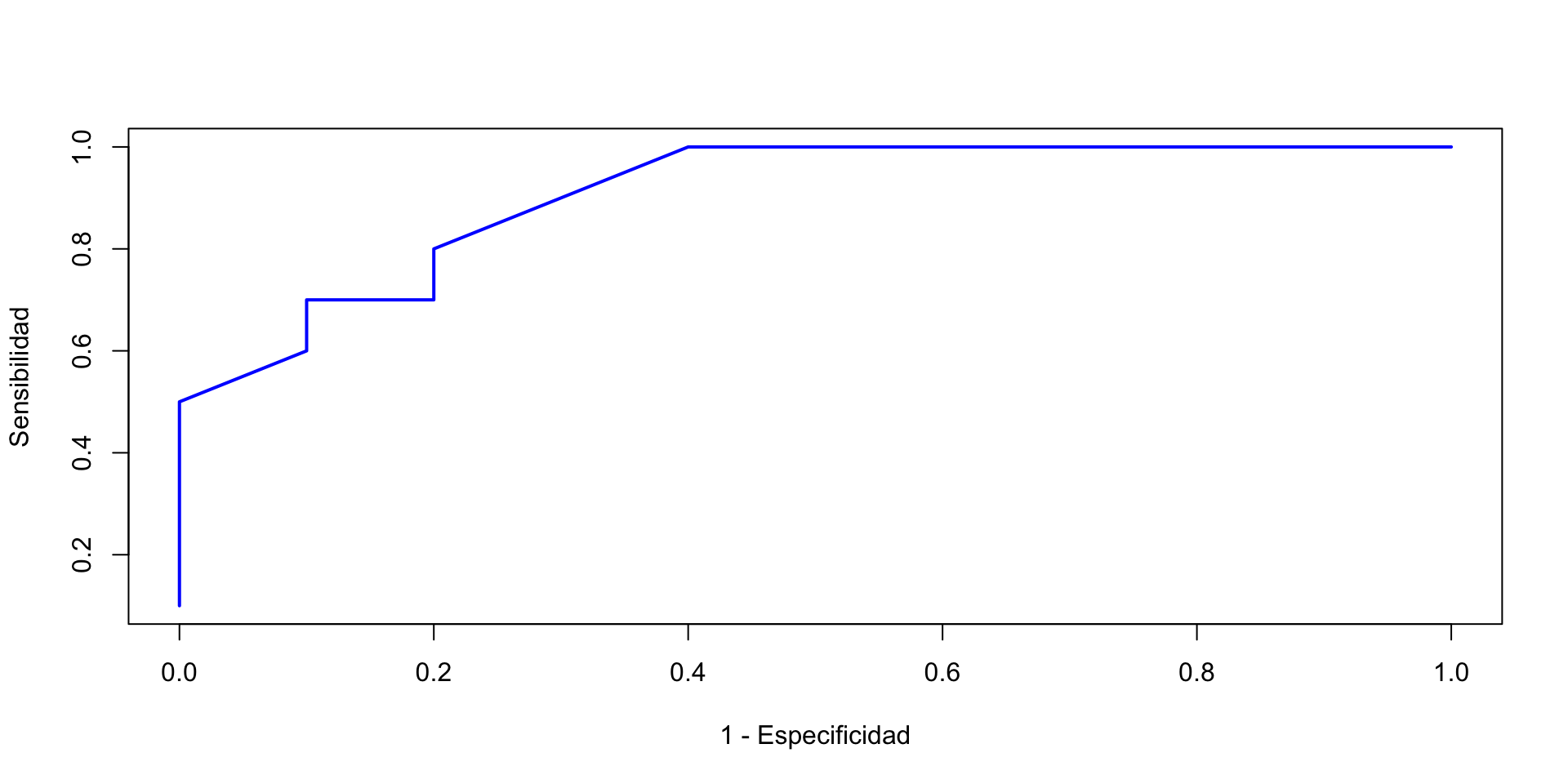
Área bajo la curva ROC (AUC)
- El área bajo la curva ROC (AUC) es una medida de la capacidad de un modelo para discriminar entre clases.
- Un modelo perfecto tendría un AUC de 1, mientras que un modelo aleatorio tendría un AUC de 0.5.
- Un AUC de 0.5 indica que el modelo no tiene capacidad de discriminación.
- Un AUC de 0.7 a 0.8 se considera aceptable, mientras que un AUC de 0.8 a 0.9 es excelente.
Curvas ROC y AUC en R
Curvas ROC y AUC en R
Curvas ROC y AUC en R
Ahora podemos graficar
Curvas ROC y AUC en R
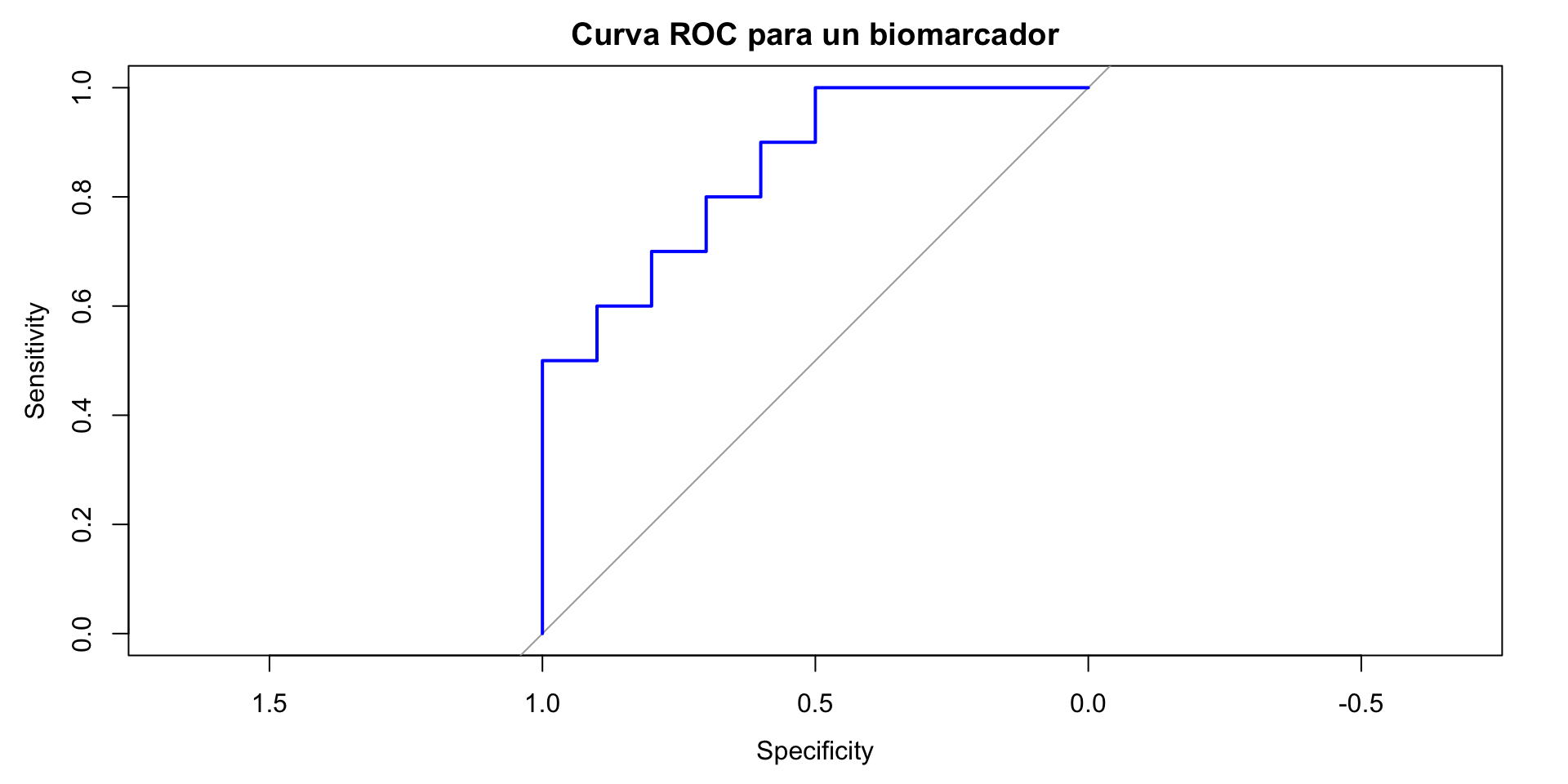
Curvas ROC y AUC en R
Podemos modificar la apariencia de la curva ROC
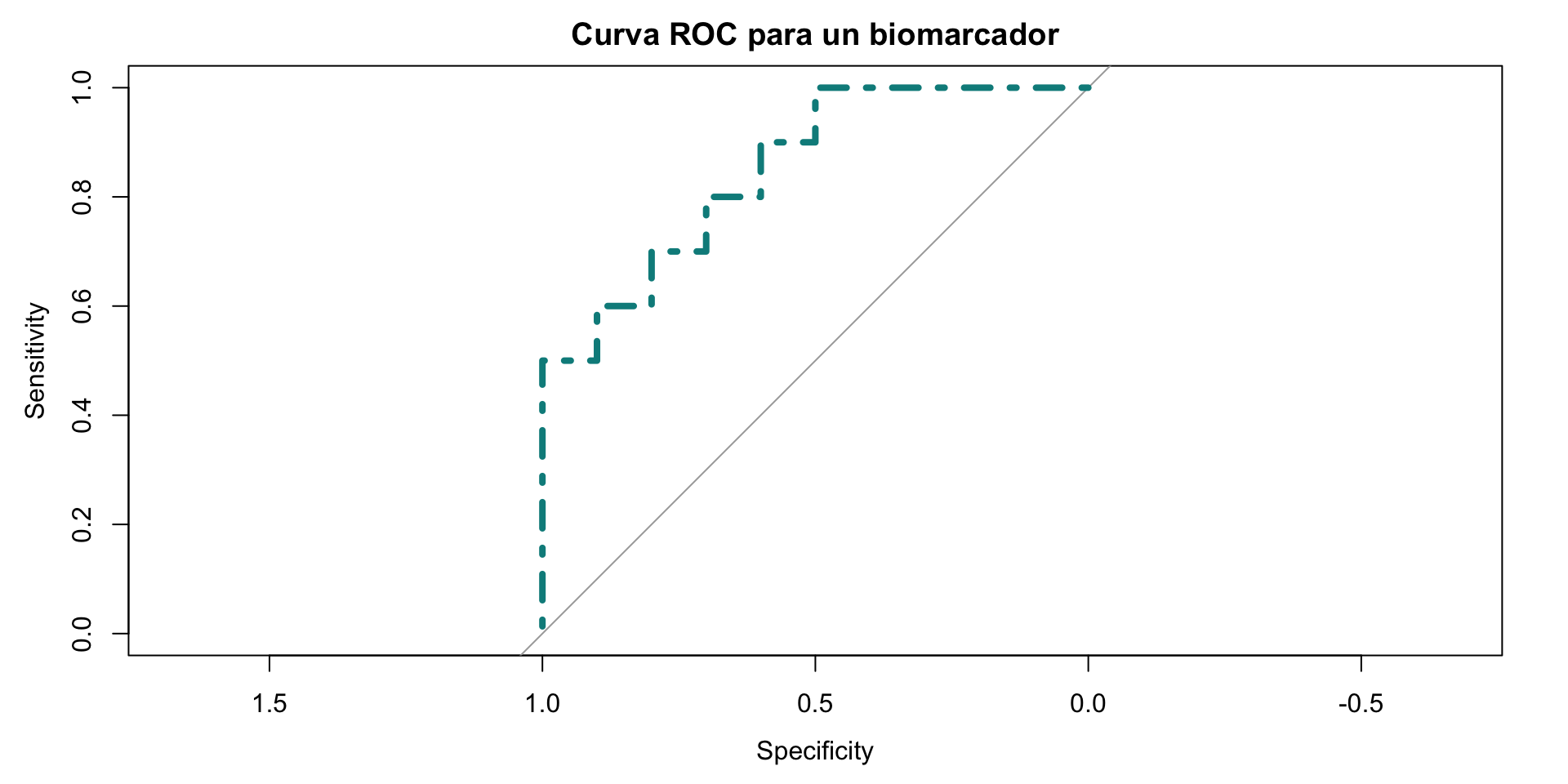
Curvas ROC y AUC en R
Otras opciones de gráficas
Curvas ROC y AUC en R
Otras opciones de gráficas
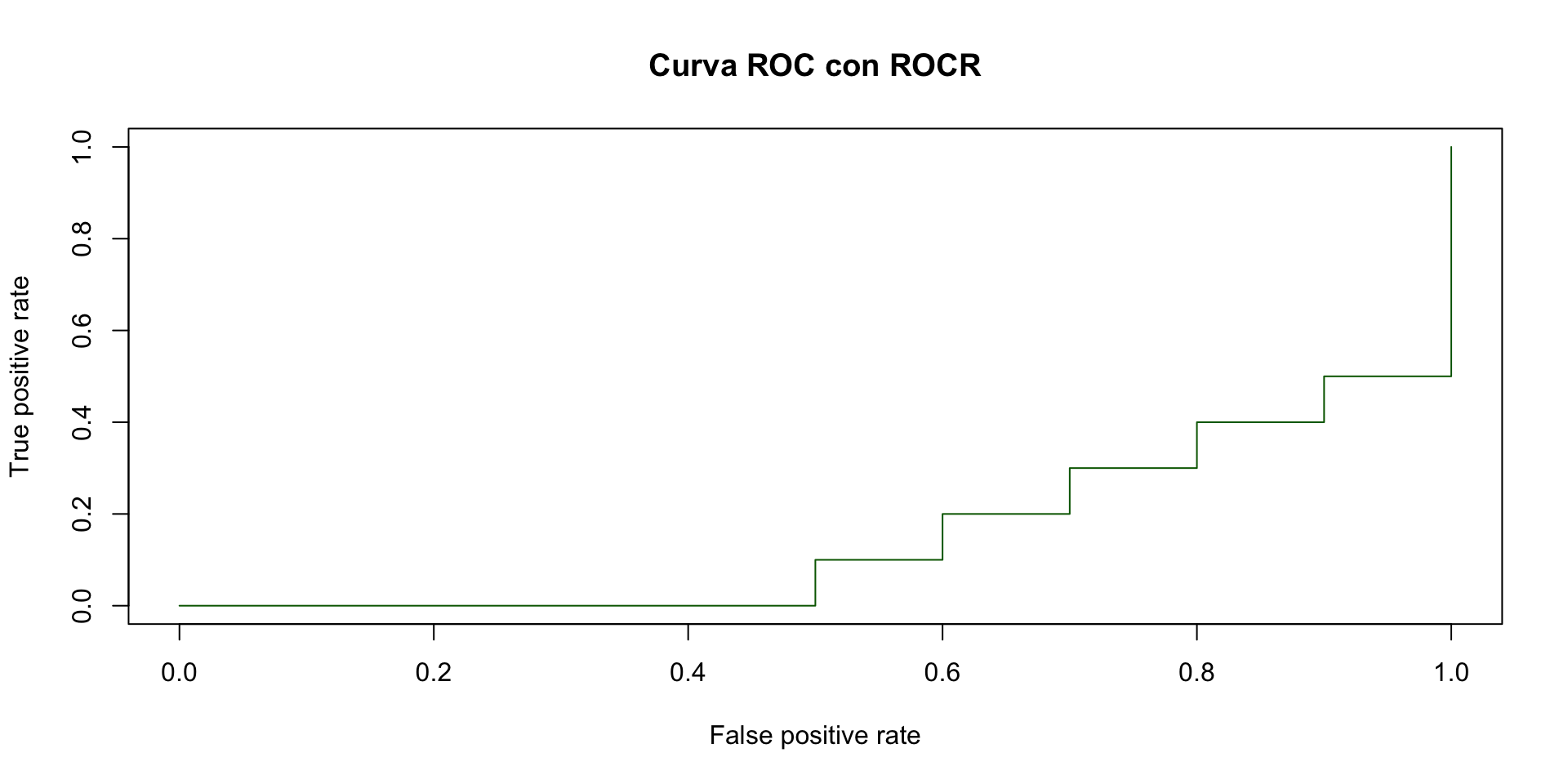
Curvas ROC y AUC en R
Otras opciones de gráficas
library(ggplot2)
# Convertir a un dataframe para ggplot2
roc_data <- data.frame(
specificity = rev(roc_curve$specificities),
sensitivity = rev(roc_curve$sensitivities)
)
# Graficar con ggplot2
ggplot(roc_data, aes(x = 1 - specificity, y = sensitivity)) +
geom_line(color = "blue") +
labs(title = "Curva ROC con ggplot2", x = "1 - Especificidad", y = "Sensibilidad") +
theme_minimal()Curvas ROC y AUC en R
Otras opciones de gráficas
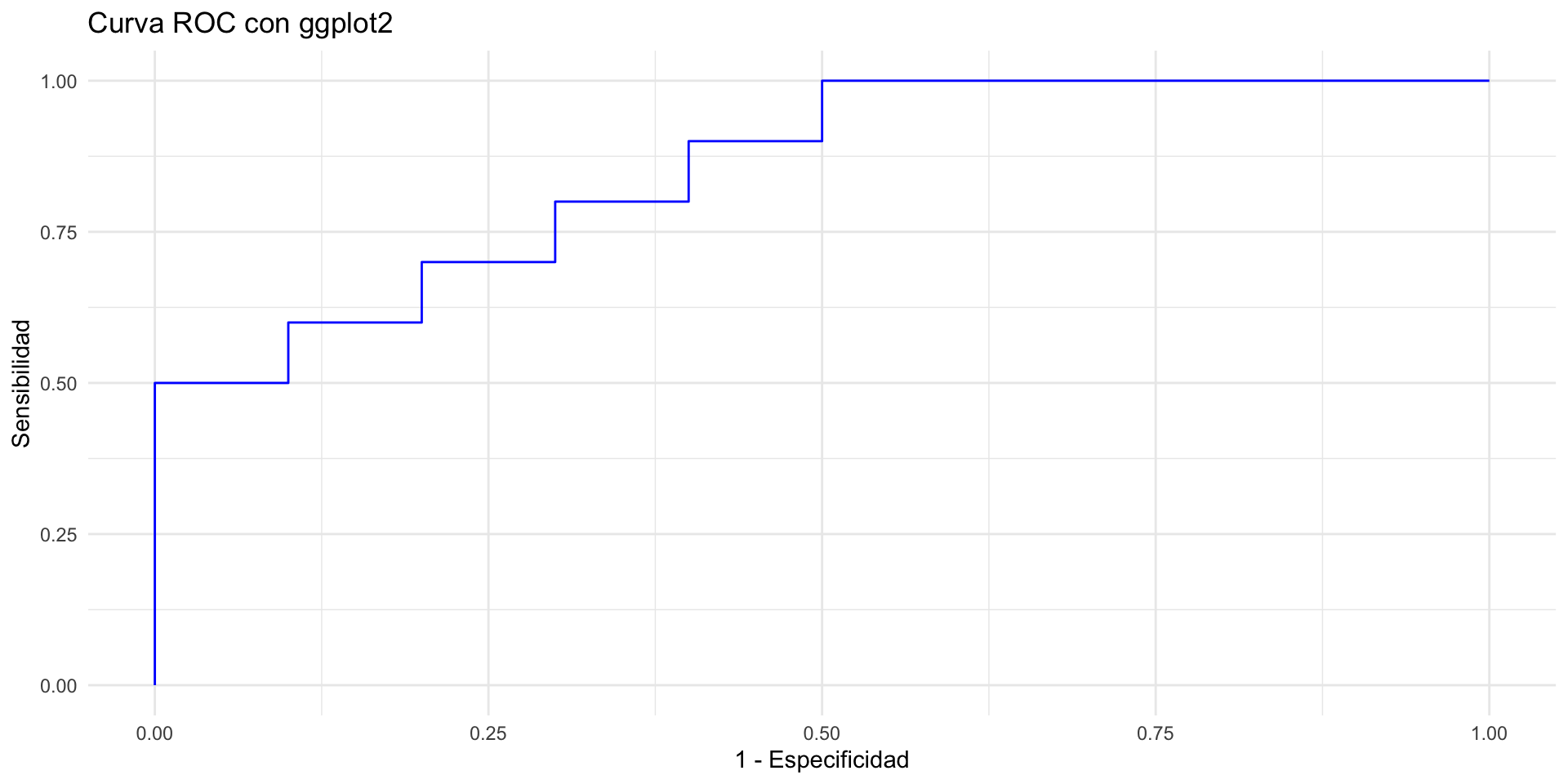
AUC en R
Selección de un punto de corte
# Extraer los valores de sensibilidad, especificidad y concentraciones
sensibilidad <- roc_curve$sensitivities[-1] # Remover el primer valor
especificidad <- roc_curve$specificities[-1] # Remover el primer valor
concentraciones <- rev(sort(df$Concentración)) # Ordenar las concentraciones de mayor a menor
# Crear un data.frame con los valores de concentración, sensibilidad y especificidad
roc_data <- data.frame(
Concentración = concentraciones,
Sensibilidad = sensibilidad,
Especificidad = especificidad
)
# Imprimir el data.frame
print(roc_data)Ejercicios curva ROC
La base de datos Base_ROC.csv contiene datos de 165 pacientes, que padecen cierta enfermedad. A todos, se les tomaron muestras de sangre para obtener valores de 3 biomarcadores relacionados con esta enfermedad, denominados biomarcador 1, 2 y 3, obteniendo valores diversos tanto para cada paciente, como para cada biomarcador. Contiene las siguiente variables: - Paciente: el numero consecutivo de los pacientes incluídos en la base. - Biomarcador_1: el valor obtenido en sangre de un biomarcador determinado. - Biomarcador_2: el valor obtenido en sangre de un segundo biomarcador determinado. - Biomarcador_3: el valor obtenido en sangre de un tercer biomarcador determinado. - Diagnostico: si el paciente es sano o enfermo.
Ejercicios curva ROC
Para cada uno de lso tres biomarcadores estime:
- curva ROC
- AUC
- Punto de corte óptimo
Curva ROC y regresión logística
Curva ROC y regresión logística
La curva ROC y la regresión logística están estrechamente relacionadas, especialmente en el contexto de evaluar modelos de clasificación binaria
La curva ROC se usa para evaluar la capacidad de un modelo de clasificación, como la regresión logística, para distinguir entre las dos clases (caso y control) en diferentes puntos de corte.
Curva ROC y regresión logística
- La regresión logística proporciona una probabilidad de clasificación.
- La curva ROC muestra el desempeño de la clasificación en diferentes puntos de corte.
- AUC ofrece una medida de la capacidad general de clasificación del modelo, lo cual es particularmente útil para comparar diferentes modelos.
Una de las formas que tenemos para evaluar unm modelo de regresión logística es a través de la curva ROC y el AUC
Ejercicio de práctica 1
Utilice la base de datos “pima.tr” para identificar variables asociadas a diabetes (type)
Ejercicio de práctica 1
Después de seleccionar variables mi modelo final fue:
modelo.final <- glm(formula = type ~ glu + age + ped +
bmi + npreg, family = "binomial",
data = Pima.tr)
summary(modelo.final)
Call:
glm(formula = type ~ glu + age + ped + bmi + npreg, family = "binomial",
data = Pima.tr)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -9.938059 1.541571 -6.447 1.14e-10 ***
glu 0.031809 0.006667 4.771 1.83e-06 ***
age 0.039286 0.020967 1.874 0.06097 .
ped 1.811417 0.661048 2.740 0.00614 **
bmi 0.079672 0.032649 2.440 0.01468 *
npreg 0.103142 0.064517 1.599 0.10989
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 256.41 on 199 degrees of freedom
Residual deviance: 178.47 on 194 degrees of freedom
AIC: 190.47
Number of Fisher Scoring iterations: 5Ejercicio de práctica 1
Evaluación del modelo
# Cargar la librería pROC
library(pROC)
# Calcular las probabilidades predichas usando el modelo
probabilidades <- predict(modelo.final, type = "response")
# Calcula las probabilidades predichas de que cada observación sea positiva (es decir, el valor predicho de type).
# Generar la curva ROC usando las probabilidades predichas y la variable dependiente real
roc_curve <- roc(Pima.tr$type, probabilidades)
# Graficar la curva ROC
plot(roc_curve, main = "Curva ROC para el Modelo Logístico", col = "blue")
# Calcular y mostrar el AUC
auc_value <- auc(roc_curve)
print(paste("AUC:", round(auc_value, 2)))Ejercicio de práctica 1
Evaluación del modelo
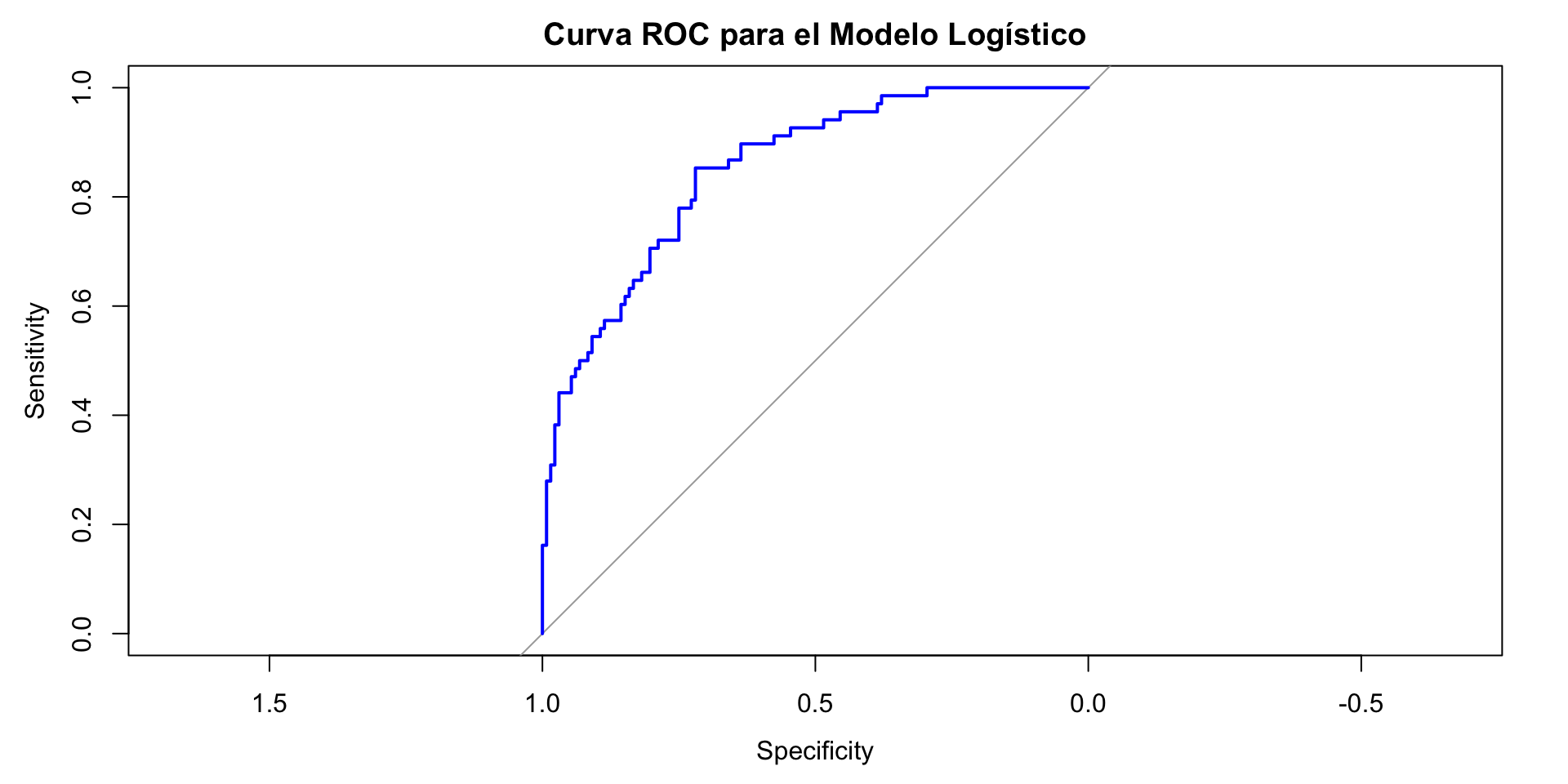
Ejercicio de práctica 1
Evaluación del modelo
[1] "AUC: 0.85"Ejercicio de práctica 1
Interpretación del resultado
El modelo tiene un buen desempeño, ya que el 85% del tiempo, el modelo asignará una mayor probabilidad al caso positivo (por ejemplo, un paciente con DM) que al negativo (paciente sin DM).
El AUC nos dice la capacidad del modelo para discriminar entre casos positivos y negativos en términos de probabilidades asignadas
Ejercicio de práctica 1
Interpretación del resultado
- AUC entre 0.7 y 0.8: El modelo tiene un desempeño aceptable.
- AUC entre 0.8 y 0.9: El modelo tiene un buen desempeño.
- AUC superior a 0.9: El modelo tiene un excelente desempeño
Ejercicios de tarea
Evaluar mediante AUC los modelos de regresión logística de tarea.
Bioestadística/Posgrados CUCS
Curvas ROC, AUC Y regresión logística Aspectos teóricos Edsaúl E. Pérez-Guerrero, PhD; edsaul.perezg@academicos.udg.mx 2024-11-20