Bab 5 Ukuran Pemusatan Data

Dalam era data yang terus berkembang, memahami ukuran pemusatan menjadi keterampilan penting dalam analisis data. Ukuran seperti mean, median, dan modus membantu menggambarkan karakteristik utama distribusi data dari rata-rata nilai hingga pola frekuensi tertinggi.

Bab ini memberikan pengantar konsep ukuran pemusatan dalam sains data, menggabungkan teori dan aplikasi praktis. Pembahasan meliputi peran ukuran pemusatan dalam eksplorasi data, studi kasus pada data dunia nyata, dan kaitannya dengan visualisasi seperti histogram densitas dan boxplot.

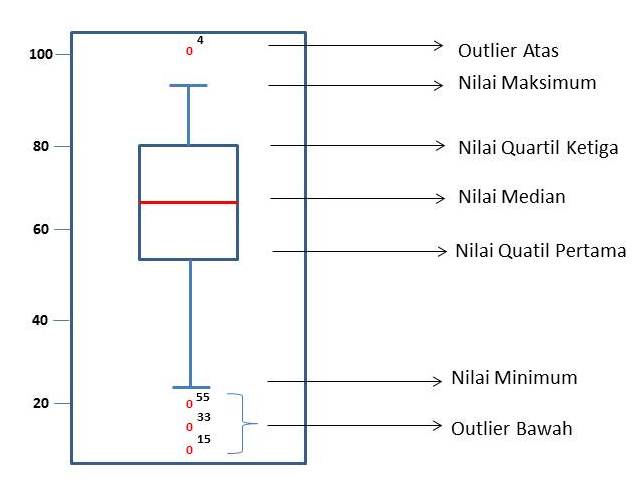
5.1 Definisi dan Konsep

Ukuran pemusatan adalah metode statistik yang digunakan untuk menentukan nilai yang mewakili pusat dari kumpulan data. Nilai ini membantu menggambarkan karakteristik umum data secara keseluruhan dan memberikan informasi tentang bagaimana data terdistribusi di sekitar titik tertentu.

5.2 Peran Ukuran Pemusatan

Ukuran pemusatan memiliki peran penting dalam statistik dan analisis data, terutama dalam menyederhanakan dan menyimpulkan informasi dari kumpulan data. Berikut adalah beberapa peran utama ukuran pemusatan data:

Peran	Penjelasan
Penyederhanaan	Ukuran pemusatan (mean, median, modus) memberikan gambaran umum data besar dengan satu nilai representatif.
Perbandingan	Memungkinkan perbandingan karakteristik utama antara beberapa kelompok data, seperti pendapatan antar wilayah.
Identifikasi Pola & Tren	Membantu mengenali kecenderungan atau pola data, berguna untuk memprediksi tren atau perubahan di masa depan.
Informasi Dasar	Menjadi dasar analisis statistik lanjutan, seperti perhitungan varians dan deviasi standar.
Pengambilan Keputusan	Digunakan untuk mendukung keputusan berbasis data, misalnya dalam menentukan strategi pemasaran berdasarkan rata-rata penjualan.
Mengatasi Keragaman	Median dan modus memberikan informasi yang lebih tepat daripada mean ketika data memiliki variasi besar atau outliers.

5.3 Mean (Rata-rata)

Mean (atau rata-rata) adalah ukuran pemusatan yang paling umum digunakan dalam statistik. Mean dihitung dengan menjumlahkan semua nilai dalam suatu kumpulan data, lalu membaginya dengan jumlah data yang ada. Mean memberikan gambaran umum tentang posisi pusat dari data.

Rumus untuk menghitung mean adalah sebagai berikut:

$\text{Mean} = \frac{\sum X}{n}$

dimana:

$\sum X$ adalah jumlah dari semua nilai data.
$n$ adalah jumlah data.

Langkah-langkah untuk menghitung mean:

Jumlahkan semua nilai dalam data.
Bagi hasil jumlah dengan banyaknya data.

Misalkan kita memiliki data sebagai berikut: 4, 5, 7, 8, 9.

Jumlahkan semua nilai: $4 + 5 + 7 + 8 + 9 = 33$
Bagi dengan jumlah data ( $n = 5$ ): $\text{Mean} = \frac{33}{5} = 6.6$

Jadi, mean dari data tersebut adalah 6.6.

5.3.1 Mean dalam Boxplot

# Memuat library
library(plotly)

# Data: dua skenario, satu dengan outliers, satu tanpa outliers
data_dengan_outliers <- c(5, 11, 12, 13, 14, 15, 16, 18,18, 19, 20, 22, 23, 55)  # Dengan outliers (5 dan 35)
data_tanpa_outliers <- c(10, 11, 12, 13, 14, 15, 16, 18,18, 19, 20, 22, 23, 24)          # Tanpa outliers

# Menghitung rata-rata untuk kedua dataset
mean_dengan_outliers <- mean(data_dengan_outliers)
mean_tanpa_outliers <- mean(data_tanpa_outliers)

# Menggabungkan data ke dalam satu data frame untuk visualisasi
data <- data.frame(
  Nilai = c(data_dengan_outliers, data_tanpa_outliers),
  Kelompok = rep(c("Dengan Outliers", "Tanpa Outliers"), 
                 times = c(length(data_dengan_outliers), length(data_tanpa_outliers)))
)

# Membuat boxplot menggunakan Plotly dengan outliers ditampilkan
plot <- plot_ly(
  data, 
  y = ~Nilai, 
  color = ~Kelompok, 
  type = "box", 
  boxpoints = "outliers"  # Menampilkan titik outliers
) %>%
  layout(
    title = "Pengaruh Outliers terhadap Mean",
    yaxis = list(title = "Nilai"),
    xaxis = list(title = "Kelompok"),
    annotations = list(
      list(
        x = "Dengan Outliers",
        y = mean_dengan_outliers,
        text = paste("Mean:", round(mean_dengan_outliers, 2)),
        showarrow = TRUE,
        arrowhead = 2
      ),
      list(
        x = "Tanpa Outliers",
        y = mean_tanpa_outliers,
        text = paste("Mean:", round(mean_tanpa_outliers, 2)),
        showarrow = TRUE,
        arrowhead = 2
      )
    )
  )

# Menampilkan plot
plot

5.3.2 Mean dalam Histogram

# Memuat library
library(plotly)

# Data: dua skenario, satu dengan outliers, satu tanpa outliers
data_dengan_outliers <- c(5, 11, 12, 13, 14, 15, 16, 18,18, 19, 20, 22, 23, 55)  # Dengan outliers (5 dan 35)
data_tanpa_outliers <- c(10, 11, 12, 13, 14, 15, 16, 18,18, 19, 20, 22, 23, 24)          # Tanpa outliers

# Membuat density plot untuk masing-masing dataset
density_dengan_outliers <- density(data_dengan_outliers)
density_tanpa_outliers <- density(data_tanpa_outliers)

# Pastikan tidak ada nilai negatif di x dan y
density_dengan_outliers$x <- pmax(0, density_dengan_outliers$x)
density_tanpa_outliers$x <- pmax(0, density_tanpa_outliers$x)

# Menghitung rata-rata
mean_dengan_outliers <- mean(data_dengan_outliers)
mean_tanpa_outliers <- mean(data_tanpa_outliers)

# Membuat plot menggunakan Plotly
plot <- plot_ly() %>%
  # Menambahkan density plot untuk dataset dengan outliers
  add_trace(
    x = ~density_dengan_outliers$x,
    y = ~density_dengan_outliers$y,
    type = 'scatter',
    mode = 'lines',
    name = "Dengan Outliers",
    line = list(color = 'rgba(222, 45, 38, 0.8)', width = 2)
  ) %>%
  # Menambahkan density plot untuk dataset tanpa outliers
  add_trace(
    x = ~density_tanpa_outliers$x,
    y = ~density_tanpa_outliers$y,
    type = 'scatter',
    mode = 'lines',
    name = "Tanpa Outliers",
    line = list(color = 'rgba(38, 166, 91, 0.8)', width = 2)
  ) %>%
  # Menambahkan garis rata-rata untuk dataset dengan outliers
  add_trace(
    x = c(mean_dengan_outliers, mean_dengan_outliers),
    y = c(0, max(density_dengan_outliers$y)),
    type = "scatter",
    mode = "lines",
    name = "Rata-rata (Dengan Outliers)",
    line = list(color = 'rgba(222, 45, 38, 0.6)', dash = 'dash')
  ) %>%
  # Menambahkan garis rata-rata untuk dataset tanpa outliers
  add_trace(
    x = c(mean_tanpa_outliers, mean_tanpa_outliers),
    y = c(0, max(density_tanpa_outliers$y)),
    type = "scatter",
    mode = "lines",
    name = "Rata-rata (Tanpa Outliers)",
    line = list(color = 'rgba(38, 166, 91, 0.6)', dash = 'dash')
  ) %>%
  layout(
    title = "Pengaruh Outliers terhadap Mean pada Density Plot",
    xaxis = list(title = "Nilai"),
    yaxis = list(title = "Kepadatan"),
    annotations = list(
      # Anotasi untuk rata-rata dataset dengan outliers
      list(
        x = mean_dengan_outliers,
        y = max(density_dengan_outliers$y) * 0.9,
        text = paste("Mean:", round(mean_dengan_outliers, 2)),
        showarrow = TRUE,
        arrowhead = 2,
        ax = 0,
        ay = -30,  # Posisi teks sedikit lebih tinggi dari garis
        font = list(color = 'rgba(222, 45, 38, 0.8)', size = 12)
      ),
      # Anotasi untuk rata-rata dataset tanpa outliers
      list(
        x = mean_tanpa_outliers,
        y = max(density_tanpa_outliers$y) * 0.9,
        text = paste("Mean:", round(mean_tanpa_outliers, 2)),
        showarrow = TRUE,
        arrowhead = 2,
        ax = 0,
        ay = -45,  # Posisi teks sedikit lebih tinggi dari garis
        font = list(color = 'rgba(38, 166, 91, 0.8)', size = 12)
      )
    )
  )

# Menampilkan plot
plot

5.4 Median

Median adalah nilai tengah dalam suatu kumpulan data yang telah diurutkan. Jika data terdiri dari jumlah yang ganjil, median adalah nilai yang tepat berada di tengah. Jika jumlah data genap, median dihitung sebagai rata-rata dari dua nilai tengah yang berurutan.

Rumus dan Cara Menghitung Median:

Langkah pertama: Urutkan data dari yang terkecil hingga yang terbesar.
Langkah kedua: Tentukan posisi median:
- Jika jumlah data ganjil, median adalah nilai di posisi tengah.
  - Posisi median = $\frac{n + 1}{2}$
- Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah.
  - Posisi median = $\frac{n}{2}$ dan $\frac{n}{2} + 1$
  - Median = $\frac{x_{\frac{n}{2}} + x_{\frac{n}{2} + 1}}{2}$

Contoh Perhitungan Median untuk Data Ganjil dan Genap

Contoh Data Ganjil: $5, 10, 12, 13, 15$

Urutkan data: $5, 10, 12, 13, 15$
Jumlah data = 5 (ganjil)
Posisi median = $\frac{5 + 1}{2} = 3$
Jadi, median adalah nilai ke-3, yaitu 12.

Contoh Data Genap: $7, 10, 12, 13, 14, 15$

Urutkan data: $7, 10, 12, 13, 14, 15$
Jumlah data = 6 (genap)
Posisi median: $\frac{6}{2} = 3$ dan $\frac{6}{2} + 1 = 4$
Median = $\frac{12 + 13}{2} = 12.5$

5.4.1 Median dalam Boxplot

5.4.2 Median dalam Histogram

5.5 Modus

Modus adalah nilai yang paling sering muncul dalam sebuah dataset. Modus digunakan untuk mengetahui nilai yang paling dominan atau paling sering terjadi dalam suatu kumpulan data. Modus bisa ditemukan dalam data kuantitatif maupun kategorikal.

Untuk mengidentifikasi modus dalam data, kita perlu mencari nilai yang memiliki frekuensi tertinggi. Untuk data numerik, modus bisa dihitung menggunakan frekuensi kemunculan masing-masing angka, sementara untuk data kategorikal, modus adalah kategori yang paling sering muncul.

Misalnya, kita memiliki data pengukuran tinggi badan berikut:

$5, 10, 12, 13, 15, 15, 16, 17, 20, 25, 28, 30, 35$

Untuk mencari modusnya, kita melihat nilai yang muncul paling sering. Dalam data di atas, angka 15 muncul tiga kali, sementara angka lainnya hanya muncul dua kali atau kurang. Oleh karena itu, modus dari data ini adalah 15.

Jika kita memiliki data kategorikal seperti warna favorit:

$Merah, Biru, Merah, Hijau, Merah, Biru$

Maka, modusnya adalah Merah, karena warna tersebut paling sering muncul.

5.5.1 Modus dalam Boxplot

5.5.2 Modus dalam Histogram

5.6 Perbandingan Mean, Median, dan Modus

Tabel berikut merangkum kelebihan, kekurangan, dan aplikasi utama dari mean, median, dan modus:

Aspek	Mean	Median	Modus
Definisi	Rata-rata aritmatika dari semua nilai dalam dataset.	Nilai tengah dari data yang diurutkan.	Nilai yang paling sering muncul dalam dataset.
Kelebihan	- Menggunakan semua data, mencerminkan keseluruhan dataset. - Cocok untuk data interval dan rasio.	- Tidak terpengaruh oleh outlier. - Cocok untuk data ordinal.	- Relevan untuk data kategorikal. - Mudah dihitung.
Kekurangan	- Rentan terhadap outlier (nilai ekstrem). - Tidak cocok untuk data distribusi tidak normal.	- Tidak mencakup keseluruhan informasi dataset. - Kurang stabil untuk data kecil.	- Tidak selalu ada modus (jika nilai sama frekuensinya). - Tidak menggunakan semua informasi dataset.
Penggunaan Utama	- Data simetris tanpa outlier. - Analisis kuantitatif seperti ekonomi atau keuangan.	- Data dengan distribusi tidak normal atau outlier.	- Data kategorikal seperti frekuensi preferensi pelanggan.
Ketahanan Terhadap Outlier	Sangat rentan terhadap outlier.	Tidak dipengaruhi oleh outlier.	Tidak dipengaruhi oleh outlier.
Contoh Aplikasi	- Menghitung rata-rata nilai ujian. - Rata-rata gaji karyawan.	- Median pendapatan rumah tangga di wilayah tidak merata.	- Menentukan ukuran pakaian yang paling sering dibeli.

Catatan:

Mean cocok digunakan untuk data yang terdistribusi normal.
Median sering digunakan untuk menggambarkan data yang tidak simetris.
Modus sangat berguna untuk data kategorikal atau nominal.

5.7 Praktikum 1

Buatkanlah penjelasan secara manual dan visualisasi ukuran Pemusatan untuk Data Kelompok, dengan sub-topik sebagai berikut:

5.7.1 Mean untuk Data Kelompok

5.7.2 Median untuk Data Kelompok

5.7.3 Modus untuk Data Kelompok

5.8 Praktikum 2

Carilah contoh sederhana yang menggukanakn Ukuran Pemusatan dalam Studi Kasus sebagai berikut:

Pengantar Statistik untuk Sains Data