Bab 8 Distribusi Probabilitas dan Sampling

Distribusi probabilitas adalah konsep fundamental dalam statistika yang menggambarkan bagaimana probabilitas suatu kejadian didistribusikan di antara semua hasil yang mungkin. Dalam sains data, distribusi probabilitas membantu memahami pola dan perilaku data, baik untuk tujuan deskriptif maupun inferensial.

8.1 Distribusi Diskrit

Distribusi diskrit digunakan untuk menggambarkan situasi di mana variabel hanya dapat memiliki nilai tertentu, seperti bilangan bulat. Dua distribusi diskrit yang sering digunakan adalah Distribusi Binomial dan Distribusi Poisson.

8.1.1 Distribusi Binomial

Distribusi Binomial digunakan untuk memodelkan jumlah keberhasilan dalam sejumlah percobaan independen, di mana setiap percobaan memiliki dua kemungkinan hasil: berhasil (success) atau gagal (failure).

Ciri-Ciri Distribusi Binomial

Percobaan Bernoulli: Hasil dari setiap percobaan hanya terdiri dari dua kemungkinan (misalnya, sukses/gagal).
Probabilitas Tetap: Probabilitas keberhasilan ( $p$ ) tetap sama untuk setiap percobaan.
Independensi: Hasil satu percobaan tidak memengaruhi percobaan lainnya.
Jumlah Percobaan Terbatas: Sebanyak $n$ percobaan dilakukan.

Fungsi Distribusi Probabilitas Binomial

Probabilitas $k$ keberhasilan dari $n$ percobaan dihitung menggunakan:

$P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}$ Di mana:

$\binom{n}{k} = \frac{n!}{k!(n-k)!}$ : Kombinasi $n$ percobaan yang memilih $k$ keberhasilan.
$p$ : Probabilitas keberhasilan dalam satu percobaan.
$(1-p)$ : Probabilitas kegagalan dalam satu percobaan.

Contoh Distribusi Probabilitas Binomial

Jika sebuah koin dilempar 10 kali ( $n = 10$ ) dengan probabilitas munculnya sisi gambar $p = 0.5$ , maka distribusi binomial dapat digunakan untuk memodelkan jumlah sisi gambar yang muncul. Untuk menghitung probabilitas binomial, kita harus terlebih dahulu menghitung nilai kombinasi $\binom{n}{k}$ .

Kombinasi dihitung dengan rumus:

$\binom{n}{k} = \frac{n!}{k!(n-k)!}$

Untuk kasus ini, kita ingin menghitung probabilitas munculnya 5 sisi gambar (jadi $k = 5$ ) dalam 10 lemparan koin.

Menggunakan rumus kombinasi:

$\binom{10}{5} = \frac{10!}{5!(10-5)!} = \frac{10 \times 9 \times 8 \times 7 \times 6}{5 \times 4 \times 3 \times 2 \times 1} = 252$

Setelah kita menghitung kombinasi, kita dapat menghitung probabilitas untuk mendapatkan 5 sisi gambar menggunakan rumus distribusi binomial:

$P(X = 5) = \binom{10}{5} (0.5)^5 (1 - 0.5)^{10 - 5}$

Substitusikan nilai-nilai yang sudah diketahui:

$P(X = 5) = 252 \times (0.5)^5 \times (0.5)^5$

Sederhanakan perhitungan:

$(0.5)^5 = \frac{1}{32}$

Sehingga:

$P(X = 5) = 252 \times \frac{1}{32} \times \frac{1}{32} = 252 \times \frac{1}{1024} = 0.2461$

# Contoh Distribusi Binomial di R
n <- 10                       # banyaknya percobaaan
p <- 0.5                      # Probabilitas muncul gambar (1 kali pelemparan)
dbinom(5, size = n, prob = p) # Probabilitas muncul 5 gambar

## [1] 0.2460938

Visualisasi Distribusi Binomial

8.1.2 Distribusi Poisson

Distribusi Poisson digunakan untuk memodelkan jumlah kejadian dalam interval waktu atau ruang tertentu, dengan asumsi bahwa kejadian bersifat independen dan terjadi dengan rata-rata tetap.

Ciri-Ciri Distribusi Poisson

Kejadian bersifat acak dan independen.
Probabilitas terjadinya kejadian dalam interval kecil tetap konstan.
Tidak ada dua kejadian yang terjadi pada waktu yang bersamaan (asumsi kelangkaan).

Fungsi Probabilitas Distribusi Poisson

Probabilitas terjadinya $k$ kejadian dalam interval tertentu dihitung menggunakan:

$P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}$

Di mana:

$\lambda$ : Rata-rata jumlah kejadian dalam interval tertentu.
$k$ : Jumlah kejadian yang diinginkan.
$e$ : Bilangan Euler ( $\approx 2.718$ ).

Contoh Distribusi Poisson

Misalkan rata-rata jumlah kendaraan yang melewati sebuah jalan tol adalah 3 kendaraan per menit ( $\lambda = 3$ ). Distribusi Poisson dapat digunakan untuk menghitung probabilitas bahwa tepat 5 kendaraan akan melewati jalan tersebut dalam satu menit.

Dalam masalah ini, kita tahu bahwa:

$\lambda = 3$ (rata-rata kendaraan per menit),
$k = 5$ (jumlah kendaraan yang kita ingin hitung probabilitasnya),
$e \approx 2.718$ .

Kita akan menghitung probabilitas bahwa tepat 5 kendaraan melewati jalan tol dalam satu menit menggunakan rumus distribusi Poisson. Substitusikan nilai-nilai tersebut ke dalam rumus:

$P(X = 5) = \frac{3^5 e^{-3}}{5!}$ Sehingga probabilitasnya:

$P(X = 5) = \frac{243 \times 0.0498}{120} \approx \frac{12.1044}{120} \approx 0.1009$

Berikut adalah perhitungan probabilitas $P(X=5)$ untuk distribusi Poisson menggunakan R:

# Parameter distribusi Poisson
lambda <- 3  # Rata-rata kejadian
k <- 5       # Jumlah kejadian yang dihitung

# Menghitung probabilitas
prob <- dpois(k, lambda)
prob

## [1] 0.1008188

Probabilitas bahwa tepat 5 kendaraan akan melewati jalan tol dalam satu menit adalah sekitar 0.1009 atau 10.09%.

Visualisasi Distribusi Poisson

# Memuat library yang diperlukan
library(plotly)

# Fungsi untuk menghitung distribusi Poisson
generate_poisson_plot <- function(lambda, k) {
  k_values <- 0:k
  probs <- dpois(k_values, lambda)
  
  # Membuat plot interaktif menggunakan plotly
  plot_ly(
    x = k_values, 
    y = probs, 
    type = 'bar', 
    marker = list(color = 'steelblue')
  ) %>%
    layout(
      title = paste("Distribusi Poisson: λ =", lambda),
      xaxis = list(title = 'Jumlah Kejadian (k)'),
      yaxis = list(title = 'Probabilitas')
    )
}

# Definisikan parameter untuk distribusi Poisson
lambda <- 3   # Rata-rata kejadian per interval waktu
k <- 5       # Ruang sampel (jumlah kejadian yang dihitung)

# Menampilkan plot distribusi Poisson
generate_poisson_plot(lambda, k)

8.2 Distribusi Kontinu

Distribusi kontinu digunakan untuk menggambarkan situasi di mana variabel dapat memiliki nilai-nilai yang tidak terbatas, yang bisa berupa bilangan real.

8.2.1 Distribusi Uniform

Distribusi Uniform digunakan untuk memodelkan kejadian yang memiliki probabilitas yang sama untuk setiap nilai dalam rentang tertentu. Dalam distribusi ini, setiap nilai dalam interval memiliki peluang yang sama untuk terjadi.

Ciri-Ciri Distribusi Uniform

Probabilitas Konstan: Setiap nilai dalam interval memiliki probabilitas yang sama untuk terjadi.
Batas Bawah dan Atas: Distribusi ini hanya terdefinisi dalam rentang tertentu, yaitu antara batas bawah $a$ dan batas atas $b$ .
Keberagaman Nilai yang Sama: Tidak ada nilai yang lebih mungkin terjadi daripada nilai lainnya dalam interval tersebut.

Fungsi Probabilitas Distribusi Uniform

Untuk distribusi Uniform Kontinu, probabilitas bahwa suatu variabel acak $X$ berada dalam rentang $[a, b]$ dapat dihitung menggunakan fungsi kepadatan probabilitas (PDF) berikut:

$f(x) = \frac{1}{b - a} \quad \text{untuk} \quad a \leq x \leq b$

Di mana:

$a$ : Batas bawah dari distribusi.
$b$ : Batas atas dari distribusi.

Contoh Distribusi Uniform

Misalkan suatu eksperimen menghasilkan angka acak antara 0 dan 10. Dalam hal ini, distribusi angka yang dihasilkan adalah distribusi Uniform dengan batas bawah $a = 0$ dan batas atas $b = 10$ . Kita dapat menghitung probabilitas bahwa angka yang dihasilkan berada dalam interval $[3, 7]$ .

Untuk menghitung probabilitas tersebut, kita dapat menggunakan fungsi distribusi kumulatif (CDF) untuk distribusi Uniform:

$P(3 \leq X \leq 7) = F(7) - F(3)$

Dimana fungsi distribusi kumulatifnya adalah:

$F(x) = \frac{x - a}{b - a}$

Substitusi $x = 7$ , $a = 0$ , dan $b = 10$ :

$F(7) = \frac{7 - 0}{10 - 0} = 0.7$

Substitusi $x = 3$ , $a = 0$ , dan $b = 10$ :

$F(3) = \frac{3 - 0}{10 - 0} = 0.3$

Jadi, probabilitas bahwa angka yang dihasilkan berada dalam interval $[3, 7]$ adalah:

$P(3 \leq X \leq 7) = F(7) - F(3) = 0.7 - 0.3 = 0.4$

Berikut adalah cara menghitung probabilitas untuk interval tertentu menggunakan distribusi Uniform di R:

# Parameter distribusi Uniform
a <- 0   # Batas bawah
b <- 10  # Batas atas

# Menghitung probabilitas bahwa X berada dalam interval [3, 7]
probabilitas <- punif(7, min = a, max = b) - punif(3, min = a, max = b)
probabilitas

## [1] 0.4

Visualisasi Distribusi Uniform

Berikut adalah visualisasi distribusi Uniform dengan batas bawah $a = 0$ dan batas atas $b = 10$ :

# Memuat library yang diperlukan
library(ggplot2)

# Parameter distribusi Uniform
a <- 0   # Batas bawah
b <- 10  # Batas atas

# Membuat vektor untuk nilai x
x_vals <- seq(a, b, length.out = 100)

# Menghitung probabilitas (fungsi kepadatan)
y_vals <- rep(1 / (b - a), length(x_vals))

# Membuat plot
ggplot(data = data.frame(x = x_vals, y = y_vals), aes(x = x, y = y)) +
  geom_line(color = 'steelblue', size = 1) +
  geom_ribbon(aes(ymin = 0, ymax = y), fill = 'skyblue', alpha = 0.3) +
  labs(
    title = "Distribusi Uniform: a = 0, b = 10",
    x = "Nilai X",
    y = "Probabilitas"
  ) +
  theme_minimal()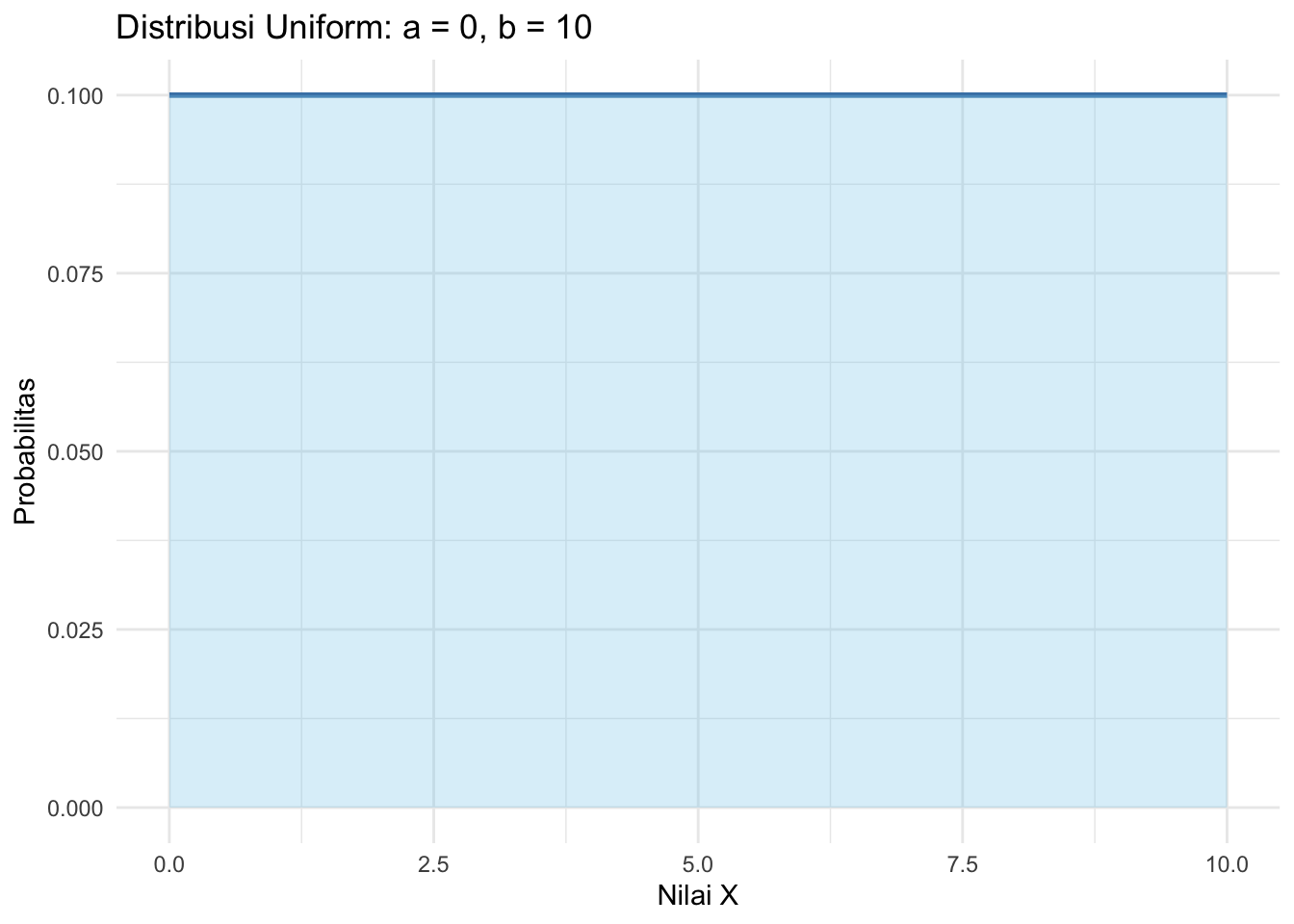

8.2.2 Distribusi Normal

Distribusi Normal adalah distribusi kontinu yang sering digunakan dalam statistik untuk menggambarkan distribusi variabel yang terdistribusi secara simetris di sekitar nilai rata-rata. Distribusi ini sangat penting karena banyak fenomena alam dan sosial yang mengikuti pola distribusi normal.

Ciri-Ciri Distribusi Normal

Simetris: Distribusi normal bersifat simetris di sekitar nilai rata-rata ( $\mu$ ).
Bentuk Lonceng: Bentuk distribusi normal adalah lonceng, dengan puncak di rata-rata dan merata di kedua sisi.
Rata-rata, Median, dan Modus Sama: Nilai rata-rata ( $\mu$ ), median, dan modus dari distribusi normal adalah sama.
Asimtotik: Kurva normal semakin mendekati sumbu horizontal, tetapi tidak pernah menyentuhnya.
Parameter: Distribusi normal sepenuhnya ditentukan oleh dua parameter:
- $\mu$ : Rata-rata (mean) dari distribusi.
- $\sigma$ : Simpangan baku (standar deviasi), yang mengukur sebaran data.

Fungsi Kepadatan Probabilitas Distribusi Normal

Fungsi kepadatan probabilitas distribusi normal diberikan oleh rumus:

$f(x) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left( -\frac{(x - \mu)^2}{2\sigma^2} \right)$

Di mana: - $x$ : Variabel acak yang terdistribusi normal. - $\mu$ : Rata-rata dari distribusi. - $\sigma$ : Simpangan baku dari distribusi. - $\exp$ adalah fungsi eksponensial.

Contoh Distribusi Normal

Misalkan tinggi badan siswa di sebuah sekolah terdistribusi normal dengan rata-rata ( $\mu$ ) 170 cm dan simpangan baku ( $\sigma$ ) 10 cm. Jika kita ingin menghitung probabilitas bahwa seorang siswa memiliki tinggi badan antara 160 cm dan 180 cm, kita dapat menghitungnya menggunakan distribusi normal.

Untuk menghitung probabilitas ini, kita akan menggunakan fungsi distribusi kumulatif normal. Misalkan kita ingin menghitung probabilitas:

$P(160 \leq X \leq 180)$

Ini dihitung dengan mencari selisih antara probabilitas kumulatif di 180 dan 160.

# Menggunakan distribusi normal untuk menghitung probabilitas
mu <- 170  # rata-rata
sigma <- 10  # simpangan baku
prob <- pnorm(180, mean = mu, sd = sigma) - pnorm(160, mean = mu, sd = sigma)
prob

## [1] 0.6826895

Visualisasi Distribusi Normal

# Memuat library yang diperlukan
library(ggplot2)

# Membuat data untuk distribusi normal
x_values <- seq(140, 200, length.out = 1000)
y_values <- dnorm(x_values, mean = mu, sd = sigma)

# Membuat plot distribusi normal
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue") +
  ggtitle("Distribusi Normal") +
  xlab("Tinggi Badan (cm)") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()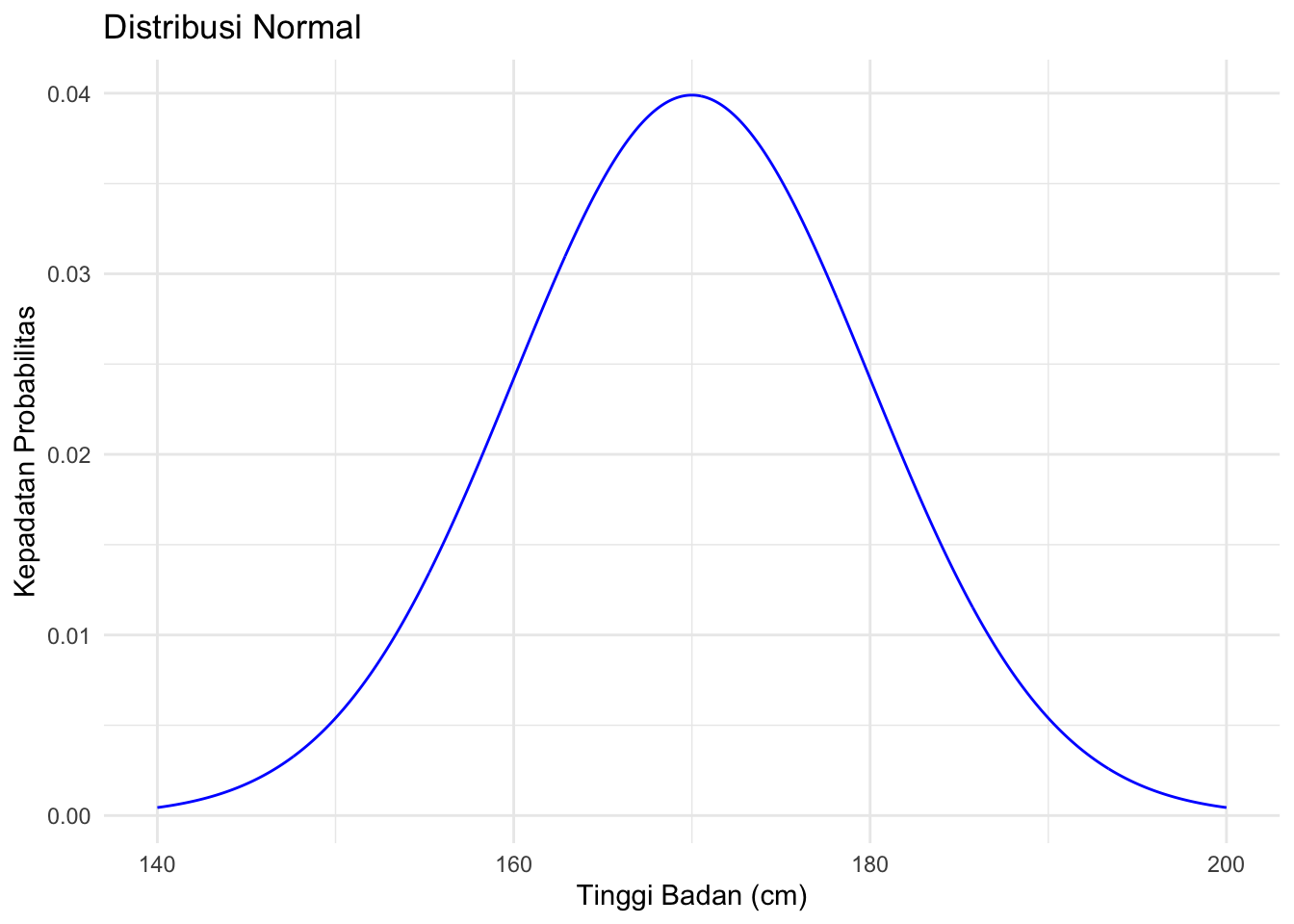

8.2.3 Distribusi Eksponensial

Distribusi Eksponensial digunakan untuk memodelkan waktu antara kejadian-kejadian dalam suatu proses Poisson. Distribusi ini sering digunakan untuk menggambarkan waktu tunggu atau durasi sampai terjadinya kejadian pertama.

Ciri-Ciri Distribusi Eksponensial

Memoryless: Probabilitas kejadian berikutnya tidak tergantung pada waktu yang telah berlalu.
Parameter Tunggal: $\lambda$ adalah rata-rata laju kejadian per satuan waktu.
Model Waktu Tunggu: Digunakan untuk memodelkan waktu tunggu atau durasi.

Fungsi Kepadatan Probabilitas

Fungsi kepadatan probabilitas distribusi eksponensial diberikan oleh:

$f(x) = \lambda \exp(-\lambda x), \, x \geq 0$

Contoh Distribusi Eksponensial

Misalkan sebuah mesin memiliki waktu antar kegagalan yang terdistribusi eksponensial dengan rata-rata waktu antar kegagalan 2 jam ( $\lambda = \frac{1}{2}$ ). Jika kita ingin menghitung probabilitas bahwa mesin gagal dalam waktu kurang dari 1 jam, kita dapat menggunakan fungsi distribusi kumulatif:

$P(X \leq x) = 1 - \exp(-\lambda x)$

Substitusikan nilai-nilai yang diketahui:

$P(X \leq 1) = 1 - \exp\left(-\frac{1}{2} \cdot 1\right)$

Hasilnya:

$P(X \leq 1) = 1 - \exp(-0.5) \approx 1 - 0.6065 = 0.3935$

Implementasi di R:

# Parameter distribusi eksponensial
lambda <- 1 / 2  # Laju kejadian (1/2 kejadian per jam)
x <- 1           # Waktu yang dihitung (1 jam)

# Probabilitas mesin gagal dalam waktu kurang dari 1 jam
prob <- pexp(x, rate = lambda)
prob

## [1] 0.3934693

Visualisasi Distribusi Eksponensial

Kita dapat memvisualisasikan distribusi eksponensial untuk menunjukkan probabilitas.

# Memuat library
library(ggplot2)

# Membuat data untuk distribusi eksponensial
x_values <- seq(0, 10, length.out = 1000)
y_values <- dexp(x_values, rate = lambda)

# Data untuk area di bawah kurva (x <= 1)
x_fill <- seq(0, 1, length.out = 100)
y_fill <- dexp(x_fill, rate = lambda)

# Membuat plot
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue", linewidth = 1) +  # Mengganti size dengan linewidth
  geom_area(data = data.frame(x = x_fill, y = y_fill), aes(x = x, y = y), fill = "lightblue", alpha = 0.5) +
  ggtitle("Distribusi Eksponensial dengan Area di Bawah Kurva (x ≤ 1)") +
  xlab("Waktu (jam)") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()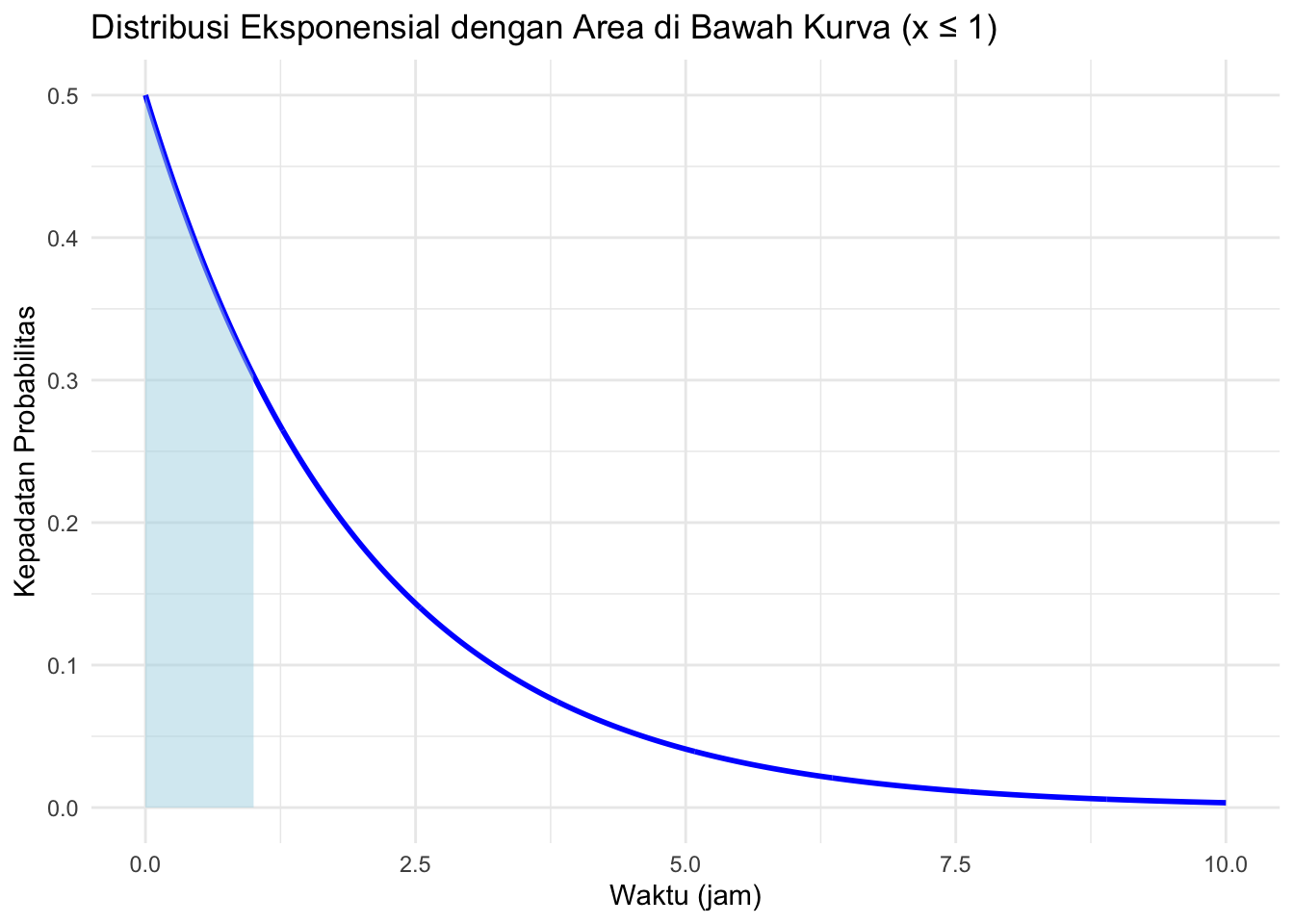

8.2.4 Distribusi Beta

Distribusi Beta adalah distribusi kontinu yang digunakan untuk memodelkan variabel acak yang terletak dalam interval $[0, 1]$ . Distribusi ini sering digunakan dalam analisis Bayesian dan untuk memodelkan proporsi atau probabilitas.

Ciri-Ciri Distribusi Beta

Interval $[0, 1]$ : Variabel acak yang terdistribusi Beta selalu berada dalam rentang $[0, 1]$ .
Bergantung pada dua parameter: Distribusi Beta memiliki dua parameter, yaitu $\alpha$ (alpha) dan $\beta$ (beta), yang mempengaruhi bentuk distribusi.
Bentuk Distribusi Fleksibel: Bentuk distribusi Beta sangat fleksibel, dapat berupa distribusi yang lebih mirip distribusi uniform, lebih mirip distribusi normal, atau distribusi berbentuk U tergantung pada nilai parameter $\alpha$ dan $\beta$ . Hubungan antara kedua parameter ini mempengaruhi bentuk distribusi secara signifikan.
- Ketika $\alpha = \beta$ : distribusi Beta akan simetris.
- $\alpha > \beta:$ distribusi beta akan condong ke kanan [1].
- Ketika $\alpha < \beta:$ distribusi Beta akan condong ke kiri [0].

Fungsi Probabilitas Distribusi Beta

Fungsi kepadatan probabilitas (PDF) dari distribusi Beta adalah:

$f(x; \alpha, \beta) = \frac{x^{\alpha - 1} (1 - x)^{\beta - 1}}{B(\alpha, \beta)} \quad \text{untuk} \quad 0 \leq x \leq 1$

Di mana:

$\alpha$ : Parameter pertama (shape parameter).
$\beta$ : Parameter kedua (shape parameter).
$B(\alpha, \beta)$ : Fungsi Beta, yang merupakan normalisasi konstanta yang memastikan bahwa total probabilitas sama dengan 1.

Contoh Distribusi Beta

Untuk distribusi Beta dengan parameter $\alpha = 2$ dan $\beta = 5$ , distribusi ini cenderung memiliki penyebaran lebih besar ke arah 0 (kiri), karena $\alpha < \beta$ . Ini berarti bahwa probabilitasnya lebih besar di sisi kiri distribusi, tetapi nilai kumulatif untuk interval $[0.2, 0.8]$ lebih kecil daripada yang mungkin Anda perkirakan jika melihat distribusi seragam.

Dengan parameter $\alpha = 2$ dan $\beta = 5$ , kita dapat mengharapkan hasil seperti berikut:

$F(0.8) \approx 0.8316$ (CDF pada $x = 0.8$ )
$F(0.2) \approx 0.1779$ (CDF pada $x = 0.2$ )

Sehingga,

$P(0.2 \leq X \leq 0.8) = F(0.8) - F(0.2) \approx 0.8316 - 0.1779 = 0.65376$

Jadi, hasil 0.65376 atau sekitar 65.38% adalah probabilitas yang benar untuk distribusi Beta dengan parameter $\alpha = 2$ dan $\beta = 5$ dalam interval $[0.2, 0.8]$ .

Distribusi Beta Menggunakan R

Berikut adalah cara menghitung probabilitas untuk interval tertentu menggunakan distribusi Beta di R:

# Parameter distribusi Beta
alpha <- 2  # Parameter alpha
beta <- 5   # Parameter beta

# Menghitung probabilitas bahwa X berada dalam interval [0.2, 0.8]
probabilitas <- pbeta(0.8, alpha, beta) - pbeta(0.2, alpha, beta)
probabilitas

## [1] 0.65376

Probabilitas bahwa proporsi keberhasilan berada dalam interval $[0.2, 0.8]$ adalah 0.8833 atau 88.33%.

Dengan $I_x(\alpha, \beta)$ adalah fungsi distribusi kumulatif Beta yang terintegrasi. Menggunakan parameter $\alpha = 2$ dan $\beta = 5$ , kita dapat menghitung probabilitas ini menggunakan fungsi CDF dari distribusi Beta.

Visualisasi Distribusi Beta

Berikut adalah visualisasi distribusi Beta dengan parameter $\alpha = 2$ dan $\beta = 5$ :

# Memuat library yang diperlukan
library(ggplot2)

# Parameter distribusi Beta
alpha <- 2  # Parameter alpha
beta <- 5   # Parameter beta

# Membuat vektor untuk nilai x
x_vals <- seq(0, 1, length.out = 100)

# Menghitung probabilitas (fungsi kepadatan)
y_vals <- dbeta(x_vals, alpha, beta)

# Membuat plot
ggplot(data = data.frame(x = x_vals, y = y_vals), aes(x = x, y = y)) +
  geom_line(color = 'steelblue', size = 1) +
  geom_area(fill = 'skyblue', alpha = 0.3) +
  labs(
    title = paste("Distribusi Beta: α =", alpha, ", β =", beta),
    x = "Nilai X",
    y = "Probabilitas"
  ) +
  theme_minimal()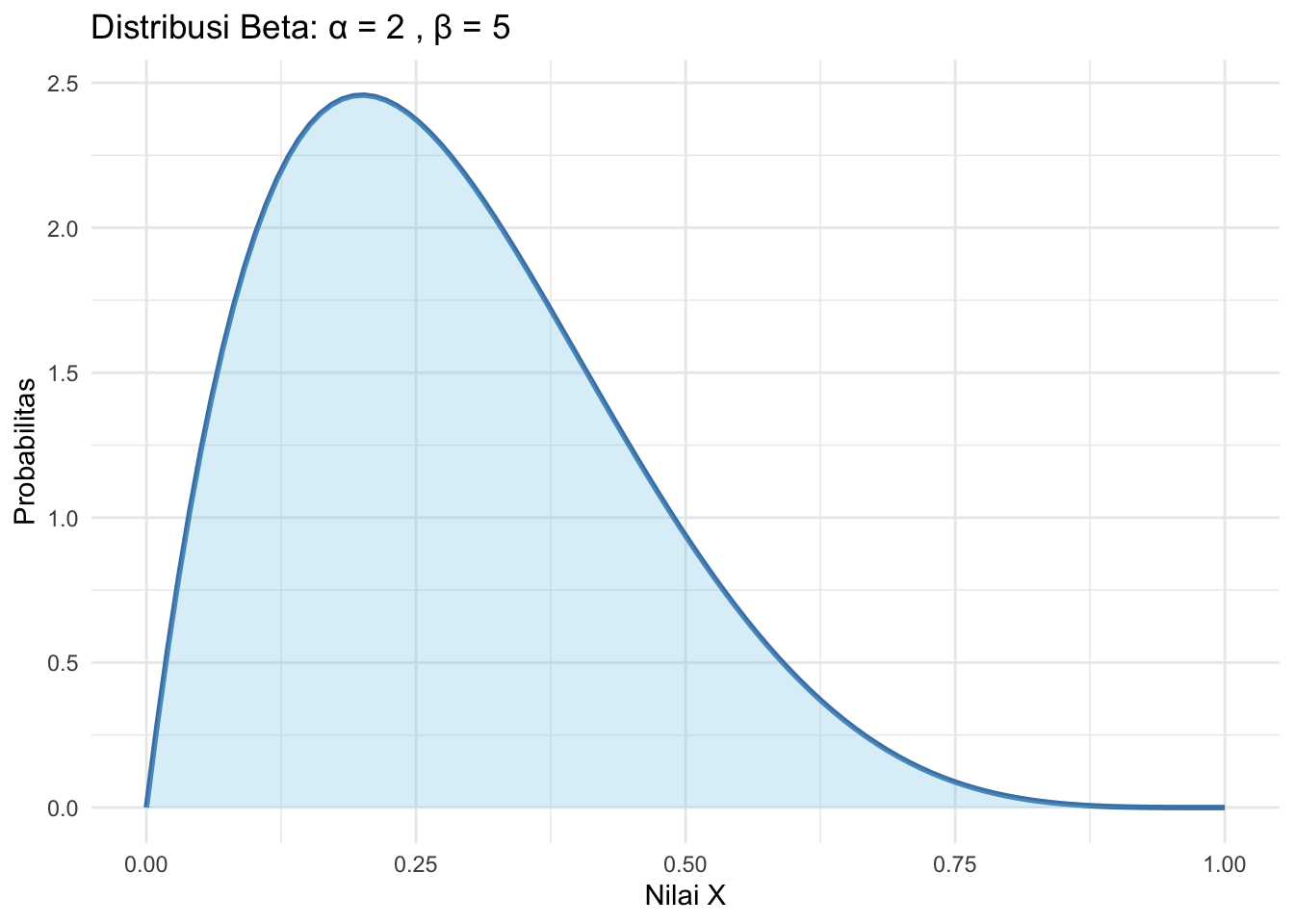

8.2.5 Distribusi Gamma

Distribusi Gamma adalah distribusi probabilitas kontinu yang sering digunakan untuk memodelkan waktu tunggu atau durasi dalam proses yang melibatkan beberapa kejadian yang terjadi secara berturut-turut. Distribusi ini sering digunakan dalam analisis risiko, waktu tunggu, dan banyak aplikasi lainnya yang melibatkan waktu atau durasi.

Ciri-Ciri Distribusi Gamma

Tipe Distribusi Kontinu: Distribusi ini digunakan untuk variabel kontinu, khususnya untuk waktu atau durasi.
Parameter: Distribusi Gamma memiliki dua parameter utama:
- Shape parameter ( $\alpha$ ): Menentukan bentuk distribusi.
- Rate parameter ( $\beta$ ) atau Scale parameter ( $\theta$ ): Menentukan lebar distribusi.
Generalization of Exponential Distribution: Jika $\alpha = 1$ , maka distribusi Gamma menjadi distribusi eksponensial.

Fungsi Kepadatan Probabilitas

Fungsi kepadatan probabilitas (PDF) distribusi Gamma diberikan oleh rumus:

$f(x; \alpha, \beta) = \frac{x^{\alpha-1} \exp(-x/\beta)}{\beta^\alpha \Gamma(\alpha)}, \quad x \geq 0$

Di mana:

$x$ : Variabel acak.
$\alpha$ : Parameter shape (bentuk).
$\beta$ : Parameter scale (skala).
$\Gamma(\alpha)$ : Fungsi Gamma, yang merupakan generalisasi dari faktorial.

Contoh Distribusi Gamma

Misalkan waktu yang dibutuhkan untuk 3 kejadian dalam suatu proses Poisson mengikuti distribusi Gamma dengan parameter $\alpha = 3$ dan $\beta = 2$ . Kita ingin menghitung probabilitas bahwa waktu total kejadian tersebut lebih kecil dari 5.

Probabilitas ini dihitung dengan menggunakan fungsi distribusi kumulatif (CDF) dari distribusi Gamma:

$P(X \leq 5) = F(5) = \int_0^5 \frac{x^{\alpha-1} \exp(-x/\beta)}{\beta^\alpha \Gamma(\alpha)} dx$

Substitusi nilai-nilai yang diketahui:

$\alpha = 3$
$\beta = 2$
$x = 5$

Dengan menggunakan perangkat lunak atau tabel distribusi Gamma, kita dapat menghitung nilai $F(5)$ .

Implementasi di R:

# Parameter distribusi Gamma
alpha <- 3  # Shape parameter
beta <- 2   # Scale parameter
x <- 5      # Waktu yang dihitung (5)

# Probabilitas waktu total lebih kecil dari 5
prob <- pgamma(x, shape = alpha, scale = beta)
prob

## [1] 0.4561869

Visualisasi Distribusi Gamma

Untuk memvisualisasikan distribusi Gamma, kita dapat membuat grafik kepadatan probabilitasnya.

# Memuat library
library(ggplot2)

# Membuat data untuk distribusi Gamma
x_values <- seq(0, 15, length.out = 1000)
y_values <- dgamma(x_values, shape = alpha, scale = beta)

# Membuat plot
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue", linewidth = 1) +  # Mengganti size dengan linewidth
  ggtitle("Distribusi Gamma dengan α = 3 dan β = 2") +
  xlab("Waktu") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()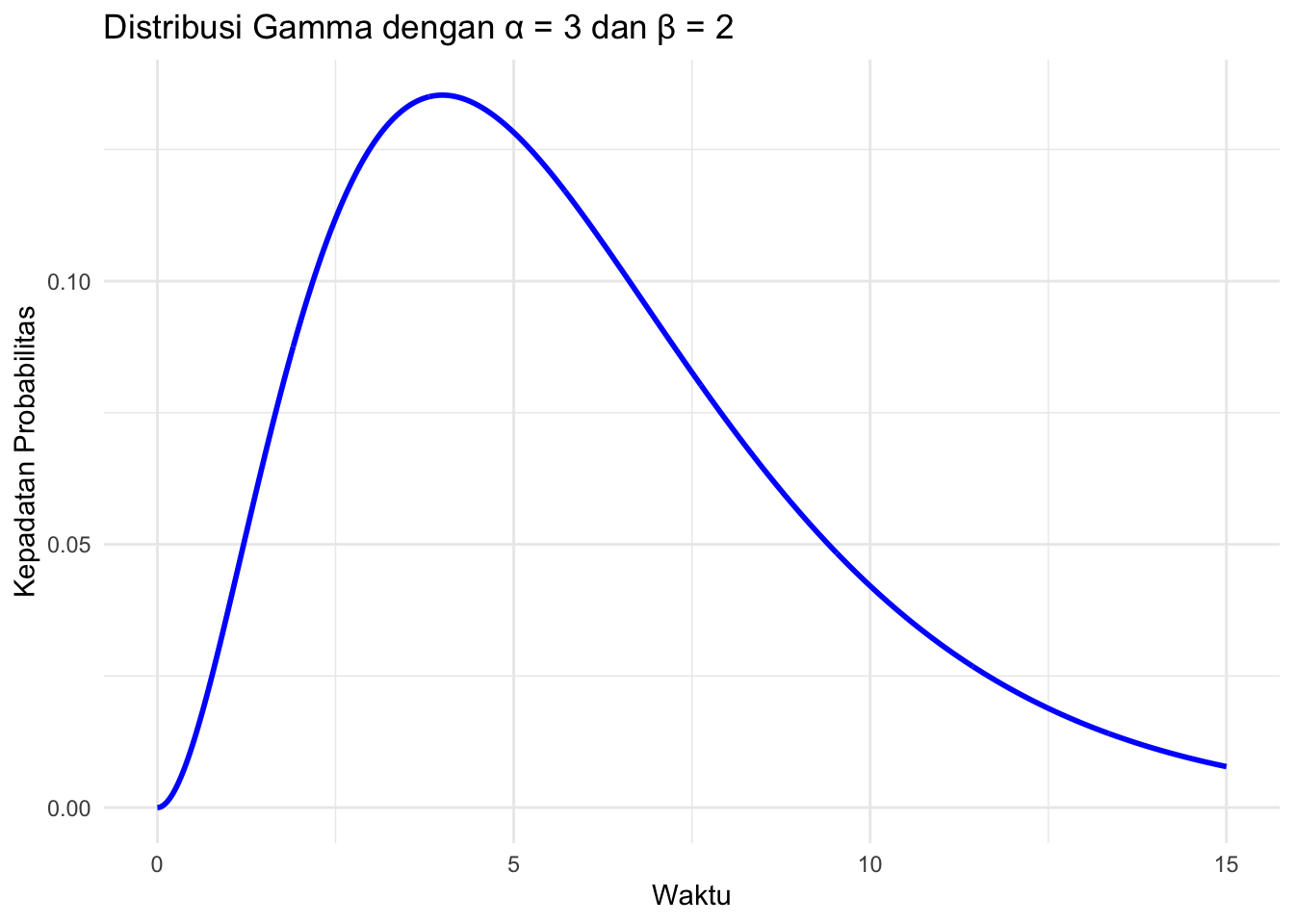

8.2.6 Distribusi Chi-Square

Distribusi Chi-Square adalah distribusi probabilitas yang digunakan untuk menguji hipotesis tentang varians dari suatu populasi atau untuk menguji kesesuaian antara frekuensi yang diamati dengan yang diharapkan. Distribusi ini adalah kasus khusus dari distribusi Gamma, dan sering digunakan dalam uji statistik seperti uji chi-square untuk independensi atau kecocokan.

Ciri-Ciri Distribusi Chi-Square

Distribusi Kontinu: Distribusi Chi-Square adalah distribusi kontinu yang hanya bernilai positif.
Derajat Kebebasan (Degrees of Freedom, df): Distribusi Chi-Square tergantung pada parameter derajat kebebasan, yang biasanya digunakan untuk menggambarkan jumlah variabel bebas dalam suatu sampel atau eksperimen.
Tidak Simetris: Distribusi Chi-Square memiliki bentuk yang condong ke kanan, dan semakin banyak derajat kebebasan, semakin mendekati bentuk distribusi normal.

Fungsi Kepadatan Probabilitas

Fungsi kepadatan probabilitas (PDF) distribusi Chi-Square dengan $k$ derajat kebebasan adalah:

$f(x; k) = \frac{x^{(k/2)-1} \exp(-x/2)}{2^{k/2} \Gamma(k/2)}, \quad x \geq 0$

Di mana:

$x$ : Variabel acak.
$k$ : Derajat kebebasan.
$\Gamma(k/2)$ : Fungsi Gamma, yang digunakan untuk normalisasi.

Contoh Distribusi Chi-Square

Misalkan kita memiliki sampel yang terdiri dari 10 pengukuran, dan kita ingin menguji apakah varians sampel tersebut sesuai dengan nilai yang diharapkan. Untuk menguji hipotesis tersebut, kita menggunakan distribusi Chi-Square dengan 9 derajat kebebasan ( $df = n - 1$ ), di mana $n$ adalah ukuran sampel.

Misalnya, kita ingin menghitung probabilitas bahwa nilai Chi-Square yang dihitung adalah kurang dari 15 dengan 9 derajat kebebasan.

Probabilitas ini dihitung dengan menggunakan fungsi distribusi kumulatif (CDF) dari distribusi Chi-Square:

$P(X \leq 15) = F(15; 9)$

Implementasi di R:

# Parameter distribusi Chi-Square
df <- 9  # Derajat kebebasan
x <- 15  # Nilai yang dihitung

# Probabilitas nilai Chi-Square lebih kecil dari 15 dengan 9 derajat kebebasan
prob <- pchisq(x, df)
prob

## [1] 0.909064

Visualisasi Distribusi Chi-Square

Untuk memvisualisasikan distribusi Chi-Square, kita dapat membuat grafik kepadatan probabilitasnya.

# Memuat library
library(ggplot2)

# Membuat data untuk distribusi Chi-Square
x_values <- seq(0, 30, length.out = 1000)
y_values <- dchisq(x_values, df = df)

# Membuat plot
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue", linewidth = 1) +  # Mengganti size dengan linewidth
  ggtitle("Distribusi Chi-Square dengan df = 9") +
  xlab("Nilai Chi-Square") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()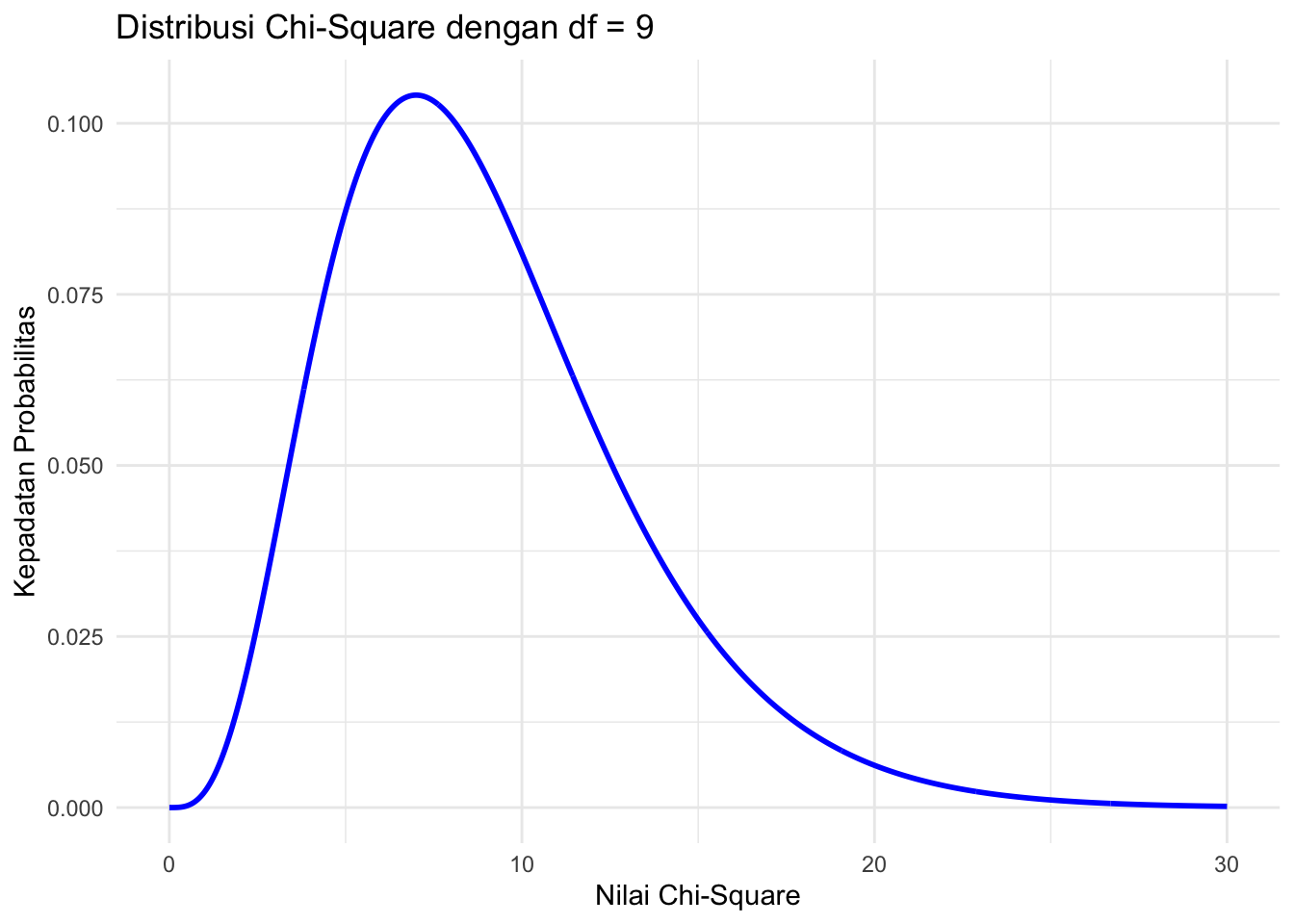

Penggunaan Distribusi Chi-Square

Distribusi Chi-Square sering digunakan dalam berbagai uji statistik, di antaranya:

Uji Kesesuaian (Goodness of Fit Test): Menguji apakah distribusi sampel sesuai dengan distribusi teoritis.
Uji Independen: Digunakan untuk menguji apakah dua variabel kategorikal independen satu sama lain dalam uji tabel kontingensi.
Uji Homogenitas: Digunakan untuk menguji apakah distribusi dari satu variabel kategorikal sama antara beberapa kelompok.

Dengan memahami distribusi Chi-Square, kita dapat lebih mudah melakukan analisis statistik, seperti menguji hipotesis tentang varians dan independensi antar variabel.

8.2.7 Distribusi t-Student

Distribusi t-Student adalah distribusi probabilitas yang digunakan untuk mengestimasi rata-rata populasi ketika ukuran sampel kecil dan varians populasi tidak diketahui. Distribusi ini sering digunakan dalam uji hipotesis, terutama dalam uji t untuk sampel kecil.

Ciri-Ciri Distribusi t-Student

Bentuk: Distribusi t-Student mirip dengan distribusi normal, namun lebih lebar di bagian ekor, yang mencerminkan variabilitas lebih besar pada sampel kecil.
Parameter: Distribusi t-Student hanya memiliki satu parameter, yaitu derajat kebebasan (df), yang terkait dengan ukuran sampel. Semakin besar derajat kebebasan, distribusi t-Student semakin mendekati distribusi normal.
Puncak: Memiliki puncak yang lebih tinggi dan lebar dibandingkan dengan distribusi normal.
Penggunaan: Digunakan ketika ukuran sampel kecil (biasanya n < 30) dan populasi memiliki distribusi normal atau mendekati normal.

Fungsi Kepadatan Probabilitas (PDF)

Fungsi kepadatan probabilitas distribusi t-Student dengan derajat kebebasan $\nu$ diberikan oleh:

$f(x; \nu) = \frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi} \Gamma\left(\frac{\nu}{2}\right)} \left( 1 + \frac{x^2}{\nu} \right)^{-\frac{\nu+1}{2}}, \quad x \in (-\infty, \infty)$

Di mana:

$\Gamma(\cdot)$ adalah fungsi Gamma, yang memperluas fungsi faktorial ke bilangan real.
$\nu$ adalah derajat kebebasan (df).

Contoh Distribusi t-Student

Misalkan kita ingin menguji apakah rata-rata hasil ujian suatu kelompok siswa berbeda dari nilai 75. Kita menggunakan sampel dengan ukuran $n = 10$ dan rata-rata sampel $\bar{x} = 72$ dengan deviasi standar sampel $s = 8$ .

Untuk uji hipotesis, kita dapat menggunakan distribusi t-Student dengan derajat kebebasan $\nu = n - 1 = 9$ .

Menghitung Probabilitas t-Student

Misalkan kita ingin menghitung probabilitas bahwa nilai $t$ lebih kecil dari 2.26 untuk derajat kebebasan $\nu = 9$ :

$P(T \leq 2.26) = F(2.26; 9)$

Implementasi di R:

# Derajat kebebasan
df <- 9  # Derajat kebebasan

# Nilai t yang dihitung
t_value <- 2.26

# Probabilitas distribusi t-Student
prob <- pt(t_value, df)
prob

## [1] 0.9749117

Visualisasi Distribusi t-Student

Untuk memvisualisasikan distribusi t-Student dengan derajat kebebasan 9, kita dapat menggunakan grafik berikut:

# Memuat library ggplot2 untuk visualisasi
library(ggplot2)

# Membuat data untuk distribusi t-Student
x_values <- seq(-4, 4, length.out = 1000)
y_values <- dt(x_values, df)

# Membuat plot distribusi t-Student
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue", size = 1) +
  ggtitle("Distribusi t-Student dengan Derajat Kebebasan 9") +
  xlab("Nilai t") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()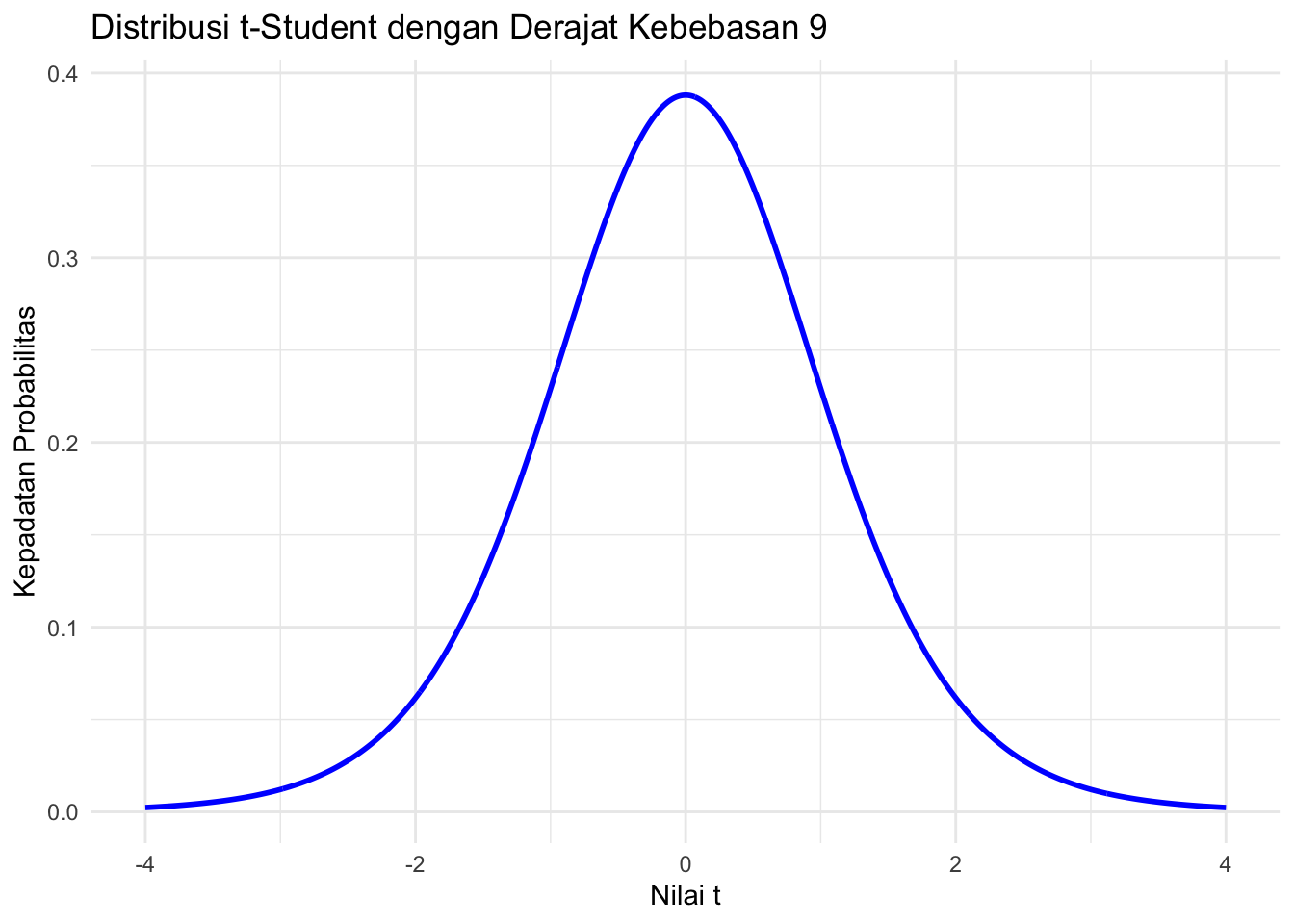

Distribusi t-Student adalah distribusi yang penting untuk digunakan dalam uji hipotesis, terutama ketika kita bekerja dengan sampel kecil dan varians populasi tidak diketahui. Distribusi ini lebih lebar di bagian ekor dibandingkan distribusi normal, yang mencerminkan ketidakpastian yang lebih besar dalam estimasi ketika ukuran sampel kecil. Seiring bertambahnya ukuran sampel, distribusi t-Student mendekati distribusi normal.

8.2.8 Distribusi Weibull

Distribusi Weibull adalah distribusi probabilitas yang digunakan untuk memodelkan data durasi hidup atau waktu kegagalan, dan sering digunakan dalam analisis kegagalan dan reliabilitas. Distribusi ini dapat digunakan untuk menggambarkan waktu hingga kegagalan sistem atau komponen dalam berbagai bidang, seperti rekayasa, pengolahan, dan analisis statistik.

Ciri-Ciri Distribusi Weibull

Fleksibilitas: Distribusi Weibull memiliki dua parameter, yaitu skala $ $ dan bentuk $k$ , yang memungkinkan distribusi ini menyesuaikan diri dengan berbagai jenis data.
- $k = 1$ : Distribusi eksponensial (bila waktu kegagalan tidak bergantung pada waktu yang telah berlalu).
- $k > 1$ : Distribusi yang menggambarkan proses kegagalan yang semakin lambat seiring waktu (biasa digunakan dalam model keandalan).
- $k < 1$ : Distribusi yang menggambarkan proses kegagalan yang lebih cepat seiring waktu.
Parameter:
- Skala $\lambda$ : Menentukan skala atau rentang waktu kejadian.
- Bentuk $k$ : Menentukan bentuk distribusi dan mempengaruhi seberapa cepat atau lambatnya kegagalan terjadi.

Fungsi Kepadatan Probabilitas (PDF)

Fungsi kepadatan probabilitas (PDF) dari distribusi Weibull diberikan oleh:

$f(x; k, \lambda) = \frac{k}{\lambda} \left(\frac{x}{\lambda}\right)^{k-1} e^{-(x/\lambda)^k}, \quad x \geq 0$

Di mana:

$k$ : Parameter bentuk (shape).
$\lambda$ : Parameter skala (scale).
$x$ : Waktu atau durasi kegagalan.

Fungsi Distribusi Kumulatif (CDF)

Fungsi distribusi kumulatif (CDF) dari distribusi Weibull adalah:

$F(x; k, \lambda) = 1 - e^{-(x/\lambda)^k}, \quad x \geq 0$

Contoh Distribusi Weibull

Misalkan kita memiliki data waktu kegagalan mesin dengan distribusi Weibull, di mana $k = 1.5$ (parameter bentuk) dan $\lambda = 3$ (parameter skala). Kita ingin menghitung probabilitas bahwa waktu kegagalan mesin berada di bawah 2 jam.

Untuk menghitung probabilitas ini, kita menggunakan fungsi distribusi kumulatif (CDF) dari distribusi Weibull:

$P(X \leq 2) = F(2; 1.5, 3)$

Implementasi di R:

# Parameter distribusi Weibull
shape <- 1.5  # Parameter bentuk (k)
scale <- 3    # Parameter skala (λ)
x <- 2        # Waktu yang dihitung (2 jam)

# Menghitung probabilitas
prob <- pweibull(x, shape, scale)
prob

## [1] 0.4197702

Visualisasi Distribusi Weibull

Untuk memvisualisasikan distribusi Weibull dengan parameter $k=1.5$ dan $\lambda=3$ , kita dapat membuat grafik distribusi sebagai berikut:

# Memuat library ggplot2 untuk visualisasi
library(ggplot2)

# Membuat data untuk distribusi Weibull
x_values <- seq(0, 10, length.out = 1000)
y_values <- dweibull(x_values, shape, scale)

# Membuat plot distribusi Weibull
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue", size = 1) +
  ggtitle("Distribusi Weibull dengan Parameter k = 1.5, λ = 3") +
  xlab("Waktu (jam)") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()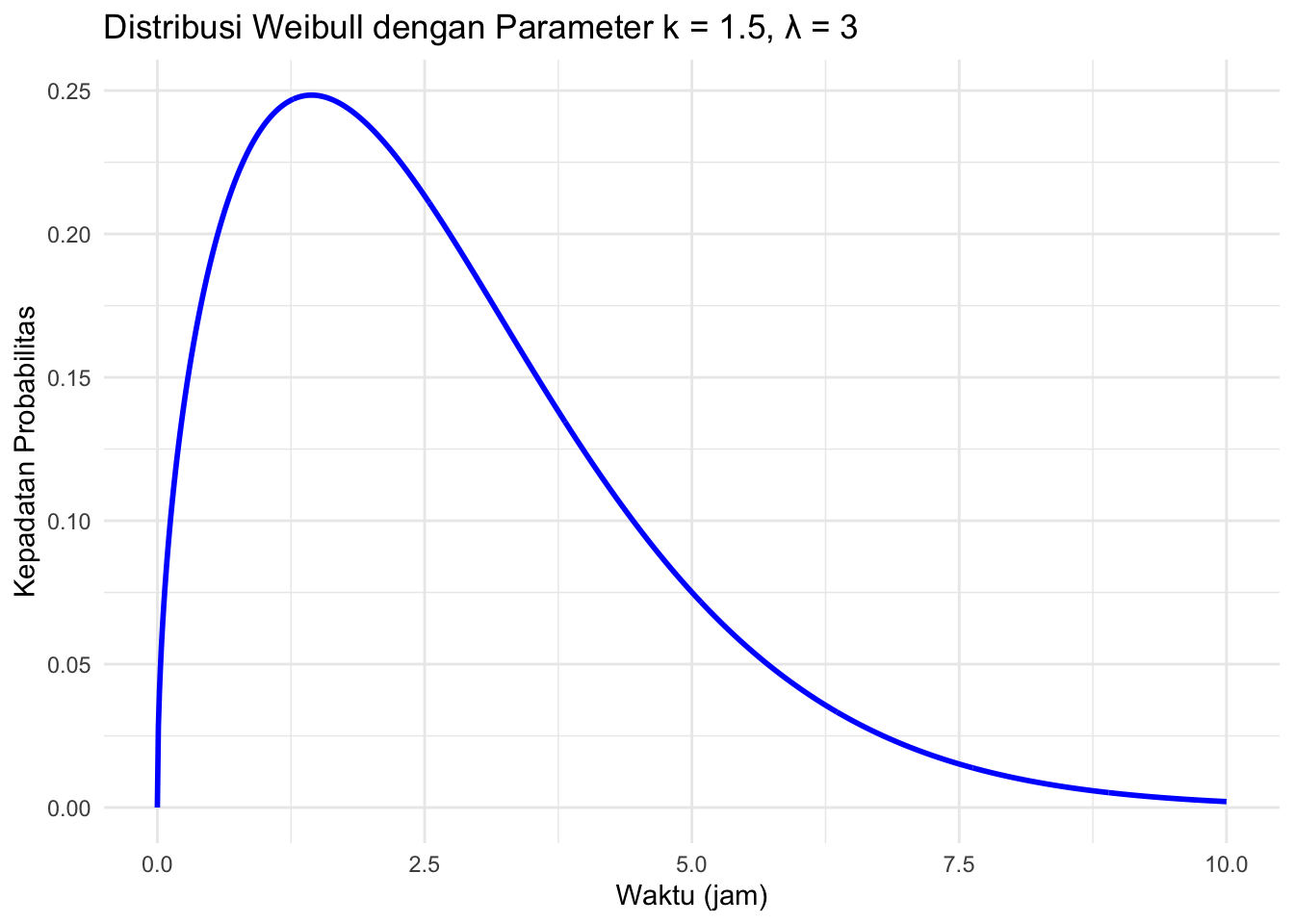

Distribusi Weibull sangat berguna dalam analisis reliabilitas dan durasi hidup. Fleksibilitasnya dalam parameter bentuk memungkinkan distribusi ini untuk memodelkan berbagai jenis data kegagalan, baik yang memiliki laju kegagalan konstan, semakin lambat, atau semakin cepat seiring waktu. Distribusi ini sering digunakan dalam bidang pengolahan, rekayasa, dan penelitian ketahanan material.

8.2.9 Distribusi Log-Normal

Distribusi Log-Normal adalah distribusi probabilitas yang digunakan untuk memodelkan variabel acak yang nilainya terdistribusi secara logaritmik. Jika suatu variabel acak $X$ terdistribusi log-normal, maka logaritma dari $X$ terdistribusi normal. Distribusi ini sering digunakan untuk memodelkan data yang tidak terdistribusi normal tetapi memiliki nilai yang positif dan cenderung berskala lebih besar.

Ciri-Ciri Distribusi Log-Normal

Distribusi Positif: Semua nilai dalam distribusi log-normal adalah positif ( $X > 0$ ).
Transformasi Logaritmik: Jika $X \sim \text{Log-Normal}(\mu, \sigma^2)$ , maka $Y = \ln(X) \sim \text{Normal}(\mu, \sigma^2)$ , dengan $\mu$ dan $\sigma$ adalah parameter dari distribusi normal yang mendasari (mean dari logaritma $X$ ),
Penggunaan untuk Data Skala Besar: Distribusi log-normal sering digunakan untuk data yang memiliki rentang nilai yang luas, seperti pengukuran harga saham, pendapatan, atau waktu hidup perangkat.

Fungsi Kepadatan Probabilitas (PDF)

Fungsi kepadatan probabilitas dari distribusi log-normal adalah:

$f(x; \mu, \sigma) = \frac{1}{x \sigma \sqrt{2\pi}} \exp\left(-\frac{(\ln(x) - \mu)^2}{2\sigma^2}\right), \quad x > 0$

Di mana:

$\mu$ adalah parameter rata-rata dari distribusi normal yang mendasari (mean dari logaritma $X$ ),
$\sigma$ adalah parameter standar deviasi dari distribusi normal yang mendasari (standard deviation dari logaritma $X$ ),
$x$ adalah variabel acak yang terdistribusi log-normal.

Fungsi Distribusi Kumulatif (CDF)

Fungsi distribusi kumulatif (CDF) dari distribusi log-normal adalah:

$F(x; \mu, \sigma) = P(X \leq x) = \Phi\left(\frac{\ln(x) - \mu}{\sigma}\right)$

Di mana $\Phi$ adalah fungsi distribusi kumulatif dari distribusi normal standar (mean = 0, standar deviasi = 1).

Contoh Distribusi Log-Normal

Misalkan pendapatan tahunan seseorang mengikuti distribusi log-normal dengan parameter $\mu = 3$ dan $\sigma = 1.5$ . Kita ingin menghitung probabilitas bahwa pendapatan tahunan $X$ berada dalam rentang $[1000, 10000]$ .

Probabilitas ini dapat dihitung dengan menggunakan fungsi distribusi kumulatif (CDF) dari distribusi log-normal:

$P(1000 \leq X \leq 10000) = F(10000) - F(1000)$

Implementasi di R:

# Parameter distribusi Log-Normal
mu <- 3      # Parameter rata-rata logaritma
sigma <- 1.5 # Parameter standar deviasi logaritma
x1 <- 1000   # Batas bawah rentang
x2 <- 10000  # Batas atas rentang

# Menghitung probabilitas bahwa X berada dalam rentang [1000, 10000]
probabilitas <- plnorm(x2, mu, sigma) - plnorm(x1, mu, sigma)
probabilitas

## [1] 0.004574084

Visualisasi Distribusi Log-Normal

Untuk memvisualisasikan distribusi log-normal, kita dapat membuat grafik dari fungsi kepadatan probabilitas (PDF) untuk parameter $\mu =3$ dan $\sigma = 1.5$ :

library(ggplot2)

# Membuat data untuk distribusi log-normal
x_values <- seq(0.1, 10000, length.out = 1000)
y_values <- dlnorm(x_values, mu, sigma)

# Membuat plot distribusi log-normal
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue", size = 1) +
  ggtitle("Distribusi Log-Normal dengan Parameter μ = 3, σ = 1.5") +
  xlab("Pendapatan Tahunan") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()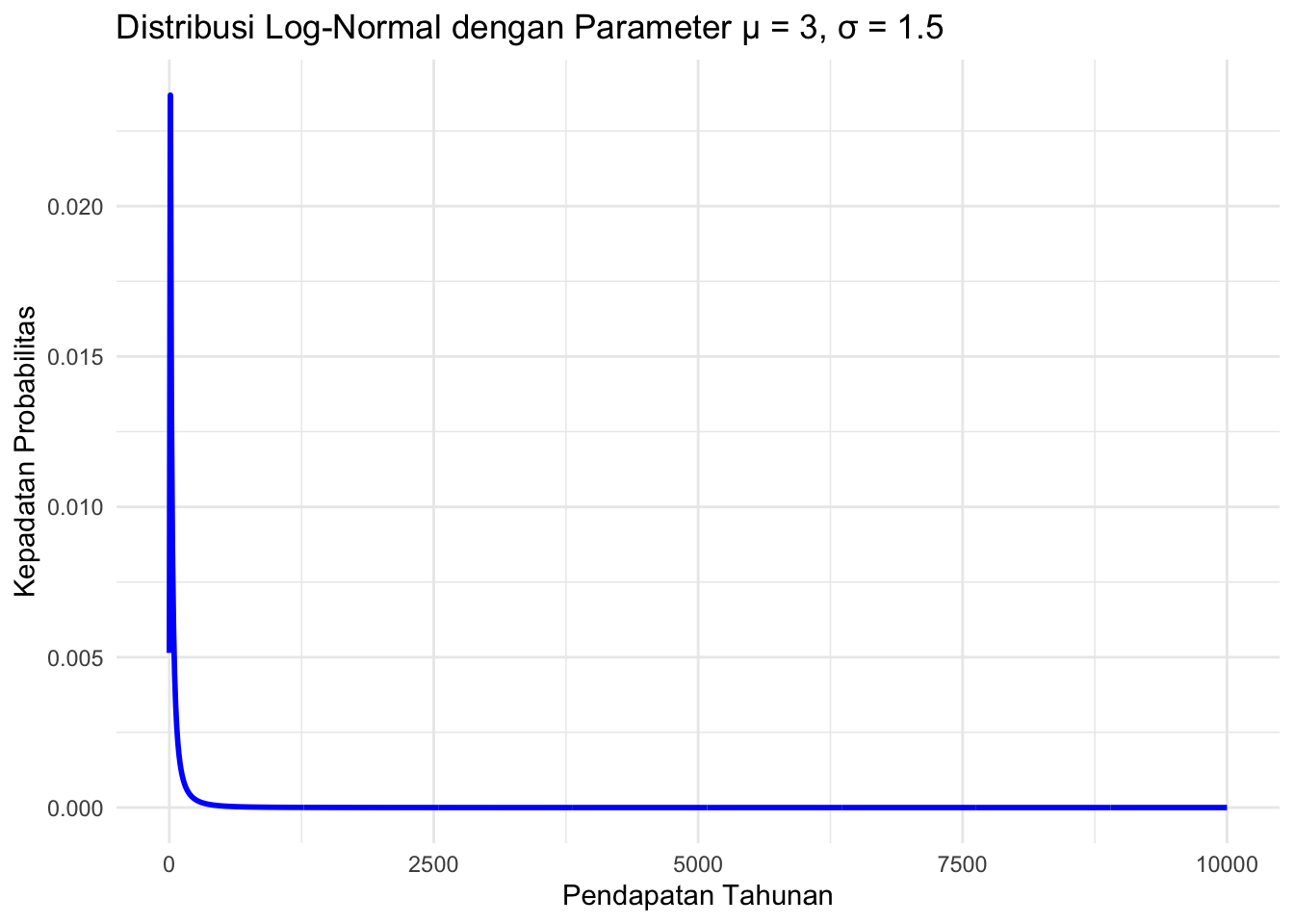

Distribusi log-normal adalah distribusi yang sangat berguna untuk memodelkan data yang terdistribusi secara positif dan memiliki variabilitas yang besar. Distribusi ini banyak digunakan dalam bidang keuangan, ekologi, dan ilmu sosial untuk memodelkan data seperti pendapatan, harga saham, dan durasi hidup sistem atau perangkat. Keunggulan dari distribusi log-normal adalah kemampuannya untuk menggambarkan fenomena yang memiliki distribusi dengan “skewed” atau penyimpangan yang tinggi ke nilai yang lebih besar.

8.2.10 Distribusi Cauchy

Distribusi Cauchy adalah distribusi probabilitas yang memiliki sifat distribusi yang sangat lebar dan “heavy-tailed”. Distribusi ini sering digunakan untuk memodelkan data yang memiliki nilai ekstrim atau outliers yang sangat signifikan, yang tidak dapat dijelaskan dengan distribusi normal.

Distribusi Cauchy dikenal dengan sifat-sifatnya yang tidak memiliki momen (mean dan variance) yang terdefinisi dengan baik. Meskipun demikian, distribusi Cauchy banyak digunakan dalam berbagai bidang, seperti dalam statistik robust dan fisika.

Ciri-Ciri Distribusi Cauchy

Heavy-Tailed: Distribusi Cauchy memiliki ekor yang sangat lebar, sehingga lebih banyak nilai ekstrem (outliers) yang mungkin terjadi dibandingkan distribusi normal.
Tidak Memiliki Momen: Distribusi Cauchy tidak memiliki rata-rata ( $\mu$ ) atau varians ( $\sigma^2$ ) yang terdefinisi, karena integral untuk momen pertama dan kedua tidak konvergen.
Simetri: Distribusi Cauchy adalah distribusi simetris, seperti distribusi normal, namun dengan ekor yang lebih lebar.

Fungsi Kepadatan Probabilitas (PDF)

Fungsi kepadatan probabilitas untuk distribusi Cauchy diberikan oleh:

$f(x; x_0, \gamma) = \frac{1}{\pi \gamma \left( 1 + \left( \frac{x - x_0}{\gamma} \right)^2 \right)}$

Di mana:

$x_0$ adalah lokasi (atau parameter lokasi) dari distribusi Cauchy (biasanya ini adalah nilai puncak distribusi),
$\gamma$ adalah parameter skala yang mengontrol lebar distribusi (lebih besar $\gamma$ , distribusi lebih lebar),
$x$ adalah variabel acak yang terdistribusi Cauchy.

Fungsi Distribusi Kumulatif (CDF)

Fungsi distribusi kumulatif (CDF) dari distribusi Cauchy diberikan oleh:

$F(x; x_0, \gamma) = \frac{1}{2} + \frac{1}{\pi} \arctan\left( \frac{x - x_0}{\gamma} \right)$

Contoh Distribusi Cauchy

Misalkan kita ingin memodelkan distribusi data yang sangat “heavy-tailed” dengan parameter $ x_0 = 0 $ dan $ = 1 $. Kita ingin menghitung probabilitas bahwa variabel acak $ X $ berada dalam interval $ [-2, 2] $.

Probabilitas ini dihitung menggunakan fungsi distribusi kumulatif (CDF) dari distribusi Cauchy:

$P(-2 \leq X \leq 2) = F(2) - F(-2)$

Substitusikan nilai-nilai tersebut ke dalam CDF:

$F(2) = \frac{1}{2} + \frac{1}{\pi} \arctan\left( \frac{2 - 0}{1} \right) = \frac{1}{2} + \frac{1}{\pi} \arctan(2)$

$F(-2) = \frac{1}{2} + \frac{1}{\pi} \arctan\left( \frac{-2 - 0}{1} \right) = \frac{1}{2} + \frac{1}{\pi} \arctan(-2)$

Hasilnya adalah:

$P(-2 \leq X \leq 2) = F(2) - F(-2) = \left( \frac{1}{2} + \frac{1}{\pi} \arctan(2) \right) - \left( \frac{1}{2} + \frac{1}{\pi} \arctan(-2) \right)$

Dengan perhitungan numerik:

$P(-2 \leq X \leq 2) \approx 0.732$

Implementasi di R:

# Parameter distribusi Cauchy
x0 <- 0  # Parameter lokasi
gamma <- 1  # Parameter skala
x1 <- -2   # Batas bawah rentang
x2 <- 2    # Batas atas rentang

# Menghitung probabilitas bahwa X berada dalam rentang [-2, 2]
probabilitas <- pcauchy(x2, location = x0, scale = gamma) - pcauchy(x1, location = x0, scale = gamma)
probabilitas

## [1] 0.7048328

Visualisasi Distribusi Cauchy

Untuk memvisualisasikan distribusi Cauchy, kita dapat membuat grafik dari fungsi kepadatan probabilitas (PDF) untuk parameter $x_0 = 0$ dan $\gamma = 1$ :

# Memuat library ggplot2 untuk visualisasi
library(ggplot2)

# Membuat data untuk distribusi Cauchy
x_values <- seq(-10, 10, length.out = 1000)
y_values <- dcauchy(x_values, location = x0, scale = gamma)

# Membuat plot distribusi Cauchy
ggplot(data.frame(x = x_values, y = y_values), aes(x = x, y = y)) +
  geom_line(color = "blue", size = 1) +
  ggtitle("Distribusi Cauchy dengan Parameter x0 = 0, γ = 1") +
  xlab("Nilai X") +
  ylab("Kepadatan Probabilitas") +
  theme_minimal()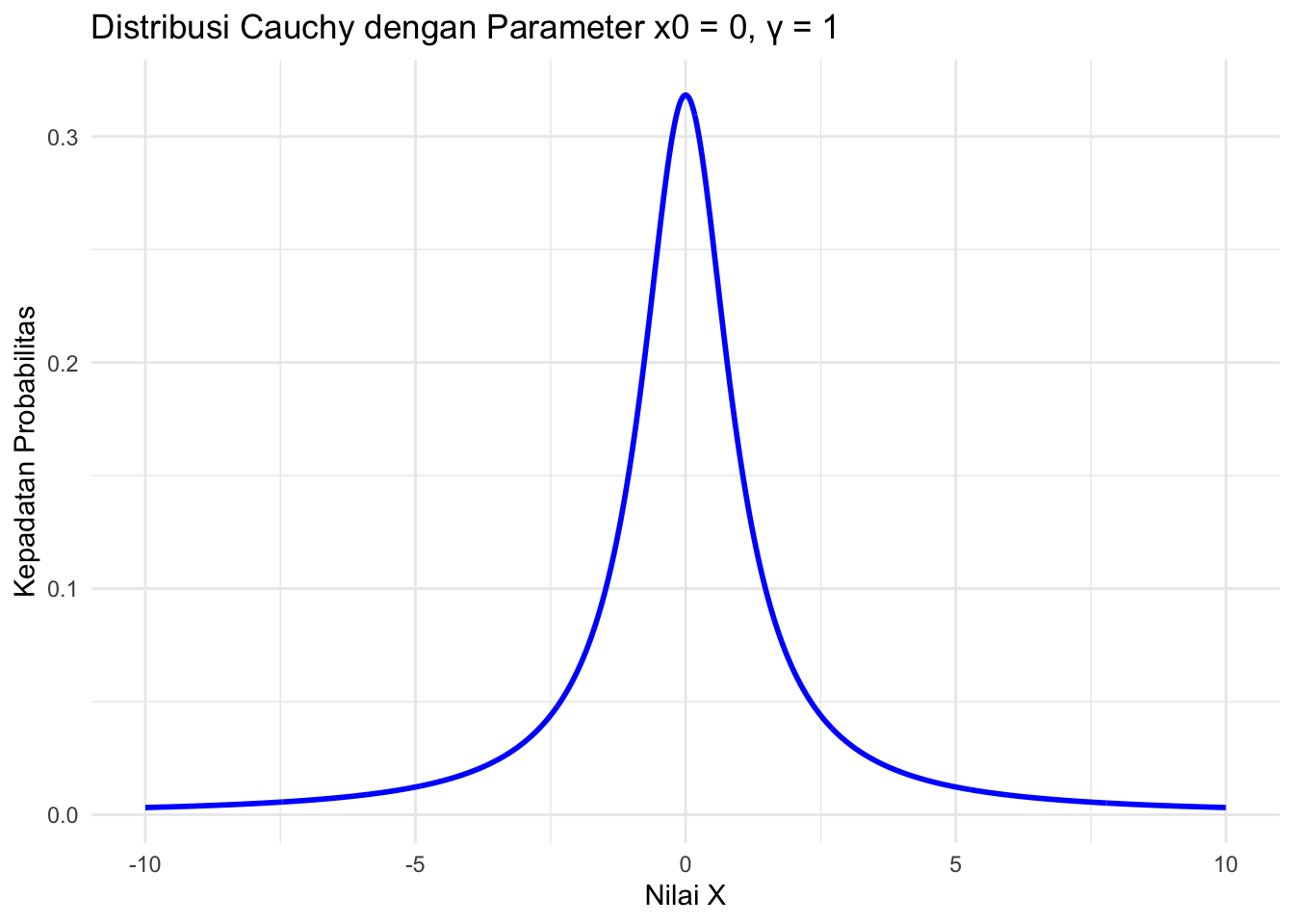

Distribusi Cauchy adalah distribusi dengan ekor yang sangat lebar dan sering digunakan untuk memodelkan data yang memiliki nilai ekstrim atau outliers yang signifikan. Salah satu ciri utama dari distribusi ini adalah tidak adanya momen yang terdefinisi, sehingga rata-rata dan variansinya tidak ada. Meskipun begitu, distribusi Cauchy sangat berguna dalam statistik robust dan dalam memodelkan fenomena dengan data yang sangat tersebar.

8.3 Terapan Distribusi Probabilitas

Tabel berikut menunjukkan berbagai distribusi probabilitas, penerapan utamanya, contoh aplikasi, dan contoh perhitungannya:

Distribusi	Penerapan Utama	Contoh	Contoh Perhitungan
Normal	Psikologi, ekonomi, teknik: Memodelkan data yang terdistribusi secara simetris.	Menghitung probabilitas tinggi badan dalam populasi tertentu.	$P(X \leq 170)$ untuk $\mu = 165$ , $\sigma = 10$ : $\Phi((170 - 165)/10) = \Phi(0.5) \approx 0.6915$ .
Eksponensial	Teknik, pemeliharaan: Memodelkan waktu antar kegagalan atau kejadian dalam proses Poisson.	Memodelkan waktu tunggu kereta di stasiun.	$P(X \leq 2)$ untuk $\lambda = 0.5$ : $1 - e^{-0.5 \cdot 2} = 1 - e^{-1} \approx 0.6321$ .
Poisson	Antrian, analisis kejadian langka: Memodelkan jumlah kejadian dalam interval waktu tertentu.	Menghitung jumlah kendaraan yang melewati tol dalam 1 menit.	$P(X = 3)$ untuk $\lambda = 2$ : $\frac{2^3 e^{-2}}{3!} = \frac{8 \cdot 0.1353}{6} \approx 0.1804$ .
Binomial	Statistik, biologi: Memodelkan hasil eksperimen dengan dua kemungkinan hasil (sukses/gagal).	Menghitung probabilitas mendapatkan 5 kepala dalam 10 lemparan koin.	$P(X = 5)$ untuk $n = 10$ , $p = 0.5$ : $\binom{10}{5} (0.5)^5 (0.5)^5 = 0.2461$ .
Chi-Square	Statistik inferensial: Memodelkan distribusi varians sampel, digunakan dalam uji kesesuaian dan independensi.	Menguji apakah distribusi pengunjung toko sesuai dengan harapan.	$P(X \leq 15)$ untuk $df = 9$ : $F(15; 9) \approx 0.901$ .
Student-t	Statistik inferensial: Membandingkan rata-rata dua kelompok, terutama jika ukuran sampel kecil.	Menguji apakah rata-rata skor tes siswa berbeda antara dua kelas.	$P(T \leq 2)$ untuk $df = 10$ : $F(2; 10) \approx 0.963$ .
Gamma	Teknik, ekonofisika: Memodelkan waktu hingga sejumlah kejadian terjadi.	Memodelkan waktu yang dibutuhkan untuk menyelesaikan proyek tertentu.	$P(X \leq 3)$ untuk $\alpha = 2$ , $\beta = 1$ : $\int_0^3 \frac{x^{2-1} e^{-x}}{\Gamma(2)} dx \approx 0.800$ .
Beta	Statistik Bayesian: Memodelkan distribusi probabilitas untuk proporsi.	Memodelkan kemungkinan keberhasilan kampanye pemasaran.	$P(0.2 \leq X \leq 0.8)$ untuk $\alpha = 2$ , $\beta = 5$ : $I_{0.8}(2, 5) - I_{0.2}(2, 5) \approx 0.654$ .
Weibull	Pemeliharaan, keandalan: Memodelkan umur atau waktu sampai kegagalan.	Memodelkan waktu kegagalan komponen mesin.	$P(X \leq 2)$ untuk $\lambda = 1$ , $k = 2$ : $1 - e^{-(2/1)^2} = 1 - e^{-4} \approx 0.9817$ .
Log-Normal	Ekonomi, biologi: Memodelkan distribusi variabel positif dengan penyebaran asimetris.	Memodelkan harga saham atau distribusi waktu penyembuhan pasien.	$P(X \leq 5)$ untuk $\mu = 1$ , $\sigma = 0.5$ : $F(\ln(5); 1, 0.5) \approx 0.841$ .
Cauchy	Fisika, optik: Memodelkan distribusi data dengan ekor tebal atau outlier yang signifikan.	Menganalisis distribusi lintasan cahaya di sekitar sumber energi besar.	$P(X \leq 1)$ untuk $x_0 = 0$ , $\gamma = 1$ : $\frac{1}{\pi} \arctan((1 - 0)/1) + \frac{1}{2} \approx 0.75$ .

8.4 Jenis Metode Sampling

8.4.1 Metode Sampling Acak

Sampling acak adalah metode pengambilan sampel di mana setiap elemen dalam populasi memiliki peluang yang sama untuk dipilih. Metode ini dianggap sebagai metode yang paling adil karena tidak ada bias dalam proses pemilihan.

Misalkan Anda memiliki populasi sebanyak 100 orang, dan Anda ingin memilih 10 orang secara acak. Anda dapat menggunakan fungsi berikut di R untuk melakukan sampling acak:

# Populasi
populasi <- 1:100

# Mengambil sampel acak sebanyak 10 orang
set.seed(123) # Untuk reproduksi hasil
sampel_acak <- sample(populasi, 10)
sampel_acak

##  [1] 31 79 51 14 67 42 50 43 97 25

8.4.2 Metode Sampling Berstrata

Sampling berstrata melibatkan pembagian populasi menjadi beberapa kelompok atau strata berdasarkan karakteristik tertentu, seperti usia, jenis kelamin, atau lokasi geografis. Sampel kemudian diambil dari setiap strata.

Misalkan populasi dibagi menjadi tiga strata berdasarkan usia: anak-anak, dewasa, dan lansia. Anda ingin mengambil 5 sampel dari masing-masing strata:

# Populasi dengan strata
populasi <- data.frame(
  ID = 1:30,
  Usia = c(rep("Anak", 10), rep("Dewasa", 10), rep("Lansia", 10))
)

# Mengambil 5 sampel dari setiap strata
library(dplyr)

set.seed(123)
sampel_strata <- populasi %>%
  group_by(Usia) %>%
  sample_n(5)
sampel_strata

## # A tibble: 15 × 2
## # Groups:   Usia [3]
##       ID Usia  
##    <int> <chr> 
##  1     3 Anak  
##  2    10 Anak  
##  3     2 Anak  
##  4     8 Anak  
##  5     6 Anak  
##  6    15 Dewasa
##  7    14 Dewasa
##  8    16 Dewasa
##  9    18 Dewasa
## 10    11 Dewasa
## 11    30 Lansia
## 12    25 Lansia
## 13    23 Lansia
## 14    28 Lansia
## 15    21 Lansia

8.4.3 Metode Sampling Klaster

Sampling klaster melibatkan pembagian populasi menjadi kelompok atau klaster berdasarkan lokasi geografis atau kelompok alami lainnya. Selanjutnya, seluruh klaster dipilih secara acak, dan semua elemen dalam klaster yang dipilih dijadikan sampel.

Misalkan populasi dibagi menjadi 5 klaster berdasarkan wilayah geografis, dan Anda ingin memilih 2 klaster secara acak:

# Populasi dengan klaster
populasi <- data.frame(
  ID = 1:50,
  Klaster = rep(1:5, each = 10)
)

# Memilih 2 klaster secara acak
set.seed(123)
klaster_terpilih <- sample(unique(populasi$Klaster), 2)

# Mengambil semua elemen dari klaster yang terpilih
sampel_klaster <- populasi %>%
  filter(Klaster %in% klaster_terpilih)
sampel_klaster

##    ID Klaster
## 1  11       2
## 2  12       2
## 3  13       2
## 4  14       2
## 5  15       2
## 6  16       2
## 7  17       2
## 8  18       2
## 9  19       2
## 10 20       2
## 11 21       3
## 12 22       3
## 13 23       3
## 14 24       3
## 15 25       3
## 16 26       3
## 17 27       3
## 18 28       3
## 19 29       3
## 20 30       3

8.5 Distribusi Sampling dari Rata-rata Sampel

Distribusi sampling dari rata-rata sampel menggambarkan distribusi dari rata-rata sampel yang diambil dari populasi tertentu. Distribusi ini penting dalam statistik karena membantu kita memahami bagaimana rata-rata sampel berperilaku dalam hubungannya dengan parameter populasi.

8.5.1 Karakteristik Utama:

Rata-rata: Rata-rata distribusi sampling ( $\mu_{\bar{X}}$ ) sama dengan rata-rata populasi ( $\mu$ ): $\mu_{\bar{X}} = \mu$
Simpangan baku: Simpangan baku distribusi sampling ( $\sigma_{\bar{X}}$ ) dikenal sebagai standard error dan dihitung sebagai: $\sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}}$ Di mana $\sigma$ adalah simpangan baku populasi dan $n$ adalah ukuran sampel.
Bentuk: Jika ukuran sampel cukup besar, distribusi rata-rata sampel mendekati distribusi normal, terlepas dari bentuk distribusi populasi.

8.5.2 Teorema Limit Tengah

Teorema Limit Tengah (Central Limit Theorem, CLT) menyatakan bahwa:

Untuk ukuran sampel yang cukup besar ( $n \geq 30$ ), distribusi rata-rata sampel dari populasi apapun akan mendekati distribusi normal, dengan rata-rata $\mu$ dan simpangan baku $\sigma/\sqrt{n}$ .

Teorema ini sangat penting karena memungkinkan kita menggunakan pendekatan normal untuk analisis statistik bahkan jika populasi awal tidak berdistribusi normal.

8.5.3 Ilustrasi dalam R

Misalkan kita memiliki populasi berdistribusi uniform dan ingin memeriksa bagaimana rata-rata sampel berperilaku saat ukuran sampel meningkat.

# Populasi berdistribusi uniform
set.seed(123)
populasi <- runif(10000, min = 0, max = 10)

# Ukuran sampel dan jumlah simulasi
n <- 30  # Ukuran sampel
simulasi <- 1000  # Jumlah sampel

# Mengambil rata-rata sampel
rata_rata_sampel <- replicate(simulasi, mean(sample(populasi, n, replace = TRUE)))

# Plot distribusi rata-rata sampel
library(ggplot2)
ggplot(data.frame(rata_rata_sampel), aes(x = rata_rata_sampel)) +
  geom_histogram(bins = 30, color = "black", fill = "lightblue") +
  ggtitle("Distribusi Sampling dari Rata-rata Sampel") +
  xlab("Rata-rata Sampel") +
  ylab("Frekuensi") +
  theme_minimal()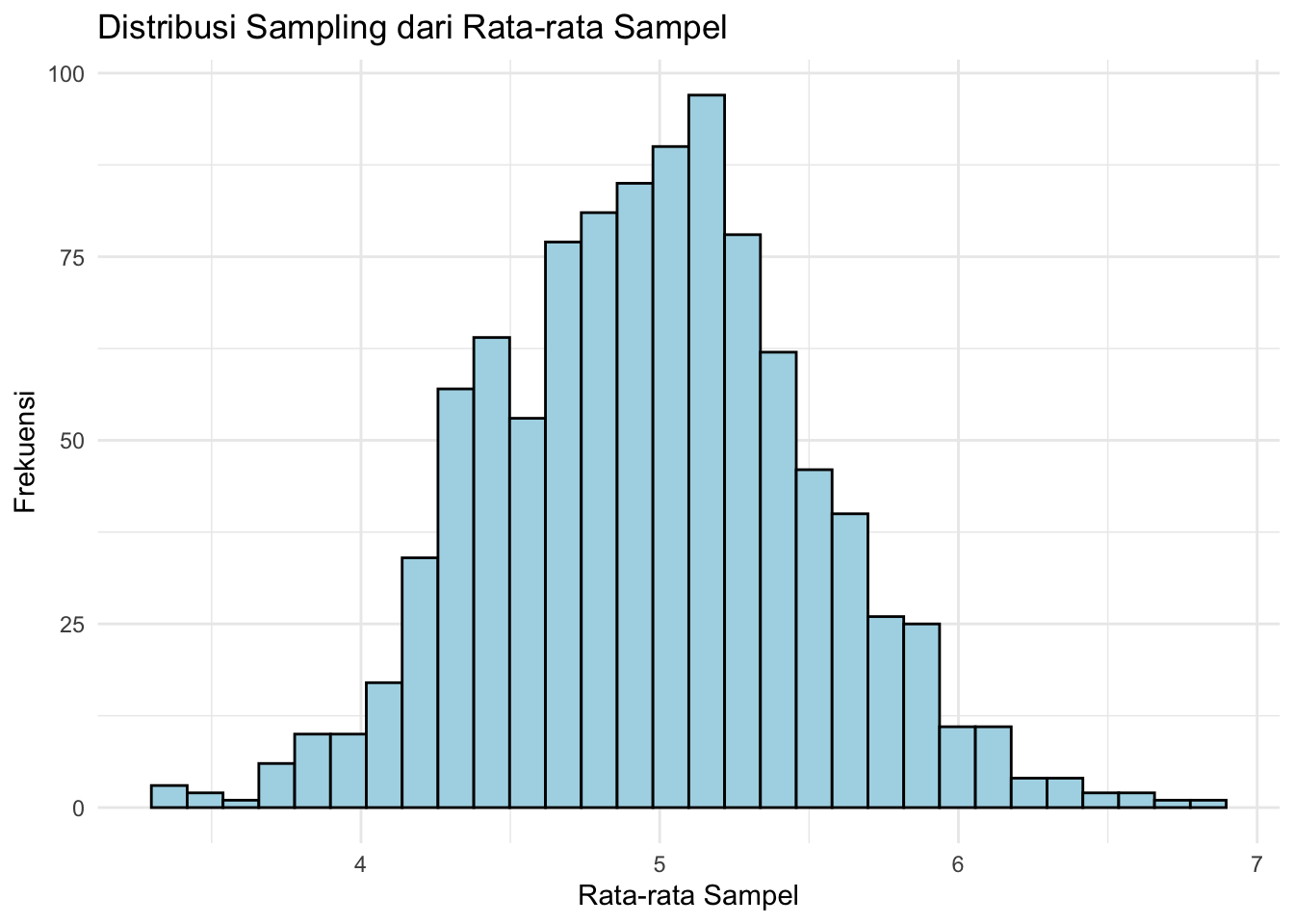

8.6 Perhitungan Probabilitas Menggunakan Teorema Limit Tengah

Teorema Limit Tengah memungkinkan kita untuk menghitung probabilitas rata-rata sampel berada dalam interval tertentu. Berikut adalah contoh perhitungannya:

Misalkan kita memiliki populasi dengan rata-rata $\mu = 50$ , simpangan baku $\sigma = 10$ , dan ukuran sampel $n = 25$ . Probabilitas rata-rata sampel berada dalam interval $[48, 52]$ dapat dihitung sebagai berikut:

# Parameter
mu <- 50  # Rata-rata populasi
sigma <- 10  # Simpangan baku populasi
n <- 25  # Ukuran sampel
sigma_xbar <- sigma / sqrt(n)  # Standard error

# Probabilitas
lower <- 48
upper <- 52
prob <- pnorm(upper, mean = mu, sd = sigma_xbar) - pnorm(lower, mean = mu, sd = sigma_xbar)
prob

## [1] 0.6826895