Bab 7 Konsep Dasar Probabilitas

Probabilitas adalah cabang ilmu Matematika yang digunakan untuk mengukur ketidakpastian. Dalam sains data, probabilitas adalah dasar dari metode inferensi statistik, pengambilan keputusan, dan pembelajaran mesin. Berikut materi lengkapnya:

7.1 Ruang Sampel dan Kejadian

7.1.1 Definisi Ruang Sampel

Ruang sampel (Sample Space, $S$) adalah kumpulan semua kemungkinan hasil dari suatu percobaan acak.

• Contoh 1: Melempar satu dadu, $S = \{1, 2, 3, 4, 5, 6\}$.
• Contoh 2: Melempar dua koin, $S = \{\text{GG}, \text{GA}, \text{AG}, \text{AA}\}$ (G = Gambar, A = Angka).

7.1.2 Definisi Kejadian

Kejadian ($A$) adalah subset dari ruang sampel, yaitu himpunan hasil tertentu yang menjadi fokus analisis.

• Contoh 1: Kejadian $A$ adalah “angka genap” saat melempar dadu, maka $Genap = \{2, 4, 6\}$.
• Contoh 2: Kejadian $B$ adalah “dua koin menunjukkan B,” maka $B = \{\text{KK}\}$.

7.2 Probabilitas Kejadian Tunggal

Jika semua hasil dalam ruang sampel memiliki peluang yang sama, probabilitas suatu kejadian $A$ dihitung sebagai:

$$P(A) = \frac{\text{Jumlah hasil yang memenuhi kejadian } A}{\text{Jumlah total hasil dalam ruang sampel}}$$

Perhatikan diagram venn berikut:

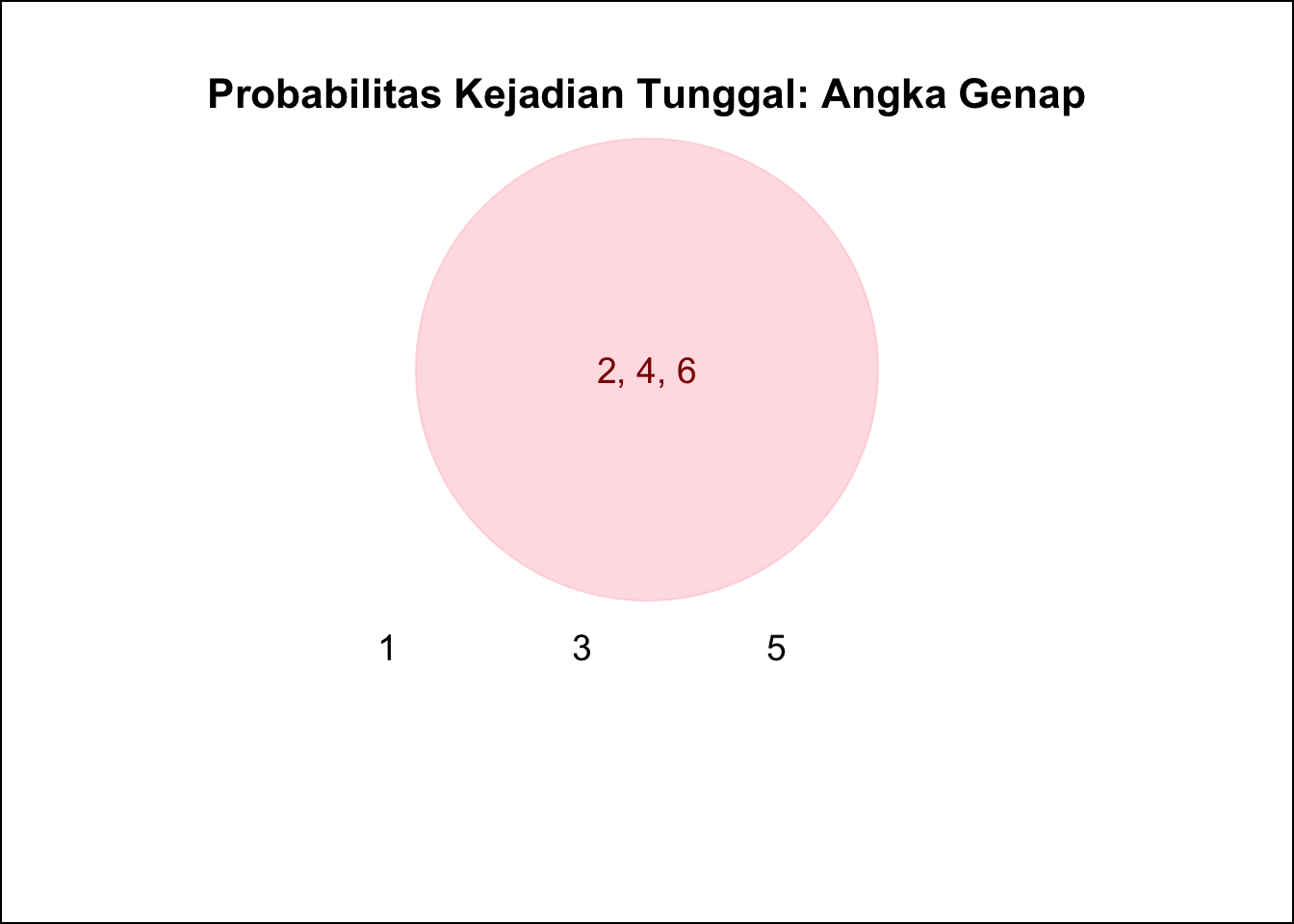
7.2.1 Contoh 1: Lemparan Koin

Ruang sampel: $\Omega = \{G, A\}$ (Gambar atau Angka).
Kejadian $A$: Mendapatkan Gambar ($Gambar = \{G\}$).

Probabilitas:

$$P(A) = \frac{\text{Jumlah hasil yang mendukung } A}{\text{Jumlah total hasil dalam } \Omega} = \frac{1}{2} = 0.5$$

7.2.2 Contoh 2: Lemparan Dadu

Ruang sampel: $\Omega = \{1, 2, 3, 4, 5, 6\}$.
Kejadian $A$: Mendapatkan angka genap ($A = \{2, 4, 6\}$).

Probabilitas:

$$P(A) = \frac{\text{Jumlah hasil yang mendukung } A}{\text{Jumlah total hasil dalam } \Omega} = \frac{3}{6} = 0.5$$

7.2.3 Contoh 3: Undian

Sebuah kotak berisi 10 bola, terdiri dari 7 bola merah dan 3 bola biru.
Kejadian $A$: Memilih bola merah.

Probabilitas:

$$P(A) = \frac{\text{Jumlah bola merah}}{\text{Jumlah total bola}} = \frac{7}{10} = 0.7$$

7.3 Probabilitas Saling Eksklusif

Probabilitas gabungan dari dua kejadian saling eksklusif adalah peluang bahwa salah satu dari kedua kejadian tersebut terjadi, tetapi tanpa adanya irisan antara keduanya. Jika dua kejadian saling eksklusif, maka kemungkinan keduanya terjadi bersamaan adalah nol, yaitu:

$$P(A \cap B) = 0$$

Dalam hal ini, rumus untuk probabilitas gabungan $P(A \cup B)$ menjadi lebih sederhana:

$$P(A \cup B) = P(A) + P(B)$$

Mari kita ambil contoh pelemparan sebuah dadu. Misalkan kita memiliki dua kejadian:

• Kejadian A: Muncul angka 1 pada pelemparan dadu pertama.
• Kejadian B: Muncul angka 6 pada pelemparan dadu kedua.

Kedua kejadian ini saling eksklusif, karena angka 1 pada dadu pertama dan angka 6 pada dadu kedua tidak bisa muncul bersamaan pada satu pelemparan.

Langkah-langkah untuk menghitung probabilitas gabungan:

7.3.1 $P(A)$

Probabilitas kejadian A adalah muncul angka 1 pada pelemparan dadu pertama. Pada pelemparan dadu, peluang muncul angka 1 adalah:

$$P(A) = \frac{1}{6} \quad \text{(karena ada 6 sisi pada dadu)}$$

7.3.2 $P(B)$

Probabilitas kejadian B adalah muncul angka 6 pada pelemparan dadu kedua. Peluang muncul angka 6 adalah:

$$P(B) = \frac{1}{6} \quad \text{(karena ada 6 sisi pada dadu)}$$

7.3.3 $P(A \cup B)$

Karena kejadian A dan B saling eksklusif, maka $P(A \cap B) = 04.$ Maka, probabilitas gabungan $P(A \cup B)$ adalah:

$$P(A \cup B) = P(A) + P(B) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}$$

Karena kejadian A dan B saling eksklusif, maka probabilitas gabungan $P(A \cup B)$ adalah:

$$P(A \cup B) = \frac{1}{3}$$

Artinya, peluang bahwa pada pelemparan dua dadu, muncul angka 1 pada dadu pertama atau angka 6 pada dadu kedua adalah $\frac{1}{3}$ atau sekitar 33.33%.

## Loading required package: futile.logger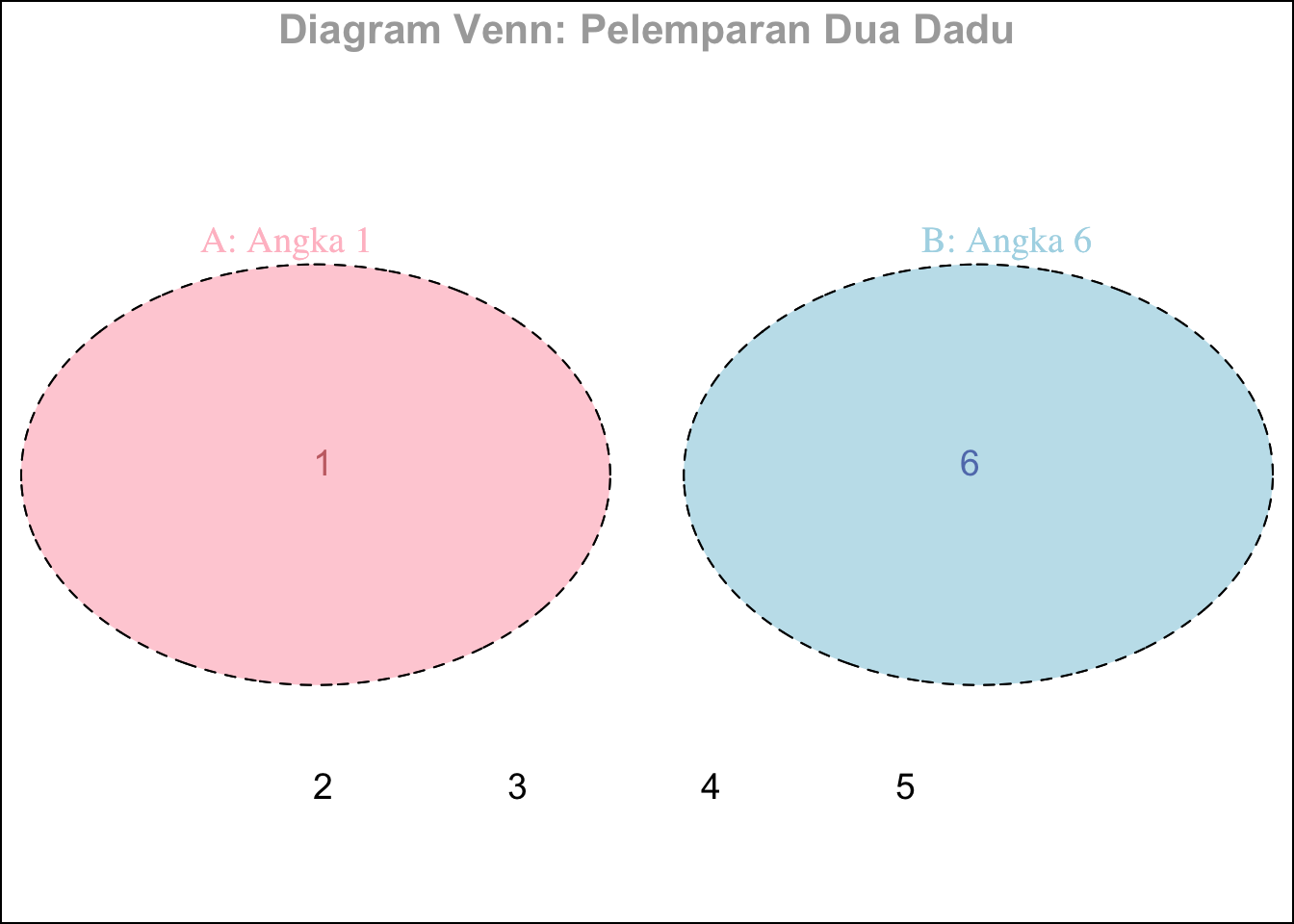

7.4 Probabilitas Tidak Saling Eksklusif

Probabilitas Gabungan (Tidak Saling Eksklusif) mencakup semua hasil dalam kejadian $A$, $B$, atau keduanya. Rumusnya:

$$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

Andaikan dilakukan pelemparan sebuah dadu, diperlihatkan dalam diagram sebagai berikut:

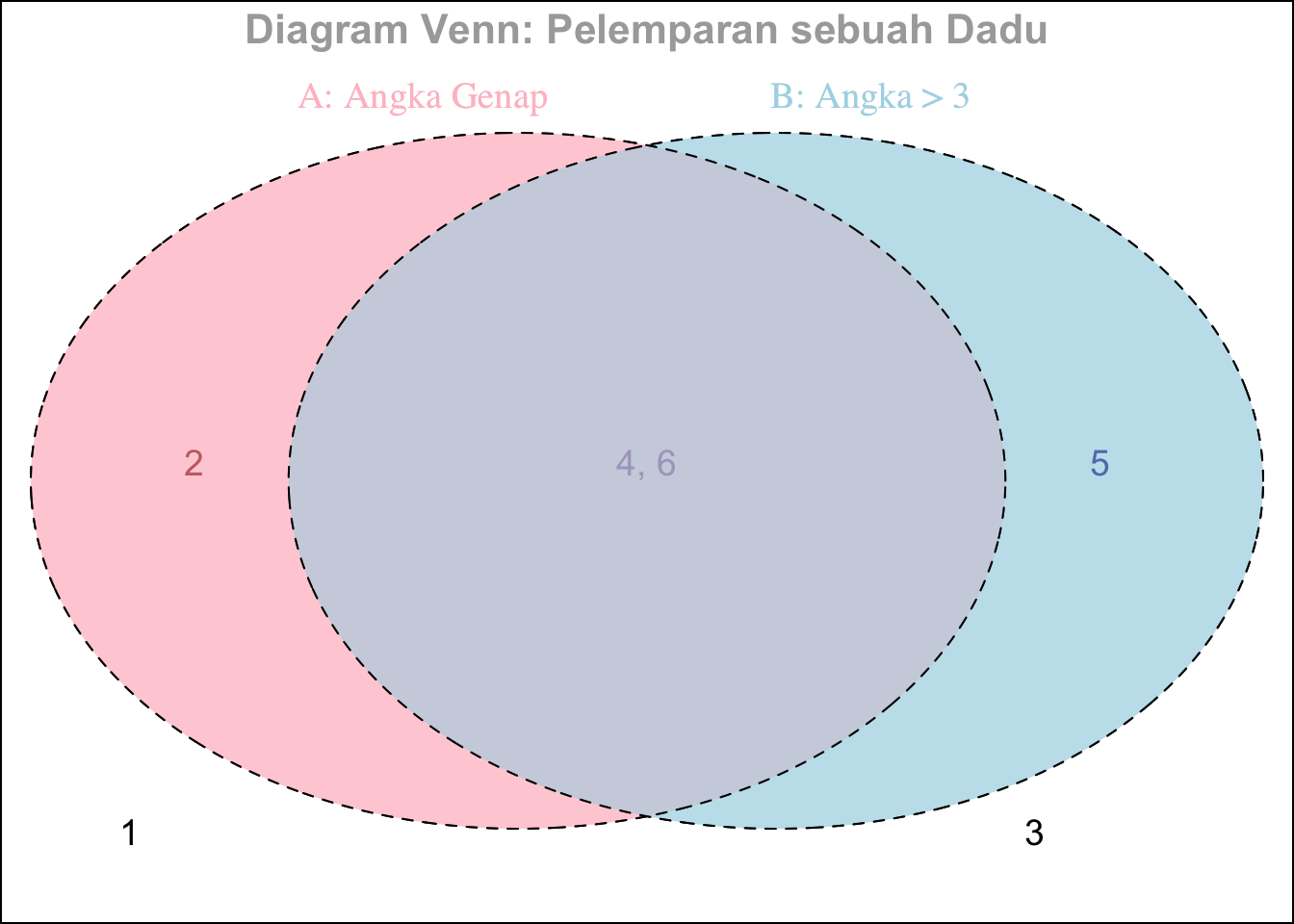
Sehingga diperoleh:

7.4.1 $P(A)$

Kejadian A terdiri dari angka genap $\{2, 4, 6\}$. Peluangnya adalah:

$$P(A) = \frac{\text{Jumlah elemen di A}}{\text{Jumlah total elemen}} = \frac{3}{6} = 0.5$$

7.4.2 $P(B)$

Kejadian B terdiri dari angka lebih dari 3 $\{4, 5, 6\}$. Peluangnya adalah:

$$P(B) = \frac{\text{Jumlah elemen di B}}{\text{Jumlah total elemen}} = \frac{3}{6} = 0.5$$

7.4.3 $P(A ∩ B))$

Kejadian A dan B yang terjadi bersamaan adalah angka yang genap dan lebih dari 3, yaitu $\{4, 6\}$. Peluangnya adalah:

$$P(A \cap B) = \frac{\text{Jumlah elemen di irisan A dan B}}{\text{Jumlah total elemen}} = \frac{2}{6} = \frac{1}{3}$$

Maka, probabilitas gabungan dari A dan B adalah:

$$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

$$P(A \cup B) = 0.5 + 0.5 - \frac{1}{3} = 1 - \frac{1}{3} = \frac{2}{3} \approx 0.6667$$

7.5 Probabilitas Bersyarat

Probabilitas bersyarat mengukur peluang kejadian $A$ terjadi, dengan syarat bahwa kejadian $B$ sudah terjadi. Probabilitas bersyarat ditulis sebagai $P(A \mid B)$ dan dihitung menggunakan rumus berikut:

$$P(A \mid B) = \frac{P(A \cap B)}{P(B)}$$

Di sini:

• $P(A \mid B)$ adalah probabilitas kejadian $A$ terjadi, dengan syarat kejadian $B$ telah terjadi.
• $P(A \cap B)$ adalah probabilitas kejadian $A$ dan $B$ terjadi bersamaan (irisan).
• $P(B)$ adalah probabilitas kejadian $B$.

Misalkan kita melakukan pelemparan dua buah dadu, dan kita memiliki dua kejadian:

• Kejadian $A$: Muncul angka genap pada pelemparan dadu pertama.
• Kejadian $B$: Muncul angka lebih dari 3 pada pelemparan dadu kedua.

Kita ingin menghitung probabilitas bersyarat $P(A \mid B)$, yaitu peluang bahwa angka yang muncul pada pelemparan dadu pertama adalah genap, dengan syarat bahwa angka pada pelemparan dadu kedua lebih besar dari 3.

Langkah-langkah untuk menghitung probabilitas bersyarat:

7.5.1 $P(A \cap B)$

Kejadian $A \cap B$ adalah kejadian di mana dadu pertama menunjukkan angka genap dan dadu kedua menunjukkan angka lebih dari 3. Angka yang memenuhi kondisi ini adalah pasangan-pasangan berikut:

• (2, 4), (2, 5), (2, 6)
• (4, 4), (4, 5), (4, 6)
• (6, 4), (6, 5), (6, 6)

Total ada 9 pasangan yang memenuhi kondisi ini. Jadi, $P(A \cap B)$ adalah:

$$P(A \cap B) = \frac{9}{36} = \frac{1}{4}$$

7.5.2 $P(B)$

Kejadian $B$ adalah angka lebih dari 3 pada dadu kedua, yang terdiri dari $\{4, 5, 6\}$. Jadi, terdapat 3 kemungkinan pada pelemparan dadu kedua, dan total kemungkinan pada pelemparan dua dadu adalah 36. Maka, $P(B)$ adalah:

$$P(B) = \frac{3 \times 6}{36} = \frac{18}{36} = \frac{1}{2}$$

7.5.3 $P(A \mid B)$

Menggunakan rumus probabilitas bersyarat:

$$P(A \mid B) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{1}{4}}{\frac{1}{2}} = \frac{1}{2}$$

Probabilitas bersyarat $P(A \mid B)$ adalah $\frac{1}{2}$, atau 50%. Artinya, jika diketahui bahwa angka pada dadu kedua lebih dari 3, maka peluang angka genap muncul pada dadu pertama adalah 50%.

7.6 Probabilitas dalam Sains Data

7.6.1 Metode Pengambilan Sampel

Pada analisis data, penting untuk menentukan ukuran sampel yang diperlukan agar estimasi dari populasi memiliki tingkat keakuratan yang diinginkan. Ukuran sampel dapat dihitung menggunakan probabilitas, tingkat kepercayaan, dan margin of error.

Rumus yang digunakan untuk menghitung ukuran sampel pada populasi besar atau tak terbatas adalah:

$$n = \frac{Z^2 \times p \times (1 - p)}{E^2}$$

Dimana:

• $n$ = jumlah sampel yang diperlukan
• $Z$ = nilai Z pada tingkat kepercayaan yang diinginkan (misalnya, untuk tingkat kepercayaan 95%, $Z = 1.96$)
• $p$ = proporsi yang diharapkan (misalnya, $p = 0.5$ jika kita tidak tahu proporsi pasti)
• $E$ = margin of error yang dapat diterima (misalnya, $E = 0.05$)

Jika ukuran populasi terbatas, rumus dapat disesuaikan dengan faktor koreksi:

$$n_{\text{adjusted}} = \frac{n}{1 + \frac{(n - 1)}{N}}$$

Dimana:

• $N$ = ukuran populasi

Misalkan Anda ingin melakukan survei pada populasi besar dengan tingkat kepercayaan 95% dan margin of error 5%. Anda memperkirakan proporsi dalam populasi adalah 50% (misalnya, 50% dari populasi menggunakan produk tertentu).

Untuk kasus ini, kita akan menghitung ukuran sampel yang diperlukan dengan menggunakan R untuk menghitung ukuran sampel. Berikut adalah kode R untuk menghitung ukuran sampel berdasarkan informasi di atas:

# Fungsi untuk menghitung ukuran sampel
sample_size <- function(Z, p, E) {
  n <- (Z^2 * p * (1 - p)) / E^2
  return(n)
}

# Parameter
Z <- 1.96    # Z untuk tingkat kepercayaan 95%
p <- 0.5     # Estimasi proporsi
E <- 0.05    # Margin of error 5%

# Hitung ukuran sampel
n <- sample_size(Z, p, E)
cat("Ukuran sampel yang diperlukan: ", ceiling(n), "\n")

## Ukuran sampel yang diperlukan:  385

Dari perhitungan di atas, ukuran sampel yang diperlukan adalah sekitar 384. Ini berarti Anda perlu mengambil sampel sebanyak 384 untuk mendapatkan estimasi dengan margin of error 5% dan tingkat kepercayaan 95%.

7.7 Studi Kasus 1

Penerapan Probabilitas dalam Prediksi Kualitas Produk:

Sebuah perusahaan manufaktur memproduksi barang elektronik dan ingin memprediksi apakah suatu produk akan cacat atau tidak. Data historis menunjukkan bahwa 5% dari produk yang diproduksi adalah cacat. Perusahaan menggunakan data tentang jenis komponen dan proses produksi untuk memprediksi cacat produk menggunakan teknik probabilitas.

7.7.1 Fitur Data

• Komponen (C): Apakah komponen elektronik yang digunakan adalah berkualitas tinggi atau rendah.
• Proses Produksi (P): Apakah proses produksi dilakukan di bawah standar atau sesuai standar.
• Cacat (D): Status cacat produk (ya/tidak).

7.7.2 Data Historis (Contoh)

• Probabilitas produk cacat ($P(D = \text{Yes})$) = 5%
• Probabilitas produk tidak cacat ($P(D = \text{No})$) = 95%
• Probabilitas menggunakan komponen berkualitas rendah ($P(C = \text{Low})$) = 30%
• Probabilitas menggunakan komponen berkualitas tinggi ($P(C = \text{High})$) = 70%
• Probabilitas proses produksi di bawah standar ($P(P = \text{Below})$) = 40%
• Probabilitas proses produksi sesuai standar ($P(P = \text{Standard})$) = 60%

Bagaimana probabilitas bahwa suatu produk akan cacat ($D = \text{Yes}$), jika diketahui komponen yang digunakan berkualitas rendah dan proses produksi di bawah standar?

Gunakan Teorema Bayes untuk menghitung probabilitas bersyarat ini:

$$P(D = \text{Yes} \mid C = \text{Low}, P = \text{Below}) = \frac{P(C = \text{Low}, P = \text{Below} \mid D = \text{Yes}) \cdot P(D = \text{Yes})}{P(C = \text{Low}, P = \text{Below})}$$

7.8 Studi Kasus 2

Penerapan Probabilitas dalam Deteksi Penipuan Transaksi:

Sebuah perusahaan e-commerce ingin mendeteksi transaksi yang berpotensi penipuan. Berdasarkan data historis, 1% dari transaksi yang dilakukan adalah penipuan. Perusahaan ingin menggunakan fitur-fitur tertentu seperti lokasi transaksi, jumlah pembelian, dan metode pembayaran untuk memprediksi apakah suatu transaksi adalah penipuan atau tidak.

7.8.1 Fitur Data

• Lokasi (L): Negara atau kota tempat transaksi dilakukan.
• Jumlah Pembelian (A): Jumlah uang yang dibelanjakan.
• Metode Pembayaran (M): Metode pembayaran yang digunakan (kartu kredit, dompet digital, dll).
• Penipuan (F): Status transaksi apakah penipuan atau tidak.

7.8.2 Data Historis (Contoh)

• Probabilitas transaksi adalah penipuan ($P(F = \text{Fraud})$) = 1%
• Probabilitas transaksi bukan penipuan ($P(F = \text{Not Fraud})$) = 99%
• Probabilitas lokasi tertentu adalah di luar negeri ($P(L = \text{Foreign})$) = 20%
• Probabilitas jumlah pembelian lebih dari $500 ($P(A = )$) = 10%
• Probabilitas menggunakan kartu kredit sebagai metode pembayaran ($P(M = \text{Credit Card})$) = 50%

Bagaimana probabilitas bahwa suatu transaksi adalah penipuan ($F = \text{Fraud}$), jika diketahui transaksi dilakukan dari lokasi luar negeri, jumlah pembelian lebih dari $500, dan metode pembayaran menggunakan kartu kredit?

Gunakan Teorema Bayes untuk menghitung probabilitas bersyarat ini:

$$P(F = \text{Fraud} \mid L = \text{Foreign}, A = \text{High}, M = \text{Credit Card}) = \frac{P(L = \text{Foreign}, A = \text{High}, M = \text{Credit Card} \mid F = \text{Fraud}) \cdot P(F = \text{Fraud})}{P(L = \text{Foreign}, A = \text{High}, M = \text{Credit Card})}$$