Chapter 5 Statistical Models

suppressPackageStartupMessages({
  library(tidyverse, quietly = TRUE)   # loading ggplot2 and dplyr
})
options(tibble.width = Inf)   # Print all the columns of a tibble (data.frame)

As always, there is a Video Lecture that accompanies this chapter.

While R is a full programming language, it was first developed by statisticians for statisticians. There are several functions to do common statistical tests but because those functions were developed early in R’s history, there is some inconsistency in how those functions work. There have been some attempts to standardize modeling object interfaces, but there were always be a little weirdness.

5.1 Formula Notation

Most statistical modeling functions rely on a formula based interface. The primary purpose is to provide a consistent way to designate which columns in a data frame are the response variable and which are the explanatory variables. In particular the notation is

\[\underbrace{y}_{\textrm{LHS response}} \;\;\; \underbrace{\sim}_{\textrm{is a function of}} \;\;\; \underbrace{x}_{\textrm{RHS explanatory}}\]

Mathematicians often refer to these terms as the Left Hand Side (LHS) and Right Hand Side (RHS). The LHS is always the response and the RHS contains the explanatory variables.

In R, the LHS is usually just a single variable in the data. However the RHS can contain multiple variables and in complicated relationships.

Right Hand Side Terms	Meaning
`x1 + x2`	Both `x1` and `x2` are additive explanatory variables. In this format, we are adding only the main effects of the `x1` and `x2` variables.
`x1:x2`	This is the interaction term between `x1` and `x2`
`x1 * x2`	Whenever we add an interaction term to a model, we want to also have the main effects. So this is a short cut for adding the main effect of `x1` and `x2` and also the interaction term `x1:x2`.
`(x1 + x2 + x3)^2`	This is the main effects of `x1`, `x2`, and `x3` and also all of the second order interactions.
`poly(x, degree=2)`	This fits the degree 2 polynomial. When fit like this, R produces an orthogonal basis for the polynomial, which is more computationally stable, but won’t be appropiate for interpreting the polynomial coefficients.
`poly(x, degree=2, raw=TRUE)`	This fits the degree 2 polynomial using $\beta_0 + \beta_1 x + \beta_2 x^2$ and the polynomial polynomial coefficients are suitable for interpretation.
`I( x^2 )`	Ignore the usual rules for interpreting formulas and do the mathematical calculation. This is not necessary for things like `sqrt(x)` or `log(x)` but required if there is a conflict between mathematics and the formula interpretation.

5.2 Basic Models

The most common statistical models are generally referred to as linear models and the R function for creating a linear model is lm(). This section will introduce how to fit the model to data in a data frame as well as how to fit very specific t-test models.

5.2.1 t-tests

There are several variants on t-tests depending on the question of interest, but they all require a continuous response and a categorical explanatory variable with two levels. If there is an obvious pairing between an observation in the first level of the explanatory variable with an observation in the second level, then it is a paired t-test, otherwise it is a two-sample t-test.

5.2.1.1 Two Sample t-tests

First we’ll import data from the Lock5Data package that gives SAT scores and gender from 343 students in an introductory statistics class. We’ll also recode the GenderCode column to be more descriptive than 0 or 1. We’ll do a t-test to examine if there is evidence that males and females have a different SAT score at the college where these data were collected.

data('GPAGender', package='Lock5Data')
GPAGender <- GPAGender %>%
  mutate( Gender = ifelse(GenderCode == 1, 'Male', 'Female'))
ggplot(GPAGender, aes(x=Gender, y=SAT)) +
  geom_boxplot()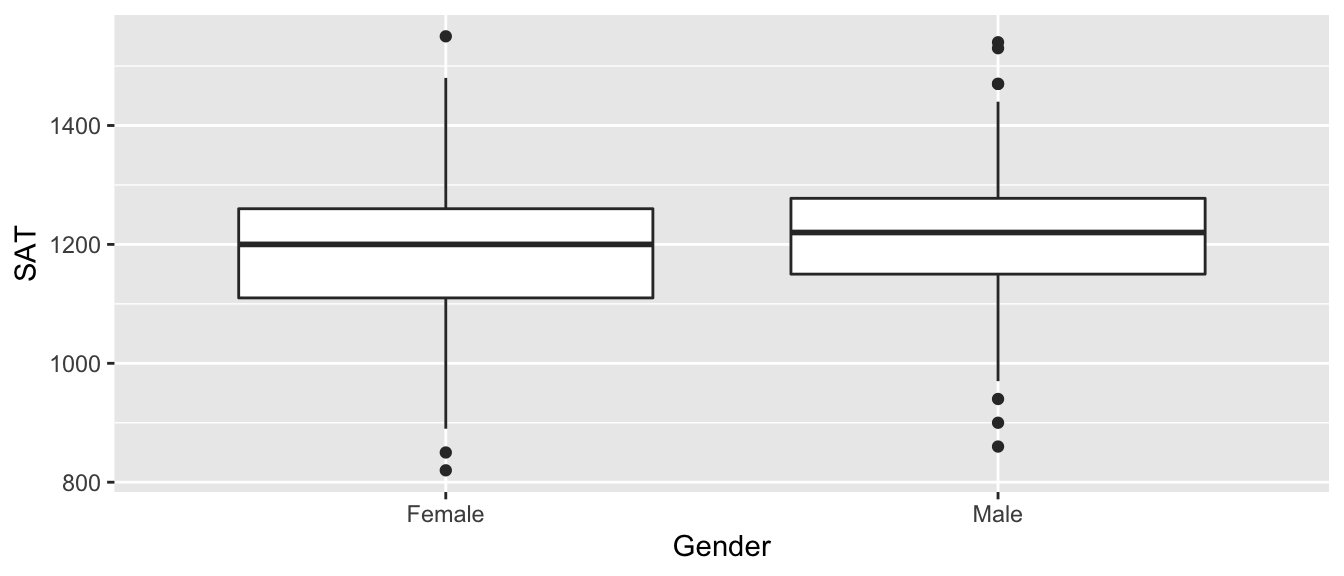

We’ll use the function t.test() using the formula interface for specifying the response and the explanatory variables. The usual practice should be to save the output of the t.test function call (typically as an object named model or model_1 or similar). Once the model has been fit, all of the important quantities have been calculated and saved and we just need to ask for them. Unfortunately, the base functions in R don’t make this particularly easy, but the tidymodels group of packages for building statistical models allows us to wrap all of the important information into a data frame with one row. In this case we will use the broom::tidy() function to extract all the important model results information.

model <- t.test(SAT ~ Gender, data=GPAGender)

print(model) # print the summary information to the screen

## 
##  Welch Two Sample t-test
## 
## data:  SAT by Gender
## t = -1.4135, df = 323.26, p-value = 0.1585
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -44.382840   7.270083
## sample estimates:
## mean in group Female   mean in group Male 
##             1195.702             1214.258

broom::tidy(model) # all that information as a data frame

## # A tibble: 1 x 10
##   estimate estimate1 estimate2 statistic p.value parameter conf.low conf.high
##      <dbl>     <dbl>     <dbl>     <dbl>   <dbl>     <dbl>    <dbl>     <dbl>
## 1    -18.6     1196.     1214.     -1.41   0.158      323.    -44.4      7.27
##   method                  alternative
##   <chr>                   <chr>      
## 1 Welch Two Sample t-test two.sided

In the t.test function, the default behavior is to perform a test with a two-sided alternative and to calculate a 95% confidence interval. Those can be adjusted using the alternative and conf.level arguments. See the help documentation for t.test() function to see how to adjust those.

The t.test function can also be used without using a formula by inputting a vector of response variables for the first group and a vector of response variables for the second. The following results in the same model as the formula based interface.

male_SATs   <- GPAGender %>% filter( Gender ==   'Male' ) %>% pull(SAT)
female_SATs <- GPAGender %>% filter( Gender == 'Female' ) %>% pull(SAT)

model <- t.test( male_SATs, female_SATs )
broom::tidy(model) # all that information as a data frame

## # A tibble: 1 x 10
##   estimate estimate1 estimate2 statistic p.value parameter conf.low conf.high
##      <dbl>     <dbl>     <dbl>     <dbl>   <dbl>     <dbl>    <dbl>     <dbl>
## 1     18.6     1214.     1196.      1.41   0.158      323.    -7.27      44.4
##   method                  alternative
##   <chr>                   <chr>      
## 1 Welch Two Sample t-test two.sided

5.2.1.2 Paired t-tests

In a paired t-test, there is some mechanism for pairing observations in the two categories. For example, perhaps we observe the maximum weight lifted by a strongman competitor while wearing a weight belt vs not wearing the belt. Then we look at the difference between the weights lifted for each athlete. In the example we’ll look at here, we have the ages of 100 randomly selected married heterosexual couples from St. Lawerence County, NY. For any given man in the study, the obvious woman to compare his age to is his wife’s. So a paired test makes sense to perform.

data('MarriageAges', package='Lock5Data')
str(MarriageAges)

## 'data.frame':    105 obs. of  2 variables:
##  $ Husband: int  53 38 46 30 31 26 29 48 65 29 ...
##  $ Wife   : int  50 34 44 36 23 31 25 51 46 26 ...

ggplot(MarriageAges, aes(x=Husband, y=Wife)) +
  geom_point() + labs(x="Husband's Age", y="Wife's Age")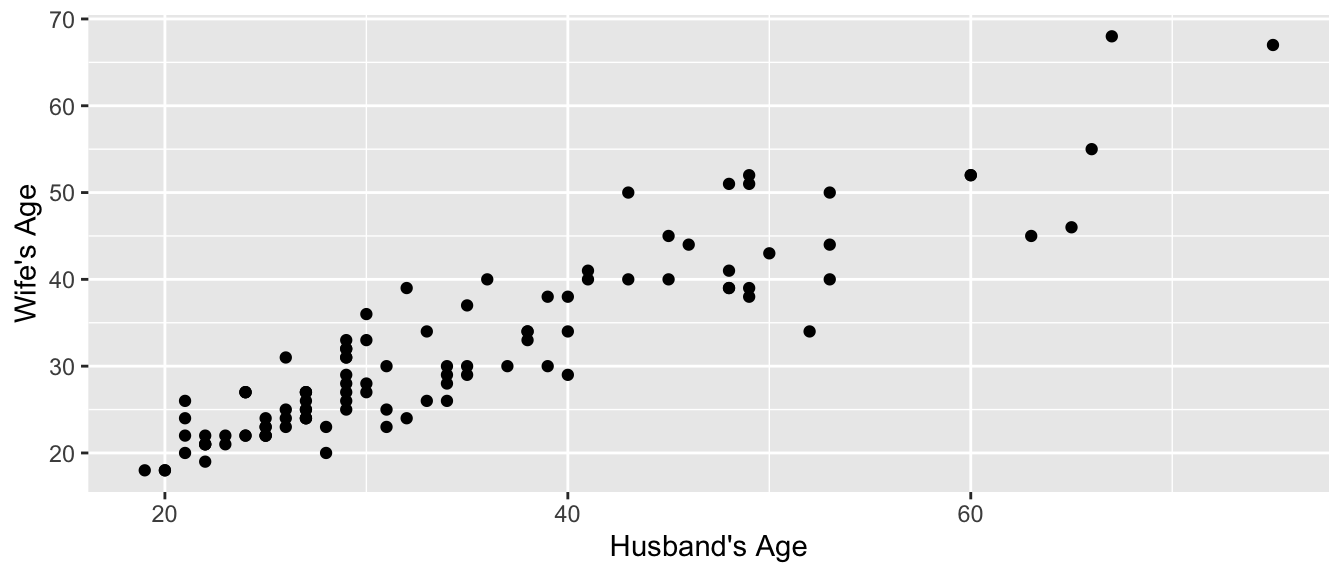

To do a paired t-test, all we need to do is calculate the difference in age for each couple and pass that into the t.test() function.

MarriageAges <- MarriageAges %>%
  mutate( Age_Diff = Husband - Wife)

t.test( MarriageAges$Age_Diff)

## 
##  One Sample t-test
## 
## data:  MarriageAges$Age_Diff
## t = 5.8025, df = 104, p-value = 7.121e-08
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  1.861895 3.795248
## sample estimates:
## mean of x 
##  2.828571

Alternatively, we could pass the vector of Husband ages and the vector of Wife ages into the t.test() function and tell it that the data is paired so that the first husband is paired with the first wife.

t.test( MarriageAges$Husband, MarriageAges$Wife, paired=TRUE )

## 
##  Paired t-test
## 
## data:  MarriageAges$Husband and MarriageAges$Wife
## t = 5.8025, df = 104, p-value = 7.121e-08
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  1.861895 3.795248
## sample estimates:
## mean of the differences 
##                2.828571

Either way that the function is called, the broom::tidy() function could convert the printed output into a nice data frame which can then be used in further analysis.

5.2.2 lm objects

The general linear model function lm is more widely used than t.test because lm can be made to perform a t-test and the general linear model allows for fitting more than one explanatory variable and those variables could be either categorical or continuous.

The general work-flow will be to:

Visualize the data
Call lm() using a formula to specify the model to fit.
Save the results of the lm() call to some object (usually I name it model)
Use accessor functions to ask for pertinent quantities that have already been calculated.
Store prediction values and model confidence intervals for each data point in the original data frame.
Graph the original data along with prediction values and model confidence intervals.

To explore this topic we’ll use the iris data set to fit a regression model to predict petal length using sepal length.

ggplot(iris, aes(x=Sepal.Length, y=Petal.Length, color=Species)) +
  geom_point()

Now suppose we want to fit a regression model to these data and allow each species to have its own slope. We would fit the interaction model

model <- lm( Petal.Length ~ Sepal.Length * Species, data = iris )

5.3 Accessor functions

Once a model has been fit, we want to obtain a variety of information from the model object. The way that we get most all of this information using base R commands is to call the summary() function which returns a list and then grab whatever we want out of that. Typically for a report, we could just print out all of the summary information and let the reader pick out the information.

summary(model)

## 
## Call:
## lm(formula = Petal.Length ~ Sepal.Length * Species, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.68611 -0.13442 -0.00856  0.15966  0.79607 
## 
## Coefficients:
##                                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                      0.8031     0.5310   1.512    0.133    
## Sepal.Length                     0.1316     0.1058   1.244    0.216    
## Speciesversicolor               -0.6179     0.6837  -0.904    0.368    
## Speciesvirginica                -0.1926     0.6578  -0.293    0.770    
## Sepal.Length:Speciesversicolor   0.5548     0.1281   4.330 2.78e-05 ***
## Sepal.Length:Speciesvirginica    0.6184     0.1210   5.111 1.00e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2611 on 144 degrees of freedom
## Multiple R-squared:  0.9789, Adjusted R-squared:  0.9781 
## F-statistic:  1333 on 5 and 144 DF,  p-value: < 2.2e-16

But if we want to make a nice graph that includes the model’s $R^2$ value on it, we need to code some way of grabbing particular bits of information from the model fit and wrestling into a format that we can easily manipulate it.

Goal	Base R command	`tidymodels` version
Summary table of Coefficients	`summary(model)$coef`	`broom::tidy(model)`
Parameter Confidence Intervals	`confint(model)`	`broom::tidy(model, conf.int=TRUE)`
Rsq and Adj-Rsq	`summary(model)$r.squared`	`broom::glance(model)`
Model predictions	`predict(model)`	`broom::augment(model, data)`
Model residuals	`resid(model)`	`broom::augment(model, data)`
Model predictions w/ CI	`predict(model, interval='confidence')`
Model predictions w/ PI	`predict(model, interval='prediction')`
ANOVA table of model fit	`anova(model)`

The package broom has three ways to interact with a model.

The tidy command gives a nice table of the model coefficients.
The glance function gives information about how well the model fits the data overall.
The augment function adds the fitted values, residuals, and other diagnostic information to the original data frame used to generate the model. Unfortunately it does not have a way of adding the lower and upper confidence intervals for the predicted values.

Most of the time, I use the base R commands for accessing information from a model and only resort to the broom commands when I need to access very specific quantities.

head(iris)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1          5.1         3.5          1.4         0.2  setosa
## 2          4.9         3.0          1.4         0.2  setosa
## 3          4.7         3.2          1.3         0.2  setosa
## 4          4.6         3.1          1.5         0.2  setosa
## 5          5.0         3.6          1.4         0.2  setosa
## 6          5.4         3.9          1.7         0.4  setosa

predict(model, interval='confidence')

##          fit      lwr      upr
## 1   1.474373 1.398783 1.549964
## 2   1.448047 1.371765 1.524329
## 3   1.421721 1.324643 1.518798
## 4   1.408558 1.296579 1.520536
## 5   1.461210 1.388211 1.534210
## 6   1.513863 1.403776 1.623950
## 7   1.408558 1.296579 1.520536
## 8   1.461210 1.388211 1.534210
## 9   1.382231 1.235963 1.528500
## 10  1.448047 1.371765 1.524329
## 11  1.513863 1.403776 1.623950
## 12  1.434884 1.350125 1.519642
## 13  1.434884 1.350125 1.519642
## 14  1.369068 1.204342 1.533794
## 15  1.566516 1.385105 1.747926
## 16  1.553352 1.390873 1.715832
## 17  1.513863 1.403776 1.623950
## 18  1.474373 1.398783 1.549964
## 19  1.553352 1.390873 1.715832
## 20  1.474373 1.398783 1.549964
## 21  1.513863 1.403776 1.623950
## 22  1.474373 1.398783 1.549964
## 23  1.408558 1.296579 1.520536
## 24  1.474373 1.398783 1.549964
## 25  1.434884 1.350125 1.519642
## 26  1.461210 1.388211 1.534210
## 27  1.461210 1.388211 1.534210
## 28  1.487537 1.404026 1.571047
## 29  1.487537 1.404026 1.571047
## 30  1.421721 1.324643 1.518798
## 31  1.434884 1.350125 1.519642
## 32  1.513863 1.403776 1.623950
## 33  1.487537 1.404026 1.571047
## 34  1.527026 1.400518 1.653534
## 35  1.448047 1.371765 1.524329
## 36  1.461210 1.388211 1.534210
## 37  1.527026 1.400518 1.653534
## 38  1.448047 1.371765 1.524329
## 39  1.382231 1.235963 1.528500
## 40  1.474373 1.398783 1.549964
## 41  1.461210 1.388211 1.534210
## 42  1.395394 1.266828 1.523961
## 43  1.382231 1.235963 1.528500
## 44  1.461210 1.388211 1.534210
## 45  1.474373 1.398783 1.549964
## 46  1.434884 1.350125 1.519642
## 47  1.474373 1.398783 1.549964
## 48  1.408558 1.296579 1.520536
## 49  1.500700 1.405258 1.596141
## 50  1.461210 1.388211 1.534210
## 51  4.990404 4.821805 5.159003
## 52  4.578522 4.479932 4.677112
## 53  4.921757 4.765911 5.077603
## 54  3.960699 3.864752 4.056647
## 55  4.647169 4.538461 4.755877
## 56  4.097993 4.017596 4.178390
## 57  4.509875 4.420261 4.599489
## 58  3.548817 3.383814 3.713820
## 59  4.715816 4.596137 4.835495
## 60  3.754758 3.626775 3.882741
## 61  3.617464 3.465141 3.769788
## 62  4.235287 4.162117 4.308457
## 63  4.303934 4.230375 4.377493
## 64  4.372581 4.295925 4.449237
## 65  4.029346 3.941992 4.116701
## 66  4.784463 4.653175 4.915751
## 67  4.029346 3.941992 4.116701
## 68  4.166640 4.091110 4.242170
## 69  4.441228 4.359073 4.523383
## 70  4.029346 3.941992 4.116701
## 71  4.235287 4.162117 4.308457
## 72  4.372581 4.295925 4.449237
## 73  4.509875 4.420261 4.599489
## 74  4.372581 4.295925 4.449237
## 75  4.578522 4.479932 4.677112
## 76  4.715816 4.596137 4.835495
## 77  4.853110 4.709728 4.996491
## 78  4.784463 4.653175 4.915751
## 79  4.303934 4.230375 4.377493
## 80  4.097993 4.017596 4.178390
## 81  3.960699 3.864752 4.056647
## 82  3.960699 3.864752 4.056647
## 83  4.166640 4.091110 4.242170
## 84  4.303934 4.230375 4.377493
## 85  3.892052 3.786274 3.997831
## 86  4.303934 4.230375 4.377493
## 87  4.784463 4.653175 4.915751
## 88  4.509875 4.420261 4.599489
## 89  4.029346 3.941992 4.116701
## 90  3.960699 3.864752 4.056647
## 91  3.960699 3.864752 4.056647
## 92  4.372581 4.295925 4.449237
## 93  4.166640 4.091110 4.242170
## 94  3.617464 3.465141 3.769788
## 95  4.029346 3.941992 4.116701
## 96  4.097993 4.017596 4.178390
## 97  4.097993 4.017596 4.178390
## 98  4.441228 4.359073 4.523383
## 99  3.686111 3.546158 3.826065
## 100 4.097993 4.017596 4.178390
## 101 5.335977 5.255712 5.416242
## 102 4.960936 4.843994 5.077878
## 103 5.936041 5.841958 6.030125
## 104 5.335977 5.255712 5.416242
## 105 5.485993 5.412294 5.559691
## 106 6.311082 6.172893 6.449271
## 107 4.285864 4.076975 4.494753
## 108 6.086057 5.975863 6.196252
## 109 5.636009 5.561874 5.710144
## 110 6.011049 5.909252 6.112847
## 111 5.485993 5.412294 5.559691
## 112 5.410985 5.334811 5.487159
## 113 5.711017 5.634000 5.788034
## 114 4.885928 4.759719 5.012137
## 115 4.960936 4.843994 5.077878
## 116 5.410985 5.334811 5.487159
## 117 5.485993 5.412294 5.559691
## 118 6.386090 6.237929 6.534251
## 119 6.386090 6.237929 6.534251
## 120 5.110953 5.011075 5.210830
## 121 5.786025 5.704563 5.867487
## 122 4.810920 4.675086 4.946754
## 123 6.386090 6.237929 6.534251
## 124 5.335977 5.255712 5.416242
## 125 5.636009 5.561874 5.710144
## 126 6.011049 5.909252 6.112847
## 127 5.260969 5.175229 5.346708
## 128 5.185961 5.093608 5.278313
## 129 5.410985 5.334811 5.487159
## 130 6.011049 5.909252 6.112847
## 131 6.161066 6.041937 6.280195
## 132 6.536106 6.367377 6.704835
## 133 5.410985 5.334811 5.487159
## 134 5.335977 5.255712 5.416242
## 135 5.185961 5.093608 5.278313
## 136 6.386090 6.237929 6.534251
## 137 5.335977 5.255712 5.416242
## 138 5.410985 5.334811 5.487159
## 139 5.110953 5.011075 5.210830
## 140 5.786025 5.704563 5.867487
## 141 5.636009 5.561874 5.710144
## 142 5.786025 5.704563 5.867487
## 143 4.960936 4.843994 5.077878
## 144 5.711017 5.634000 5.788034
## 145 5.636009 5.561874 5.710144
## 146 5.636009 5.561874 5.710144
## 147 5.335977 5.255712 5.416242
## 148 5.485993 5.412294 5.559691
## 149 5.260969 5.175229 5.346708
## 150 5.035944 4.927819 5.144070

# Remove any previous model prediction values that I've added,
# and then add the model predictions 
iris <- iris %>%
  dplyr::select( -matches('fit'), -matches('lwr'), -matches('upr') ) %>%
  cbind( predict(model, newdata=., interval='confidence') )       

head(iris, n=3)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width Species      fit      lwr
## 1          5.1         3.5          1.4         0.2  setosa 1.474373 1.398783
## 2          4.9         3.0          1.4         0.2  setosa 1.448047 1.371765
## 3          4.7         3.2          1.3         0.2  setosa 1.421721 1.324643
##        upr
## 1 1.549964
## 2 1.524329
## 3 1.518798

Now that the fitted values that define the regression lines and the associated confidence interval band information have been added to my iris data set, we can now plot the raw data and the regression model predictions.

ggplot(iris, aes(x=Sepal.Length, color=Species)) +
  geom_point( aes(y=Petal.Length) ) +
  geom_line( aes(y=fit) ) +
  geom_ribbon( aes( ymin=lwr, ymax=upr, fill=Species), alpha=.3 )   # alpha is the ribbon transparency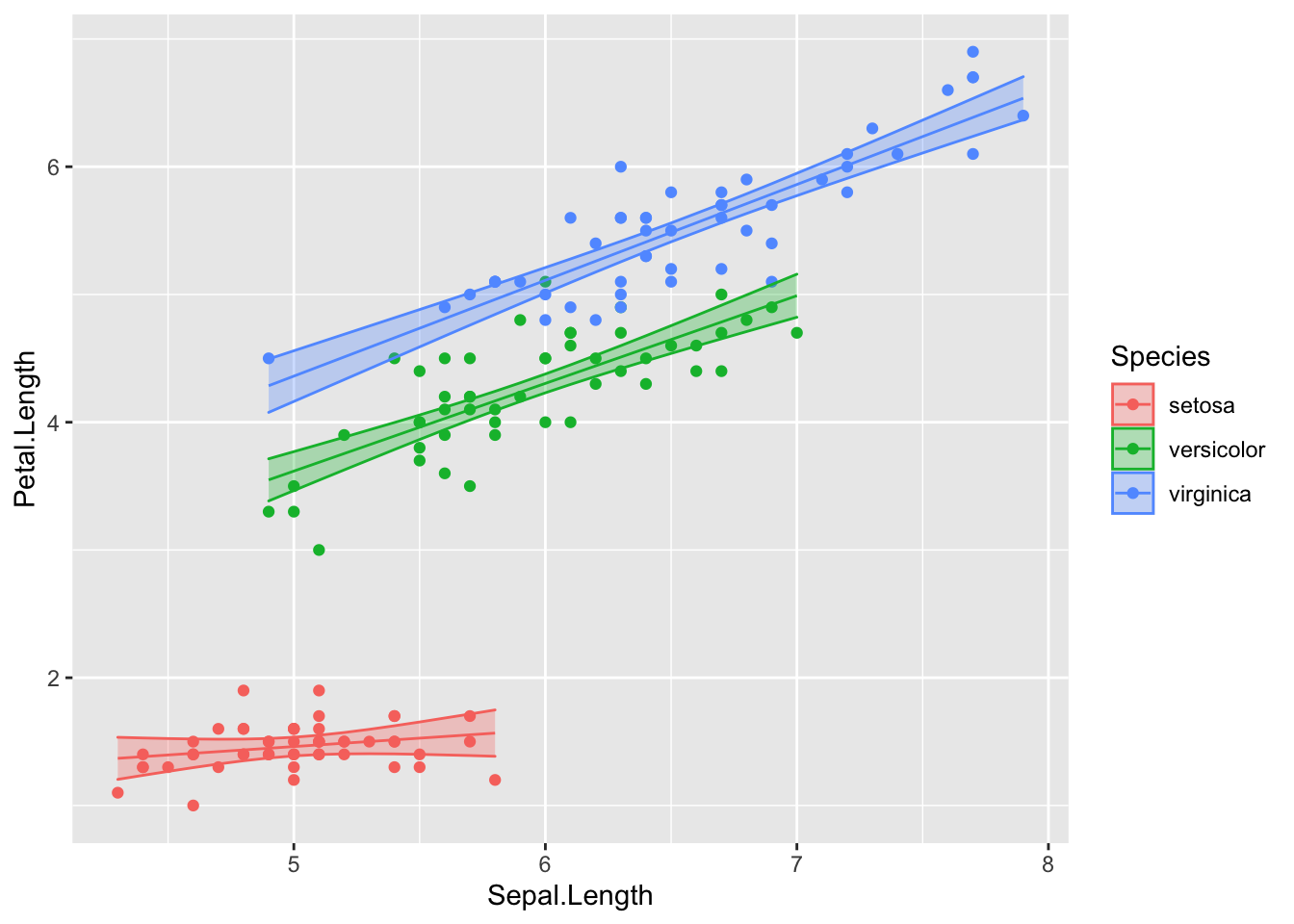

Now to add the R-squared value to the graph, we need to add a simple text layer. To do that, I’ll make a data frame that has the information, and then add the x and y coordinates for where it should go.

Rsq_string <- 
  broom::glance(model) %>%
  select(r.squared) %>%
  mutate(r.squared = round(r.squared, digits=3)) %>%   # only 3 digits of precision
  mutate(r.squared = paste('Rsq =', r.squared)) %>%    # append some text before
  pull(r.squared)           

ggplot(iris, aes(x=Sepal.Length, y=Petal.Length, color=Species)) +
  geom_point(  ) +
  geom_line( aes(y=fit)  ) +
  geom_ribbon( aes( ymin=lwr, ymax=upr, fill=Species), alpha=.3 ) +   # alpha is the ribbon transparency
  annotate('label', label=Rsq_string, x=7, y=2, size=7)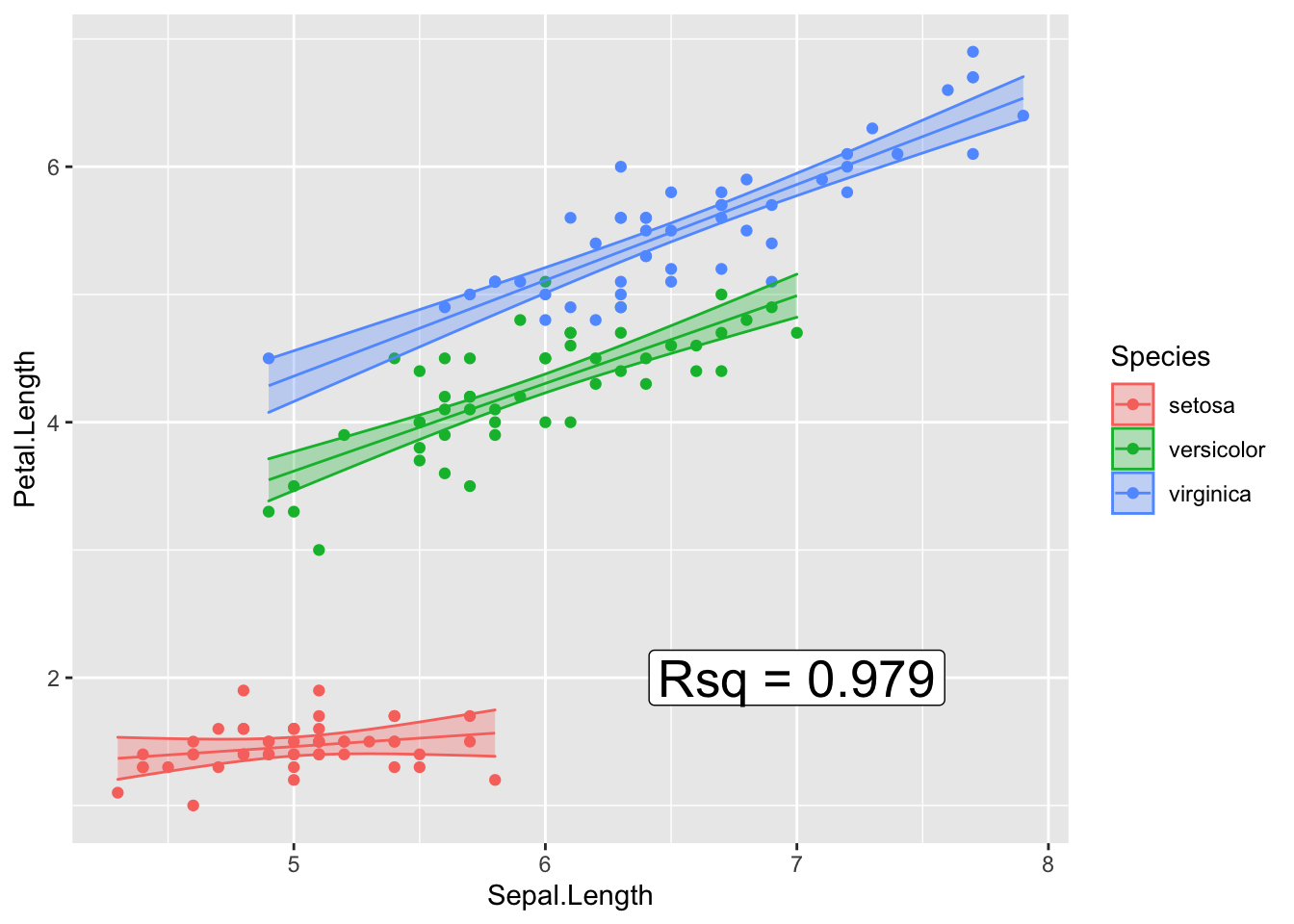

5.4 Exercises

Using the trees data frame that comes pre-installed in R, fit the regression model that uses the tree Height to explain the Volume of wood harvested from the tree.
1. Graph the data
2. Fit a lm model using the command model <- lm(Volume ~ Height, data=trees).
3. Print out the table of coefficients with estimate names, estimated value, standard error, and upper and lower 95% confidence intervals.
4. Add the model fitted values to the trees data frame along with the regression model confidence intervals.
5. Graph the data and fitted regression line and uncertainty ribbon.
6. Add the R-squared value as an annotation to the graph.
The data set phbirths from the faraway package contains information on birth weight, gestational length, and smoking status of mother. We’ll fit a quadratic model to predict infant birth weight using the gestational time.
1. Create two scatter plots of gestational length and birth weight, one for each smoking status.
2. Remove all the observations that are premature (less than 36 weeks). For the remainder of the problem, only use these full-term babies.
3. Fit the quadratic model
```
model <- lm(grams ~ poly(gestate,2) * smoke, data=phbirths)
```
4. Add the model fitted values to the phbirths data frame along with the regression model confidence intervals.
5. On your two scatter plots from part (a), add layers for the model fits and ribbon of uncertainty for the model fits.
6. Create a column for the residuals in the phbirths data set using any of the following:
```
phbirths$residuals = resid(model)
phbirths <- phbirths %>% mutate( residuals = resid(model) )
phbirths <- broom::augment(model, phbirths)
```
7. Create a histogram of the residuals.