6. nodaļa. Statistiskie rādītāji un ticamības intervāli
6.1 Statistiskie rādītāji
6.1.1 Teorētiskais pamatojums
Paraugkopas un ģenerālkopas raksturošanai un informācijas apkopošanai izmanto statistiskos rādītājus. Tos iedala vairākās grupās, no kurām svarīgākās ir vidējie rādītāji un izkliedes radītāji.
6.1.1.1 Vidējie rādītāji
Vidējie rādītāji parāda kāda ir vidējā vērtība paraugkopas datiem katrai konkrētajai pazīmei.
6.1.1.2 Vidējais aritmētiskais (\(\overline{x}\))
Visbiežāk lietotais vidējais rādītājs ir vidējais aritmētiskais, kas, atbilstoši tā nosaukumam, parāda kāda ir vidēja vērtība. Tā aprēķināšanu veic pēc formulas (\ref{eq:vvarit}):
\begin{equation} \overline{x}=\frac{\sum\limits_{i=1}^{n}x_i}{n} \label{eq:vvarit} \end{equation}kur \(x_i\) - i-tā paraugkopas vērtībā, i=1, 2, …, n, n - paraugkopas apjoms.
Attiecībā uz vidējo aritmētisko ir jāņem vērā, ka tā vērtība ir atkarīga no katras variantes datos, tāpēc vidējais aritmētiskais ir jutīgs pret ekstremāli mazām vai lielām vērtībām. Piemēram, ja datos ir viena ļoti liela vērtība, tad ir iespējama situācija, ka vidējais aritmētiskais ir mazāks tikai par šo ekstremāli lielo vērtību, bet lielāks par visām pārējām vērtībām.
6.1.1.3 Mediāna (\(M_e\))
Mediāna ir tā konkrētās paraugkopas vērtība līdz kurai atrodas 50% no visām vērtībām (ja tās sakārtotas augošā vai dilstošā secībā). Piemēram, ja paraugkopā ir nepāra skaits novērojumu, pieņemsim, pieci, tad mediāna būs trešā vērtība. Ja paraugkopā ir pāra skaits novērojumu, pieņemsim seši, tad mediāna būs vidējais aritmētiskais starp trešo un ceturto vērtību. Atšķirībā no vidējā aritmētiskā, mediāna nav jutīga pret ekstremālām vērtībām, jo tās aprēķins balstās uz vērtību izkārtojumu, nevis uz to absolūtajām vērtībām.
6.1.1.4 Kvartiles (\(Q_i\))
Kvartiles augošā/dilstošā secibā sakārtotas paraugkopas vērtības sadala četrās vienādās daļās. 0. kvartile atbilst minimālajai vērtībai, līdz 1. kvartilei atrodas 25% no visiem novērojumiem,līdz 2. kvartilei atrodas 50% novērojumu un tā ir vienāda ar mediānu. Līdz 3. kvartilei atrodas 75% no visiem novērojumiem, un 4. kvartile ir vienāda ar maksimālo vērtību.
6.1.1.5 Procentile (\(P_i\))
Procentiles augošā/dilstošā secībā sakārtotas paraugkopas vērtības sadala 100 vienādās daļās.
6.1.1.6 Izkliedes rādītāji
Vidējie rādītāji sniedz informāciju par vidējo tendenci datos, bet, lai iegūtu pilnu ainu par datiem, ir jāizmanto arī izkliedes rādītāji, kas parāda kādā veidā paraugkopas vērtības ir izkliedētas ap vidējo vērtību.
6.1.1.7 Standartnovirze (s) un dispersija (\(s^2\))
Svarīgākie izkliedes rādītāji ir dispersija un standartnovirze. Dispersiju paraugkopai aprēķina pēc formulas (\ref{eq:disneg}) un tā parāda, kāda ir vidējā kvadrātiskā novirze no vidējā aritmētiskā. Standartnovirze (\ref{eq:stand}) attiecīgi ir kvadrātsakne no dispersijas. Standartnovirzei ir tāda paša mērvienība kā paraugkopas datiem. Jo lielākas ir dispersijas un standartnovirzes vērtības, jo lielāka ir datu izkliede ap vidējo aritmētisko.
\begin{equation} s^2=\frac{\sum\limits_{i=1}^{n}(x_i-\overline{x})^2}{n-1} \label{eq:disneg} \end{equation}\begin{equation} s=\sqrt{\frac{\sum\limits_{i=1}^{n}(x_i-\overline{x})^2}{n-1}} \label{eq:stand} \end{equation}kur \(x_i\) - i-tā paraugkopas vērtībā, i=1, 2, …, n, n - paraugkopas apjoms, \(\overline{x}\) - paraugkopas vidējais aritmētiskais.
6.1.1.8 Variācijas koeficients (v)
Standartnovirze ne vienmēr ir labākais rādītājs, lai salīdzinātu vērtību izkliedi starp dažādiem rādītājiem, sevišķi, ja tiem atšķiras mērvienības. Šajā gadījumā labāks rādītājs ir variācijas koeficients (\ref{eq:varkoe}). Variācijas koeficients ir rādītājs bez mērvienības, jo to iegūst dalot standartnovirzi ar vidējo aritmētisko. Variācijas koeficientu var izteikt arī procentos, attiecīgi sareizinot tā vērtību ar 100%.
\begin{equation} v=\frac{s}{\overline{x}} \label{eq:varkoe} \end{equation}kur s - paraugkopas standartnovirze, \(\overline{x}\) - paraugkopas vidējais aritmētiskais.
6.1.2 Statistisko rādītāju aprēķināšana programmā R
Piemēram par statistisko rādītāju aprēķināšanu izmantot datu fails niedres2.txt, kas satur informāciju par niedru lapu garumu un platumu trīs parauglaukumos.
niedr<-read.table(file="niedres2.txt",header=TRUE,sep="\t",dec=".")
str(niedr)## 'data.frame': 50 obs. of 3 variables:
## $ garums : num 31.6 23.2 39.2 37.4 21.1 37 24.7 31.3 37.4 39.7 ...
## $ platums: num 2.5 2.3 2.1 5.8 2.2 4.1 3.5 4.2 2.5 2.8 ...
## $ paraug : Factor w/ 3 levels "Austr","Riet",..: 1 1 1 1 1 1 1 1 1 1 ...Pamatstatistisko rādītāju aprēķināšanai ir jau definētas funkcijas: mean() - vidējais aritmētiskais, sd() - standartnovirze, var() - dispersija, median() - mediāna. Visām šīm funkcijām kā mainīgais jānorada viena kolonna/vektors un tiks aprēķināts vēlamais rādītājs.
mean(niedr$garums)## [1] 37.594sd(niedr$garums)## [1] 10.31332var(niedr$garums)## [1] 106.3647median(niedr$garums)## [1] 38.4Veicot aprēķinus rezultātam ciparu skaits aiz komata ir atkarīgs no tā, kādi ir sesijas uzstādījumi. Ja ir nepieciešams noapaļot skaitļus, var izmantot papildus funkciju round(), kurā norāda apaļojamo mainīgo vai visu funkciju, kā arī jānorāda vēlamais ciparu skaits aiz komata. Ir jāatceras, ka noapaļot drīkst tikai gala rezultātus - ja noapaļo skaitļus, kurus vēlāk izmanto citos aprēķinos, tas samazina iegūtā rezultāta precizitāti.
round(mean(niedr$garums),2)## [1] 37.59Viena no daudzu programmas R funkciju īpatnībām ir tā, ka nav iespējams iegūt rezultātu, ja dati satur kādu iztrūkstošu vērtību. Piemēram, radam vektoru x, kas satur 20 skaitļus no normālā sadalījuma un vienu iztrūkstošu vērtību, ko R apzīmē ar NA. Ja šādam vektoram cenšas aprēķināt vidējo aritmētisko ar funkciju mean(), iegūst rezultātu NA, jo nezināmā vērtība var būt jebkas, attiecīgi arī vidējais var būt jebkas.
set.seed(1234)
x<-c(rnorm(20),NA)
mean(x)## [1] NAŠādā situācijā var norādīt, ka NA vērtības ir jāignorē. To panāk funkcijai kā papildus argumentu norādot na.rm=TRUE. Daļai funkciju šī argumenta pieraksts var būt atšķirīgs, to var precizēt funkcijas aprakstā.
mean(x,na.rm=TRUE)## [1] -0.2506641Minimālās un maksimālās vērtības aprēķināšanai var izmantot attiecīgi funkcijas min() un max(), vai arī funkciju range(), kas aprēķina uzreiz abus šos rādītājus.
min(niedr$garums)## [1] 11.9max(niedr$garums)## [1] 59range(niedr$garums)## [1] 11.9 59.0Kvartiļu aprēķināšanai izmanto funkciju quantile(), kas pārādīs uzreiz visas kvartiles tās izsakot kā procentiles.
quantile(niedr$garums)## 0% 25% 50% 75% 100%
## 11.900 31.075 38.400 45.300 59.000Ja ir nepieciešams aprēķināt procentiles, vai arī tikai kādu noteiktu kvartili, funkcijai quantile() kā papildus arguments jānorāda probs= un nepieciešamā procentile izteikta decimāldaļās.
quantile(niedr$garums,probs=c(0.025,0.975))## 2.5% 97.5%
## 18.465 55.770Ar funkciju summary() ir iespējams aprēķināt uzreiz vairākus statistiskos radītājus, kas raksturo mainīgo. Šie rādītāji ir minimālā vērtība, 1. kvartile, mediāna, vidējais aritmētiskais, 3. kvartile un maksimālā vērtība. Šai funkcijai kā mainīgo var norādīt vienu kolonnu vai vektoru.
summary(niedr$garums)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 11.90 31.08 38.40 37.59 45.30 59.00Ja funkcijā summary() kā mainīgo norāda veselu datu tabulu, tad iepriekš minētie rādītāji tiek aprēķināti katrai kolonnai, kas satur skaitlisku informāciju. Kolonnai, kas satur faktoru jeb tekstuālu informāciju, aprēķina cik bieži atkārtojas katra unikālā vērtība.
summary(niedr)## garums platums paraug
## Min. :11.90 Min. :0.400 Austr:17
## 1st Qu.:31.07 1st Qu.:2.500 Riet :17
## Median :38.40 Median :3.900 Ziem :16
## Mean :37.59 Mean :3.892
## 3rd Qu.:45.30 3rd Qu.:5.100
## Max. :59.00 Max. :7.100Funkcija tapply() ir ļoti noderīga gadījumos, ja nepieciešams aprēķināt kādu rādītāju viena vektora/kolonnas vērtībām tās sadalot pa līmeņiem, kurus nosaka otrs vektors/kolonna. Funkcijā jānorāda mainīgais, kas satur vērtības, mainīgais, kas satur dalījuma līmeņus, un funkcija, kuru izmantot aprēķinos. Ir iespējams izmantot ne tikai jau definētas funckijas, bet arī definēt jaunas funkcijas, izmantojot function() funkciju. Piemērā aprēķināta standartnovirze kolonnai garums, ka sadalīta pa parauglaukumiem.
tapply(niedr$garums,niedr$paraug,sd)## Austr Riet Ziem
## 8.869876 9.376174 11.7064016.2 Ticamības intervāli
6.2.1 Teorētiskais pamatojums
Veicot pētījumus vairumā gadījumu tiek strādāts ar paraugkopu, nevis ar visu ģenerālkopu. Attiecīgi no paraugkopas datiem iegūtais, piemēram, vidējais aritmētiskais nebūs vienāds ar ģenerālkopas vidējo aritmētisko, kaut arī daudzos gadījumos tas tā tiek pieņemts. Precīzākai ģenerālkopas vērtējamā rādītāja raksturošanai var izmantot ticamības intervālu. Ticmības intervāla interpretē tā, ka izveiddojot daudzas jaunas paraugkopas un aprēķinot tām ticamības intervālu, tiacamības līmenim atbilstošo reižu gadījumā šajā intervālā atradīsies konkrētais ģenerālkopas rādītājs, kas tiek novērtēts. Ticamības intervālu var aprēķināt ne tikai ģenerālkopu raksturojošiem rādītājiem kā vidējais aritmētiskais un standartnovirze, bet arī jebkuram citam rādītājām, piemēram, korelācijas koeficientam starp divām paraugkopām.
6.2.1.1 Vidējā aritmētiskā ticamības intervāls
Vidējā aritmētiskā ticamības intervāla aprēķināšanai ir vairākas formulas, kuras atšķiras pēc tā, vai ir zināma vai nav zināma ģenerālkopas standartnovirze. Tā kā vairumā gadījumu tā nav zināma, tad izmantota formula intervāla aprēķināšanai izmantojot tikai paraugkopas datus. Šai formulai pieņēmums ir, ka paraugkopas dati ir nākuši no ģenerālkopas, kas seko normālajam sadalījumam. Ticamības intervālam aprēķina augšējo un apakšējo robežu pēc formulas (\ref{eq:ticvid}). Stjūdenta kritērija teorētisko vērtību pie atbilstošā būtiskuma līmeņa var atrast speciālās statistiskas tabulās, vai arī aprēķināt.
\begin{equation} \overline{x}-t_{\alpha/2,\nu} \cdot s_{\overline{x}} < \mu < \overline{x}+t_{\alpha/2,\nu} \cdot s_{\overline{x}} \label{eq:ticvid} \end{equation}kur \(\overline{x}\) - vidējais aritmētiskais
\(t_{\alpha/2,\nu}\) – Stjūdenta kritērija teorētiskā vērtība
\(\nu= n-1\) – brīvības pakāpju skaits
\(s_{\overline{x}}\) – vidējā aritmētiskā reprezentācijas rādītājs \(s_{\overline{x}}=\frac{s}{\sqrt{n}}\)
\(\mu\) - ģenerālkopas vidējais aritmētiskais.
Vidējā aritmētiskā reprezentācijas rādītāju sauc arī par vidējā aritmētiskā standartkļūdu, un tas parāda, cik precīzi paraugkopas dati raksturo ģenerālkopas datus.
6.2.2 Ticamības intervālu aprēķināšana
Vidējā aritmētiskā ticamības intervālu var aprēķināt gan izmantojot gatavas funkcijas, gan arī izmantojot aprēķina formulas. Stjūdenta kritērija teorētisko vērtību aprēķina ar funkciju qt(), kurai kā pirmais arguments jānorāda \((1-\alpha/2)\) (šoreiz izvēlamies strādāt pie ticamības līmeņa 99%) un otrais arguments ir brīvības pakāpju skaits (49). Vidējā aritmētiskā reprezentācijas rādītāju aprēķina kā standartnovirze dalīts ar kvadrātsakni no novērojumu skaita. Pēc tam ticamības intervāla augšējo un apakšējo robežu iegūst pieskaitot vai atņemot robežas vērtību no vidējā aritmētiskā. Piemēram izmantots niedru lapu garums.
robeza<-qt((1-0.01/2),49)*(sd(niedr$garums))/sqrt(50)
augsa<-mean(niedr$garums)+robeza
apaksa<-mean(niedr$garums)-robeza
round(apaksa,2)## [1] 33.69round(augsa,2)## [1] 41.5Secinājums: 99% ticamības intervāls niedru lapu garuma vidējam aritmētiskajam ir ni 33,69 līdz 41,50 cm.
Ticamības intervālu vidējām aritmētiskajam var aprēķināt arī ar funkciju t.test(), kurai kā argumentus norāda kolonnu/vektoru, kuram jāaprēķina ticamības intervāls, kā arī vēlamais ticamības līmenis (conf.level=). Funkcijas rezultātu ir vēlams saglabāt kā atsevišķu objektu. Ar funkciju names() apskatot objekta struktūru nosaukumus, var redzēt, ka ir atsevišķs objekts ar nosaukumu conf.int. To var atlasīt izmantojot $ zīmi. Iegūtais rezultāts ir identisks tam, kuru ieguva izmantojot formulas.
tests<-t.test(niedr$garums,conf.level=0.99)
names(tests)## [1] "statistic" "parameter" "p.value" "conf.int" "estimate"
## [6] "null.value" "alternative" "method" "data.name"round(tests$conf.int,2)## [1] 33.69 41.50
## attr(,"conf.level")
## [1] 0.996.2.3 Bootstrap ticamības intervāli
Atsevišķos gadījumos ticamības intervālus nepieciešams aprēķināt rādītājiem, kuriem nav izstrādātā formula, vai arī zināmiem rādītājiem nevar izmantot parastos aprēķina veidus, jo tiek pārkāpti kādi pieņēmumi par datiem, piemēram, to homogenitāti. Šādos gadījumos var izmantot tā saukto bootstrap metodi. Metodes pamātā ir tas, ka no esošajiem datiem veido daudzas jaunas paraugkopas, kuru apjoms ir vienāds ar oriģinālajiem datiem. Jaunu paraugkopu veidošana notiek pēc paraugošanas ar aizvietošanu principa, tas ir, katra no oriģinālajām vērtībām var tik izraudzīta vairāk kā vienu reizi. Pēc tam katrai no jaunajām paraugkopām aprēķina interesējošo rādītāju un tad aprēķina ticamības intervālu, piemēram, balstoties uz procentilēm.
Lai izmantotu bootstrap metodi programmā R, ir izveidota tam īpaši paredzēta pakete boot (Canty and Ripley 2012). Piemērā aprēķināts ticamības intervāls tiem pašiem niedru lapu garumiem. Sākumā ar funkcijuset.seed() tiek panākts, lai rezultāts būtu identisks piemēram. Tālāk ir jānodefinē funkcija, kas aprēķina vēlamo rādītāju. Šo funkciju nosaucam par videjie un tai būs divi mainīgie - data un indices, kuru radīs funkcija boot(). indices norādīs indeksus, lai atlasītu skaitļus no mainīgā data. Jaunie skaitļi tiks saglabāti mainīgajā d un šim mainīgajam aprēķinās vidējo aritmētisko. Tālāk izmanto funkciju boot(), kurai kā argumentus norādā oriģinālo skaitļu rindu/kolonnu, aprēķināmo rādītāju (funkcija videjie), kā arī veidojamo paraugu skaitu (šoreiz 1000).
set.seed(1234)
library(boot)
videjie<-function(data,indices){
d<-data[indices]
mean(d)
}
dat<-boot(data=niedr$garums,statistic=videjie,R=1000)Ar funkciju boot() izveidoto objektu var apskatīt arī grafiski (6.1 attēls) - redzams, ka iegūtie vidējie aritmētiskie apmēram veido normālo sadalījumu
plot(dat)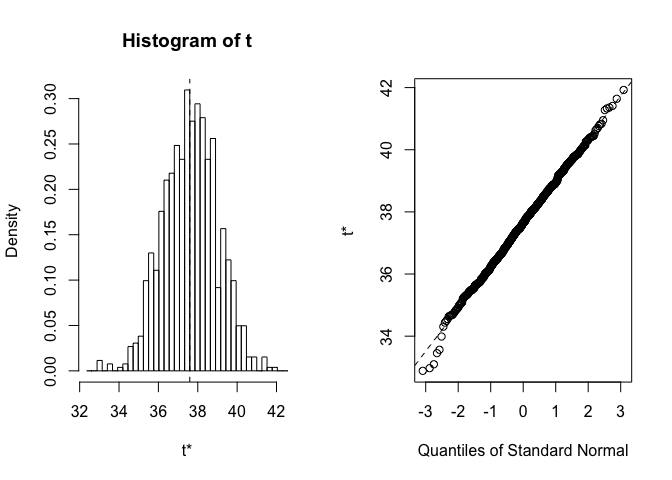
Figure 6.1: Bootstrap vidējo aritmētisko histogramma un QQ grafik
Bootstrap ticamības intervālu aprēķināšanai izmanto funkciju boot.ci(), kurai kā argumentus norāda boot() izveidoto objektu, kā arī vēlamo ticamības līmeni (conf=). Funkcija aprēķina vairākus ticamības intervāla veidus (Manly 2007), kas dod samērā līdzīgus rezultātus.
boot.ci(dat,conf=0.99)## Warning in boot.ci(dat, conf = 0.99): bootstrap variances needed for
## studentized intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = dat, conf = 0.99)
##
## Intervals :
## Level Normal Basic
## 99% (34.04, 41.09 ) (33.86, 41.62 )
##
## Level Percentile BCa
## 99% (33.56, 41.33 ) (33.39, 41.11 )
## Calculations and Intervals on Original Scale
## Some basic intervals may be unstable
## Some percentile intervals may be unstable
## Some BCa intervals may be unstable6.2.4 Ticamības intervālu grafiskais attēlojums
Izmantojot funkcijas, kas pieejamas paketē plotrix (Lemon 2006), ir iespējams izveidot grafiku ar ticamības intervāliem. Pirmkārt, ir nepieciešams objekts, kas satur vidējos aritmētiskos. Piemēram izmantots niedru lapu garums, kas aprēķināts katram no parauglaukumiem.
videjie<-tapply(niedr$garums,niedr$paraug,mean)
videjie## Austr Riet Ziem
## 33.52941 41.05294 38.23750Pēc tam jāizveido objekts, kas satur skaitļus Stjūdenta kritērija un videjā aritmētiskā reprezentācijas rādītāja reizinājumus. Tam izmanto atkal funkciju tapply(), tikai beigās norāda paša definētu funkciju.
vid.rob<-tapply(niedr$garums,niedr$paraug,
function(x) (qt((1-0.01/2),length(x))*sd(x)/sqrt(length(x))))
vid.rob## Austr Riet Ziem
## 6.234850 6.590739 8.547961Grafika ar ticāmības intervāliem izveidošanai (6.2 attēls) jāizmanto funkcija plotCI(), kurai kā argumentus jānorāda x mainīgais (šoreiz skaitļi no 1 līdz 3, jo ir trīs parauglaukumi), pēc tam jānorāda vektors ar vidējiem aritmētiskajiem, vektors ar Stjūdenta kritērija un videjā aritmētiskā reprezentācijas rādītāja reizinājumiem, kā arī var norādīt papildus argumentus grafika izskata uzlabošanai.
library(plotrix)
plotCI(1:3,as.vector(videjie),as.vector(vid.rob),axes=FALSE,
xlab="Puse",ylab="Videjais garums",ylim=c(0,50),lwd=2)## Warning in plot.xy(xy.coords(x, y), type = type, ...): "axes" is not a
## graphical parameteraxis(1,at=1:3,labels=c("A","R","Z"))
axis(2,at=seq(0,50,10))
box()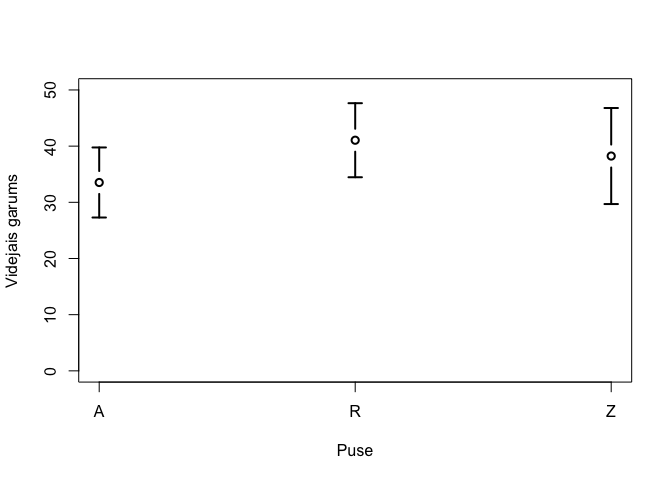
Figure 6.2: Vidējais niedru lapu garums trīs parauglaukumos ar 99% ticamības intervāliem