11. nodaļa. Kovariācijas analīze
11.1 Teorētiskais pamatojums
Vēl jāuraksta!
11.2 Dati
Kovariācijas analīzes piemēram izmantosim datus no faila dieta.txt no pētījuma par to, vai svara samazinājums ir lielāks tad, ja ievēro diētu vai arī diētu kopā ar sportošanu (mainīgais metode). Par katru pētījumā iesaistīto cilvēku ir zināms tā sākotnējais svars un pētījumā laikā uzrādītais svara samazinājums.
dieta<-read.table(file="dieta.txt",header=T,sep="\t",dec=".")
str(dieta)## 'data.frame': 42 obs. of 3 variables:
## $ svars : num 60 62.5 65 67.5 70 72.5 75 77.5 80 82.5 ...
## $ metode : Factor w/ 2 levels "esana","kopa": 2 2 2 2 2 2 2 2 2 2 ...
## $ samazinajums: num 4.2 5.4 2.8 8.2 5 8.4 9.6 8.5 6.7 7.1 ...summary(dieta)## svars metode samazinajums
## Min. : 60.00 esana:21 Min. : 2.800
## 1st Qu.: 85.62 kopa :21 1st Qu.: 5.425
## Median :100.00 Median : 7.900
## Mean :100.00 Mean : 7.502
## 3rd Qu.:114.38 3rd Qu.: 9.600
## Max. :140.00 Max. :14.40011.3 Dispersijas analīze
Pirmais variants kādā veidā varētu analizēt šos datus, ir izmantot dispersijas analīzi, kur kā atkarīgais mainīgais ir samazinajums, bet neatkarīgais mainīgais ir metode. Šoreiz dispersijas analīzes veikšanai izmantota cita pieeja - ar funkcijām lm() un anova(), kas dod vienādu rezultātu kā funkcija aov().
mod<-lm(samazinajums~metode,data=dieta)
anova(mod)## Analysis of Variance Table
##
## Response: samazinajums
## Df Sum Sq Mean Sq F value Pr(>F)
## metode 1 19.339 19.3393 2.9155 0.09548 .
## Residuals 40 265.330 6.6333
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Secinājums: dispersijas analīzes rezultāti parāda, ka faktora metode ietekme nav statistiski būtiska (p-vērtība ir lielāka par 0,05). Ja aspkatām abu metožu vidējās vērtības, kā arī vērtību grafisko attēlojumu (11.1 attēls), var redzēt, ka starp abām grupām ir neliela starpība, bet vienlaicīgi arī vērojama izteikta vērtību pārklāšanās.
with(dieta,tapply(samazinajums,metode,mean))## esana kopa
## 6.823810 8.180952with(dieta,boxplot(samazinajums~metode))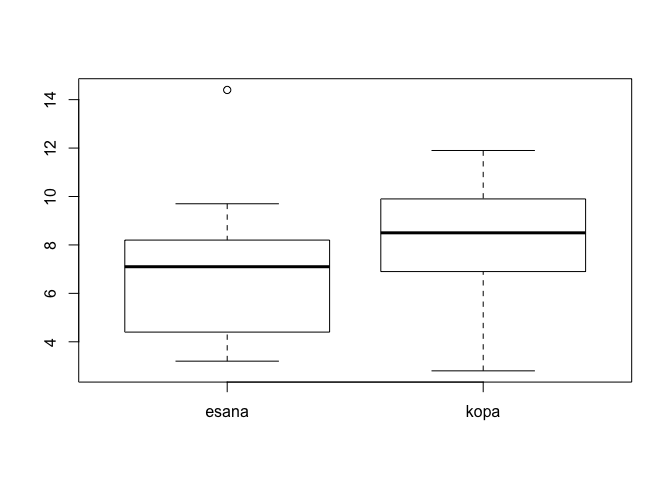
Figure 11.1: Box-plot grafiks svara samazinājumam atkarībā no diētas veida
11.4 Kvantitatīva mainīgā iekļaušana modelī
Ja vienīgais statistiskais tests, kuru izvēlētos veikt šajā pētījumā būtu dispersijas analīze, tad paliktu pie secinājuma, ka diētas metodes savā starpā neatšķiras. Bet būtiski ir ņemt vērā arī to, ka ir pieejami dati arī par katra cilvēka sākotnējo svaru, turklāt šis sākotnējais svars katrā grupā ir atšķirīgs. Lai pārbaudītu vai šai papildus informācijai (cilvēka sākotnējais svars) ir būtiska ietekme uz to, kādu efektu dod diētas metode, var veikt kovariācijas analīzi. Šajā analīzē mēs pārbaudam viena vai vairāku faktoru ietekmi, vienlaicīgi ņemot vērā vēl cita kvantitatīvā mainīgā vērtības. Kovariācijas analīzi veic ar funkciju lm(), vienlaicīgi norādot abus mainīgo veidus. Rezultātu apskatīšanai izmanto funkcijas anova() un summary().
mod1<-lm(samazinajums~metode+svars,data=dieta)
anova(mod1)## Analysis of Variance Table
##
## Response: samazinajums
## Df Sum Sq Mean Sq F value Pr(>F)
## metode 1 19.339 19.339 5.3628 0.02592 *
## svars 1 124.688 124.688 34.5757 7.6e-07 ***
## Residuals 39 140.643 3.606
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Secinājums: Iekļaujot modelī arī sākotnējo svaru, redzams, ka tagad pastāv statistiski būtiska atšķirība starp diētas veidiem (p-vērtība 0,026), kā arī sākotnējam svaram ir būtiska ietekme uz to, kāds ir svara samazinājums.
Analīzes rezultātu apskatot ar funkciju summary(), var iegūt atbilstošos lineāra modeļa koeficientus. Šeit svarīgi ņemt vērā to, ka kvalitatīvais mainīgais tiek pārkodēts pēc principa, ka alfabētiski pirmais mainīgā līmenis (šajā gadījumā esana) tiek izmantots kā references līmenis, bet visi pārējie līmeņi tiek salīdzināti ar šo līmeni.
summary(mod1)##
## Call:
## lm(formula = samazinajums ~ metode + svars, data = dieta)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8419 -1.4185 -0.2487 1.2422 5.0153
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -6.26528 2.26424 -2.767 0.0086 **
## metodekopa 4.77169 0.82502 5.784 1.03e-06 ***
## svars 0.11382 0.01936 5.880 7.60e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.899 on 39 degrees of freedom
## Multiple R-squared: 0.5059, Adjusted R-squared: 0.4806
## F-statistic: 19.97 on 2 and 39 DF, p-value: 1.068e-06Secinājums: sākotnējam svaram ir pozitīvs efekts uz svara samazinājumu, tas ir, jo lielāks ir sākotnējais svars, jo lielāks ir absolūtais svara samazinājums. Koeficients pie (Intercept) (b0) atbilst situācijai, kad diētas metode bija esana, bet metodei kopa b0 vērtība veidojas saskaitot koeficientus pie (Intercept) un pie metodekopa. Koeficients pie metodekopa ir būtisks, tas ir, pastāv statistiski būtiska atšķirība starp svara samazinājumu starp abām šīm diētas metodēm pie vienāda sākotnējā svara un šī starpība ir 4,77 kg.
Kovariācijas analīzē var pārbaudīt arī situāciju, kad ir ne tikai atšķirīga b0 koeficienta vērtība starp gradācijas klasēm, bet arī to vai ir būtiska atšķirība starp b1 koeficientiem (regresijas taišņu slīpumiem) starp gradācijas klasēm. Šī pētījuma kontekstā mēs varētu pārbaudīt vai pie dažādiem diētas veidiem ir vērojama atšķirīga saistība starp sākotnējo svaru un svara samazinājumu. Šādas analīzes veikšanai sākotnējā modelī ir jaiekļauj iedarbība (interaction) starp abiem mainīgajiem, ko panāk starp tiem norādot * zīmi.
mod2<-lm(samazinajums~metode*svars,data=dieta)
anova(mod2)## Analysis of Variance Table
##
## Response: samazinajums
## Df Sum Sq Mean Sq F value Pr(>F)
## metode 1 19.339 19.339 5.3279 0.02652 *
## svars 1 124.688 124.688 34.3511 8.832e-07 ***
## metode:svars 1 2.710 2.710 0.7466 0.39299
## Residuals 38 137.933 3.630
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Secinājums: mainīgajam metode:svars nav statistiski būtiska ietekme uz svara samazinājumu, tas ir, nav atšķirības tajā kāda ir saistība starp sākontējo svaru un svara samazinājumu atkarībā no diētas veida.
Ar funkcijas AIC() palīdzību var salīdzināt visus trīs modeļus kopā. Viszemākā AIC vērtība (attiecīgi labākais modelis) ir mod1, kurā bija iekļauti abi faktori bez savstarpējās iedarbības.
AIC(mod,mod1,mod2)## df AIC
## mod 3 202.6097
## mod1 4 177.9501
## mod2 5 179.1329Kovariācijas analīzes rezultātus vislabāk apskatīt grafiski (11.2 attēls). Kā pirmo soli radām mainīgo jauns, kas satur svara vērtības no 60 līdz 140 ik pa pieci - kopā 17 vērtības. Pēc tam ar funkciju predict() aprēķina prognozētās svara samazinājuma vērtības atsevišķi katrai no diētas metodēm. Ar funkciju uzzīmē izkliedes grafiku starp oriģinālajām svara samazinājuma un sākotnējā svara vērtībām, turklāt simbola veids ir atkarīgs no diētas metodes. Pēc tam attēlam pa virsu uzliek trenda līnijas katrai no metodēm izmantojot funkciju lines(). Nepārtraukta līnija ir metodei kopa, bet raustīta līnija ir metodei esana.
jauns<-seq(60,140,5)
pred.esana<-predict(mod1,data.frame(svars=jauns,metode=rep("esana",17)))
pred.kopa<-predict(mod1,data.frame(svars=jauns,metode=rep("kopa",17)))
plot(dieta$samazinajums~dieta$svars,pch=as.numeric(dieta$metode),xlab="Sakotnejais svars",ylab="Svara samazinajums")
lines(pred.kopa~jauns,lty=1)
lines(pred.esana~jauns,lty=2)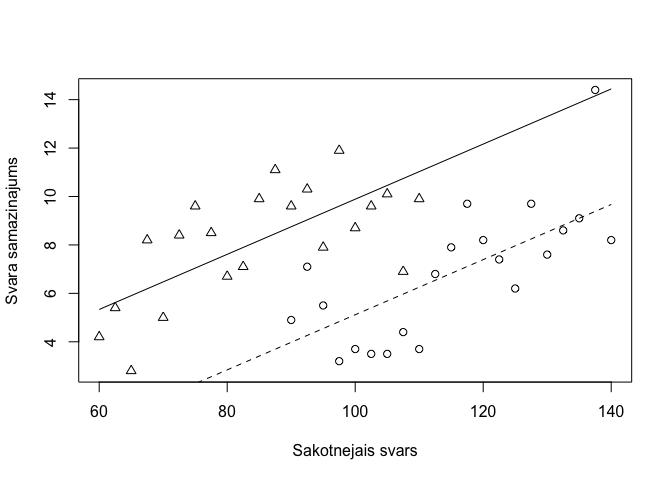
Figure 11.2: Izkliedes grafiks ar trenda līnijām starp sākotnējo svaru un svara samazinājumu atkarībā no diētas veida