5. nodaļa. Datu izzināšana un normalitātes testi
5.1 Datu izzināšana
Pirms uzsākt reālu datu analīzi, veicot dažādus statistiskos testus, vienmēr vajag sākotnējo datu izzināšanu, izmantojot dažādus datu grafiskos attēlojumus. Tādējādi ir iespēja jau pirms statistisko analīžu veikšanas novērtēt vai datos redzamas kādas tendences, savstarpējās saistības, grupēšanās, kā arī secināt vai datos nav kādas dīvainas, neiederīgas vērtības.
Kā piemērs izmantots datu fails niedres2.txt, kas satur informāciju par niedru lapu garumu un platumu trīs parauglaukumos.
niedr<-read.table(file="niedres2.txt",header=T,sep="\t",dec=".")
str(niedr)## 'data.frame': 50 obs. of 3 variables:
## $ garums : num 31.6 23.2 39.2 37.4 21.1 37 24.7 31.3 37.4 39.7 ...
## $ platums: num 2.5 2.3 2.1 5.8 2.2 4.1 3.5 4.2 2.5 2.8 ...
## $ paraug : Factor w/ 3 levels "Austr","Riet",..: 1 1 1 1 1 1 1 1 1 1 ...Vienkāršākais grafiks datu apskatīšanai ir izkliedes grafiks, ko programmā R var iegūt ar funkciju plot(). Šajā grafikā (5.1 attēls) uz x ass atlikts novērojuma kārtas numurs, uz y ass novērojumu vērtības. Pēc izkliedes grafika var gūt priekštatu par vērtību izkliedi, gan arī novērtēt vai nav kādas ekstremāli mazas vai lielas vērtības.
plot(niedr$garums)
Figure 5.1: Viena mainīgā izkliedes grafiks
Ja funkcijā plot() norāda divus mainīgos, tad vienlaicīgi var novērtēt gan šo mainīgo vērtību saistību (5.2 attēls), gan arī pamanīt kādus ekstrēmus, ko nav iespējams novērtēt skatot katru mainīgo atsevišķi.
plot(niedr$garums,niedr$platums)
Figure 5.2: Divu mainīgo izkliedes grafiks
Box-plot grafiki, ko iegūst ar funkciju boxplot(), ir piemēroti, lai novērtētu vērtību izkliedi datos (5.3 attēls). Box-plot grafikā līnija, kas atrodas taisntūra vidū, atbilst mediānai, taisnstūra apakšējā un augšējā mala attiecīgi ir 1. un 3. kvartile. Apakšējā un augšējā līnija attiecīgi ir minimālā un maksimālā vērtība datos, ar piebildi, ka šīs līnijas neatrodas tālāk kā 1,5 reiz taisntūra platums (attālums starp 1. un 3. kvartili). Ja minimālā vai maksimālā vērtība ir tālāk nekā šīs 1,5 reizes, tad šos novērojumus apzīmē ar punktu.
boxplot(niedr$garums)
Figure 5.3: Box-plot grafiks vienam mainīgajam
Ja funkcijā {boxplot() norāda mainīgo, kas satur dalījumu līmeņos, tad atsevišķš grafiks tiek izveidots katram no dalījuma līmeņiem (5.4 attēls). Pēc šī grafika var salīdzināt datu izkliedi uzreiz vairākiem līmeņiem.
boxplot(niedr$garums~niedr$paraug)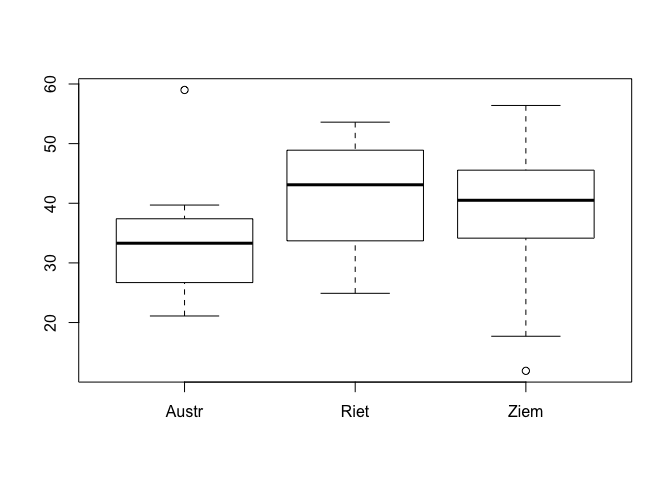
Figure 5.4: Box-plot grafiks trīs paraugkopām
Gadījumos, kad novērojumu skaits ir salīdzinoši mazs, tad labāk datu izkliedi raksturo punktu grafiks (5.5 attēls), ko var iegūt ar funkciju stripchart(). Šajā grafikā katrs novērojums ir attēlots ar kvadrātiņi un visi novērojumi izkārtoti vienā strīpā.
stripchart(niedr$garums)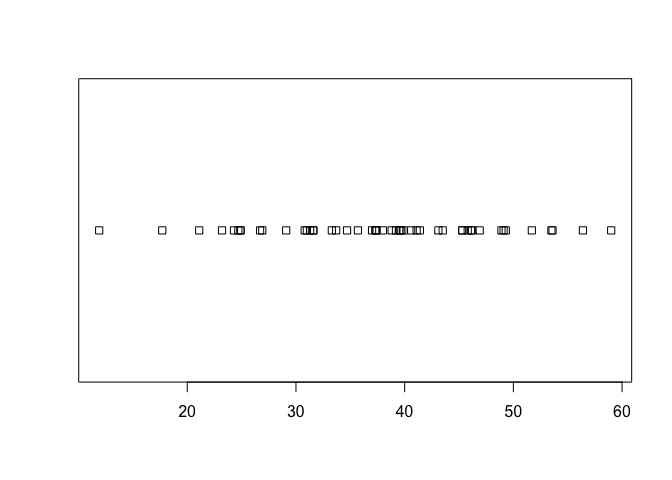
Figure 5.5: Punktu grafiks
Ja novērojumi pārklājas un nav iespējams precīzi attēlā novērtēt, cik daudz novērojumu atbilst katrai vērtībai, funkciju stripchart() var papildināt ar argumentu method="stack", kas novietot kvadrātiņus blakus, ja tie pilnībā pārklājas (5.6 attēls). Arguments vert=T nodrošina, ka grafiks novietojas vertikāli, nevis horizontāli.
stripchart(niedr$garums,method="stack",vert=T)
Figure 5.6: Modificēts punktu grafiks
Vēl viens plaši izmantots datu attēlošanas veids ir histogramma, ko programmā R var izveidot ar funkciju hist(). Histogrammā dati tiek sadalīti klasēs un tādējādi var novērtēt vērtību sadalījuma veidu - vienmērīgi, zvanveidīgi, ar izteiktām minimālām vai maksimālām vērtībām (5.7 attēls). Funkcijai var mainīt argumentus gan nosakat cik klasēs dalīt datus, gan arī nosakot tieši dalījuma robežas.
hist(niedr$garums)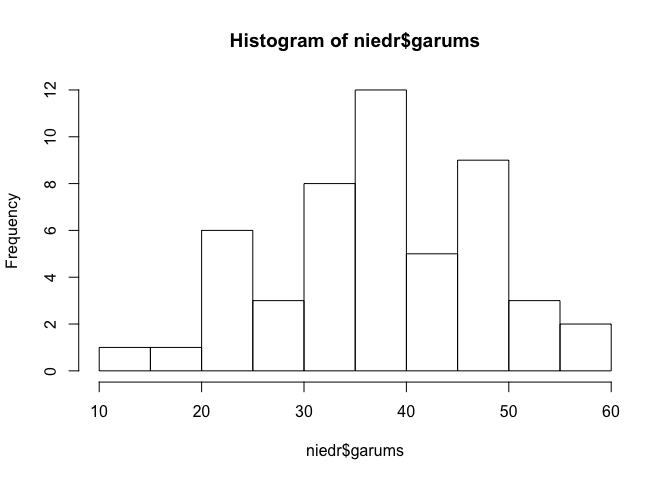
Figure 5.7: Pazīmes niedru lapu garums histogramma
5.2 Normalitātes testi
5.2.1 Grafiskā analīze
Daudzu statistisko metožu pieņēmums ir, ka analizējamie dati nāk no ģenerālkopas, kura atbilst normālajam sadalījumam. Lai par to pārliecinātos, ir jāveic noteikti statistiskie testi. Jaunākajā statistiskajā literatūrā arvien biežāk kā pamatmetode normalitātes novērtēšanai tiek izmantota grafiskā analīzē, nevis analītiskie testi.
Viens no grafiku veidiem, ko izmantot normalitātes novērtēšanai, var būt histogramma (5.7 attēls). Histrogrammai ir jāveido apmēram zvanveidīgs izskats, lai pieņemtu, ka dati atbilst normālajam sadalījumam. Ar šo grafiku veidu problēma ir tā, ka histogrammas izskats lielā mērā būs atkarīgs no tā, cik klasēs dati ir sadalīti.
Uzticamāks grafika veids ir tā saukti QQ grafiki, kas attēlo attiecību starp reālo datu kvantilēm un teorētisko datu kvantilēm (teorētiskie dati veidoti balstoties uz reālo datu statistiskajiem rādītājiem tā, lai tie atbilstu normālajam sadalījumam). Ja reālie dati atbilst normālajam sadalījumam, tad grafikā visi punkti novietojas uz diagonāles. Programmā R QQ grafiku veido ar funkciju qqnorm(), kurai kā argumentu norāda reālos datus. Papildus var izmantot arī funkciju qqline(), kas novelk līniju, lai būtu vieglāk interpretēt rezultātus. Iegūtajā grafikā (5.8 attēls) ideālā gadījumā visiem punktiem būtu jāatrodas uz taisnes, bet nelielas novirzes arī ir akceptējamas. Lai iemācītos strādāt ar šādiem grafikiem, var ģēnerēt mākslīgus datus no normālā sadalījuma un skatīties kā kātreiz izskatās QQ grafiks.
qqnorm(niedr$garums)
qqline(niedr$garums)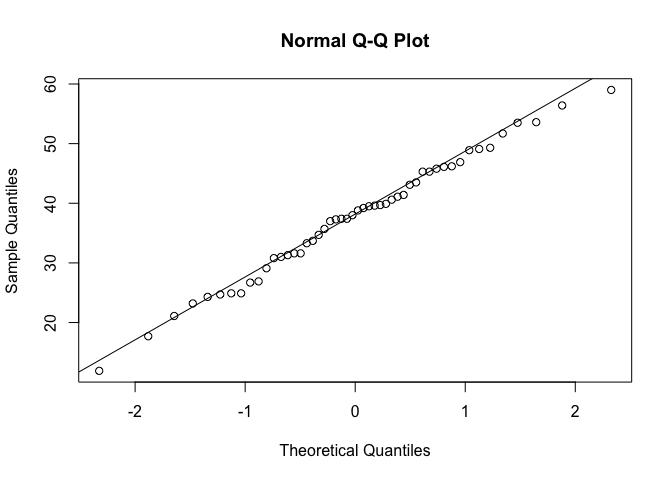
Figure 5.8: QQ grafiks niedru lapu garumam
Paketē car ir funkcija qqPlot(), kas arī veido QQ grafiku, tikai tas ir papildināts ar līnijām, kas parāda 95% ticamības intervālu (5.9 attēls), tādējādi atvieglojot interpretāciju. Ja visi punkti atrodas starp raustītajām līnijām, tad ar 95% pārliecību var apgalvot, ka dati nāk no ģenerālkopas, kas atbilst normālajm sadalījumam.
library(car)
qqPlot(niedr$garums)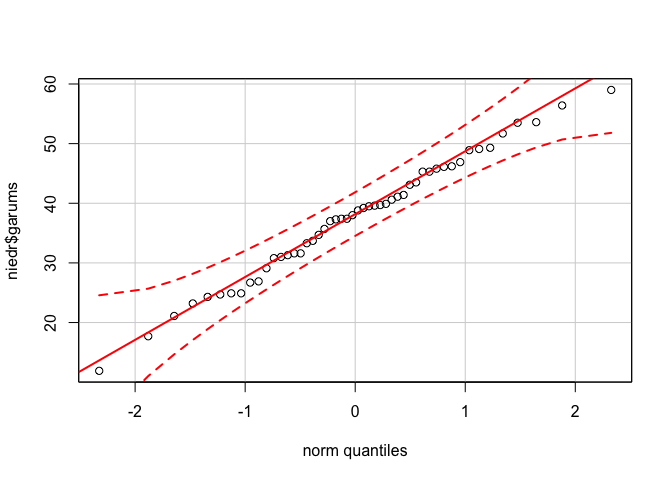
Figure 5.9: Modificēts QQ grafiks niedru lapu garuma
5.2.2 Analītiskā analīze
Ja ir nepieciešams daudz formālāks veids kā novērtēt datu atbilstību normālajam sadalījumam, var izmantot kādu no analītiskajām metodēm. R bāzes versijā ir pieejams Šapiro-Vilka normalitātes tests, ko var iegūt ar funkciju shapiro.test(). Funkcijai kā arguments jānorāda tikai mainīgais, kuram veikt normalitātes testu. Nulles hipotēze par to, ka dati atbilst normālajam sadalījumam nebūs noraidīta, ja iegūtā p-vērtība būs lielāka par izvēlēto būtiskuma līmeni.
shapiro.test(niedr$garums)##
## Shapiro-Wilk normality test
##
## data: niedr$garums
## W = 0.99101, p-value = 0.9668Secinājums: pie būtiskuma līmeņa \(\alpha=0,05\) pazīmes niedru lapu garums vērtības atbilst normālajam sadalījumam, jo p-vērtība ir lielāka par noteikto būtiskuma līmeni (0,97>0,05).
Funkciju shapiro.test() var izmantot arī kopā ar funkciju tapply(), tādējādi veicot šo testu vairākiem dalījuma līmeņiem uzreiz.
tapply(niedr$garums,niedr$paraug,shapiro.test)## $Austr
##
## Shapiro-Wilk normality test
##
## data: X[[i]]
## W = 0.8863, p-value = 0.04028
##
##
## $Riet
##
## Shapiro-Wilk normality test
##
## data: X[[i]]
## W = 0.94264, p-value = 0.3508
##
##
## $Ziem
##
## Shapiro-Wilk normality test
##
## data: X[[i]]
## W = 0.90337, p-value = 0.09103Secinājums: pie būtiskuma līmeņa \(\alpha=0,05\) pazīmes niedru lapu garums vērtības atbilst normālajam sadalījumam Rietumu un Ziemeļu parauglaukumos, jo p-vērtības ir lielākas par noteikto būtiskuma līmeni (0,35>0,05 un 0,09>0,05), toties Austrumu parauglaukuma dati neatbilst normālajam sadalījumam, jo p-vertība ir mazāka par noteikto būtiskuma līmeni (0,04<0,05).
Programmā R ir pieejama pakete nortest, kurā ir apvienoti pieci dažādi normalitātes testi, piemēram, Andersona-Darlinga tests un Lilliefora (Kolmogorova-Smirnova) tests. Testi savā starpā atšķiras ar algoritmiem kādā veidā salīdzina reālos datus ar teorētiski sagaidāmajiem, attiecīgi arī iegūtās p-vērtības starp testiem mēdz atšķirties. Daļa no testiem ir striktāki, daļa mazāk strikti.
library(nortest)
ad.test(niedr$garums)##
## Anderson-Darling normality test
##
## data: niedr$garums
## A = 0.17373, p-value = 0.9223