10. nodaļa. Regresijas analīze
10.1 Teorētiskais pamatojums
Vēl jāuzraksta!
Plašāku pamatojumu, kā arī piemērus par regrijas analīzi var atrast Faraway (2005), Vittinghoff et al. (2005).
10.2 Dati
Regresijas analīzes piemēram izmantosim datu no datus faila augi2.txt. Šajā failā ir informācija no augu audzēšanas eksperimenta 45 parauglaukumos. No katra parauglaukuma ir informācija par nokrišņu daudzumu jūnijā, jūlija un augustā, kā arī visā augšanas sezonā kopā, vidējais gaismas daudzums sezonā, augsnes pH un kopējā augu biomasa katrā no parauglaukumiem. Izmantojot funkciju summary() var apskatīt visu parametru vērtību izkliedi un raksturojumu.
augi2<-read.table(file="augi2.txt",header=TRUE,sep="\t",dec=".")
str(augi2)## 'data.frame': 45 obs. of 7 variables:
## $ jun.nokr: num 78.2 79.7 76 65.7 82.4 92 64.2 40.1 87.5 66.2 ...
## $ jul.nokr: num 48.4 80.2 58.8 103.5 37 ...
## $ aug.nokr: num 100.3 34.8 79.6 64.4 70.1 ...
## $ sezona : num 276 252 267 279 239 ...
## $ gaisma : int 57 42 77 89 79 89 86 85 93 72 ...
## $ pH : num 7.19 6.69 6.99 6.7 6.56 6.33 7.01 6.38 6.65 6.95 ...
## $ biomasa : num 37.2 30.6 36.3 59.9 32.9 44.7 43.7 51.6 53.8 44.3 ...summary(augi2)## jun.nokr jul.nokr aug.nokr sezona
## Min. : 40.10 Min. : 26.5 Min. : 34.80 Min. :170.6
## 1st Qu.: 60.10 1st Qu.: 45.5 1st Qu.: 58.90 1st Qu.:221.4
## Median : 73.40 Median : 51.6 Median : 66.90 Median :248.0
## Mean : 71.66 Mean : 55.9 Mean : 67.59 Mean :244.4
## 3rd Qu.: 82.40 3rd Qu.: 66.9 3rd Qu.: 76.40 3rd Qu.:268.0
## Max. :106.20 Max. :103.5 Max. :100.30 Max. :303.7
## gaisma pH biomasa
## Min. :35.00 Min. :6.330 Min. :14.20
## 1st Qu.:55.00 1st Qu.:6.630 1st Qu.:32.90
## Median :72.00 Median :6.820 Median :39.50
## Mean :68.96 Mean :6.796 Mean :38.74
## 3rd Qu.:85.00 3rd Qu.:7.010 3rd Qu.:44.30
## Max. :96.00 Max. :7.190 Max. :59.9010.3 Pāru regresija
Lineārās pāru regresijas veikšanai izmanto funkciju lm(), kurai kā pirmo argumentu norāda regresentu jeb atkarīgo mainīgo, tad nāk tildes zīme un viens vai vairāki regresori jeb atkarīgie mainīgie. Ja ir vairāk kā viens regresors, tad tos atdala ar plus zīmi. Kā pēdējais arguments jānorāda datu tabulu, no kuras jāņem dati. Regresijas analīzes rezultātu apskatīšanai jāizmanto funkcija summary(), kurai kā argumentu norāda objektu, kas satur regresijas analīzes modeli. Analīzes rezultātos ir vairākas sadaļas: (a) Residuals: atlikuma vērtību raksturojums; (b) Coefficients: regresijas vienādojuma koeficientu raksturojums - Estimate ir aprēķinātie regresijas vienādojuma koeficienti - (Intercept) - koeficients b0, vērtība pie regresora nosaukuma ir koeficients b1 jeb slīpuma vērtība (slope); Std.Error - koeficientu standartkļūdas, t value - atbilstošā T vērtība katram koeficientam un Pr(>|t|) ir atbilstošā p-vērtība novērtējot katram koeficienta būtiskumu atsevišķi; (c) apakšējā daļā ir visa modeļa kopējais novērtējums - atlikuma standartkļūda un brīvības pakāpju skaits, determinācijas koeficients un pielāgotais determinācijas koeficients, F vērtība un p-vērtība visam modelim kopumā.
mod1<-lm(biomasa~gaisma,data=augi2)
summary(mod1)##
## Call:
## lm(formula = biomasa ~ gaisma, data = augi2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.6391 -3.8922 -0.5067 4.5209 14.7037
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 15.10044 3.86300 3.909 0.000324 ***
## gaisma 0.34276 0.05411 6.334 1.19e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.709 on 43 degrees of freedom
## Multiple R-squared: 0.4827, Adjusted R-squared: 0.4707
## F-statistic: 40.12 on 1 and 43 DF, p-value: 1.193e-07Secinājumi: iegūtais regresijas modelis ir biomasa=15,10044 + 0.34276*gaisma, tas ir, gaismas daudzumam ir pozitīva ietekme uz biomasas pieaugumu. Gan viss regresijas modelis, gan arī atsevišķi katrs no regresijas koeficientiem šajā gadījumā ir statistiski būtiski, jo atbilstošās p-vērtības ir mazākas par būtiskuma līmeni. Dotais regresijas modelis izskaidro 47,07% no regresenta jeb biomasas vērtību variēšanas.
Regresijas analīzes rezultātu attēlošanai vai izveidot grafiku, kur reālie novērojumi ir attēloti kā punkti, bet papildus pievienota regresijas taisne (10.1 attēls). Šīs taisnes pievienošanai jāizmanto funkcija abline() kopā ar funkciju lm().
plot(augi2$biomasa~augi2$gaisma,xlab="Gaismas daudzums",ylab="Augu biomasa")
abline(lm(augi2$biomasa~augi2$gaisma))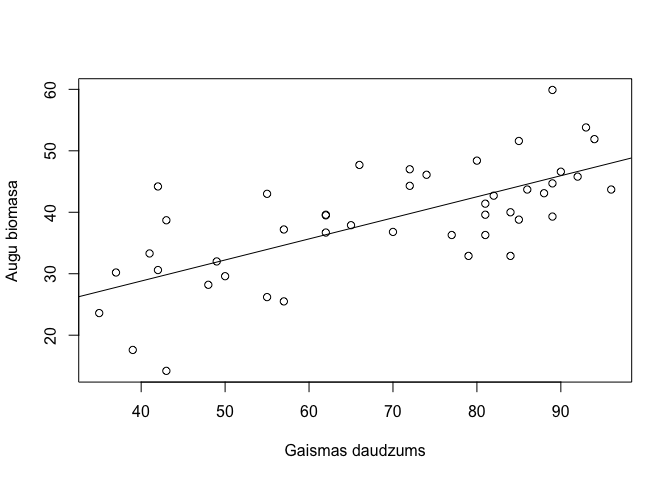
Figure 10.1: Izkliedes grafiks starp pazīmēm gaisma un biomasa ar pievienotu regresijas līkni
10.4 Regresijas analīzes pieņēmumu pārbaude
Lai arī regresijas analīzē tiek konstatēts, ka modelis ir statistiski būtisks, tas nav analīzes noslēdzošais posms. Papildus ir jāpārbauda vai tiek ievēroti visi regresijas analīzes pieņēmumi. Viens no veidiem tā paveikšanai ir izmantot grafiskās iespējas. Ja funkcijā plot() kā argumentu norāda regresijas analīzes modeli, tad iegūst četrus diagnosticējošos grafikus. Visu četru grafiku vienlaicīgai apskatīšanai papildus jāizmanto funkcija par() ar argumentu `mfrow=’. Iegūtajos attēlos (10.2 attēls) pirmajā kolonnā ir redzamas atlikuma vērtības attiecībā pret prognozētajām vērtībām un standartizētās atlikuma vērtības attiecībā pret prognozētajām vērtībām. Šajos divos grafikos nedrīkst parādīties nekādas iezīmes, piemēram, trendi, kā arī punktiem ir jābūt nejauši izkārtotiem. Ja ir redzams trends, tas nozīmē, ka ir vēl kāds būtisks faktors, kas nav ņemts vērā. Ja ir vērojama vērtību izkliedes izmaiņas, vai punktu grupēšanās, tad ir problēmas ar dispersiju homogenitāti. Augšējā labējā stūrī ir grafiks, kas parāda standartizēto atlikuma vērtību QQ grafiku. Tas norāda vai atlikuma vērtības atbilst normālajam sadalījumam. Apakšējā labējā stūrī ir grafiks, pēc kura var spriest par katra novērojuma ietekmi uz kopējo modeli. Ja ir kāds punkts, kurš atrodas ārpus raustītajām Cook’s distance līnijām (vērtības virs 0.5 vai virs 1), tad šim novērojumam ir liela ietekme uz kopējo regresijas modeli un tāpēc ir vērts pievērst uzmanību šim novērojumam.
par(mfrow=c(2,2))
plot(mod1)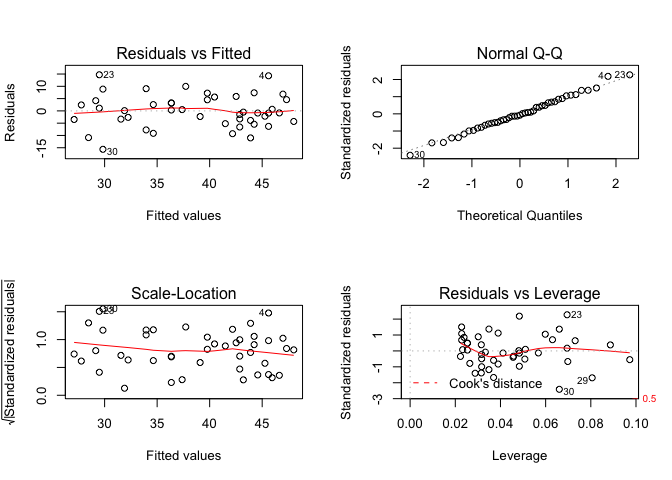
Figure 10.2: Regresijas analīzes diagnosticējošie grafiki
Vēl viens no variantiem, ko var pārbaudīt pēc regresijas analīzes, ir atlikuma vērtību izkliede atkarībā no citiem mainīgajiem, kas netika iekļauti modelī (protams, ja ir dati par šiem citiem mainīgajiem). Arī šajos attēlos nevajadzētu redzēt nekādus trendus, vai punktu grupēšanos. 10.3 attēlā ir samērā skaidri redzama saistība starp jūnija, jūlija un augusta nokrišņu daudzumu un atlikuma vērtībām, kas nozīmē, ka šo faktoru iekļaušana modelī to varētu uzlabot.
atlikums<-resid(mod1)
par(mfrow=c(2,2))
plot(atlikums~augi2$jun.nokr)
plot(atlikums~augi2$jul.nokr)
plot(atlikums~augi2$aug.nokr)
plot(atlikums~augi2$pH)
Figure 10.3: Izkliedes grafiki starp regresijas modeļa atlikuma vērtībām un modelī neiekļautajiem mainīgajiem
10.5 Vērtību prognozēšana
Viens no regresijas modeļu pielietojumiem ir jaunu vērtību prognozēšana. Lai to izdarītu, ir jāizmanto funkcija predict(), kurai kā argumentus jānorāda saglabātais regresijas modelis, kā arī datu tabula, kas satur jaunās vērtības. Papildus var iegūt arī ticamības intervālu šīm prognozētajām vērtībām ar argumentu interval="prediction". Veidojot jauno datu tabulu ir jāatceras, ka tajā obligāti ir jābūt tādiem pašiem kolonnu nosaukumiem, kādi bija regresijas modelī izmantotie regresoru nosaukumi (tabulā drīkst būt arī citas kolonnas).
progn<-data.frame(gaisma=c(10,50,100))
predict(mod1,progn,interval="prediction")## fit lwr upr
## 1 18.52802 3.411995 33.64405
## 2 32.23837 18.404298 46.07245
## 3 49.37631 35.284476 63.4681410.6 Daudzfaktoru regresija
Pirmais solis daudzfaktoru regresijas analīzes veikšanai ir pārliecināšanās vai starp regresoriem nepastāv izteikta kolinearitāte (savstarpējā korelācija), jo tas būtu pārkāpums vienam no daudzfaktoru regresijas pieņēmumiem. Šim uzdevumam var izmantot gan grafisko analīzi, piemēram, ar funkciju pairs(), gan arī aprēķināt korelācijas koeficientus analītiski ar funkciju cor(). Gan no 10.4 attēla, gan arī no korelācijas analīzes rezultātiem ir redzams, ka ir būtiska saistība starp veģetācijas sezonas kopējo nokrišņu daudzumu un atsevišķu mēnešu nokrišņu daudzumu, tāpēc nebūtu ieteicams vienlaicīgi visus šos mainīgos iekļaut regresijas modelī.
pairs(augi2)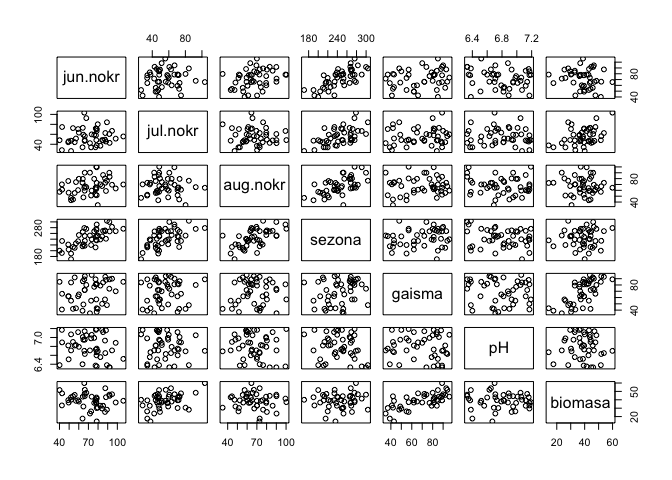
Figure 10.4: Izkliedes grafiki starp visiem datu objekta augi2 mainīgajiem
round(cor(augi2),2)## jun.nokr jul.nokr aug.nokr sezona gaisma pH biomasa
## jun.nokr 1.00 0.11 0.30 0.73 0.22 -0.18 -0.18
## jul.nokr 0.11 1.00 -0.05 0.57 0.11 -0.05 0.41
## aug.nokr 0.30 -0.05 1.00 0.60 0.08 -0.11 -0.08
## sezona 0.73 0.57 0.60 1.00 0.19 -0.19 0.07
## gaisma 0.22 0.11 0.08 0.19 1.00 -0.08 0.69
## pH -0.18 -0.05 -0.11 -0.19 -0.08 1.00 -0.03
## biomasa -0.18 0.41 -0.08 0.07 0.69 -0.03 1.00Daudzfaktoru regresijas analīzes veikšanai izmanto to pašu funkciju lm(), tikai papildus norāda nevis vienu, bet vairākus regresorus, kas savā starpā ir atdalīti ar plus zīmi. Piemērā apskatīts kā augu biomasu ietekmē pieci regresori.
mod2<-lm(biomasa~gaisma+jun.nokr+jul.nokr+aug.nokr+pH,data=augi2)
summary(mod2)##
## Call:
## lm(formula = biomasa ~ gaisma + jun.nokr + jul.nokr + aug.nokr +
## pH, data = augi2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10.054 -3.449 -1.333 3.439 8.766
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.955554 21.640357 1.061 0.295317
## gaisma 0.361933 0.042487 8.519 1.95e-10 ***
## jun.nokr -0.221332 0.052954 -4.180 0.000159 ***
## jul.nokr 0.200221 0.046717 4.286 0.000115 ***
## aug.nokr -0.001512 0.055002 -0.027 0.978213
## pH -0.648601 2.942489 -0.220 0.826689
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.115 on 39 degrees of freedom
## Multiple R-squared: 0.7273, Adjusted R-squared: 0.6923
## F-statistic: 20.8 on 5 and 39 DF, p-value: 4.495e-10Secinājumi: kopējais regresijas modelis ir būtisks, jo p-vērtība ir mazāka par būtiskuma līmeni. Šis modelis spēj izskaidrot 69,23% no biomasas vērtību variēšanas. Tomēr apskatot katru no regresoriem atsevišķi, redzams, ka augsta nokrišņu daudzuma un augsnes pH koeficienti nav būtiski.
Šajā gadījumā ir iespējami vairāki risinājumi, piemēram, apstāties pie šiem rezultātiem, vai arī veidot jaunu modeli, kurā ir izņemti nebūtiskie faktori. Katrai no pieejām ir savi piekritēji un savi kritiķi. Jāatceras, ka katra koeficienta vērtība modelī ir atkarīga no pārējiem regresoriem, kas ir iekļauti šajā modelī. Šoreiz izmantosim pieeju, ka nepieciešams izveidot modeli, kurā visi koeficienti ir būtiski, tāpēc pakāpeniski ņemsim ārā nebūtiskos regresorus. Kā pirmo izslēgsim augusta nokrišņu summu, jo šim regresoram ir vislielākā p-vērtība (0,978).
mod3<-lm(biomasa~gaisma+jun.nokr+jul.nokr+pH,data=augi2)
summary(mod3)##
## Call:
## lm(formula = biomasa ~ gaisma + jun.nokr + jul.nokr + pH, data = augi2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -10.057 -3.453 -1.302 3.459 8.742
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22.84355 20.98606 1.089 0.283
## gaisma 0.36191 0.04194 8.629 1.13e-10 ***
## jun.nokr -0.22175 0.05010 -4.426 7.22e-05 ***
## jul.nokr 0.20034 0.04592 4.362 8.79e-05 ***
## pH -0.64350 2.89971 -0.222 0.826
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.05 on 40 degrees of freedom
## Multiple R-squared: 0.7273, Adjusted R-squared: 0.7
## F-statistic: 26.67 on 4 and 40 DF, p-value: 8.057e-11Secinājumi: Arī šis modelis kopumā ir statistiski būtisks, turklāt tam ir nedaudz lielāka izskaidrotā variācija (70,0%). Tomēr pH ietekme joprojām nav būtiska, tāpēc veidojam jaunu modeli.
mod4<-lm(biomasa~gaisma+jun.nokr+jul.nokr,data=augi2)
summary(mod4)##
## Call:
## lm(formula = biomasa ~ gaisma + jun.nokr + jul.nokr, data = augi2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.972 -3.318 -1.039 3.191 9.003
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 18.29813 4.51651 4.051 0.000221 ***
## gaisma 0.36229 0.04142 8.747 6.40e-11 ***
## jun.nokr -0.21996 0.04888 -4.500 5.50e-05 ***
## jul.nokr 0.20066 0.04537 4.423 7.01e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.991 on 41 degrees of freedom
## Multiple R-squared: 0.7269, Adjusted R-squared: 0.707
## F-statistic: 36.38 on 3 and 41 DF, p-value: 1.242e-11Secinājumi: pēdējā modelī visi atsevišķie koeficienti ir statistiski būtiski, kā arī būtisks ir viss modelis kopā. Izskaidrotā variācija ir 70,7%. Apskatot koeficientu vērtības, var secināt, ka gaismas daudzuma un jūlija nokrišņu daudzuma ietekme ir pozitīva, bet jūnija nokrišņu ietekme ir negatīva.
Lai salīdzinātu divus vai vairākus modeļus (ar kopīgu regresentu) savā starpā, var izmantot AIC rādītāju, ko aprēķina ar funkciju AIC(). Salīdzinot modeļus, labāks modelis ir tas, kura AIC vērtība ir mazāka. Šajā gadījumā mazākā AIC vērtība ir mod4, kurā bija iekļauti tikai trīs būtiskie regresori.
AIC(mod2,mod4)## df AIC
## mod2 7 282.1547
## mod4 5 278.2109Pārbaudot labāko modeli ar diagnosticējošiem grafikiem (10.5 attēls), varam izdarīt secinājumu, ka atlikuma vērtības atbilst normālajam sadalījumam, kā arī modelī nav ietekmīgu novērojumu.
par(mfrow=c(2,2))
plot(mod4)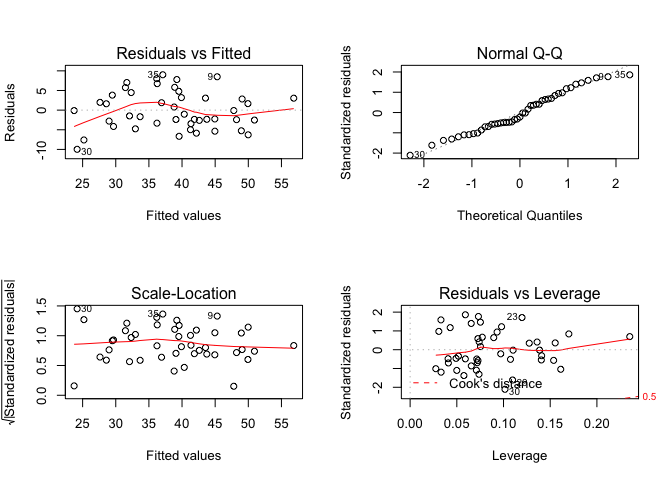
Figure 10.5: Regresijas analīzes diagnosticējošie grafiki