4 相依樣本單因子變異數分析
以R語言讀入資料並做相依樣本單因子變異數分析。
4.1 資料準備
4.1.1 讀入檔案
以xlsx套件的read.xlsx()函數或readxl套件的read_xlsx()函數來讀入上個單元中所存出的gData1.xlsx檔。
## # A tibble: 6 × 8
## 學號 性別 組別 出席 影片 期中考 期末考 總成績
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 102368014 M 9 8.5 82.6 32 28 56.0
## 2 102368018 M 10 9.5 82.9 66 59 78.8
## 3 102368024 F 9 8 82.6 69 68 81.2
## 4 102368027 F 9 8 82.6 68 83.5 86.0
## 5 102368030 F 11 0 66.5 39 30 45.2
## 6 100368033 M 4 12 73.3 58 79 82.14.1.2 準備可供變異數分析的資料
新增一假設的期初考成績,以做為變異數分析之用。
library(tibble)
gData1 <- add_column(gData1, 期初考=gData1$出席*8, .after = 5)
head(gData1)## # A tibble: 6 × 9
## 學號 性別 組別 出席 影片 期初考 期中考 期末考 總成績
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 102368014 M 9 8.5 82.6 68 32 28 56.0
## 2 102368018 M 10 9.5 82.9 76 66 59 78.8
## 3 102368024 F 9 8 82.6 64 69 68 81.2
## 4 102368027 F 9 8 82.6 64 68 83.5 86.0
## 5 102368030 F 11 0 66.5 0 39 30 45.2
## 6 100368033 M 4 12 73.3 96 58 79 82.1選擇期初考、期中考和期末考進來分析,並加入編號(亦可使用學號,這邊方便起見加入編號來做)。
gData3 <- subset(gData1, select = c(期初考, 期中考, 期末考))
gData3 <- add_column(gData3, id = c(1:nrow(gData3)), .after = 0)
head(gData3)## # A tibble: 6 × 4
## id 期初考 期中考 期末考
## <int> <dbl> <dbl> <dbl>
## 1 1 68 32 28
## 2 2 76 66 59
## 3 3 64 69 68
## 4 4 64 68 83.5
## 5 5 0 39 30
## 6 6 96 58 79用reshape2套件的melt()函數,將期初、期中、期末考合併為一行。
library(reshape2)
gData3m <- melt(gData3, id = c("id"), measured = c("期初考", "期中考", "期末考"))
head(gData3m)## id variable value
## 1 1 期初考 68
## 2 2 期初考 76
## 3 3 期初考 64
## 4 4 期初考 64
## 5 5 期初考 0
## 6 6 期初考 96更改column的名稱。
## 編號 考試 成績
## 1 1 期初考 68
## 2 2 期初考 76
## 3 3 期初考 64
## 4 4 期初考 64
## 5 5 期初考 0
## 6 6 期初考 96以上資料格式即為變異數分析所需的格式。
在執行相依樣本單因子變異數分析時,要注意的是,資料必須如此例這般,不同組的資料以「接續」的方式排列。若拿到的資料是一般相依樣本的資料輸入方式(即不同組在不同的columns),需先進行資料的處理,將wide data轉為long data,再做相依樣本單因子變異數分析。
4.2 描述統計
檢視三次考試的平均數和標準差。
| Variable | N | Mean | SD | N | Mean | SD | N | Mean | SD |
|---|---|---|---|---|---|---|---|---|---|
| 編號 | 57 | 29 | 16.598 | 57 | 29 | 16.598 | 57 | 29 | 16.598 |
| 成績 | 57 | 82.807 | 18.485 | 57 | 54.947 | 13.313 | 57 | 59.456 | 18.216 |
以boxplot來看作圖。
boxplot(成績~考試, data=gData3m)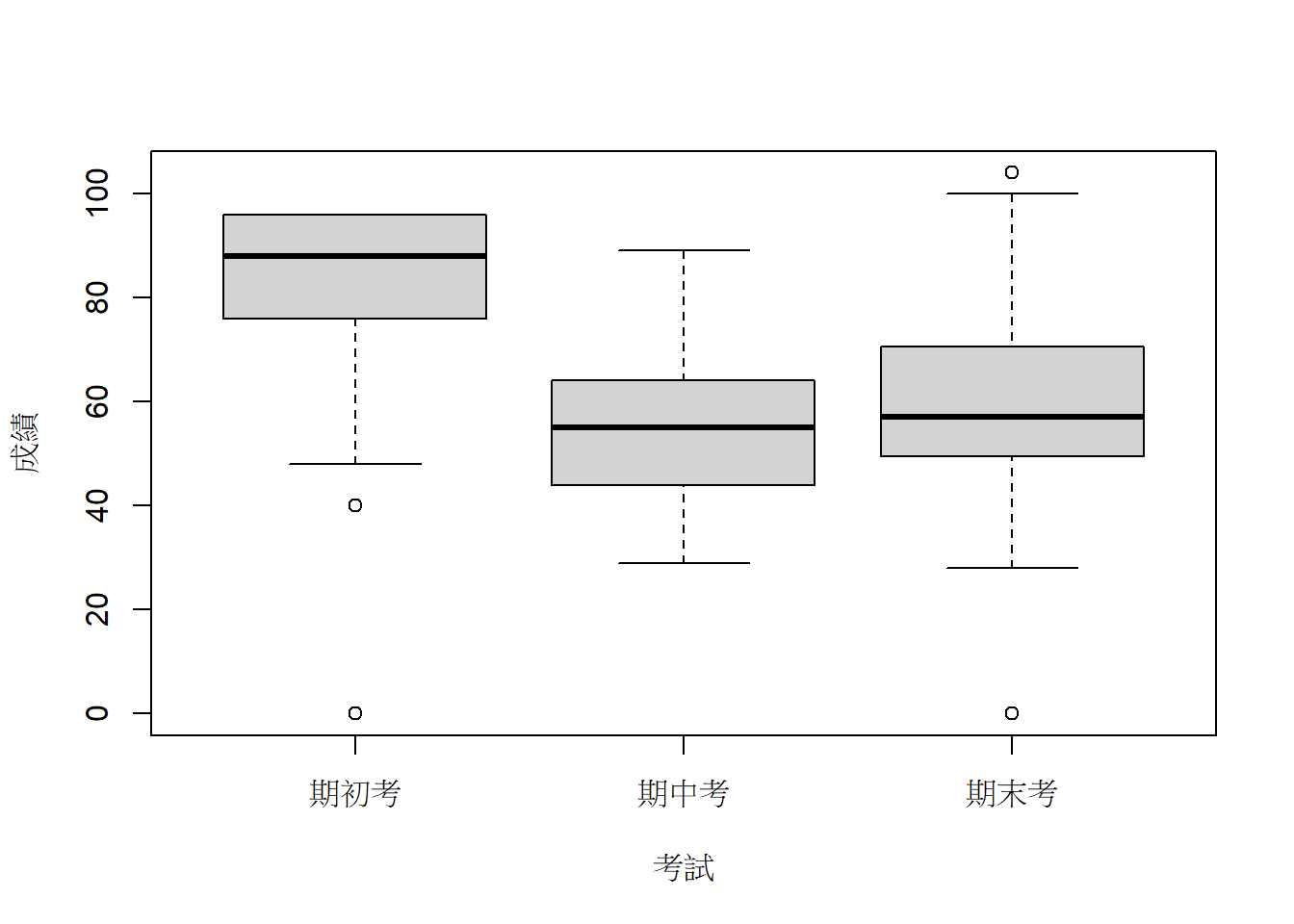
以ggpubr套件的ggline函數來作圖,畫平均數和標準差。
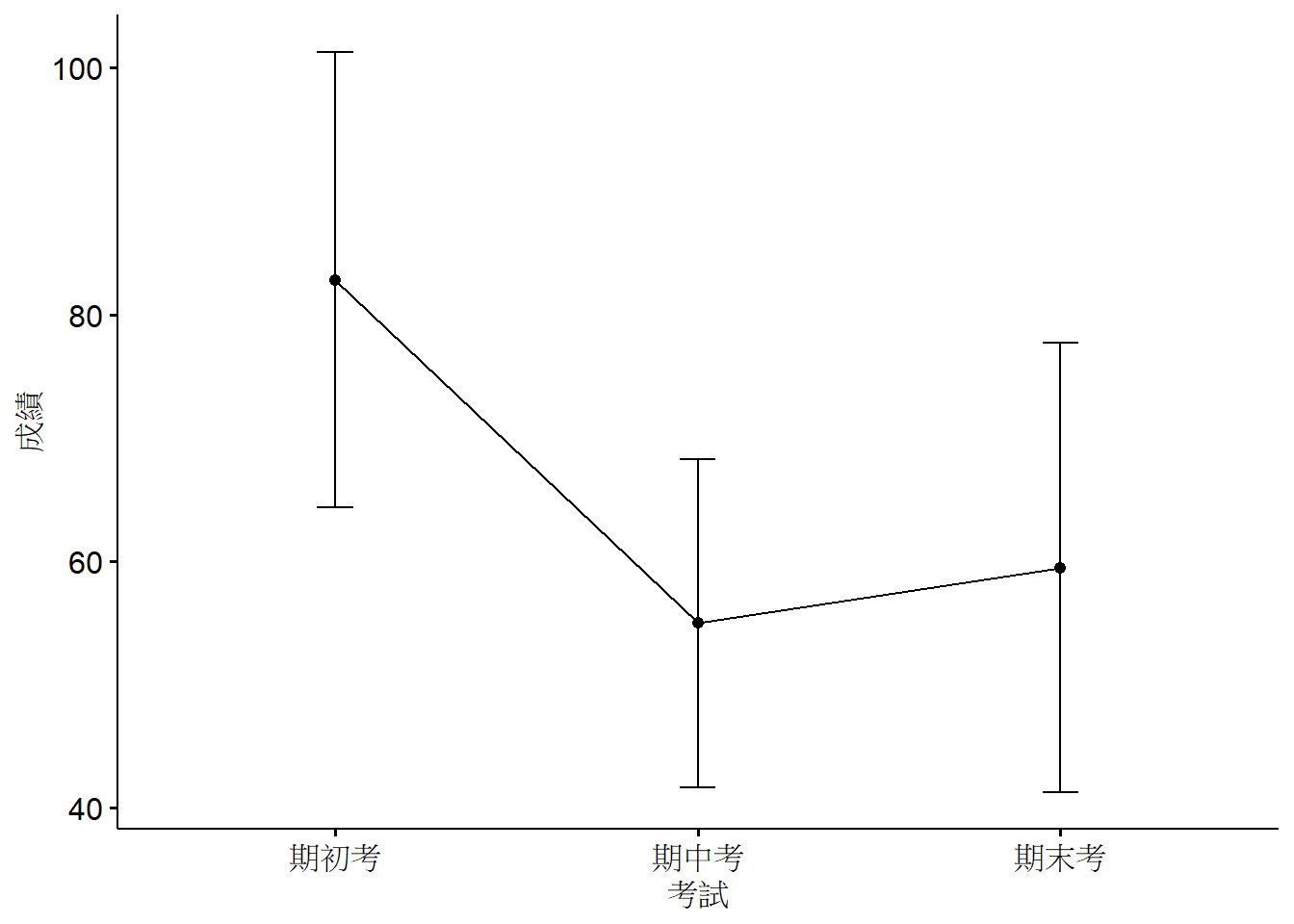
4.3 變異數分析
先將編號的格式改為factor。
## 編號 考試 成績
## 1 1 期初考 68
## 2 2 期初考 76
## 3 3 期初考 64
## 4 4 期初考 64
## 5 5 期初考 0
## 6 6 期初考 964.3.1 球型檢定與變異數分析
用rstatix package中的anova_test()來做變異數分析,將結果儲存為res。並以res來看檢驗的結果。
因本資料違反球型檢定,需要看sphericity correction的表。Sphericity Corrections以Greenhouse-Geisser (GG)和Huynh-Feldt (HF) epsilon values來做校正。校正後的值 p[GG] 和 p[HF] 皆小於.001,表示不同考試成績有顯著差異。
library(rstatix)
res <- anova_test(data = gData3m, dv = 成績, wid = 編號, within = 考試)
res## ANOVA Table (type III tests)
##
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 考試 2 112 73.704 3.74e-21 * 0.349
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 1 考試 0.84 0.008 *
##
## $`Sphericity Corrections`
## Effect GGe DF[GG] p[GG] p[GG]<.05 HFe DF[HF] p[HF]
## 1 考試 0.862 1.72, 96.57 1.4e-18 * 0.887 1.77, 99.36 4.8e-19
## p[HF]<.05
## 1 *最後,用get_anova_table()來看校正後的結果。校正的結果顯示,F(1.72, 96.57) = 73.704, p < .001。三次考試的成績顯著不同。
get_anova_table(res)## ANOVA Table (type III tests)
##
## Effect DFn DFd F p p<.05 ges
## 1 考試 1.72 96.57 73.704 1.4e-18 * 0.3494.3.2 多重比較
可用pairwise_t_test()來做兩兩比較,看差異來自於哪裡。結果顯示期中和期末考沒有差異,其餘兩兩比較都有差異。
pairwise_t_test(gData3m, 成績 ~ 考試, paired = TRUE, p.adjust.method = "bonferroni")## # A tibble: 3 × 10
## .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
## * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 成績 期初考 期中考 57 57 10.4 56 1.11e-14 3.33e-14 ****
## 2 成績 期初考 期末考 57 57 8.60 56 8.06e-12 2.42e-11 ****
## 3 成績 期中考 期末考 57 57 -2.36 56 2.2 e- 2 6.5 e- 2 ns4.3.3 若未違反球型檢定
若是球型檢定沒有違反,也可以用aov()來做變異數分析。在aov()中,以y~factor(x)+Error(factor(Subj)/factor(x))來執行變異數分析。
以model.tables()來看各組的邊緣平均數(marginal mean)和總平均數(ground mean)。總平均數為65.74,期初、期中和期末考的平均數分別為82.81、54.95與59.46。
model.tables(ANOVAData,type="means")## Tables of means
## Grand mean
##
## 65.73684
##
## factor(考試)
## factor(考試)
## 期初考 期中考 期末考
## 82.81 54.95 59.46以summary()來看ANOVA table。可得到F(2,112)=73.7,p<.001,表示三次考試的成績有顯著差異。
summary(ANOVAData,type="means")##
## Error: factor(編號)
## Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 56 28272 504.9
##
## Error: factor(編號):factor(考試)
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(考試) 2 25493 12747 73.7 <2e-16 ***
## Residuals 112 19370 173
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1