6 混合樣本二因子變異數分析
以R語言讀入資料並做混合樣本二因子變異數分析。
6.1 資料準備
6.1.1 讀入檔案
以xlsx套件的read.xlsx()函數或readxl套件的read_xlsx()函數來讀入上個單元中所存出的gData1.xlsx檔。
library(readxl)
gData1 <- read_xlsx("gData1.xlsx")
gData1 <- as.data.frame(gData1)
head(gData1)## 學號 性別 組別 出席 影片 期中考 期末考 總成績
## 1 102368014 M 9 8.5 82.58333 32 28.0 56.02778
## 2 102368018 M 10 9.5 82.93333 66 59.0 78.81111
## 3 102368024 F 9 8.0 82.58333 69 68.0 81.19444
## 4 102368027 F 9 8.0 82.58333 68 83.5 86.02778
## 5 102368030 F 11 0.0 66.53333 39 30.0 45.17778
## 6 100368033 M 4 12.0 73.33333 58 79.0 82.111116.1.2 準備可供變異數分析的資料
新增一假設的期初考成績,以做為變異數分析之用。
library(tibble)
gData1 <- add_column(gData1, 期初考=gData1$出席*8, .after = 5)
head(gData1)## 學號 性別 組別 出席 影片 期初考 期中考 期末考 總成績
## 1 102368014 M 9 8.5 82.58333 68 32 28.0 56.02778
## 2 102368018 M 10 9.5 82.93333 76 66 59.0 78.81111
## 3 102368024 F 9 8.0 82.58333 64 69 68.0 81.19444
## 4 102368027 F 9 8.0 82.58333 64 68 83.5 86.02778
## 5 102368030 F 11 0.0 66.53333 0 39 30.0 45.17778
## 6 100368033 M 4 12.0 73.33333 96 58 79.0 82.11111加入編號(亦可使用學號,這邊方便起見加入編號來做),並選擇性別、期初考、期中考和期末考進來分析。
gData2 <- add_column(gData1, 編號 = c(1:nrow(gData1)), .after = 0)
gData2WA <- subset(gData2, select = c("編號", "性別", "期初考", "期中考", "期末考"))
head(gData2WA)## 編號 性別 期初考 期中考 期末考
## 1 1 M 68 32 28.0
## 2 2 M 76 66 59.0
## 3 3 F 64 69 68.0
## 4 4 F 64 68 83.5
## 5 5 F 0 39 30.0
## 6 6 M 96 58 79.0移除gData2WA的三位女生的資料,使資料為等格。並將資料中男生的期初和期中考分數略加修改,改為有交互作用的資料。
gData2WAmi <- gData2WA[-c(5, 47, 56), ]
gData2WAmi[which(gData2WAmi$性別=='M'), c('期初考')] <- gData2WAmi[which(gData2WAmi$性別=='M'), c('期初考')]-22
gData2WAmi[which(gData2WAmi$性別=='M'), c('期中考')] <- gData2WAmi[which(gData2WAmi$性別=='M'), c('期中考')]-18
head(gData2WAmi)## 編號 性別 期初考 期中考 期末考
## 1 1 M 46 14 28.0
## 2 2 M 54 48 59.0
## 3 3 F 64 69 68.0
## 4 4 F 64 68 83.5
## 6 6 M 74 40 79.0
## 7 7 F 96 67 78.0將三次考試的資料合併為一行,並重新命名資料的欄位名稱。
##
## Attaching package: 'reshape'## The following objects are masked from 'package:plyr':
##
## rename, round_any## The following objects are masked from 'package:reshape2':
##
## colsplit, melt, recast
gData2WAmim <- melt(gData2WAmi, id = c("編號", "性別"), measured = c("期初考", "期中考", "期末考"))
names(gData2WAmim)[3:4] <- c('考試類型', '成績')
head(gData2WAmim)## 編號 性別 考試類型 成績
## 1 1 M 期初考 46
## 2 2 M 期初考 54
## 3 3 F 期初考 64
## 4 4 F 期初考 64
## 5 6 M 期初考 74
## 6 7 F 期初考 96以上資料格式即為變異數分析所需的格式。
在執行混合因子變異數分析時,要注意的是,資料必須如此例這般,不同受試者內組別的資料以「接續」的方式排列。若拿到的資料是一般的資料輸入方式(即不同受試者內的組別在不同的columns),需先進行資料的處理,將wide data轉為long data,再做混合因子變異數分析。
6.2 描述統計
檢視不同性別在三次考試的平均數和標準差。
library(rstatix)
get_summary_stats(group_by(gData2WAmim, 性別, 考試類型), 成績, type = "mean_sd")## # A tibble: 6 × 6
## 性別 考試類型 variable n mean sd
## <chr> <fct> <chr> <dbl> <dbl> <dbl>
## 1 F 期初考 成績 27 85.5 13.6
## 2 F 期中考 成績 27 54.9 12.2
## 3 F 期末考 成績 27 63.1 15.0
## 4 M 期初考 成績 27 61.4 16.1
## 5 M 期中考 成績 27 39.0 13.8
## 6 M 期末考 成績 27 59.6 17.3也可以用psych套件的describeBy()函數。
library(psych)
with(gData2WAmim, describeBy(成績,list(性別, 考試類型)))##
## Descriptive statistics by group
## : F
## : 期初考
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 27 85.48 13.64 88 87.48 11.86 40 96 56 -1.54 2.27 2.62
## ------------------------------------------------------------
## : M
## : 期初考
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 27 61.41 16.07 66 63.74 11.86 18 74 56 -1.24 0.45 3.09
## ------------------------------------------------------------
## : F
## : 期中考
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 27 54.85 12.15 55 54.61 14.83 35 85 50 0.23 -0.48 2.34
## ------------------------------------------------------------
## : M
## : 期中考
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 27 38.96 13.8 40 38.26 8.9 14 71 57 0.3 -0.27 2.66
## ------------------------------------------------------------
## : F
## : 期末考
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 27 63.09 15.04 58.5 61.91 14.08 43 104 61 0.81 -0.01 2.9
## ------------------------------------------------------------
## : M
## : 期末考
## vars n mean sd median trimmed mad min max range skew kurtosis se
## X1 1 27 59.57 17.3 59 58.76 14.83 28 100 72 0.47 -0.32 3.33以ggpubr套件的ggline函數來作圖,畫平均數和標準差。
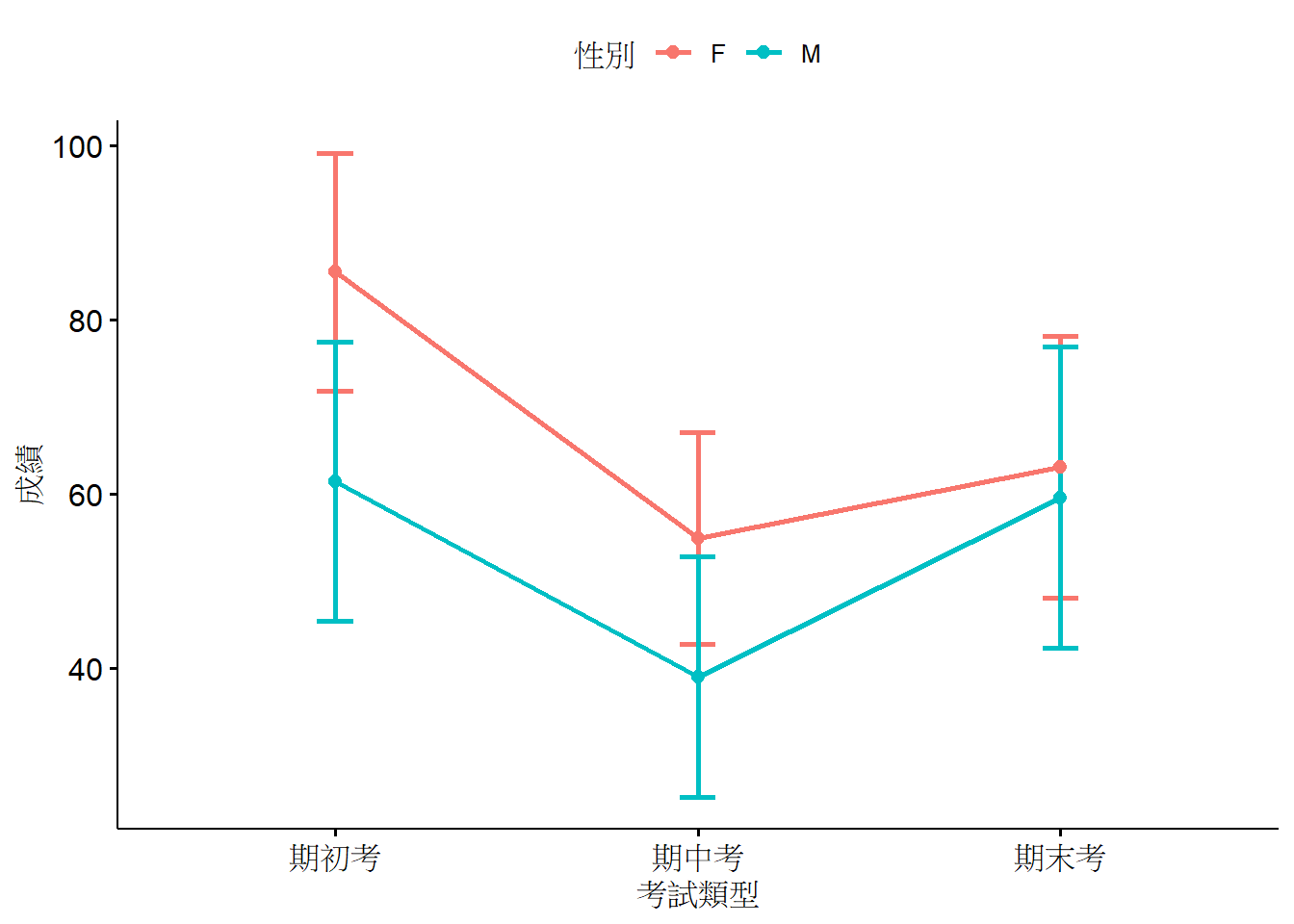
6.3 變異數分析
先將編號和性別的格式改為factor。
## 'data.frame': 162 obs. of 4 variables:
## $ 編號 : Factor w/ 54 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## $ 性別 : Factor w/ 2 levels "F","M": 2 2 1 1 2 1 1 1 2 2 ...
## $ 考試類型: Factor w/ 3 levels "期初考","期中考",..: 1 1 1 1 1 1 1 1 1 1 ...
## $ 成績 : num 46 54 64 64 74 96 40 96 74 66 ...用levene_test()做變異數同質性檢定。預設值是center=median,如有需要可改為center=mean。分析結果可知,無論是何種考試類型,成績在不同性別上都不違反變異數同質性假設。
levene_test(group_by(gData2WAmim, 考試類型), 成績 ~ 性別)## # A tibble: 3 × 5
## 考試類型 df1 df2 statistic p
## <fct> <int> <int> <dbl> <dbl>
## 1 期初考 1 52 0.239 0.627
## 2 期中考 1 52 0.156 0.695
## 3 期末考 1 52 0.273 0.604用rstatix package中的anova_test()來做球型檢定和變異數分析,將結果儲存為res.aov。並以res.aov來看檢驗的結果。
因本資料違反球型假設,需要看sphericity correction的表。Sphericity Corrections以Greenhouse-Geisser (GG)和Huynh-Feldt (HF) epsilon values來做校正。校正後的值 p[GG] 和 p[HF] 皆小於.001,表示不同考試類型的成績有顯著差異,且存在性別與考試類型的交互作用。
library(rstatix)
res.aov <- anova_test(data = gData2WAmim, dv = 成績, wid = 編號, between = 性別, within = 考試類型)
res.aov## ANOVA Table (type II tests)
##
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 性別 1 52 22.604 1.62e-05 * 0.200
## 2 考試類型 2 104 68.691 9.66e-20 * 0.359
## 3 性別:考試類型 2 104 10.420 7.51e-05 * 0.078
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 1 考試類型 0.817 0.006 *
## 2 性別:考試類型 0.817 0.006 *
##
## $`Sphericity Corrections`
## Effect GGe DF[GG] p[GG] p[GG]<.05 HFe DF[HF] p[HF]
## 1 考試類型 0.846 1.69, 87.94 4.53e-17 * 0.871 1.74, 90.57 1.65e-17
## 2 性別:考試類型 0.846 1.69, 87.94 2.11e-04 * 0.871 1.74, 90.57 1.78e-04
## p[HF]<.05
## 1 *
## 2 *最後,用get_anova_table()來看校正後的結果。校正的結果顯示,性別主效果顯著,F(1, 52) = 22.6, p < .001;考試類型主效果顯著,F(1.69, 87.94) = 68.7, p < .001;兩變項的交互作用顯著,F(1.69, 87.94) = 10.4, p < .001。
get_anova_table(res.aov)## ANOVA Table (type II tests)
##
## Effect DFn DFd F p p<.05 ges
## 1 性別 1.00 52.00 22.604 1.62e-05 * 0.200
## 2 考試類型 1.69 87.94 68.691 4.53e-17 * 0.359
## 3 性別:考試類型 1.69 87.94 10.420 2.11e-04 * 0.0786.3.1 事後比較
交互作用顯著時的單純主要效果檢驗 因交互作用顯著,故需分析單純主要效果。先依考試類型來分組,看性別的主要效果。可知男女在期初考和期考成績有差異,在期末考則無。adjust_pvalue()會考慮alpha值膨脹的問題,在控制三個檢定的alpha值不超過.05來計算p value。
anova1 <- anova_test(group_by(gData2WAmim, 考試類型), dv=成績, wid=編號, between=性別)
adjust_pvalue(get_anova_table(anova1), method="bonferroni")## # A tibble: 3 × 9
## 考試類型 Effect DFn DFd F p `p<.05` ges p.adj
## <fct> <chr> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl>
## 1 期初考 性別 1 52 35.2 0.000000243 "*" 0.404 0.000000729
## 2 期中考 性別 1 52 20.2 0.0000398 "*" 0.279 0.000119
## 3 期末考 性別 1 52 0.636 0.429 "" 0.012 1依性別來分組,看考試類型的主要效果。可知考試類型在男女上皆有差異。
anova2 <- anova_test(group_by(gData2WAmim, 性別), dv=成績, wid=編號, within=考試類型)
adjust_pvalue(get_anova_table(anova2), method = "bonferroni")## # A tibble: 2 × 9
## 性別 Effect DFn DFd F p `p<.05` ges p.adj
## <fct> <chr> <dbl> <dbl> <dbl> <dbl> <chr> <dbl> <dbl>
## 1 F 考試類型 2 52 43.6 7.63e-12 * 0.482 1.53e-11
## 2 M 考試類型 2 52 34.4 3.03e-10 * 0.301 6.06e-10進一步以兩兩比較去看兩個主效果的差異在哪裡。結果顯示,女生無論是期初vs.期中、期初vs.期末、期vs.期末都有差異;男生則只有期初vs.期中、期中vs.期末有差異。
pairwise_t_test(group_by(gData2WAmim,性別), 成績 ~ 考試類型, paired = TRUE, p.adjust.method = "bonferroni")## # A tibble: 6 × 11
## 性別 .y. group1 group2 n1 n2 statistic df p p.adj
## * <fct> <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl>
## 1 F 成績 期初考 期中考 27 27 8.73 26 0.00000000334 1 e-8
## 2 F 成績 期初考 期末考 27 27 5.72 26 0.00000506 1.52e-5
## 3 F 成績 期中考 期末考 27 27 -3.13 26 0.004 1.3 e-2
## 4 M 成績 期初考 期中考 27 27 6.67 26 0.000000447 1.34e-6
## 5 M 成績 期初考 期末考 27 27 0.557 26 0.582 1 e+0
## 6 M 成績 期中考 期末考 27 27 -9.27 26 0.000000001 3 e-9
## # … with 1 more variable: p.adj.signif <chr>6.3.2 交互作用未顯著時的事後比較
若交互作用未顯著,看主效果的事後比較。因性別只有兩個levels,不需進行事後比較。因此看考試類型的兩兩比較,結果顯示,三種考試的成績兩兩之間都有差異。
pairwise_t_test(gData2WAmim, 成績~考試類型, paired = TRUE, p.adjust.method = "bonferroni")## # A tibble: 3 × 10
## .y. group1 group2 n1 n2 statistic df p p.adj p.adj.signif
## * <chr> <chr> <chr> <int> <int> <dbl> <dbl> <dbl> <dbl> <chr>
## 1 成績 期初考 期中考 54 54 10.7 53 6.73e-15 2.02e-14 ****
## 2 成績 期初考 期末考 54 54 4.18 53 1.1 e- 4 3.3 e- 4 ***
## 3 成績 期中考 期末考 54 54 -7.56 53 5.6 e-10 1.68e- 9 ****