Chapter 8 調節與中介
本單元介紹如何以R語言做調節與中介分析。
8.1 讀入資料
setwd("D:\\Dropbox\\Working\\教師社群")cData <- read.table("moderation.csv", header=TRUE, sep=",")8.2 調節變項為類別變項
將affection中心化的結果：可知兩模型皆顯著。加入交互作用的模型比未加入的模型可以多解釋9%的變異量，此增加的解釋量達到顯著，diff R^2 = .09, F(1,96) = 64.1, p < .001。迴歸式為closeness = 6.36873 + 0.41746 affection - 4.42985 * genderM - 0.37521 * affection * genderM。
library(pequod)## Warning: 套件 'pequod' 是用 R 版本 4.1.3 來建造的## 載入需要的套件：ggplot2## 載入需要的套件：car## 載入需要的套件：carDatam1 <- lmres(closeness~affection*gender, centered=c("affection"), data=cData)
summary(m1, type="nested")## **Models**
##
## Model 1: closeness ~ affection + genderMale
## <environment: 0x0000000015e8e688>
##
## Model 2: closeness ~ affection + genderMale + affection.XX.genderMale
## <environment: 0x0000000015e8e688>
##
##
## **Statistics**
##
## R R^2 Adj. R^2 Diff.R^2 F df1 df2 p.value
## Model 1 0.88 0.77 0.76 0.77 160.04 2.00 97 < 2.2e-16 ***
## Model 2: 0.93 0.86 0.86 0.09 197.52 3.00 96 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## **F change**
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 97 177
## 2 96 106 1 71 64.1 2.7e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## **Coefficients**
##
## Estimate StdErr t.value beta p.value
## -- Model 1 --
##
## (Intercept) 6.29135 0.19168 32.82144 < 2.2e-16 ***
## affection 0.26269 0.02963 8.86462 0.4367 < 2.2e-16 ***
## genderMale -4.46269 0.27189 -16.41354 -0.8085 < 2.2e-16 ***
##
##
## -- Model 2 --
##
## (Intercept) 6.36873 0.14950 42.60126 < 2.2e-16 ***
## affection 0.41746 0.03009 13.87403 0.6939 < 2.2e-16 ***
## genderMale -4.42985 0.21165 -20.93042 -0.8026 < 2.2e-16 ***
## affection.XX.genderMale -0.37521 0.04685 -8.00877 -0.3996 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Simple slope分析。可以看gender和affection在正負一個標準差時的預測值。
Sim_m1 <- simpleSlope(m1, pred="affection", mod1="genderMale", coded="genderMale")
summary(Sim_m1)##
## ** Estimated points of closeness **
##
## Low affection (-1 SD) High affection (+1 SD)
## Low genderMale ( 0 ) 4.4440 8.2935
## High genderMale ( 1 ) 1.7441 2.1337
##
##
##
## ** Simple Slopes analysis ( df= 96 ) **
##
## simple slope standard error t-value p.value
## Low genderMale ( 0 ) 0.4175 0.0301 13.87 <2e-16 ***
## High genderMale ( 1 ) 0.0422 0.0359 1.18 0.24
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
##
## ** Bauer & Curran 95% CI **
##
## lower CI upper CI
## genderMale 0.9366 1.3778Simple Slope作圖。可畫出調節變項在正負一個標準差時的圖。
PlotSlope(Sim_m1)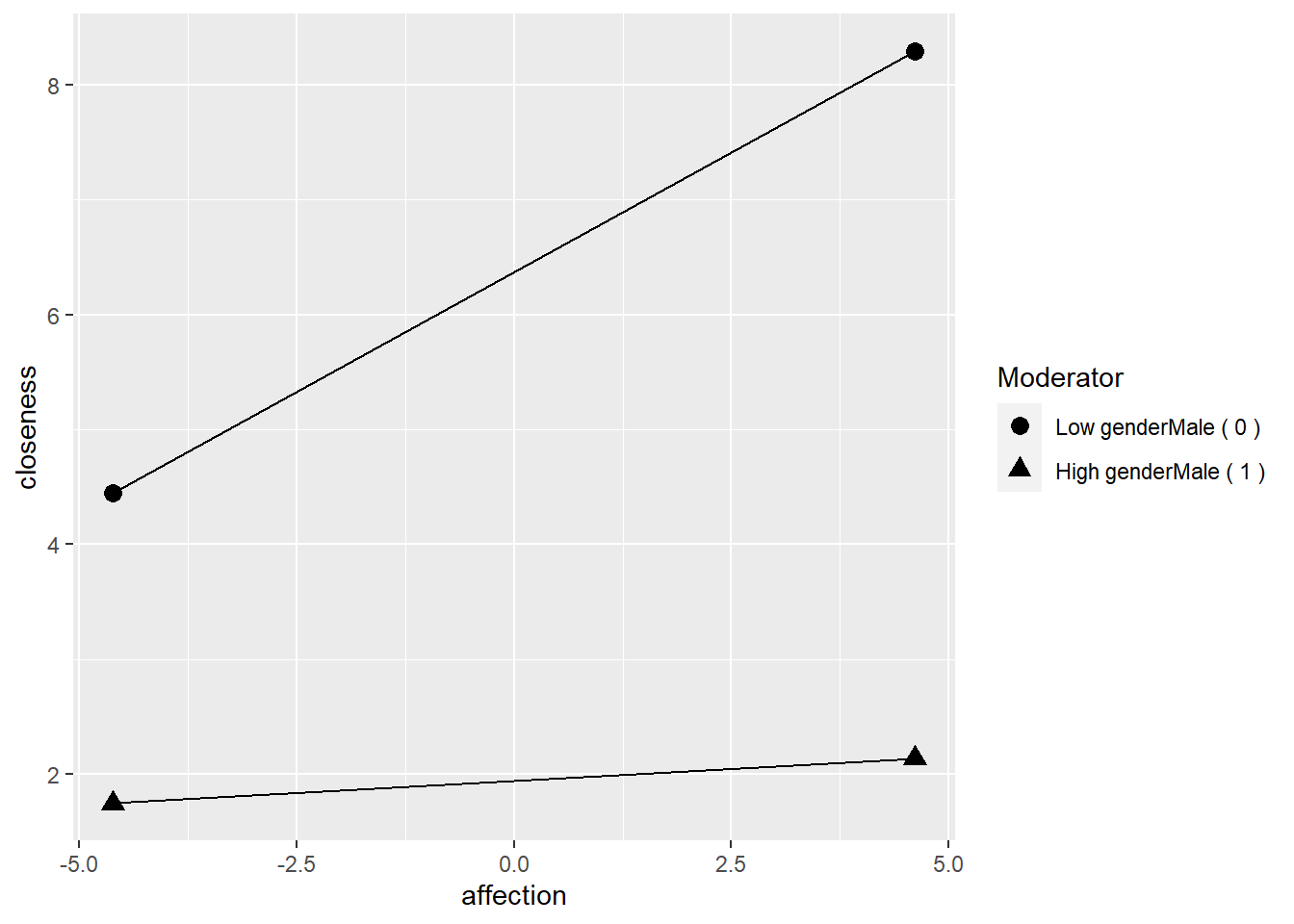
8.3 調節變項為連續變項
模型與上面相同。
library(pequod)
m2 <- lmres(closeness~gender*affection, centered=c("affection"), data=cData)
summary(m2, type="nested")## **Models**
##
## Model 1: closeness ~ genderMale + affection
## <environment: 0x0000000022785550>
##
## Model 2: closeness ~ genderMale + affection + genderMale.XX.affection
## <environment: 0x0000000022785550>
##
##
## **Statistics**
##
## R R^2 Adj. R^2 Diff.R^2 F df1 df2 p.value
## Model 1 0.88 0.77 0.76 0.77 160.04 2.00 97 < 2.2e-16 ***
## Model 2: 0.93 0.86 0.86 0.09 197.52 3.00 96 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## **F change**
##
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 97 177
## 2 96 106 1 71 64.1 2.7e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
## **Coefficients**
##
## Estimate StdErr t.value beta p.value
## -- Model 1 --
##
## (Intercept) 6.29135 0.19168 32.82144 < 2.2e-16 ***
## genderMale -4.46269 0.27189 -16.41354 -0.8085 < 2.2e-16 ***
## affection 0.26269 0.02963 8.86462 0.4367 < 2.2e-16 ***
##
##
## -- Model 2 --
##
## (Intercept) 6.36873 0.14950 42.60126 < 2.2e-16 ***
## genderMale -4.42985 0.21165 -20.93042 -0.8026 < 2.2e-16 ***
## affection 0.41746 0.03009 13.87403 0.6939 < 2.2e-16 ***
## genderMale.XX.affection -0.37521 0.04685 -8.00877 -0.3996 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1同樣做simple slope分析。
Sim_m2 <- simpleSlope(m1, pred="genderMale", mod1="affection")
summary(Sim_m2)##
## ** Estimated points of closeness **
##
## Low genderMale (-1 SD) High genderMale (+1 SD)
## Low affection (-1 SD) 4.4508 1.7373
## High affection (+1 SD) 8.3090 2.1182
##
##
##
## ** Simple Slopes analysis ( df= 96 ) **
##
## simple slope standard error t-value p.value
## Low affection (-1 SD) -2.700 0.305 -8.84 <2e-16 ***
## High affection (+1 SD) -6.160 0.300 -20.57 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
##
##
## ** Bauer & Curran 95% CI **
##
## lower CI upper CI
## affection -15.864 -9.2647PlotSlope(Sim_m2)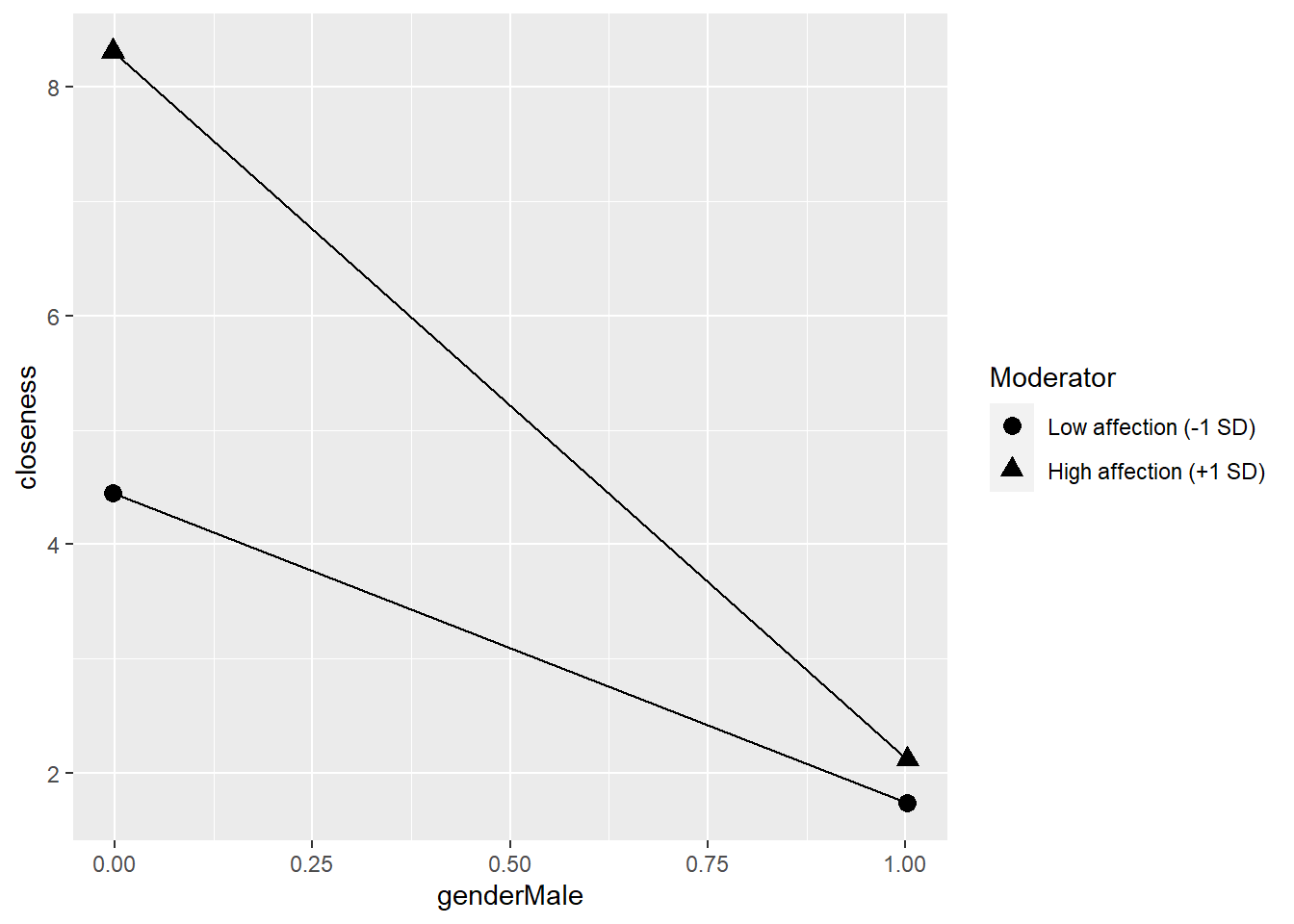
另一種作法。
cData$affectionC <- c(scale(cData$affection, center=TRUE, scale=FALSE))res0 <- lm(closeness ~ affectionC + gender, data=cData)
summary(res0)##
## Call:
## lm(formula = closeness ~ affectionC + gender, data = cData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.3733 -0.8598 0.2029 0.8282 3.0625
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.29135 0.19168 32.821 < 2e-16 ***
## affectionC 0.26269 0.02963 8.865 3.78e-14 ***
## genderMale -4.46269 0.27189 -16.414 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.351 on 97 degrees of freedom
## Multiple R-squared: 0.7674, Adjusted R-squared: 0.7626
## F-statistic: 160 on 2 and 97 DF, p-value: < 2.2e-16res1 <- lm(closeness ~ affectionC + gender + affectionC*gender, data=cData)
summary(res1)##
## Call:
## lm(formula = closeness ~ affectionC + gender + affectionC * gender,
## data = cData)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.18730 -0.74369 -0.06341 0.68137 2.89720
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.36873 0.14950 42.601 < 2e-16 ***
## affectionC 0.41746 0.03009 13.874 < 2e-16 ***
## genderMale -4.42985 0.21165 -20.930 < 2e-16 ***
## affectionC:genderMale -0.37521 0.04685 -8.009 2.72e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.052 on 96 degrees of freedom
## Multiple R-squared: 0.8606, Adjusted R-squared: 0.8562
## F-statistic: 197.5 on 3 and 96 DF, p-value: < 2.2e-16anova(res0, res1)## Analysis of Variance Table
##
## Model 1: closeness ~ affectionC + gender
## Model 2: closeness ~ affectionC + gender + affectionC * gender
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 97 177.14
## 2 96 106.19 1 70.948 64.14 2.722e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1library(processR)## Registered S3 methods overwritten by 'broom':
## method from
## tidy.glht jtools
## tidy.summary.glht jtools##
## 載入套件：'processR'## 下列物件被遮斷自 'package:car':
##
## densityPlot, qqPlotmodelsSummary(res1)## ===============================================================
## Consequent
## --------------------------------------
## closeness
## -------------------------------------
## Antecedent Coef SE t p
## ---------------------------------------------------------------
## affectionC b1 0.417 0.030 13.874 <.001
## genderMale b2 -4.430 0.212 -20.930 <.001
## affectionC:genderMale b3 -0.375 0.047 -8.009 <.001
## Constant iy 6.369 0.149 42.601 <.001
## ---------------------------------------------------------------
## Observations 100
## R2 0.861
## Adjusted R2 0.856
## Residual SE 1.052 ( df = 96)
## F statistic F(3,96) = 197.519, p < .001
## ===============================================================