Chapter 10 Jul 17–23: Regression and classification with KNN, Decision Trees, and Random Forest
10.1 Goals and introduction
This week, our goals are to…
- Use selected regression and classification techniques to make predictions.
In this chapter, we will use supervised machine learning techniques—KNN, decision trees, and random forest—to make predictions on both continuous and categorical outcomes (dependent variables). When we have a continuous numeric outcome, we will use regression techniques to make predictions. When we have a categorical outcome, we will use classification techniques. Methods like the ones we will use in this chapter can be used for both regression and classification; it all just depends on the outcome of interest (numeric or categorical).
The following tutorial in this chapter shows how to import, split (into training and testing), and create a model with your data. Then, we will look at how to use the models to make predictions and measure how good or bad the models are at making predictions for us.
10.2 Regression and classification
This section contains some optional information about the differences between regression and classification.
10.2.1 Comparison
What is the difference between regression and classification?
Regression refers to a predictive model that predicts a numeric variable. For example, if you want to predict a student’s test score or how many grams of ice cream a person eats each day, you will need to use regression.
Classification refers to a predictive model that predicts a categorical variable. For example, if you want to predict whether a student will be admitted or not to an educational program or a person’s favorite ice cream flavor, you will need to use classification.
Both regression and classification are supervised machine learning methods.
This reference table further points out differences and similarities:
| Type of model | Dependent variable | Dependent variable examples | Methods examples |
|---|---|---|---|
| regression | numeric | test scores, blood pressure, stock prices, how fast somebody can run a mile, how many potatoes somebody will purchase at the store | linear regression, k-nearest neighbors regression, random forest regression, neural network regression, many others |
| classification | categorical | favorite ice cream flavor, whether or not somebody has diabetes (yes or no), admissions decision (yes or no), whether or not someone buys a product (yes or no), political party. | logistic regression39, k-nearest neighbors classification, random forest classification, neural network classification, many others |
- Note that many types of machine learning work for both regression and classification (such as KNN and random forest).
10.3 Import and prepare data
As always, we have to begin by preparing our data before we can use it for analysis. This procedure is one that you will already be familiar with.
For the examples in this tutorial, I will again just use the mtcars dataset that is already built into R.
Like before, we will “import” this and give it a new name—df—so that it is easier to type.
df <- mtcarsRun the following command in your own R console40 to see information about the data, if you want:
?mtcarsSee all variable names:
names(df)## [1] "mpg" "cyl" "disp" "hp" "drat"
## [6] "wt" "qsec" "vs" "am" "gear"
## [11] "carb"Number of observations:
nrow(df)## [1] 32Remove missing observations, if necessary:
df <- na.omit(df)Inspect some rows in the dataset:
head(df)## mpg cyl disp hp drat
## Mazda RX4 21.0 6 160 110 3.90
## Mazda RX4 Wag 21.0 6 160 110 3.90
## Datsun 710 22.8 4 108 93 3.85
## Hornet 4 Drive 21.4 6 258 110 3.08
## Hornet Sportabout 18.7 8 360 175 3.15
## Valiant 18.1 6 225 105 2.76
## wt qsec vs am gear
## Mazda RX4 2.620 16.46 0 1 4
## Mazda RX4 Wag 2.875 17.02 0 1 4
## Datsun 710 2.320 18.61 1 1 4
## Hornet 4 Drive 3.215 19.44 1 0 3
## Hornet Sportabout 3.440 17.02 0 0 3
## Valiant 3.460 20.22 1 0 3
## carb
## Mazda RX4 4
## Mazda RX4 Wag 4
## Datsun 710 1
## Hornet 4 Drive 1
## Hornet Sportabout 2
## Valiant 1Make a backup copy of our data:
dfcopy <- dfConvert non-numeric variables to dummy (binary) variables, if necessary:
if (!require(fastDummies)) install.packages('fastDummies')
library(fastDummies)
df <- dummy_cols(df, remove_first_dummy = TRUE, remove_selected_columns = TRUE)Note that the step above is only necessary when you have one or more categorical variables (called factor variables in R) in your data.
Scale the data:
df <- as.data.frame(scale(df)) # rescale all variablesAbove, we re-scaled all of the variables in the data. But that means that we also re-scaled the dependent variable, mpg, which we didn’t need to do. I like to keep the dependent variable in its original, unscaled form so that it is easier to interpret later on.
Below, we remove mpg from our data:
df$mpg <- NULL ## remove scaled mpg variableAnd then we add it back into df from the copy that we saved earlier, in its original, unscaled form. This step isn’t essential but I find that it simplifies things later on (so that we can interpret the results in the original—rather than scaled—units of the dependent variable):
df$mpg <- dfcopy$mpgNow let’s inspect our data:
head(df)## cyl disp
## Mazda RX4 -0.1049878 -0.57061982
## Mazda RX4 Wag -0.1049878 -0.57061982
## Datsun 710 -1.2248578 -0.99018209
## Hornet 4 Drive -0.1049878 0.22009369
## Hornet Sportabout 1.0148821 1.04308123
## Valiant -0.1049878 -0.04616698
## hp drat
## Mazda RX4 -0.5350928 0.5675137
## Mazda RX4 Wag -0.5350928 0.5675137
## Datsun 710 -0.7830405 0.4739996
## Hornet 4 Drive -0.5350928 -0.9661175
## Hornet Sportabout 0.4129422 -0.8351978
## Valiant -0.6080186 -1.5646078
## wt qsec
## Mazda RX4 -0.610399567 -0.7771651
## Mazda RX4 Wag -0.349785269 -0.4637808
## Datsun 710 -0.917004624 0.4260068
## Hornet 4 Drive -0.002299538 0.8904872
## Hornet Sportabout 0.227654255 -0.4637808
## Valiant 0.248094592 1.3269868
## vs am
## Mazda RX4 -0.8680278 1.1899014
## Mazda RX4 Wag -0.8680278 1.1899014
## Datsun 710 1.1160357 1.1899014
## Hornet 4 Drive 1.1160357 -0.8141431
## Hornet Sportabout -0.8680278 -0.8141431
## Valiant 1.1160357 -0.8141431
## gear carb
## Mazda RX4 0.4235542 0.7352031
## Mazda RX4 Wag 0.4235542 0.7352031
## Datsun 710 0.4235542 -1.1221521
## Hornet 4 Drive -0.9318192 -1.1221521
## Hornet Sportabout -0.9318192 -0.5030337
## Valiant -0.9318192 -1.1221521
## mpg
## Mazda RX4 21.0
## Mazda RX4 Wag 21.0
## Datsun 710 22.8
## Hornet 4 Drive 21.4
## Hornet Sportabout 18.7
## Valiant 18.1All of the variables except for mpg are scaled, while mpg still has its original values.
If we wanted to, we could also completely remove some variables from the dataset. Here’s how we would remove the variables hp and wt:
df$hp <- NULL
df$wt <- NULLAnother way to remove variables uses the dplyr package. Here, we’ll include only the variables cyl, disp, wt, qsec, and mpg:
if (!require(dplyr)) install.packages('dplyr')
library(dplyr)
df <- df %>% select(cyl,disp,wt,qsec,mpg)Above, all of the other variables—the ones not included in parentheses—will be removed and the ones that are listed in parentheses will be kept.
Below, we demonstrate the opposite process, where there is a - symbol in front of certain variables. Those variables will be removed. Below, we remove hp and wt:
if (!require(dplyr)) install.packages('dplyr')
library(dplyr)
df <- df %>% select(-hp,-wt)Note that the variable inclusion/exclusion examples above were just illustrative. In this tutorial, we will not actually remove any variables. But you may want to do so when you do the homework assignment, which is why it is demonstrated above.
Now that our data is prepared, we are ready to divide our data into training and testing data sets.
10.4 Divide data
As always, we will divide our data into a training dataset that we can use to train a predictive model and then a testing dataset that we can use to determine if our predictive model is useful or not.
Below, you’ll find the code we use to split up our data. For now, I have decided to use 75% of the data to train and 25% of the data to test.
Here’s the first line of code to start the splitting process:
trainingRowIndex <- sample(1:nrow(df), 0.75*nrow(df)) # row indices for training dataNext, we assign the randomly selected observations (75% of our observations) to the training dataset:
dtrain <- df[trainingRowIndex, ] # model training dataFinally, we put all other observations (25% of our observations) into the testing dataset to use later.
dtest <- df[-trainingRowIndex, ] ## test dataNote that I did a little behind-the-scenes coding to make our testing-training split identical to that in the chapter on regression methods, so that we can easily compare the results of this new analysis with that analysis. It is not necessary for you to do the same.
We can verify if our data-splitting procedure worked:
nrow(dtrain)## [1] 24nrow(dtest)## [1] 8Above, we see that the training data contains 24 observations and the testing data contains 8 observations.
You can also look at these two datasets by running the following commands—one at a time—in your console (not your RMarkdown or R code file):
View(dtrain)
View(dtest)10.5 Regression techniques to make predictions
In this section of the tutorial, we will use three different regression techniques: k-nearest neighbors (KNN), regression trees (a decision tree used for regression), and random forest. Regression means that the dependent variable is a numeric variable.
Our goal in this portion of the tutorial is to predict each car’s mpg as accurately as possible.
10.5.1 k-Nearest neighbors regression
We are now ready to make our first predictive model, a KNN regression model. This uses the nearest neighbors procedure that we have already reviewed in class.
First, just for KNN, we have to split the data further.41 Earlier, we created training and testing datasets. Now, within each of those datasets, we have to separate the independent variables and dependent variable into separate datasets. Let’s start with the training data:
if (!require(dplyr)) install.packages('dplyr')
library(dplyr)
dtrain.x <- dtrain %>% select(-mpg) # remove mpg
dtrain.y <- dtrain %>% select(mpg) # keep only mpgAbove, we created a new dataset called dtrain.x that contains all of the independent variables from the training dataset. To create that new dataset, we looked within the old dtrain dataset and removed the variable mpg (the dependent variable). That left behind all of the independent variables in dtrain.x.
Then, in the next line, we created dtrain.y which contains only the dependent variable (mpg). To create that new dataset, we took the old dtrain dataset and selected only mpg for inclusion in dtrain.y.
Now, we’ll do this again with the testing data:
dtest.x <- dtest %>% select(-mpg) # remove mpg
dtest.y <- dtest %>% select(mpg) # keep only mpgAnd now we’ll inspect the first few rows of our four new datasets, just to be clear about what we did:
head(dtrain.x)## cyl disp
## Merc 280 -0.2357706 -0.5638586
## AMC Javelin 0.8959283 0.5129397
## Mazda RX4 Wag -0.2357706 -0.6238562
## Toyota Corolla -1.3674695 -1.3256698
## Datsun 710 -1.3674695 -1.0343658
## Maserati Bora 0.8959283 0.4892564
## hp drat
## Merc 280 -0.4177053 0.59197680
## AMC Javelin -0.0428119 -0.76027676
## Mazda RX4 Wag -0.5982095 0.55685333
## Toyota Corolla -1.2230318 1.11882884
## Datsun 710 -0.8342535 0.46904466
## Maserati Bora 2.5259020 -0.07536911
## wt qsec
## Merc 280 0.1552003 0.5275958
## AMC Javelin 0.1505536 -0.1158137
## Mazda RX4 Wag -0.3698786 -0.2959684
## Toyota Corolla -1.3363954 1.5570511
## Datsun 710 -0.8856640 0.7270528
## Maserati Bora 0.2760149 -1.8530194
## vs am
## Merc 280 1.3844373 -0.9004984
## AMC Javelin -0.6922187 -0.9004984
## Mazda RX4 Wag -0.6922187 1.0642254
## Toyota Corolla 1.3844373 1.0642254
## Datsun 710 1.3844373 1.0642254
## Maserati Bora -0.6922187 1.0642254
## gear carb
## Merc 280 0.3148618 0.5702471
## AMC Javelin -0.9445853 -0.6198338
## Mazda RX4 Wag 0.3148618 0.5702471
## Toyota Corolla 0.3148618 -1.2148742
## Datsun 710 0.3148618 -1.2148742
## Maserati Bora 1.5743088 2.9504088head(dtrain.y)## mpg
## Merc 280 19.2
## AMC Javelin 15.2
## Mazda RX4 Wag 21.0
## Toyota Corolla 33.9
## Datsun 710 22.8
## Maserati Bora 15.0head(dtest.x)## cyl disp
## Hornet 4 Drive 0.2820380 0.4355138
## Duster 360 1.4101902 1.2867217
## Merc 230 -0.8461141 -0.5425407
## Merc 280C 0.2820380 -0.3188900
## Toyota Corona -0.8461141 -0.7152858
## Pontiac Firebird 1.4101902 1.6205287
## hp drat
## Hornet 4 Drive -0.30867099 -1.2524589
## Duster 360 2.07250519 -0.9604057
## Merc 230 -0.57324612 0.6346541
## Merc 280C -0.07937254 0.6346541
## Toyota Corona -0.53796943 0.1404102
## Pontiac Firebird 0.83782125 -1.2524589
## wt qsec
## Hornet 4 Drive 0.2632441 0.23282431
## Duster 360 0.8296179 -1.49535614
## Merc 230 0.1595419 1.89379774
## Merc 280C 0.6222134 -0.02640276
## Toyota Corona -0.9333202 0.50645288
## Pontiac Firebird 1.2683582 -0.91449549
## vs am
## Hornet 4 Drive 0.5400617 -0.5400617
## Duster 360 -1.6201852 -0.5400617
## Merc 230 0.5400617 -0.5400617
## Merc 280C 0.5400617 -0.5400617
## Toyota Corona 0.5400617 -0.5400617
## Pontiac Firebird -1.6201852 -0.5400617
## gear carb
## Hornet 4 Drive -0.9354143 -0.9025825
## Duster 360 -0.9354143 1.5043042
## Merc 230 0.9354143 -0.1002869
## Merc 280C 0.9354143 1.5043042
## Toyota Corona -0.9354143 -0.9025825
## Pontiac Firebird -0.9354143 -0.1002869head(dtest.y)## mpg
## Hornet 4 Drive 21.4
## Duster 360 14.3
## Merc 230 22.8
## Merc 280C 17.8
## Toyota Corona 21.5
## Pontiac Firebird 19.2Another task we need to do before we train the model is to choose the value for k in k-nearest neighbors. k is the number of other observations in the data that will be used to make a prediction about the new data. In general, you should try different values of k in the algorithm to see what makes the best predictions.
One way to determine a value for k is to set k as the square root of the number of observations in the training data. Let’s calculate this value:
sqrt(nrow(dtrain.x))## [1] 4.898979Above, we used the nrow command to figure out the number of observations that are in the training data, which is called dtrain.x. Then, we used the sqrt command to calculate the square root of this number of observations. The answer in this case is closest to the integer 5, so I am going to choose 5 as the value of k.
Finally, it is time to train the KNN model:
if (!require(FNN)) install.packages('FNN')
library(FNN)
pred.a <- FNN::knn.reg(dtrain.x, dtest.x, dtrain.y, k = 5)Above, here’s what we did:
pred.a– We are going to compute a KNN result and we will store it aspred.a.<-– This means that we are assigning the result from the rest of the code topred.a.FNN::knn.reg– This is the functionknn.regfrom the packageFNN. This function trains the KNN model for us.dtrain.x– This is the first argument of theknn.regfunction. This is the dataset containing the independent variables for the training data.dtest.x– This is the second argument of theknn.regfunction. This is the dataset containing the independent variables for the testing data.dtrain.y– This is the third argument of theknn.regfunction. This is the dataset containing the dependent variable for the training data.k = 5– This is the fourth and final argument that I have put into theknn.regfunction. This is the number of neighbors (the value of k) that we decided earlier.
Once the knn.reg command ran, it saved the predictions made on the dtest.x data as pred.a. Let’s learn more about pred.a by checking what class of object it is:
class(pred.a)## [1] "knnReg"pred.a is an object of class knnReg. We can look at the structure of it using the str command:
str(pred.a)## List of 7
## $ call : language FNN::knn.reg(train = dtrain.x, test = dtest.x, y = dtrain.y, k = 5)
## $ k : num 5
## $ n : int 8
## $ pred : num [1:8] 16.4 13 26.5 19.5 23.4 ...
## $ residuals: NULL
## $ PRESS : NULL
## $ R2Pred : NULL
## - attr(*, "class")= chr "knnReg"Most notably, pred.a contains a pred attribute which is the predictions that it made on the testing data. It is now time to examine these predictions to see how accurate they are.
Let’s start by making a copy of our dataset containing the true values of the dependent variable mpg for the testing data. This dataset was called dtest.y and the new copy of it will be called dtest.y.results:
dtest.y.results <- dtest.yNext, we will add the predictions made in pred.a to the new dtest.y.results dataset:
dtest.y.results$k5.pred <- pred.a$predAbove, we stored the predictions made by the KNN model (which were stored in pred.a$pred) as the variable k5.pred in the new dataset dtest.y.results.
We are ready to look at the predictions.
10.5.1.1 Examine predictions
To look at the predictions, we simply view the entire dtest.y.results dataset. For this, we’ll use the head command. We will specify n, the number of rows to display, as the total number of rows in the dataset. That way, the computer will display all of the rows in the dataset:
head(dtest.y.results,n=nrow(dtest.y.results))## mpg k5.pred
## Hornet 4 Drive 21.4 16.38
## Duster 360 14.3 13.04
## Merc 230 22.8 26.54
## Merc 280C 17.8 19.46
## Toyota Corona 21.5 23.38
## Pontiac Firebird 19.2 14.12
## Fiat X1-9 27.3 28.40
## Volvo 142E 21.4 24.24Above, we see the eight cars in the testing dataset, their true mpg values, and the predictions made about each one.
10.5.1.2 RMSE
As you now know from before, RMSE (root mean square error) is a very common metric that is used to calculate the accuracy of a predictive regression model, meaning when the dependent variable is a continuous numeric variable.
Let’s calculate the RMSE for the predictive model we just made. To do this, we use the rmse function from the Metrics package and we feed the actual and predicted values into the function:
if (!require(Metrics)) install.packages('Metrics')
library(Metrics)
rmse(dtest.y.results$mpg,dtest.y.results$k5.pred)## [1] 3.204442Above, we see that the RMSE of this model on this particular testing data is 3.2. When we used linear regression in our previous tutorial, the RMSE was 4.9. So far, KNN seems better than linear regression for making predictions on this data.
10.5.1.3 Discretize and check
Another way that we can check our model’s accuracy is to discretize the data. This means that we will sort the data into discrete categories. Like we did in a previous assignment, we will just categorize the mpg data into high and low values of mpg. We have decided that a car has high mpg if it has a value of mpg over 22. Let’s do this first for the true values of mpg in the testing data:
dtest.y.results$high.mpg <- ifelse(dtest.y.results$mpg>22,1,0)The value of the new variable above will be 1 for all cars with mpg greater than 22 and 0 for all cars with mpg less than or equal to 22.
Below, we’ll do the same for the predicted values of mpg (which are saved as k5.pred):
dtest.y.results$high.mpg.k5.pred <- ifelse(dtest.y.results$k5.pred>22,1,0)Let’s again view the dataset now that these two new variables have been added:
head(dtest.y.results, n=nrow(dtest.y.results))## mpg k5.pred high.mpg
## Hornet 4 Drive 21.4 16.38 0
## Duster 360 14.3 13.04 0
## Merc 230 22.8 26.54 1
## Merc 280C 17.8 19.46 0
## Toyota Corona 21.5 23.38 0
## Pontiac Firebird 19.2 14.12 0
## Fiat X1-9 27.3 28.40 1
## Volvo 142E 21.4 24.24 0
## high.mpg.k5.pred
## Hornet 4 Drive 0
## Duster 360 0
## Merc 230 1
## Merc 280C 0
## Toyota Corona 1
## Pontiac Firebird 0
## Fiat X1-9 1
## Volvo 142E 1And again, you can inspect the entire dataset yourself by running the following command in the console:
View(dtest.y.results)Now that we have successfully discretized our data, we can make a confusion matrix that shows how many predictions were correct and incorrect:
with(dtest.y.results,table(high.mpg,high.mpg.k5.pred))## high.mpg.k5.pred
## high.mpg 0 1
## 0 4 2
## 1 0 2Above, we see that at the threshold of 22:
- 4 cars truly have low
mpgand were correctly predicted to have lowmpg(top left). - 0 cars that truly have high
mpgwere incorrectly predicted to have lowmpg(bottom left). - 2 cars that truly have low
mpgwere incorrectly predicted to have highmpg(top right). - 2 cars that truly have high
mpgwere correctly predicted to have highmpg(bottom right).
Keep reading to see how the same question—predicting mpg values—can be answered using a different method.
10.5.2 Regression tree
We already encountered decision trees in our earlier work together.
Below, we will review the use of a decision tree for the use of regression, which is called a regression tree. Then, we will create a random forest model, which is an extension of the decision tree concept.
For our regression tree, we will continue to use the same training (dtrain) and testing (dtest) data that we used earlier for KNN.
10.5.2.1 Train tree
Since we already have prepared and divided our scaled training and testing datasets, we can make the regression tree right away.
We’ll load the following packages:
if (!require(rpart)) install.packages('rpart')
library(rpart)
if (!require(rattle)) install.packages('rattle')
library(rattle)And here we’ll make the decision tree, called tree1:42
tree1 <- rpart(mpg ~ ., data=dtrain, method = 'anova')Above, here’s what we are telling the computer:
tree1 <-– Save the created regression tree with the nametree1rpart– This is the function that creates a regression tree for us.mpg ~ .– This is the regression formula. We first specify the dependent variable, then write a~, then all independent variables. If we want to use all remaining variables in the dataset (meaning all except the already-specified dependent variable) as independent variables, we can just write a dot after the~symbol, which is what we do here.data=dtrain– This tells therpartfunction which data to use to train the model.method = 'anova'– This tells therpartfunction that we want it to do regression instead of classification or something else.
Now that we have trained a regression tree and saved the result, we can examine it visually.
10.5.2.2 Visualize tree
The code below allows us to inspect the way the computer analyzed our training data and how it plans to make predictions on new data (either our testing data or other fresh data we input).
fancyRpartPlot(tree1, caption = "Regression Tree")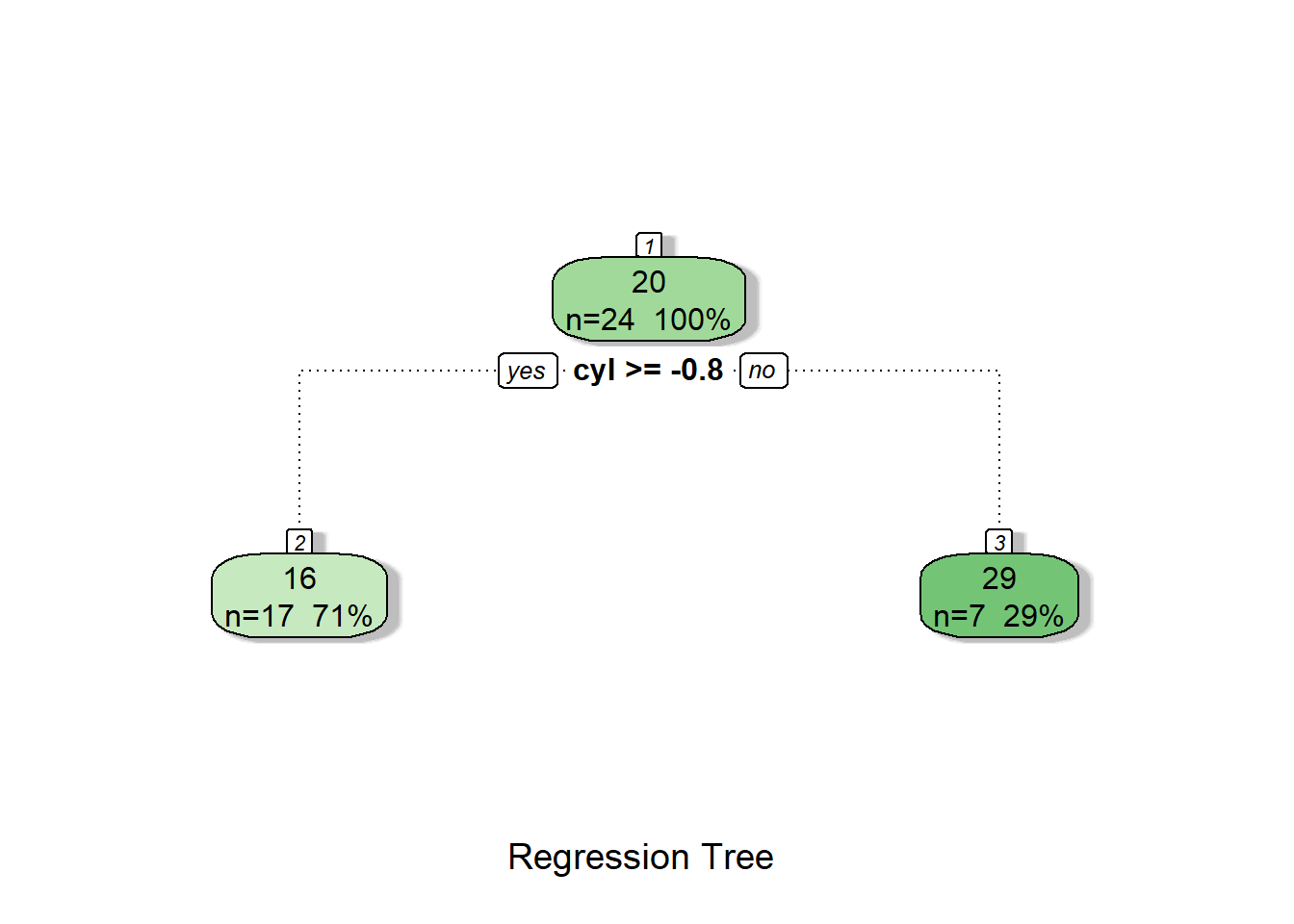
We see that our decision tree is just using a single variable—cyl—to make predictions. If we had more complicated data, the decision tree would like have more steps to it.
10.5.2.3 Variable importance
We can also see a ranking of how useful each variable was in helping us make predictions on this data. For this, we use the varImp function from the caret package:
if (!require(caret)) install.packages('caret')
library(caret)
(varimp.tree1 <- varImp(tree1))## Overall
## cyl 0.7380398
## disp 0.6820361
## hp 0.6366060
## vs 0.5069527
## wt 0.6582077
## drat 0.0000000
## qsec 0.0000000
## am 0.0000000
## gear 0.0000000
## carb 0.0000000Above, we have calculated the variable importance list of tree1 (our saved result) and we saved that list as varimp.tree1. We then put parentheses around the entire command to instruct the computer to also display varimp.tree1 to us.
The list above is also showing us that cyl was the most useful variable for training the model and it is likely to be the most useful variable for making predictions.
10.5.2.4 Examine predictions
Now it is time to make predictions on our testing data. We’ll use the same predict command that you have seen before:
dtest$tree1.pred <- predict(tree1, newdata = dtest)Above, we are adding a variable called tree1.pred to our dtest dataset which will contain the predicted values from the regression tree model. The predict command is what generates the predictions for us, taking as arguments the already-made regression tree (tree1) and the new data to plug into the tree (dtest).
Let’s inspect the predictions:
head(dtest[c("mpg","tree1.pred")], n=nrow(dtest))## mpg tree1.pred
## Hornet 4 Drive 21.4 16.28824
## Duster 360 14.3 16.28824
## Merc 230 22.8 28.61429
## Merc 280C 17.8 16.28824
## Toyota Corona 21.5 28.61429
## Pontiac Firebird 19.2 16.28824
## Fiat X1-9 27.3 28.61429
## Volvo 142E 21.4 28.61429The Toyota Corona had a true mpg of 21.5 and was predicted to have an mpg of 28.6. This prediction was made by the regression tree.
10.5.2.5 RMSE
Like with our KNN model, we can again calculate the RMSE for this regression tree model:
if (!require(Metrics)) install.packages('Metrics')
library(Metrics)
rmse(dtest$mpg,dtest$tree1.pred)## [1] 4.730741This result is worse than for our KNN model.
10.5.2.6 Discretize and check
Like we did with KNN, we can go through the very same discretization process that will lead us to a confusion matrix.
Discretize the true dependent variable:
dtest$high.mpg <- ifelse(dtest$mpg>22,1,0)Discretize the predictions:
dtest$tree1.pred.high <- ifelse(dtest$tree1.pred > 22, 1, 0)Create, save, and display a confusion matrix:
(cm1 <- with(dtest,table(tree1.pred.high,high.mpg)))## high.mpg
## tree1.pred.high 0 1
## 0 4 0
## 1 2 210.5.3 Random forest regression
Now that we have created a decision tree and compared its results to the KNN results, it is time to make a collection of decision/regression trees, which is called a random forest model. With this random forest model, the computer will make 1000 regression trees for us and combine them together to help us make predictions.
To do this, will use fairly familiar code, but from a different package. We will use the randomForest function from the randomForest package:
if (!require(randomForest)) install.packages('randomForest')
library(randomForest)
rf1 <- randomForest(mpg ~ .,data=dtrain, proximity=TRUE,ntree=1000)Here’s what we did above:
- Load
randomForestpackage. - Save the result of a random forest model called
rf1. We created this by specifyingmpgas the dependent variable and all other variables as the independent variable within therandomForestfunction. We set the data used in the model asdtrain, as we have done before. - Finally, we set
proximity=TRUE, which I will not elaborate on at this time; and we specified thatntree, the number of individual regression trees we want to create to make the entire random forest model, should be 1000.
Visualizing this result would not be easy, so we’ll skip straight to looking at the ranking of variable importance in our saved random forest model.
10.5.3.1 Variable importance
We will calculate variable importance just like we have before:
if (!require(caret)) install.packages('caret')
library(caret)
(varimp.rf1 <- varImp(rf1))## Overall
## cyl 194.99475
## disp 218.48957
## hp 146.24381
## drat 61.58509
## wt 191.62804
## qsec 33.43001
## vs 31.46635
## am 12.37963
## gear 22.18344
## carb 22.69941Above, we see in this unsorted list that disp is the most useful variable to help make predictions in this random forest model.
10.5.3.2 Examine predictions
Like we did with the single regression tree, we can again use the predict command to calculate predictions on our testing data:
dtest$rf.pred <- predict(rf1, newdata = dtest)And we can examine the predictions here:
head(dtest[c("mpg","rf.pred")], n=nrow(dtest))## mpg rf.pred
## Hornet 4 Drive 21.4 17.34312
## Duster 360 14.3 14.67998
## Merc 230 22.8 22.31952
## Merc 280C 17.8 18.47047
## Toyota Corona 21.5 23.33027
## Pontiac Firebird 19.2 14.15730
## Fiat X1-9 27.3 28.67597
## Volvo 142E 21.4 23.4344710.5.3.3 RMSE
Once again, we will calculate RMSE:
if (!require(Metrics)) install.packages('Metrics')
library(Metrics)
rmse(dtest$mpg,dtest$rf.pred)## [1] 2.551815This result of approximately 2.6 is lower—and therefore better—than the other models we have tried so far!
10.5.3.4 Discretize and check
We can again discretize our actual and predicted values to get a confusion matrix.
Discretize actual values:
dtest$high.mpg <- ifelse(dtest$mpg>22,1,0)Discretize predicted values:
dtest$rf1.pred.high <- ifelse(dtest$rf.pred > 22, 1, 0)Create, save, and display confusion matrix:
(cm1 <- with(dtest,table(rf1.pred.high,high.mpg)))## high.mpg
## rf1.pred.high 0 1
## 0 4 0
## 1 2 210.5.4 Regression wrap-up
In this section, we looked at three different ways to make predictions on continuous numeric data:
- k-nearest neighbors regression
- regression tree
- random forest regression
All of these methods gave us predicted values for our testing data that we could then compare to the true values for the testing data. Comparing these values using inspection of raw data, RMSE, and confusion matrices allows us to decide which model is best and whether any of them are useful to us.
10.6 Classification techniques
When we want to predict categories as our outcome of interest (instead of a continuous numeric variable as we did earlier in this tutorial), we do what is called classification. With classification, the dependent variable has various categories (not numbers) as its levels. Here are some examples:
| Variable | Levels (possible values that a person/observation can have for this variable) |
|---|---|
| Miles per gallon | high, low |
| Favorite ice cream flavor | chocolate, vanilla, other |
| Marital status | single, married, divorced, other |
Previously, we used logistic regression for classification. In this tutorial, we will use KNN, decision trees, and random forest for the same goal of classification. Unlike with logistic regression43 with other classification algorithms, we could have more than two classes we are trying to predict (like high, medium, low), if we wanted.
10.6.1 Prepare and divide data
Let’s use the same training-testing division from before. However, we need to change our dependent variable into one that is categorical (this is of course not required if your dataset already has a categorical dependent variable). We’ll do that below, categorizing observations with mpg greater than 22 as having high mpg and those less than or equal to 22 as having low mpg.
dtrain$high.mpg <- ifelse(dtrain$mpg>22,1,0)Now our new variable high.mpg has been created and added to our dataset. This will be our dependent variable throughout the classification section of this tutorial. We are no longer using mpg as the dependent variable. Therefore, we should remove mpg from our dataset before we continue:
dtrain$mpg <- NULLAnd we’ll do the very same procedure for the testing data:
dtest$high.mpg <- ifelse(dtest$mpg>22,1,0)
dtest$mpg <- NULLRemember that if your dataset already contains a categorical dependent variable, you do not need to do the steps above to create a binary dependent variable.
Let’s see if we ended up with the variables that we wanted in dtrain:
names(dtrain)## [1] "cyl" "disp" "hp"
## [4] "drat" "wt" "qsec"
## [7] "vs" "am" "gear"
## [10] "carb" "high.mpg"Above, we see that high.mpg is there and mpg has been removed. The same independent variables as before are there.
In dtest, we have some of the leftover additional variables from before when we did regressions. Let’s remove these:
dtest <- dtest %>% select(names(dtrain))Above, we used the select command that we used earlier, but this time we just told it that dtest should contain all of the variables that the dtrain data contains!
Let’s double-check:
names(dtest)## [1] "cyl" "disp" "hp"
## [4] "drat" "wt" "qsec"
## [7] "vs" "am" "gear"
## [10] "carb" "high.mpg"As a final preparatory step, let’s view the first few rows of our testing and training data, to make sure it is ready for classification:
head(dtrain)## cyl disp
## Merc 280 -0.2357706 -0.5638586
## AMC Javelin 0.8959283 0.5129397
## Mazda RX4 Wag -0.2357706 -0.6238562
## Toyota Corolla -1.3674695 -1.3256698
## Datsun 710 -1.3674695 -1.0343658
## Maserati Bora 0.8959283 0.4892564
## hp drat
## Merc 280 -0.4177053 0.59197680
## AMC Javelin -0.0428119 -0.76027676
## Mazda RX4 Wag -0.5982095 0.55685333
## Toyota Corolla -1.2230318 1.11882884
## Datsun 710 -0.8342535 0.46904466
## Maserati Bora 2.5259020 -0.07536911
## wt qsec
## Merc 280 0.1552003 0.5275958
## AMC Javelin 0.1505536 -0.1158137
## Mazda RX4 Wag -0.3698786 -0.2959684
## Toyota Corolla -1.3363954 1.5570511
## Datsun 710 -0.8856640 0.7270528
## Maserati Bora 0.2760149 -1.8530194
## vs am
## Merc 280 1.3844373 -0.9004984
## AMC Javelin -0.6922187 -0.9004984
## Mazda RX4 Wag -0.6922187 1.0642254
## Toyota Corolla 1.3844373 1.0642254
## Datsun 710 1.3844373 1.0642254
## Maserati Bora -0.6922187 1.0642254
## gear carb
## Merc 280 0.3148618 0.5702471
## AMC Javelin -0.9445853 -0.6198338
## Mazda RX4 Wag 0.3148618 0.5702471
## Toyota Corolla 0.3148618 -1.2148742
## Datsun 710 0.3148618 -1.2148742
## Maserati Bora 1.5743088 2.9504088
## high.mpg
## Merc 280 0
## AMC Javelin 0
## Mazda RX4 Wag 0
## Toyota Corolla 1
## Datsun 710 1
## Maserati Bora 0head(dtest)## cyl disp
## Hornet 4 Drive 0.2820380 0.4355138
## Duster 360 1.4101902 1.2867217
## Merc 230 -0.8461141 -0.5425407
## Merc 280C 0.2820380 -0.3188900
## Toyota Corona -0.8461141 -0.7152858
## Pontiac Firebird 1.4101902 1.6205287
## hp drat
## Hornet 4 Drive -0.30867099 -1.2524589
## Duster 360 2.07250519 -0.9604057
## Merc 230 -0.57324612 0.6346541
## Merc 280C -0.07937254 0.6346541
## Toyota Corona -0.53796943 0.1404102
## Pontiac Firebird 0.83782125 -1.2524589
## wt qsec
## Hornet 4 Drive 0.2632441 0.23282431
## Duster 360 0.8296179 -1.49535614
## Merc 230 0.1595419 1.89379774
## Merc 280C 0.6222134 -0.02640276
## Toyota Corona -0.9333202 0.50645288
## Pontiac Firebird 1.2683582 -0.91449549
## vs am
## Hornet 4 Drive 0.5400617 -0.5400617
## Duster 360 -1.6201852 -0.5400617
## Merc 230 0.5400617 -0.5400617
## Merc 280C 0.5400617 -0.5400617
## Toyota Corona 0.5400617 -0.5400617
## Pontiac Firebird -1.6201852 -0.5400617
## gear carb
## Hornet 4 Drive -0.9354143 -0.9025825
## Duster 360 -0.9354143 1.5043042
## Merc 230 0.9354143 -0.1002869
## Merc 280C 0.9354143 1.5043042
## Toyota Corona -0.9354143 -0.9025825
## Pontiac Firebird -0.9354143 -0.1002869
## high.mpg
## Hornet 4 Drive 0
## Duster 360 0
## Merc 230 1
## Merc 280C 0
## Toyota Corona 0
## Pontiac Firebird 0Above, we see that our independent variables are all still scaled as they were initially. And mpg.high—the dependent variable—is coded correctly, with all cars having the value of either 1 (meaning high mpg) or 0 (meaning low mpg).
We are ready to run some classification models.
10.6.2 k-Nearest neighbors classification
The first classification model we will run is k-nearest neighbors (KNN) for classification. Like we did with KNN regression, we have to further divide our data so that the independent variables and dependent variable are in separate datasets for both the training and testing data:
dtrain.x <- dtrain %>% select(-high.mpg) # remove DV
dtrain.y <- dtrain %>% select(high.mpg) # keep only DV
dtest.x <- dtest %>% select(-high.mpg) # remove DV
dtest.y <- dtest %>% select(high.mpg) # keep only DVAbove, we created the same four datasets that we did when doing KNN regression, earlier in this tutorial.
Next, we’ll train a KNN classification model and make predictions with it on our testing data:
if (!require(class)) install.packages('class')## Warning: package 'class' was built under
## R version 4.2.3library(class)
pred.a <- knn(train = dtrain.x, test = dtest.x,cl = dtrain.y[,1], k=5)Above, we used the knn function from the class package. We again saved our predicted results as pred.a. We gave four arguments to the knn function, which are very similar to when we did KNN regression earlier:
train = dtrain.x– Same as before. These are the independent variables for the training data.test = dtest.x– Same as before. These are the independent variables for the testing data.cl = dtrain.y[,1]– This is the same idea as before. We need to give the computer the dependent variable values for the training data. These values are in the first (and only) column of thedtrain.ydataset, so we specify as such in the square brackets.k=5– This is the number of neighbors we want the model to use. This number will stay the same as before because the size of the training and testing datasets have remained the same.
Our KNN classification results are stored in pred.a and now we can look at its predictions.
10.6.2.1 Examine predictions
Like before, we’ll create a new dataset—this time called dtest.y.results.classification—to hold our actual and predicted values:44
dtest.y.results.classification <- dtest.y
dtest.y.results.classification$high.mpg.pred <- pred.aAnd then we can examine the raw predictions:
head(dtest.y.results.classification, n=nrow(dtest.y.results.classification))## high.mpg high.mpg.pred
## Hornet 4 Drive 0 0
## Duster 360 0 0
## Merc 230 1 1
## Merc 280C 0 0
## Toyota Corona 0 1
## Pontiac Firebird 0 0
## Fiat X1-9 1 1
## Volvo 142E 0 1The Toyota Corona has low mpg in reality (which is what the 0 means under high.mpg in the Toyota Corona row), but it is predicted by the KNN classification model to have high mpg (which is what the 1 means under high.mpg.pred in the Toyota Corona row).
10.6.2.2 Confusion matrix
And we can easily make a confusion matrix by making a table with the two variables we inspected above within our new dtest.y.results.classification dataset:
(cm1 <- with(dtest.y.results.classification,table(high.mpg.pred,high.mpg)))## high.mpg
## high.mpg.pred 0 1
## 0 4 0
## 1 2 210.6.3 Decision tree classification
Continuing with our attempts to create a model to classify our testing data correctly, we will make a decision tree.
We can again use the rpart function to make this tree:45
tree2 <- rpart(high.mpg ~ ., data=dtrain, method = "class")Above, we specified class as the type of tree to make. Other than that, this is the same approach you saw earlier in the regression tree part of the tutorial.
10.6.3.1 Visualize
We can visualize our new tree:
fancyRpartPlot(tree2, caption = "Classification Tree")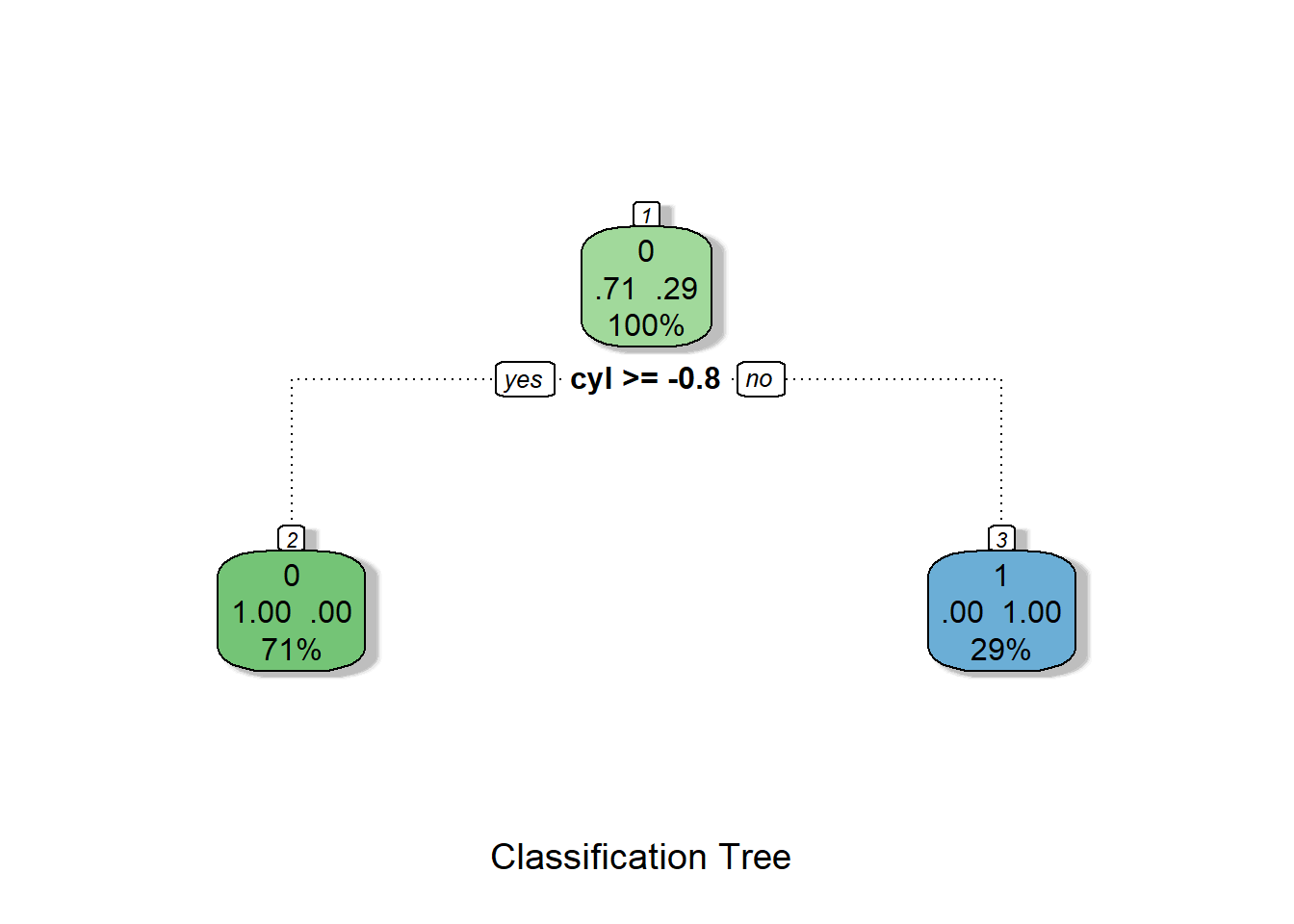
Again, the variable cyl is used to classify the observations.
10.6.3.2 Variable importance
We can rank the importance of the independent variables used to make the decision tree:
if (!require(caret)) install.packages('caret')
library(caret)
(varimp.tree2 <- varImp(tree2))## Overall
## cyl 9.916667
## disp 8.166667
## hp 6.320028
## vs 5.041667
## wt 6.320028
## drat 0.000000
## qsec 0.000000
## am 0.000000
## gear 0.000000
## carb 0.000000Again, cyl is determined to be the most important variable.
10.6.3.3 Examine predictions
Now let’s look at the raw predictions. First, we generate the predictions on our testing data:
dtest$tree2.pred <- predict(tree2, newdata = dtest, type = 'class')Now we can inspect those predictions next to the true values:
head(dtest[c("high.mpg","tree2.pred")],n=nrow(dtest))## high.mpg tree2.pred
## Hornet 4 Drive 0 0
## Duster 360 0 0
## Merc 230 1 1
## Merc 280C 0 0
## Toyota Corona 0 1
## Pontiac Firebird 0 0
## Fiat X1-9 1 1
## Volvo 142E 0 110.6.4 Random Forest
Finally, we will make a random forest model to help us with this classification problem. We will recode the high.mpg variable as a factor variable because that will tell the randomForest to do classification instead of regression. Then we will use the same syntax as before (when we made the random forest regression):
if (!require(randomForest)) install.packages('randomForest')
library(randomForest)
dtrain$high.mpg <- as.factor(dtrain$high.mpg)
rf1 <- randomForest(high.mpg ~ ., data=dtrain,ntree=1000)Now our random forest model is trained and is saved as an object called rf1.
10.6.4.1 Variable Importance
cyl is still the most important variable:
if (!require(caret)) install.packages('caret')
library(caret)
(varimp.rf1 <- varImp(rf1))## Overall
## cyl 2.73150820
## disp 2.00420952
## hp 1.73637235
## drat 0.30027891
## wt 1.42705511
## qsec 0.40029359
## vs 0.44019512
## am 0.03531011
## gear 0.10380430
## carb 0.3901394510.6.4.2 Examine predictions
This procedure should become natural to you. We once again predict the dependent variable for the testing data:
dtest$rf.pred <- predict(rf1, newdata = dtest)And then we examine it:
head(dtest[c("high.mpg","rf.pred")], n=nrow(dtest))## high.mpg rf.pred
## Hornet 4 Drive 0 0
## Duster 360 0 0
## Merc 230 1 0
## Merc 280C 0 0
## Toyota Corona 0 1
## Pontiac Firebird 0 0
## Fiat X1-9 1 1
## Volvo 142E 0 110.6.5 Classification wrap-up
In this section, we looked at three different ways to make predictions on categorical data:
- k-nearest neighbors classification
- decision/classification tree
- random forest classification
All of these methods gave us predicted values for our testing data that we could then compare to the true values for the testing data. Comparing these values using inspection of raw data and confusion matrices allows us to decide which model is best and whether any of them are useful to us. We could also use metrics like accuracy, sensitivity, and specificity to compare the models, as we have done before.
10.7 Assignment
In this week’s assignment, you will use a dataset of your own choosing to predict a dependent variable using the regression and classification methods that were demonstrated in this tutorial.
Please follow these guidelines when deciding which data to use for this assignment:
If you have ready-to-use data of your own, I highly recommend that you use it. This is a great opportunity to further explore a data set that you already have. Those of you doing the data analysis option for your final project in the class can also use this assignment to help develop that project.
If you do not have any data of your own to use or if you simply prefer not to use your own data for this assignment, that is perfectly fine. In this case, please again use the
student-pordata that we have used before in the class.Another good option could be to use the
NHANESdata set which can be accessed from within R.46
In this assignment, there will be less guidance and facilitation than in other assignments you have done in this class. Please try to make your own judgments about what data preparation to use, metrics to use, tests to run, interpretations to provide, and so on. You may also find it useful to refer to previous chapters in this course book.
Important note: In this assignment, you will have the computer randomly split your data into training and testing datasets. Every time you do this, a new random split of the data will occur. This means that your results will be different every time, includng when you Knit your assignment to submit it. As a result, the numbers in your written explanations will not match the numbers in your computer-generated outputs. This is completely fine. Please just write your answers based on the numbers you get initially and then submit your assignment even with the incorrect numbers that are generated when you Knit.
10.7.1 Regression
In this part of the assignment, you will prepare a short report that answers a question that can be solved using the regression techniques demonstrated in this chapter.
Task 1: Articulate a research question that can be answered with regression techniques and using your data for this assignment. Of course, this question should be such that the dependent variable is well-suited to be answered using regression methods.
Task 2: Create and present the results of KNN regression, regression tree, and random forest regression models to answer your research question. Additionally, try to also compare the results of at least three different values of k in your KNN model. Present any relevant visualizations.
Task 3: For each predictive model, evaluate how good each model is at making predictions. Include at least three metrics that you think are most useful to help you compare models.
Task 4: Explain which model is the best and why.
Task 5: Evaluate which independent variables are most important in enabling you to make predictions. Do this only for your random forest model.
Task 6: Address whether your best model is useful to you or not in a practical sense, with regards to your research question.
10.7.2 Classification
Now you will prepare another short report that answers a question that can be solved using classification techniques.
Task 7: Articulate a research question that can be answered with predictive classification techniques using your data for this assignment. Of course, this question should be such that the dependent variable is well-suited to be answered using classification methods.
Task 8: Create and present the results of KNN classification, decision tree, and random forest classification models to answer your research question. Additionally, try to also compare the results of at least three different values of k in your KNN model. Present any relevant visualizations.
Task 9: For each predictive model, evaluate how good each model is at making predictions. Include at least three metrics that you think are most useful to help you compare models.
Task 10: Explain which model is the best and why.
Task 11: Evaluate which independent variables are most important in enabling you to make predictions. Do this only for your random forest model.
Task 12: Address whether your best model is useful to you or not in a practical sense, with regards to your research question.
10.7.3 Make new predictions
Now you will practice making predictions using one of the models that you created earlier in the assignment. Please select either the regression or classification portion (not both) of the assignment above to do the work below.
Task 13: Using your favorite/best-performing model from earlier in the assignment, make predictions for your dependent variable on new data, for which the dependent variable is unknown. Present the results in a confusion matrix. Please see the following notes related to this task.
- You will need to pre-process your new data the same way you pre-processed the data that you used to create the machine learning model in the first place.
- The confusion matrix you present will of course only contain predicted values, because actual values are not known.
- If you are using the
student-por.csvdata, you can click here to download the new data file calledstudent-por-newfake.csvand make predictions on it. - If you are using data of your own, you can a) use real new data that you have, b) make fake data to practice, or c) ask the instructors for suggestions. The true value of the dependent variable for the new data must be unknown.
10.7.4 Follow-up and submission
You have now reached the end of this week’s assignment. The tasks below will guide you through submission of the assignment and allow us to gather questions and feedback from you.
Task 14: Please write any questions you have this week (optional).
Task 15: Write any feedback you have about this week’s content/assignment or anything else at all (optional).
Task 16: Submit your final version of this assignment to the appropriate assignment drop-box in D2L.
Note that even though logistic regression has the word regression in its name, it is only used for classification (predicting a binary outcome), not for regression (predicting a numeric outcome). This ambiguity in its name is unfortunate and can be confusing, so just try to remember that logistic regression is used for classification.↩︎
Do not run this in your RMarkdown or R code file; only in the console directly.↩︎
We do not have to do this additional splitting for most other machine learning techniques that we learn in this class.↩︎
Sometimes the computer might not be able to make a tree for you. In this case, you might need to adjust some more settings in the
rpart(...)function. A good way to start with this could be to run approximately this code:rpart(yourDependentVariable ~ ., data=yourData, control=rpart.control(minsplit=1, minbucket=1, cp=0.001)). Then, gradually increase the values ofminsplit,minbucket, andcp. Usually, the computer uses the following values:minsplit = 20, minbucket = round(minsplit/3), cp = 0.01. This information came from the answer from Travis Heeter in the page titled “The result of rpart is just with 1 root” at https://stackoverflow.com/questions/20993073/the-result-of-rpart-is-just-with-1-root.↩︎We previously used and are now referring to binary logistic regression, which only allows for two possible classes that we want to predict. Binary logistic regression is usually what a person will mean when they say logistic regression. There is also a variant of logistic regression called multinomial logistic regression which is meant for predicting more than two categories of the dependent variable. Multinomial logistic regression could be used to solve classification problems with more than three levels.↩︎
If you instead want to calculate predicted probabilities instead of predicted values, you can use this:
dtest.y.results.classification$high.mpg.prob <- attr(pred.a, "prob")↩︎Sometimes the computer might not be able to make a tree for you. In this case, you might need to adjust some more settings in the
rpart(...)function. A good way to start with this could be to run approximately this code:rpart(yourDependentVariable ~ ., data=yourData, control=rpart.control(minsplit=1, minbucket=1, cp=0.001)). Then, gradually increase the values ofminsplit,minbucket, andcp. Usually, the computer uses the following values:minsplit = 20, minbucket = round(minsplit/3), cp = 0.01. This information came from the answer from Travis Heeter in the page titled “The result of rpart is just with 1 root” at https://stackoverflow.com/questions/20993073/the-result-of-rpart-is-just-with-1-root.↩︎Instructions on how to load and use the NHANES data can be found in section “Load and prepare data” within section “Logistic regression in R” at https://bookdown.org/anshul302/HE902-MGHIHP-Spring2020/LogReg1.html#logistic-regression-in-r. Be sure to choose a reasonable dependent variable for each part of the assignment that would be useful to be able to predict about the future.↩︎