Capítulo 2 Valor informativo de las variables
Uno de los primeros aspectos a considerar en el análisis de grandes cantidades de datos tiene que ver, justamente, con el gran volumen de información disponible. Para un conjunto de individuos podemos tener recopilados datos de multitud de variables y el primer problema al que nos enfrentamos consiste en seleccionar aquellas variables más informativas: ¿qué atributos son los mejores para segmentar la población?
Utilizaremos un ejemplo propuesto por Provost y Fawcett (2013, p. 53-56). Imaginemos que un banco ha recopilado información sobre los individuos a los que ha concedido un préstamo en el pasado. A continuación, se dispone a estudiar esta información para conocer qué atributos permiten predecir si un sujeto devolverá —o no— un préstamo. Para simplificarlo, pensaremos que solo tenemos información sobre dos variables: los «ahorros» (la cantidad de dinero que la persona tenía en el banco en el momento de concesión del préstamo; para hacerlo sencillo, dividiremos la población en dos grupos: los que tenían ahorrados menos de 50 000 € y los que tenían más) y la disponibilidad de la «vivienda» (en este caso tendremos tres valores: en propiedad, en alquiler u otras situaciones).
El problema consiste en determinar cuál de las dos variables («ahorros» o «vivienda») es más informativa para decidir si conceder o no un préstamo a un nuevo cliente. El cuadro 2.1 presenta los datos históricos de una treintena de clientes de la entidad. Por ejemplo, el primer cliente, que acabó siendo moroso, tenía menos de 50 000 € ahorrados y la vivienda en propiedad en el momento de la concesión del préstamo.
| Ahorros | Vivienda | Moroso |
|---|---|---|
| Menos_50000 | Propiedad | Si |
| Menos_50000 | Propiedad | Si |
| Menos_50000 | Propiedad | Si |
| Menos_50000 | Propiedad | Si |
| Menos_50000 | Propiedad | Si |
| Menos_50000 | Propiedad | Si |
| Menos_50000 | Propiedad | Si |
| Menos_50000 | Alquiler | Si |
| Menos_50000 | Alquiler | Si |
| Menos_50000 | Alquiler | Si |
| Menos_50000 | Alquiler | Si |
| Menos_50000 | Otros | Si |
| Mas_50000 | Otros | Si |
| Mas_50000 | Otros | Si |
| Mas_50000 | Otros | Si |
| Mas_50000 | Otros | Si |
| Menos_50000 | Propiedad | No |
| Mas_50000 | Alquiler | No |
| Mas_50000 | Alquiler | No |
| Mas_50000 | Alquiler | No |
| Mas_50000 | Alquiler | No |
| Mas_50000 | Alquiler | No |
| Mas_50000 | Alquiler | No |
| Mas_50000 | Otros | No |
| Mas_50000 | Otros | No |
| Mas_50000 | Otros | No |
| Mas_50000 | Otros | No |
| Mas_50000 | Otros | No |
| Mas_50000 | Otros | No |
| Mas_50000 | Otros | No |
El primer paso consiste en calcular la entropía de cada grupo de individuos. La entropía hace referencia al desorden, a la impureza dentro del grupo. Cuanto más impuro o diverso es un grupo, más entropía contiene. La fórmula es la siguiente:
\(entropía = –[p_{1} × log_{2} (p_{1}) + p_{2} × log_{2} (p_{2}) + \dotso ]\)
Cada p\(_{i}\) es la probabilidad (la frecuencia relativa) de tener el atributo i y oscila entre 1 (cuando todos los sujetos tienen el atributo) y 0 (cuando no lo tiene ninguno). Los puntos suspensivos simplemente indican que puede haber más de dos atributos.
El valor de la entropía es máximo (1) cuando la probabilidad de un evento binario es 0,5. Si tiramos una moneda al aire, la probabilidad de obtener cara o cruz es de 0,5. La entropía es máxima y refleja la incerteza sobre el resultado.
En el caso de la morosidad:
\(p (morosidad) = 16/30 = 0,53\)
\(p (no.morosidad) = 14/30 = 0,47\)
La entropía sería la siguiente:
\(entropía (morosidad) = – [(0,53 × –0,9) + (0,47 × –1,1)] = 0,99\)
La entropía es muy elevada (0,99) ya que el grupo es impuro en el sentido de que hay una elevada división entre morosos y no morosos. En el caso contrario, si todos los clientes fueran morosos (o si ninguno lo fuera), la entropía tendería a 0.
Nosotros deseamos medir cuan informativa es una variable, es decir, cuánta información nos proporciona sobre el valor de la variable que queremos predecir. La ganancia informativa (information gain, IG) mide en qué medida un atributo reduce la entropía en los segmentos que crea. Imaginemos que la variable que utilizamos para dividir el grupo tiene k valores. En este caso, el grupo inicial (progenitor) se dividirá en k subgrupos. El valor informacional del atributo vendrá dado por el incremento en la pureza de los k subgrupos respecto a la población inicial.
Siguiendo con el ejemplo, calculamos la entropía de los dos subgrupos de clientes creados en función de sus «ahorros» (se muestran en la figura 2.1):
\(entropía (< 50.000 €) = – [(0,92 × –0,1) + (0,08 × –3,7)]= 0,39\)
\(entropía (> 50 000 €) = – [(0,24 × –2,1) + (0,76 × –0,4)]= 0,79\)
Con estos datos ya podemos calcular la ganancia informativa (IG) de acuerdo con la siguiente fórmula:
\(IG = entropía (progenitor) – [p(c_{1}) × entropía (c_{1}) + p(c_{2}) × entropía (c_{2}) + … ]\)
La entropía de cada uno de los subgrupos generados (c\(_{i}\)) se pondera multiplicándola por la proporción de casos que pertenecen a ese subgrupo, p(c\(_{i}\)). Siguiendo con el ejemplo anterior, calculamos la ganancia informativa resultado de dividir a los clientes en dos subgrupos en función de sus «ahorros»:
\(IG = 0,99 – [(0,43 × 0,39) + (0,57 × 0,79)] = 0,37\)
Vemos que la división de los clientes en dos subgrupos, en función de sus ahorros, reduce sustancialmente la entropía. En términos de un modelo predictivo, podemos decir que este atributo (los «ahorros») ofrece mucha información sobre el valor de la variable que deseamos predecir (la «morosidad»).
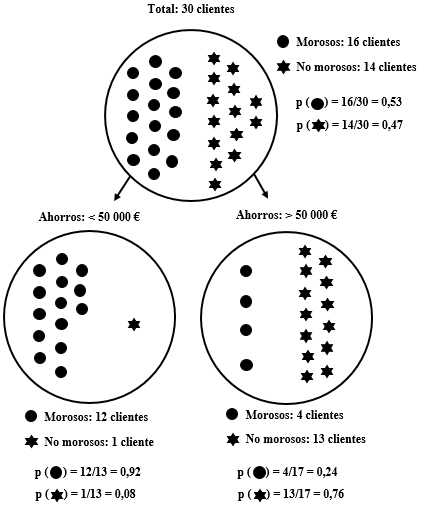
Figure 2.1: Datos de morosidad de 30 clientes de un banco en función de sus ahorros
A continuación, analizaremos qué ocurre si dividimos el grupo en función de la otra variable de la que tenemos datos, la disponibilidad de la «vivienda». En este caso, la variable tiene tres valores: en propiedad, en alquiler u otros.
\(entropía (progenitor) = 0,99\)
\(entropía (propiedad) = – [(0,88 × –0,2) + (0,12 × –3,0)] = 0,54\)
\(entropía (alquiler) = – [(0,40 × –1,3) + (0,60 × –0,7)] = 0,97\)
\(entropía (otros) = – [(0,42 × –1,3) + (0,58 × –0,8)] = 0,98\)
\(IG = 0,99 – [(0,27×0,54) + (0,33×0,97) + (0,40×0,98)] = 0,13\)
La variable «vivienda» proporciona alguna ganancia informativa, pero no tanta como la variable «ahorros». Intuitivamente, podemos observar que mientras que en el grupo de clientes que tiene la vivienda en propiedad (el de la izquierda) se ha reducido sustancialmente la entropía, los otros dos grupos (en alquiler y otros) no son mucho más puros que el grupo inicial.
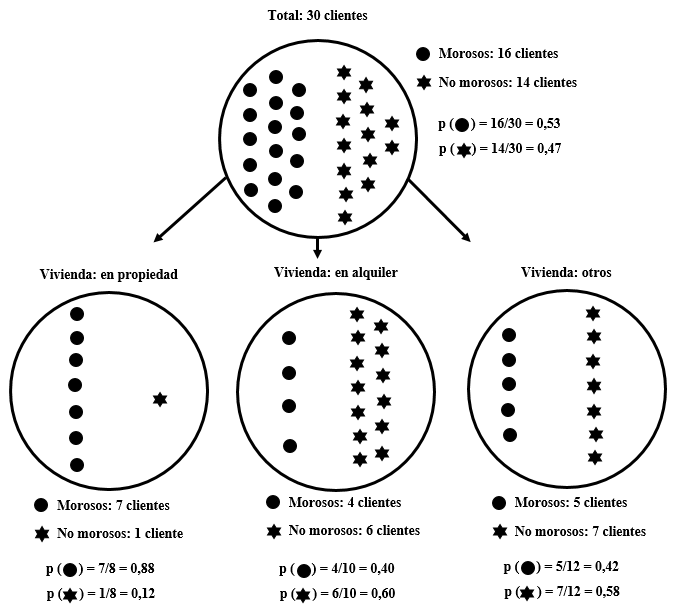
Figure 2.2: Datos de morosidad de 30 clientes de un banco en función de la disponibilidad de su vivienda
Por tanto, a partir de un dataset con objetos descritos por atributos y una variable a predecir, podemos determinar qué atributo es el más informativo para la predicción. Asimismo, podemos ordenar los atributos por su valor informativo. Esto nos ayuda a entender mejor los datos y a reducir el volumen de datos a analizar, seleccionando aquellos atributos que procesaremos.
2.1 Cálculo de la ganancia informativa con R
Para calcular la entropía y la ganancia informativa con R utilizaremos el paquete FSelectorRcpp. Utilizaremos como ejemplo el mismo dataset sobre morosidad.
El siguiente script contiene tres funciones para llamar a la librería (previamente se ha de haber instalado), importar el dataset (en un objeto que denominamos morosidad) y pedir que nos calcule la ganancia informativa. En esta última orden, indicamos que la categoría a determinar es la de «Moroso» (véase en el cuadro 2.1 que es la tercera columna) y que el objeto con los datos se llama morosidad.
library(FSelectorRcpp) # Llamamos al paquete
morosidad <- read.table("morosidad.txt", header=T, sep = "\t") # Importamos el dataset
# Pedimos la ganancia informativa de la variable que queremos predecir
# El símbolo ~ se obtiene con AltGr + 4 (dos veces)
information_gain(Moroso ~ ., morosidad)## attributes importance
## 1 Ahorros 0.26423766
## 2 Vivienda 0.09443674Vemos que la variable más informativa son los «ahorros» y, en menor medida, la «vivienda». Las cifras que facilita FSelectorRcpp no coinciden con las que habíamos obtenido anteriormente porque, en lugar de utilizar el \(log_{2}\), este paquete utiliza el logaritmo natural \(ln\).
2.2 Ejercicio 2. ¿Es venenosa esta seta?
Hemos recogido información sobre 16 variedades de setas. Para cada una de ellas conocemos el «color», el «tamaño» y la «forma», así como si es una variedad «comestible» o «venenosa». El objetivo de la actividad es determinar qué características de las setas («color», «tamaño» o «forma») aportan más información sobre su carácter comestible o venenoso. Utiliza el paquete FSelectorRcpp para resolver el ejercicio.
| Color | Tamano | Forma | Comestible |
|---|---|---|---|
| Amarillo | Pequena | Redonda | Si |
| Amarillo | Pequena | Redonda | No |
| Verde | Pequena | Irregular | Si |
| Verde | Grande | Irregular | No |
| Amarillo | Grande | Redonda | Si |
| Amarillo | Pequena | Redonda | Si |
| Amarillo | Pequena | Redonda | Si |
| Amarillo | Pequena | Redonda | Si |
| Verde | Pequena | Redonda | No |
| Amarillo | Grande | Redonda | No |
| Amarillo | Grande | Redonda | Si |
| Amarillo | Grande | Redonda | No |
| Amarillo | Grande | Redonda | No |
| Amarillo | Grande | Redonda | No |
| Amarillo | Pequena | Irregular | Si |
| Amarillo | Grande | Irregular | Si |
Es posible realizar esta misma actividad con un dataset más completo que contiene información sobre 8124 variedades de setas disponible en: http://archive.ics.uci.edu/ml/datasets/Mushroom. Cada seta está representada en una fila con datos en 23 columnas. La primera columna indica si es comestible (e, edible) o venenosa (p, poisonous). Las 22 variables restantes indican características como la forma, la textura, el color, el olor, etc. Todas las variables son categóricas discretas (adoptan un único valor). Por ejemplo, la segunda columna indica la forma del sombrero (cap shape) y puede adoptar seis valores (bell=b, conical=c, convex=x, flat=f, knobbed=k, sunken=s). El objetivo de la actividad es determinar cuál de la 22 características es la que aporta más información sobre el carácter comestible o venenoso de una seta.