Capítulo 4 Clasificadores bayesianos
Muchos algoritmos de clasificación se basan en «entrenar» un modelo para que, a continuación, haga predicciones usando los ejemplos que ya han sido clasificados. Un modelo de este tipo puede servir, por ejemplo, para decidir si un correo electrónico es spam o no. Muchos de estos modelos se basan en la estadística bayesiana, un tipo de inferencia estadística en la que las evidencias u observaciones se emplean para actualizar o inferir la probabilidad de que una hipótesis sea cierta.
Comencemos con un ejemplo relativo a dos sucesos independientes. Si tiro una moneda al aire dos veces consecutivas, ¿cuál es la probabilidad de obtener dos caras? Dado que el resultado del primer lanzamiento (A) no influye sobre el resultado del segundo (B):
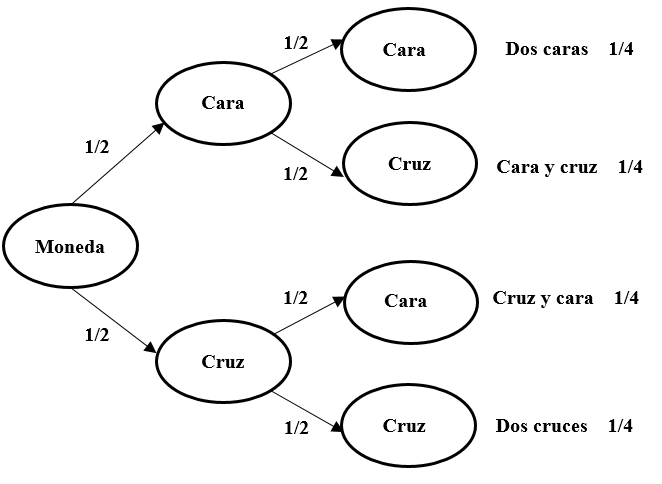
Figure 4.1: Posibles resultados de lanzar una moneda en dos ocasiones consecutivas
\[p (AB) = p (A) × p (B) = 1/2 × 1/2 = 1/4\]
La probabilidad conjunta de dos sucesos independientes (A y B) es la probabilidad de que se dé A multiplicada por la probabilidad de que ocurra B dado A y se representa con la siguiente fórmula:
\[p (AB) = p (A) × p (B | A)\]
En el caso del lanzamiento de la moneda, la probabilidad de que salgan dos caras es igual a la probabilidad de que salga cara \(p (A) = 0,5\), multiplicada por la probabilidad de que vuelva a salir cara si en el primer lanzamiento ha salido una cara \(p (B | A) = 0,5\). Por tanto, \(0,5 × 0,5 = 0,25\).
Dado que A y B son sucesos independientes, siguiendo la misma lógica podemos afirmar que la probabilidad conjunta \(p (AB)\) es la probabilidad de que se dé B multiplicada por la probabilidad de que ocurra A dado B:
\[p (AB) = p (B) × p (A | B)\]
Por tanto:
\[p (A) × p (B | A) = p (AB) = p (B) × p (A | B)\]
De lo anterior, se deriva el teorema de Bayes:
\[p (A | B) = \frac{p (B | A) × p (A)} {p (B)}\]
Veamos un ejemplo. Asumamos que la probabilidad de padecer cáncer es de 0,05. Es decir, el 5% de la población padece cáncer \(p (A) = 0,05\). Ahora asumamos que la probabilidad de ser fumador es de 0,10. Es decir, el 10% de la población fuma \(p (B) = 0,10\). Sabemos que el 20% de los pacientes con cáncer son fumadores, de manera que \(p (fumador | cáncer) = 0,20\). O, lo que es lo mismo, \(p (B | A) = 0,20\). ¿Cuál es la probabilidad de padecer cáncer si se es fumador? Aplicando el teorema de Bayes:
\[p(\text{cáncer|fumador}) = \frac{p (\text{fumador│cáncer}) × p (\text{cáncer})} {p (\text{fumador})} = \frac {0,20 × 0,05} {0,10} = 0,10\]
Es decir, puesto que la ratio de tabaquismo es el doble entre las personas que padecen cáncer que en el conjunto de la población, se duplica la probabilidad de padecer cáncer entre las personas que fuman.
Veamos un segundo ejemplo. Imaginemos un test de dopaje con una fiabilidad del 95%. Es decir, el test clasifica correctamente al 95% de los atletas que se dopan y al 95% de los que no. Supongamos que 1 de cada 50 atletas (el 2%) recurre al dopaje. Los resultados de aplicar el test a 1000 atletas se muestran en la figura 4.2.
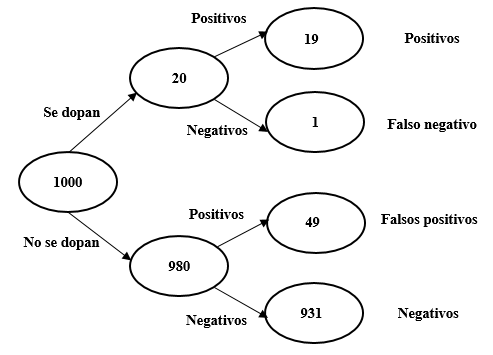
Figure 4.2: Resultados de aplicar a 1000 atletas el test de dopaje
El test nos ofrecerá 19+49 = 68 positivos. Sin embargo, solo 19 corresponden realmente a atletas que se dopan (19/68 = 28%). El 72% restante son falsos positivos. A pesar del 95% de fiabilidad del test, la mayoría de los positivos son falsos.
Es importante no confundir la probabilidad de que un test arroje un resultado positivo dado que el atleta se dopa \(p (A | B) = 95\%\) con la probabilidad de que un atleta se dope dado un test positivo \(p (B | A) = 28\%\). Veamos el mismo resultado aplicando el teorema de Bayes:
\[p (B | A)= \frac{p (A | B) × p (B)} {p (A)}\]
\[p(\text{dopaje|positivo}) = \frac{p (\text{positivo│dopaje}) × p(\text{dopaje})} {p (\text{positivo})} = \frac{0,95 × 0,02} {0,068} = 0,28\]
El teorema de Bayes tiene múltiples aplicaciones en ciencia de datos, entre otras con finalidades de clasificación. Una de estas utilidades es la construcción de detectores de correo basura (spam). El sistema consiste en analizar las características de los correos spam: quién es el emisor, número de destinatarios, existencia de archivos adjuntos, errores ortográficos, palabras que aparecen en el mensaje, etc.
Nos centraremos ahora en la aparición de palabras, por ejemplo, los términos «barato» y «comprar». En una muestra de 100 mensajes, observamos que 25 son spam y 75 no lo son. De los 25 mensajes que sí son spam, la palabra «barato» aparece en 20 de ellos. Entre los 75 que no son spam, la palabra «barato» aparece en 5 de ellos.
\[p (\text{barato | spam}) = 20/25 = 0,80\]
\[p (\text{barato | no spam}) = 5/75 = 0,066\]
En el caso de la palabra «comprar», su probabilidad de aparición en un mensaje de spam es 15/25 y en un mensaje que no sea spam de 10/75.
\[p (\text{comprar | spam}) = 15/25 = 0,60\]
\[p (\text{comprar | no spam}) = 10/75 = 0,133\]
Si suponemos que la aparición de las dos palabras son sucesos independientes, la probabilidad de que aparezcan conjuntamente será el producto de las probabilidades individuales. Así, en el caso de los mensajes de spam, la probabilidad de que aparezcan juntas ambas palabras es la siguiente:
\[p (\text{barato y comprar | spam}) = 0,8 × 0,6 = 0,48\]
La probabilidad es de 0,48, es decir, que 12 de cada 25 mensajes de spam contendrán las palabras «barato» y «comprar» simultáneamente.
Siguiendo el mismo procedimiento, podemos calcular la frecuencia conjunta de ambas palabras en mensajes que no sean spam. Vemos que la probabilidad es muy inferior, no llega ni a un correo electrónico de los 75:
\[p (\text{barato y comprar | no spam}) = 0,066 × 0,133 = 0,009\]
Aplicando el teorema de Bayes ya podemos calcular la probabilidad de que un mensaje sea spam —o no lo sea— según la aparición de la palabra «barato», «comprar» o ambas.
\[p (\text{spam | barato}) = \frac{p (\text{barato │ spam}) × p(\text{spam})} {p (\text{barato})} = \frac{0,8 × 0,25} {0,25} = 0,80\]
\[p(\text{spam | comprar}) = \frac{p (\text{comprar │ spam}) × p(\text{spam})} {p (\text{comprar})} = \frac{0,6 × 0,25} {0,25} = 0,60\]
Finalmente, podemos calcular la posibilidad de que aparezcan las dos palabras conjuntamente:
\(p(\text{spam│barato y comprar})\)
\(= \frac{p (\text{barato | spam)} × p (comprar | spam) × p (spam)} {p(barato│spam) × p(comprar|spam) × p(spam) + p(barato|no spam) × p(comprar|no spam) × p(no spam)}\)
\(= \frac{(0,8 × 0,6 × 0,25)} {(0,8 × 0,6 × 0,25)+(0,066 ×0,133 ×0,75)} = 0,94\)
Es decir, según nuestro algoritmo, si un mensaje contiene las palabras «barato» y «comprar» hay un 94% de posibilidades de que sea spam (y 6% de que no lo sea).
Podemos ampliar la lista de palabras incluyendo, por ejemplo, la palabra «trabajo». Obviamente, a medida que añadimos palabras, las probabilidades de que aparezcan todas juntas se van reduciendo, pero es posible calcular la probabilidad de que aparezcan multiplicando las probabilidades de las palabras individuales. Supongamos que la palabra «trabajo» aparece en 5 de los mensajes que son spam y en 30 de los mensajes que no son spam de la muestra).
\(p (\text{trabajo | spam}) = 5/25 = 0,2\)
\(p (\text{trabajo | no spam}) = 30/75 = 0,4\)
Por tanto,
$p () = $
\(= \frac{0,8 × 0,6 × 0,2 × 0,25} {(0,8 × 0,6 × 0,2 × 0,25) + (0,066 × 0,133 × 0,4 × 0,75)} = 0,90\)
En este caso, según nuestro algoritmo, si un mensaje contiene simultáneamente las palabras «barato», «comprar» y «trabajo» hay un 90% de posibilidades de que sea spam —y un 10% de probabilidades de que no lo sea—. La razón de la reducción del porcentaje respecto al caso anterior es que «trabajo» es una palabra asociada a mensajes que no son de spam.
En el capítulo 3 vimos cómo construir un árbol de decisión para clasificar a los clientes de un banco entre posibles morosos y no morosos. A partir de lo que acabamos de ver, ahora podríamos construir un clasificador bayesiano para realizar la misma tarea. Seguidamente, podríamos comparar el rendimiento de ambos algoritmos para determinar cuál es más exitoso. En definitiva, podemos considerar las diferentes técnicas de análisis masivo de datos como una caja de herramientas que podemos emplear para resolver problemas diversos. En cada situación es posible aplicar soluciones diferentes sin que un determinado tipo de problema lleve aparejada necesariamente la utilización de una técnica concreta. En ocasiones el procedimiento a seguir consistirá en probar diferentes soluciones para determinar cuál es la más eficiente, aunque a menudo será difícil determinar porqué un algoritmo funciona mejor que otro. Por utilizar un aforismo del estadístico británico George Box, «All models are wrong, but some are useful.»
4.1 Implementación de un clasificador bayesiano en R
Una escuela de aviación ha recopilado los datos del tiempo de 14 días y la indicación de si en cada uno de ellos se pudo volar o no. La tabla 4.1 presenta los resultados. Con esta información quiere ser capaz de predecir, a partir de la previsión meteorológica, si será posible hacer prácticas de vuelo o no en un día determinado.
| Cielo | Temperatura | Humedad | Viento | Volar |
|---|---|---|---|---|
| sol | calor | alta | suave | no |
| sol | calor | alta | fuerte | no |
| nubes | calor | alta | suave | si |
| lluvia | templado | alta | suave | si |
| lluvia | frio | normal | suave | si |
| lluvia | frio | normal | fuerte | no |
| nubes | frio | normal | fuerte | si |
| sol | templado | alta | suave | no |
| sol | frio | normal | suave | si |
| lluvia | templado | normal | suave | si |
| sol | templado | normal | fuerte | si |
| nubes | templado | alta | fuerte | si |
| nubes | calor | normal | suave | si |
| lluvia | templado | alta | fuerte | no |
Comenzamos instalando y llamando al paquete e1071 que utilizaremos para esta actividad.
library(e1071)Importamos el fichero de datos con la información sobre el tiempo y las condiciones de vuelo. Cambiamos el formato de los datos de «character» a «factor».
vuelo <- read.table("vuelo.txt", header=T, sep = "\t")
library(dplyr)
vuelo <- vuelo%>%mutate_if(is.character, as.factor)El siguiente paso consiste en construir el modelo predictivo utilizando la función naiveBayes. Como argumentos, indicamos la variable que deseamos precedir y el origen de los datos.
VolarModel <- naiveBayes(Volar~., vuelo)Veamos las característica del modelo.
print(VolarModel)##
## Naive Bayes Classifier for Discrete Predictors
##
## Call:
## naiveBayes.default(x = X, y = Y, laplace = laplace)
##
## A-priori probabilities:
## Y
## no si
## 0.3571429 0.6428571
##
## Conditional probabilities:
## Cielo
## Y lluvia nubes sol
## no 0.4000000 0.0000000 0.6000000
## si 0.3333333 0.4444444 0.2222222
##
## Temperatura
## Y calor frio templado
## no 0.4000000 0.2000000 0.4000000
## si 0.2222222 0.3333333 0.4444444
##
## Humedad
## Y alta normal
## no 0.8000000 0.2000000
## si 0.3333333 0.6666667
##
## Viento
## Y fuerte suave
## no 0.6000000 0.4000000
## si 0.3333333 0.6666667Si nos fijamos, simplemente ha calculado la probabilidad global de volar (se pudo volar en 9 de los 14 días, es decir, 0,64) y de no volar (5 días de 14, 0,36), así como la probabilidad de cada uno de los valores de las variables en el modelo en función de que se haya podido volar o no (por ejemplo, la probabilidad de que llueva en un día de vuelo es de 0,33 porque de los 9 días que se ha podido volar, en 3 de ellos llovía).
\(p (\text{sí volar}) = 9/14 = 0,64\)
\(p (\text{no volar}) = 5/14 = 0,36\)
A partir de esta información, dado un nuevo caso, podemos predecir si en esas condiciones se podrá volar o no. Supongamos que la previsión para mañana es de tiempo soleado, temperatura fría, humedad alta y vientos fuertes. Por tanto:
\(p (sí | previsión)=\)
\(\frac{p (sol | sí) × p (frío | sí) × p (alta | sí) × p (fuerte | sí) × p (volar)} {[p (sol | sí) × p (frío | sí) × p (alta | sí) × p (fuerte | sí) × p (volar)] + [p (sol | no) × p (frío | no) × p (alta | no) × p (fuerte | no) × p (no.volar)]}=\)
\(\frac{0,22 × 0,33 × 0,33 × 0,33 × 0,64} {[0,22 × 0,33 × 0,33 × 0,33 × 0,64] + [0,60 × 0,20 × 0,80 × 0,60 × 0,36]}=\)
\(\frac{0,005} {0,005 + 0,020}=0,20\)
Concluimos que los más probable es que no se podrá volar.
Para ver el resultado en R, creamos un objeto con los datos de la previsión.
nuevo_caso <- data.frame(Cielo = "sol",
Temperatura = "frio",
Humedad = "alta",
Viento = "fuerte")Y pedimos al modelo que nos haga una predicción
predict(VolarModel, nuevo_caso)## [1] no
## Levels: no siSi queremos ver los porcentajes
predict(VolarModel, nuevo_caso, type = "raw")## no si
## [1,] 0.7954173 0.2045827Como vemos, la previsión es que no se podrá volar.
4.2 Ejercicio 4. Puntualidad de los trenes
Una compañía ferroviaria ha recogido los siguientes datos sobre la puntualidad de una veintena de trenes. Construye un clasificador bayesiano con RStudio y determina qué es lo más probable que ocurra con un tren que circula un día laborable de invierno con viento fuerte y lluvia intensa (que sea puntual, que llegue tarde, muy tarde o que se cancele).
| dia | estacion | viento | lluvia | puntualidad |
|---|---|---|---|---|
| laborable | primavera | ninguno | ninguna | puntual |
| laborable | invierno | ninguno | debil | puntual |
| laborable | invierno | ninguno | debil | puntual |
| laborable | invierno | fuerte | intensa | tarde |
| sabado | verano | moderado | ninguna | puntual |
| laborable | otono | moderado | ninguna | muy_tarde |
| festivo | verano | fuerte | debil | puntual |
| domingo | verano | moderado | ninguna | puntual |
| laborable | invierno | fuerte | intensa | muy_tarde |
| laborable | verano | ninguno | debil | puntual |
| sabado | primavera | fuerte | intensa | cancelado |
| laborable | verano | fuerte | debil | puntual |
| sabado | invierno | moderado | ninguna | tarde |
| laborable | verano | fuerte | ninguna | puntual |
| laborable | invierno | moderado | intensa | muy_tarde |
| sabado | otono | fuerte | debil | puntual |
| laborable | otono | ninguno | intensa | puntual |
| festivo | verano | moderado | debil | puntual |
| laborable | verano | moderado | ninguna | puntual |
| laborable | verano | moderado | debil | puntual |
La segunda parte del ejercicio es optativa. Hace referencia a los síntomas observados en un grupo de pacientes de un centro de salud y el diagnóstico que se les ha realizado. A partir de la información de la tabla 4.3, construye un clasificador bayesiano con RStudio y determina qué es lo más probable que le ocurra a un nuevo paciente que no tiene fiebre ni diarrea, pero sí vómitos y temblores (no, sí, no, sí). ¿Qué es más probable, que tenga buena salud, gastritis, gripe o salmonela?
| Febre | Vomits | Diarrea | Tremolors | Diagnostic |
|---|---|---|---|---|
| no | no | no | no | saludable |
| mitja | no | no | no | grip |
| alta | no | no | si | grip |
| alta | si | si | no | salmonella |
| mitja | no | si | no | salmonella |
| no | si | si | no | gastritis |
| mitja | si | si | no | gastritis |
| mitja | no | si | no | salmonella |
| no | si | si | no | gastritis |
| mitja | si | si | no | gastritis |
| no | no | no | no | saludable |
| alta | no | no | si | grip |
| alta | si | si | no | salmonella |
| mitja | no | no | no | grip |