Capítulo 5 Regresión
A menudo estamos interesados en describir relaciones entre variables. En el caso de variables cuantitativas, una forma de resumir en un número la fortaleza de esta relación es el coeficiente de correlación de Pearson (r). El coeficiente de correlación describe la dirección —positiva o negativa— y el grado de asociación entre las variables. Su valor oscila entre +1 (correlación positiva perfecta) y –1 (correlación negativa perfecta).
Una forma sencilla de observar de manera visual si existe relación entre dos variables es representarlas en un diagrama de dispersión como los de la Figura 5.1. Si la correlación lineal es perfecta, una línea recta pasará por todos los puntos del diagrama. Si no, es posible construir la línea que mejor se ajuste a las observaciones, aunque no pase por todos los puntos.
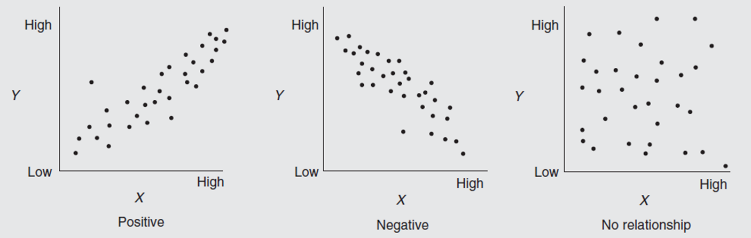
Figure 5.1: Diagramas de dispersión
Relación lineal positiva (r > 0): a media que una variable aumenta también aumenta la otra.
Relación lineal negativa (r < 0): a medida que una variable aumenta, la otra disminuye.
Sin relación lineal (r ≈ 0): las dos variables son independientes.
El coeficiente de correlación simplemente mide la asociación entre dos variables, pero, aunque hablamos de variables independiente y dependiente, no permite afirmar que exista una relación causal entre ambas. Por usar un aforismo habitual en estadística, «la correlación no implica causalidad.»
Veamos un ejemplo. La tabla 5.1 presenta los precios de alquiler de una serie de viviendas según el número de habitaciones de que disponen. ¿Cuánto crees que costará una casa de 4 habitaciones?
| Habitaciones | Alquiler |
|---|---|
| 1 | 150 € |
| 2 | 200 € |
| 3 | 250 € |
| 4 | ¿? |
| 5 | 350 € |
| 6 | 400 € |
La figura 5.2 presenta los mismos datos en forma de un diagrama de dispersión.
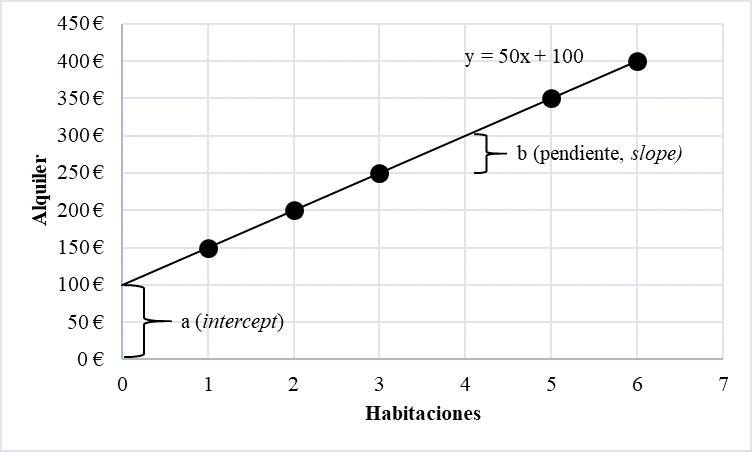
Figure 5.2: Regresión lineal
La regresión es un proceso estadístico para estimar relaciones entre variables, generalmente una o varias variables independientes (o predictoras) y una variable dependiente. Se trata de determinar cómo el valor de la variable dependiente cambia al variar el valor de una de las variables independientes, manteniendo el resto de las variables independientes fijas. La regresión lineal usa la asociación entre dos variables como método de predicción.
Siguiendo con el ejemplo anterior, todos suponemos que el coste de una vivienda de 4 habitaciones es de 300 euros. Intuimos que hay un coste inicial de 100 euros y, a partir de aquí, cada habitación adicional incrementa el alquiler en 50 euros. La ecuación general para una línea de regresión lineal es:
\[Y = a + (b \times X)\]
Y es la variable cuyo valor queremos predecir,
X es la variable independiente o predictora,
a es el punto en que la línea cruza el eje vertical (ordenada en el origen, una constante),
b representa la inclinación de la recta
En el ejemplo, la ecuación de la recta de regresión sería:
\[Y = 100 + (50 \times X)\]
No siempre es posible trazar una línea que pase por todos los puntos, sino que tendremos que buscar una recta que se aproxime el máximo posible a todos ellos. Es habitual utilizar el método de los mínimos cuadrados.
Por otro lado, no todas las regresiones son lineales. La figura 5.3, por ejemplo, muestra la correlación entre el Producto Interior Bruto (PIB) per cápita de una muestra de países y su esperanza de vida. Como se puede observar, la línea que más se acerca a todos los puntos (en color rojo) no es recta. Llega un momento en que, por más rico que sea un país, su esperanza de vida no aumenta.
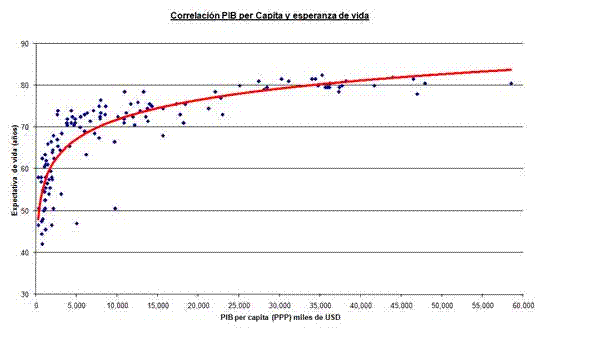
Figure 5.3: Ejemplo de regresión no lineal
Existen diversas extensiones a partir de la idea de la regresión lineal. Así, es posible tener más de una variable predictora (por ejemplo, además del número de habitaciones, considerar el número de baños para calcular el precio del alquiler de una vivienda). En este caso, el diagrama de dispersión será tridimensional y difícil de representar en papel, pero se puede utilizar la misma idea para encontrar la línea que pasa más cerca de todos los puntos. Es lo que se conoce como regresión lineal múltiple en la cual se pondera el valor predictivo de las diversas variables independientes. En este caso, la ecuación de la recta de regresión sería:
\[Y = a + (b_{1} \times X_{1}) + (b_{2} \times X_{2}) + (b_{3} \times X_{3}) + \dotso + (b_{n} \times X_{n})\]
Al igual que antes, a es el punto en que la línea cruza el eje vertical y \(b_{1}\) a \(b_{n}\) son los coeficientes asociados a cada una de las variables independientes.
Por otro lado, no todas las variables son cuantitativas. Hemos visto casos en los que la variable dependiente adopta la forma de categorías que pueden ocurrir o no (por ejemplo, sobrevivir o no al hundimiento del «Titanic»). En este caso debemos recurrir a una regresión logística.
5.1 Regresión lineal en R
Vamos a crear un modelo de regresión lineal en R. Trabajaremos con un pequeño dataset que incluye la edad (en meses), la altura (en centímetros) y el número de hermanos de un grupo de niños y niñas.
| edad | altura | hermanos |
|---|---|---|
| 18 | 76.1 | 1 |
| 19 | 77.0 | 2 |
| 20 | 78.1 | 3 |
| 21 | 78.2 | 2 |
| 22 | 78.8 | 0 |
| 23 | 79.7 | 1 |
| 24 | 79.9 | 5 |
| 25 | 81.1 | 0 |
| 26 | 81.2 | 1 |
| 27 | 81.8 | 4 |
| 28 | 82.8 | 1 |
| 29 | 83.5 | 5 |
Centrándonos en las dos primeras variables, podemos intentar calcular la altura de un niño o niña a partir de su edad utilizando la fórmula:
\[Altura = a + (b × Edad)\]
En este caso, a es la altura de un niño o niña de 0 meses, cuando nace. Por su parte, b es el incremento de altura por cada mes de vida. La regresión en R se calcula utilizando la función lm siguiendo la siguiente sintaxis lm([target] ~ [predictor], data = [data source]). Creamos el modelo y analizamos los resultados:
lmAltura = lm(altura ~ edad, data = edad_altura)
summary(lmAltura)##
## Call:
## lm(formula = altura ~ edad, data = edad_altura)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.27238 -0.24248 -0.02762 0.16014 0.47238
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.9283 0.5084 127.71 < 2e-16 ***
## edad 0.6350 0.0214 29.66 4.43e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.256 on 10 degrees of freedom
## Multiple R-squared: 0.9888, Adjusted R-squared: 0.9876
## F-statistic: 880 on 1 and 10 DF, p-value: 4.428e-11Ya tenemos el valor de a (64,9283) y de b (0,6350). Con estos datos podemos calcular que, por ejemplo, un niño de 20,5 meses medirá:
\[64,9283 + (20,5 × 0,635) = 77,9 \text { cm.}\]
Una regresión lineal puede tener en cuenta dos o más variables independientes o predictoras. Es lo que se conoce como una regresión lineal múltiple. Imaginemos, por ejemplo, que, además de la edad, añadimos una segunda variable para determinar la estatura de los niños: el número de hermanos. La fórmula sería:
\[Altura = a + (b_{1} × Edad) + (b_{2} × Hermanos)\]
El código en R sería el siguiente:
lmAltura2 = lm(altura ~ edad + hermanos, data = edad_altura)
summary(lmAltura2)##
## Call:
## lm(formula = altura ~ edad + hermanos, data = edad_altura)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.26297 -0.22462 -0.02021 0.16102 0.49752
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.90554 0.53526 121.260 8.96e-16 ***
## edad 0.63751 0.02340 27.249 5.85e-10 ***
## hermanos -0.01772 0.04735 -0.374 0.717
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2677 on 9 degrees of freedom
## Multiple R-squared: 0.9889, Adjusted R-squared: 0.9865
## F-statistic: 402.2 on 2 and 9 DF, p-value: 1.576e-09Si tenemos dos niños o niñas con el mismo número de hermanos, el incremento de altura es de 0,63 cm cada mes. De la misma forma, para dos niños o niñas de la misma edad, la estatura decrece en 0,01 cm (observa que el valor es negativo) por cada hermano adicional.
Es fácil pensar que el número de hermanos es una variable poco relevante para determinar la estatura de un niño o niña. Es por ello que hay que fijarse en el p-value de los coeficientes que acabamos de mencionar (a la derecha). El p-value de la edad es 5,85 × e-10, es decir, 0,000000000585. Un valor tan pequeño indica que la edad es buen predictor. En el caso del número de hermanos, el p-value es 0,71. En otras palabras, hay un 71% de probabilidades de que el número de hermanos no sea un predictor significativo. Normalmente, se considera que una variable tiene valor predictivo si el p-value es inferior a 0,05.
Una manera de determinar la bondad del modelo elaborado es fijarse en el coeficiente de determinación \(R^2\) que mide la proporción de la variabilidad explicada por el modelo. Es decir, los modelos con bajo valor predictivo tendrán valores cercanos a 0 y los buenos modelos valores próximos a 1. En nuestro ejemplo, el valor de \(R^2\) es 0,98, lo que nos indica que la edad explica el 98% de la variabilidad en la altura, siempre ciñéndonos a nuestro dataset.
5.2 Ejercicio 5. ¿Qué determina la valoración de un restaurante?
Una web de reseñas de restaurantes publica un dataset que incluye la valoración, para 15 restaurantes, de tres aspectos: comida, ambiente y servicio, así como la puntuación global que recibe de sus clientes. Determina qué variable tiene una mayor correlación con la puntuación global: la comida, el ambiente o el servicio. A continuación, construye un modelo de regresión lineal y determina qué puntuación global obtendrá un restaurante cuya comida obtiene una puntuación de 90, su ambiente de 70 y su servicio de 80.
| restaurante | comida | ambiente | servicio | puntuacion |
|---|---|---|---|---|
| 1 | 85 | 82 | 89 | 78 |
| 2 | 80 | 90 | 80 | 85 |
| 3 | 83 | 86 | 83 | 85 |
| 4 | 70 | 96 | 75 | 72 |
| 5 | 68 | 80 | 78 | 75 |
| 6 | 65 | 70 | 56 | 54 |
| 7 | 64 | 68 | 61 | 62 |
| 8 | 72 | 95 | 72 | 73 |
| 9 | 69 | 70 | 78 | 70 |
| 10 | 75 | 80 | 75 | 77 |
| 11 | 75 | 70 | 75 | 74 |
| 12 | 72 | 90 | 78 | 76 |
| 13 | 81 | 72 | 78 | 80 |
| 14 | 71 | 91 | 71 | 71 |
| 15 | 67 | 86 | 78 | 64 |
La segunda parte del ejercicio es optativa. La tabla 5.4 presenta los datos de audiencia de una veintena de medios de comunicación en su canal tradicional (prensa impresa, televisión, radio, etc.) y en su versión web. Crea un diagrama de dispersión que represente la relación entre ambas variables. A continuación, calcula el coeficiente de correlación de Pearson. Por último, determina la audiencia online de un medio que, en formato tradicional, tiene una audiencia de 2.000.000 de personas.
| Medio | Tradicional | Online |
|---|---|---|
| Marca | 4487000 | 2835000 |
| El País | 4484000 | 1851000 |
| As | 2611000 | 1372000 |
| Antena 3 | 2387000 | 1820000 |
| RTVE | 1855000 | 1718000 |
| La Sexta | 1640000 | 1068000 |
| Sport | 1347000 | 652000 |
| ABC | 1212000 | 577000 |
| La Vanguardia | 1182000 | 748000 |
| Mundo Deportivo | 1122000 | 629000 |
| Europa FM | 1100000 | 1930000 |
| El Periódico | 1057000 | 633000 |
| El Economista | 651000 | 61000 |
| Expansión | 636000 | 171000 |
| La Razón | 631000 | 268000 |
| El Jueves | 615000 | 555000 |
| Onda Cero | 513000 | 2384000 |
| La Voz de Galicia | 503000 | 585000 |
| Kiss FM | 484000 | 884000 |
| Cinco Días | 360000 | 55000 |
Fuente de los datos: Cea-Esteruelas,E. (2016). A comparison of the traditional and online media audiences in Spain. El Profesional de la Información, 25 (3), 351–357.