Capitulo 6 Examen Reglas de asociacion + fcaR
6.1 Ejercicio reglas de asociacion
Dado el dataset con nombre Adult,
Extrae las reglas de asociación con soporte 0.14766 y confianza 0.16254. Guardalas en una variable que se llame mis_reglas. Introduce el número de reglas obtenidas. En el Rmd, hacer un resumen de las reglas obtenidas. Explicar dicho resumen.
¿Qué lift tiene la regla número 3?. Introduce en el cuestionario el valor obtenido.
Ordena las reglas por lift. Muestra la cola (pero solo las últimas 4 reglas) con un solo comando (a poder ser). Muestra por pantalla los atributos de la parte derecha de la última regla que te salga por pantalla de estas 4.
Filtra las reglas obtenidas al principio con valor de estimador de la/el lift mayor que 0.9830694; las guardas en una variable rules2. Ordena estas reglas por support e introduce el valor del estimador support de la primera regla (la más importante teniendo en cuenta este estimador). En el Rmd visualiza las reglas que se te van pidiendo en cada apartado.
Calcula los dos items más frecuentes del dataset. Quédate con las reglas que en la parte izquierda tenga el primer atributo más frecuente y las llamas reglas_de_atributo1. Quédate con las reglas que en la parte derecha tenga el segundo atributo más frecuente y las llamas reglas_de_atributo2. Coge estos dos conjuntos de reglas y realiza la intersección de dichas reglas. Muéstralas por pantalla.
Visualizar con métodos arulesViz en forma matricial las 5 primeras reglas obtenidas en el ejercicio. Introduce el comando en el cuestionario.
Ordenas las reglas extraidas inicialmente por support, selecciona el atributo que está en la derecha de la regla número 2018. Calcula en cuantas transacciones del dataset original está este atributo. Introduce este valor en el cuestionario.
library(arules)
library(arulesViz)
data("Adult")
datos <- Adult
#Extraemos reglas de asociacion
mis_reglas <- apriori(datos, parameter = list(supp = 0.14766, conf = 0.16254, minlen = 2))## Apriori
##
## Parameter specification:
## confidence minval smax arem aval originalSupport maxtime support minlen
## 0.16254 0.1 1 none FALSE TRUE 5 0.14766 2
## maxlen target ext
## 10 rules FALSE
##
## Algorithmic control:
## filter tree heap memopt load sort verbose
## 0.1 TRUE TRUE FALSE TRUE 2 TRUE
##
## Absolute minimum support count: 7212
##
## set item appearances ...[0 item(s)] done [0.00s].
## set transactions ...[115 item(s), 48842 transaction(s)] done [0.03s].
## sorting and recoding items ... [22 item(s)] done [0.00s].
## creating transaction tree ... done [0.02s].
## checking subsets of size 1 2 3 4 5 6 7 8 done [0.01s].
## writing ... [4551 rule(s)] done [0.00s].
## creating S4 object ... done [0.00s].## set of 4551 rules## set of 4551 rules
##
## rule length distribution (lhs + rhs):sizes
## 2 3 4 5 6 7 8
## 238 846 1436 1230 624 161 16
##
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 2.000 4.000 4.000 4.374 5.000 8.000
##
## summary of quality measures:
## support confidence lift count
## Min. :0.1478 Min. :0.1642 Min. :0.7162 Min. : 7217
## 1st Qu.:0.1710 1st Qu.:0.5850 1st Qu.:0.9831 1st Qu.: 8352
## Median :0.1974 Median :0.8719 Median :1.0184 Median : 9640
## Mean :0.2308 Mean :0.7572 Mean :1.1211 Mean :11273
## 3rd Qu.:0.2608 3rd Qu.:0.9284 3rd Qu.:1.0766 3rd Qu.:12737
## Max. :0.8707 Max. :1.0000 Max. :2.6753 Max. :42525
##
## mining info:
## data ntransactions support confidence
## datos 48842 0.14766 0.16254## lhs rhs support confidence
## [1] {relationship=Own-child} => {capital-loss=None} 0.1515499 0.9763883
## lift count
## [1] 1.024243 7402## [1] 1.024243# Ordenar las reglas por lift
mis_reglas_sort <- sort(mis_reglas, by = "lift")
# obtener las ultimas 4
inspect(tail(mis_reglas_sort)[3:6])## lhs rhs support confidence lift count
## [1] {capital-gain=None,
## income=small} => {marital-status=Married-civ-spouse} 0.1598624 0.3296601 0.7194807 7808
## [2] {native-country=United-States,
## income=small} => {marital-status=Married-civ-spouse} 0.1484583 0.3296059 0.7193624 7251
## [3] {capital-gain=None,
## capital-loss=None,
## income=small} => {marital-status=Married-civ-spouse} 0.1542320 0.3283927 0.7167146 7533
## [4] {marital-status=Married-civ-spouse,
## native-country=United-States} => {income=small} 0.1484583 0.3624956 0.7162221 7251## lhs rhs support confidence lift count
## [1] {marital-status=Married-civ-spouse,
## native-country=United-States} => {income=small} 0.1484583 0.3624956 0.7162221 7251## items
## [1] {income=small}# rules2, con lift mayor al especificado, ordenado por support y mostrar dicha regla
rules2 <- subset(mis_reglas, subset = (lift > 0.9830694))
rules2 <- sort(rules2, by = "support")
inspect(rules2[1])## lhs rhs support confidence lift
## [1] {capital-gain=None} => {capital-loss=None} 0.8706646 0.9490705 0.9955863
## count
## [1] 42525## lhs rhs support confidence lift
## [1] {capital-gain=None} => {capital-loss=None} 0.8706646 0.9490705 0.9955863
## count
## [1] 42525## [1] 0.8706646# Acumulamos la frecuencia de los items
itfreq <-itemFrequency(datos)
itfreq <- sort(itfreq, decreasing = TRUE)
# Los dos items mas frecuentes
itfreq[1:2]## capital-loss=None capital-gain=None
## 0.9532779 0.9173867## set of 1431 rules## set of 309 rules## set of 142 rules## lhs rhs support confidence lift count
## [1] {capital-loss=None} => {capital-gain=None} 0.8706646 0.9133376 0.9955863 42525
## [2] {capital-loss=None,
## native-country=United-States} => {capital-gain=None} 0.7793702 0.9117168 0.9938195 38066
## [3] {race=White,
## capital-loss=None} => {capital-gain=None} 0.7404283 0.9099693 0.9919147 36164
## [4] {race=White,
## capital-loss=None,
## native-country=United-States} => {capital-gain=None} 0.6803980 0.9083504 0.9901500 33232
## [5] {workclass=Private,
## capital-loss=None} => {capital-gain=None} 0.6111748 0.9204465 1.0033354 29851
## [6] {workclass=Private,
## capital-loss=None,
## native-country=United-States} => {capital-gain=None} 0.5414807 0.9182030 1.0008898 26447
## [7] {workclass=Private,
## race=White,
## capital-loss=None} => {capital-gain=None} 0.5204742 0.9171628 0.9997559 25421
## [8] {capital-loss=None,
## hours-per-week=Full-time} => {capital-gain=None} 0.5191638 0.9259787 1.0093657 25357
## [9] {workclass=Private,
## race=White,
## capital-loss=None,
## native-country=United-States} => {capital-gain=None} 0.4741616 0.9151223 0.9975317 23159
## [10] {capital-loss=None,
## income=small} => {capital-gain=None} 0.4696573 0.9568282 1.0429934 22939# Visualizacion
# Como las primeras reglas no tienen
# subset <- mis_reglas[1:5]
# plot(subset, method="matrix")
# Un solo comando
plot(mis_reglas[1:5], method="matrix")## Itemsets in Antecedent (LHS)
## [1] "{age=Young}" "{capital-gain=None}"
## [3] "{relationship=Own-child}" "{education=Bachelors}"
## Itemsets in Consequent (RHS)
## [1] "{capital-loss=None}" "{capital-gain=None}"
## [3] "{relationship=Own-child}" "{marital-status=Never-married}"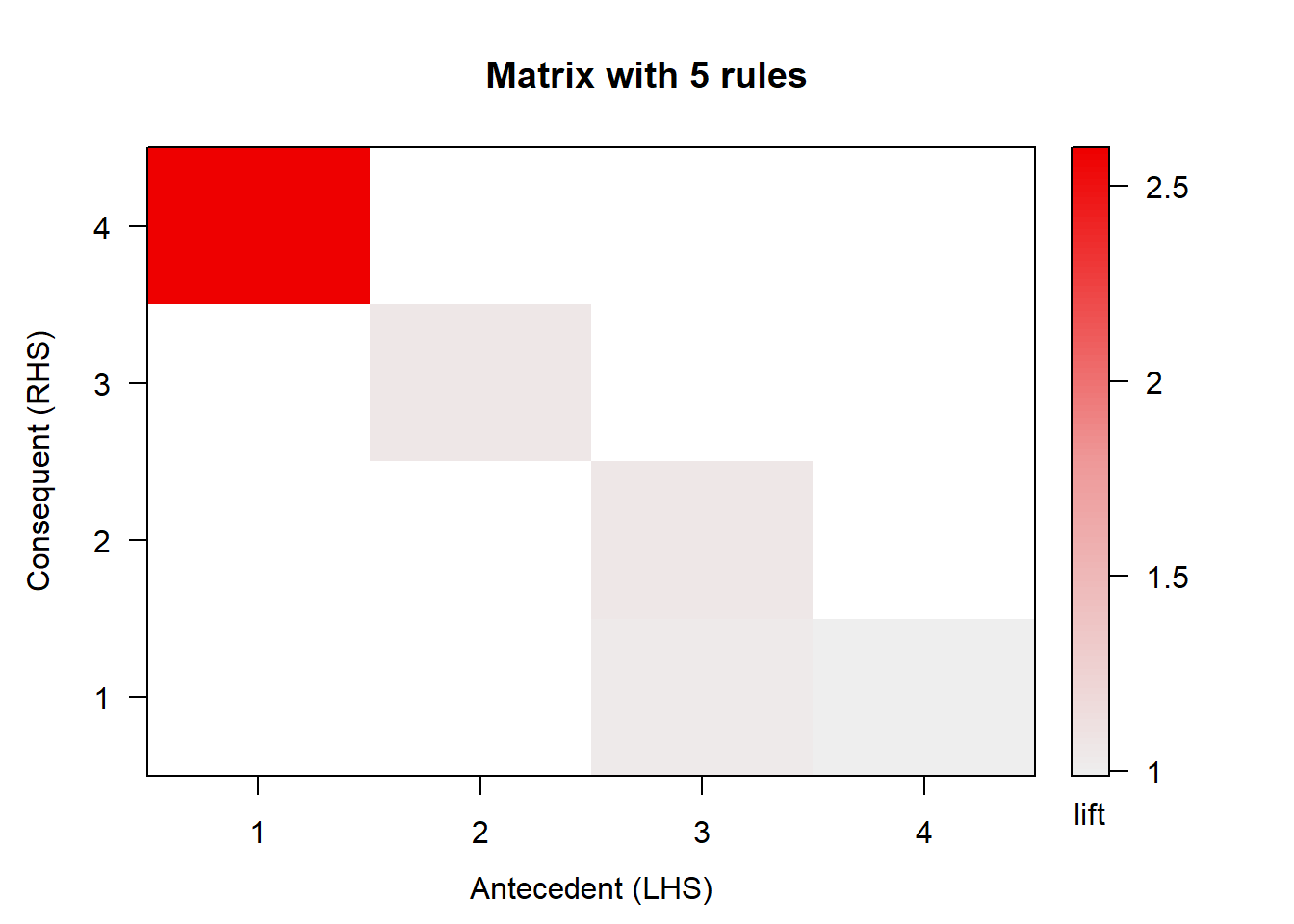
## items
## [1] {native-country=United-States}6.2 Ejercicio fcaR
Descarga de la tarea el fichero random_context.R. Copia el contenido de random_context.R en tu Rmd en un chunk inicial - cuando cargues las librerías necesarias.
Ejecuta FC <- context(num_objetos,num_atributos) donde num_objetos es el valor 35 y num_atributos es el valor 14. Con este comando tendremos un contexto aleatorio para trabajar con él.
Tomando como contexto formal (FC) que acabas de generar, realiza los siguientes apartados en el .Rmd:
Usar método de fcaR para calcular todos los conceptos. Introduce en el cuestionario cuantos conceptos has obtenido. Haz plot del contexto formal. Y dibuja el retículo de conceptos.
Muestra el concepto número 48 por pantalla. Introduce en el cuestionario el soporte de dicho concepto.
¿Es <obj28,att11,att13,att14 un concepto?. Comprobarlo Calcularlo usando los operadores de derivación. No comprobar en la lista de conceptos calculados. Introduce el valor 1 si es un concepto o 0 si no lo es.
Calcula las implicaciones del contexto. ¿Cuantas implicaciones se han extraido?. Introduce en el cuestionario el resultado. Muestra las 10 primeras por pantalla.
Haz una copia (clona) el conjunto original y le das el nombre fc_2. Usando fc_2, aplica todas regla de la lógica de simplificación para eliminiar redundancia. ¿Cuantas implicaciones han aparecido tras aplicar la regla?. Introduce en el cuestionario el resultado.
Extrae de todas las implicaciones la que tengan en el lado izquierda de la implicación el atributo att5. Introduce el número de implicaciones que cumplen esta condición. El programa debe calcularlo. No mirar en todas las implicaciones.
Calcula el soporte de la implicación 32. Introduce este valor en el cuestionario.
library(fcaR)
label.att <- function(n) paste0('att',n)
label.obj <- function(n) paste0('obj',n)
rbv <- function(n) sample(0:1,n,replace = T)
context.no.sparness <- function(num.obj,num.attr) {
mi.df <- data.frame(rbv(num.obj))
for (k in 1:(num.attr-1)){
col <- rbv(num.obj)
mi.df <- cbind(mi.df,col)
}
return(mi.df)
}#End context.no.sparness
#
#' @title Generating a random context
#' @description Algorithm for generate a random context
#' @param num.obj Number of objects for the context
#' @param num.attr Number of attributes for the context
#' @param sparness Probability that an object has an attribute
#' @param namefile Name for the output file
#' @return A data.frame with the random context and a output file
#' @export context
#' @examples
#' c <- context(3, 4, 0.2, "randomContext")
#'
context <- function(num.obj, num.attr, sparness=NULL, namefile="context") {
if (num.obj < 1 || num.attr < 1){
stop("The number of objects and the number of attributes must be greater than zero.")
}
if (!is.null(sparness) && ((sparness < 0) || (sparness > 1))){
stop("Sparness must be a number between 0 and 1.")
}
if(is.null(sparness)){
mi.df <- context.no.sparness(num.obj, num.attr)
}else{
totalN <- num.obj*num.attr
ones <- totalN*sparness
if(ones < totalN/2){
mi.df <- putOnes(mi.df, totalN, ones, num.obj, num.attr)
}else{
mi.df <- putZeros(mi.df, totalN, (totalN-ones), num.obj, num.attr)
}
}
colnames(mi.df) <- as.vector(sapply(1:num.attr,label.att))
rownames(mi.df) <- as.vector(sapply(1:num.obj,label.obj))
# for(k in seq(dim(mi.df)[2])){
# mi.df[,k] <- as.logical(mi.df[,k])
# }
namefile <- paste(namefile, ".csv", sep="")
write.csv(mi.df, file=namefile)
return(mi.df)
}#End context
putOnes <- function(mi.df, totalN, ones, num.obj, num.attr){
bin <- rep(0, totalN)
contI <- 1
contF <- num.obj
mi.df <- data.frame(bin[contI:contF])
for (k in seq(num.attr-1)){
contI <- contI+num.obj
contF <- contF+num.obj
col <- bin[contI:contF]
mi.df <- cbind(mi.df,col)
}
numRow <- 0
numCol <- 0
sum <- 0
while(sum < ones){
numRow <- sample(1:num.obj,1)
numCol <- sample(1:num.attr,1)
if(mi.df[numRow,numCol] == 0){
mi.df[numRow,numCol] <- 1
sum <- sum + 1
}
}
return (mi.df)
}#End putOnes
putZeros <- function(mi.df, totalN, zeros, num.obj, num.attr){
bin <- rep(1, totalN)
contI <- 1
contF <- num.obj
mi.df <- data.frame(bin[contI:contF])
for (k in seq(num.attr-1)){
contI <- contI+num.obj
contF <- contF+num.obj
col <- bin[contI:contF]
mi.df <- cbind(mi.df,col)
}
numRow <- 0
numCol <- 0
sum <- 0
while(sum < zeros){
numRow <- sample(1:num.obj,1)
numCol <- sample(1:num.attr,1)
if(mi.df[numRow,numCol] == 1){
mi.df[numRow,numCol] <- 0
sum <- sum + 1
}
}
return (mi.df)
}#End putZeros
FC <- context(35,14)
fc <- FormalContext$new(FC)
fc$find_concepts()
fc$plot()
# No se si hacer plot de tantos conceptos es lo correcto
# fc$concepts$plot()
# numero
fc$concepts$size()## [1] 522## ({obj13, obj14, obj17, obj19, obj27, obj30, obj32, obj33}, {att8, att12, att13})## [1] 0.2285714# Su derivacion es diferente a la que se nos proporciona
c1 <- SparseSet$new(fc$objects)
c1$assign(obj28 = 1)
fc$intent(c1)## {att2, att4, att5, att9, att10, att11, att14}## [1] 227## Implication set with 10 implications.
## Rule 1: {att11, att13, att14} -> {att8, att12}
## Rule 2: {att11, att12, att14} -> {att8}
## Rule 3: {att11, att12, att13} -> {att8}
## Rule 4: {att10, att11, att12} -> {att8}
## Rule 5: {att9, att11, att14} -> {att10}
## Rule 6: {att9, att10, att12} -> {att8, att13}
## Rule 7: {att8, att11, att14} -> {att12}
## Rule 8: {att8, att10, att13} -> {att12}
## Rule 9: {att8, att10, att12, att13, att14} -> {att9}
## Rule 10: {att8, att10, att11} -> {att12}# Simplificacion
fc2 <- fc$clone()
fc2$implications$apply_rules(rules = "simplification",
parallelize = FALSE)## Processing batch## --> simplification: from 227 to 227 in 0.16 secs.## Batch took 0.16 secs.## [1] 227# fc2$implications
# Extraer del lado izq
imp <- fc2$implications$filter(lhs = "att5")
imp$cardinality()## [1] 59## [1] 0.01694915