Capitulo 3 Lenguaje R

3.1 Ejercicios de Introduccion a R

3.1.1 Ejercicios Introduccion - Vectores I

• Importar el dataset UKgas. Almacenar la columna del dataset en un vector llamado consumo.de.gas. Preparar un fichero .R con las órdenes necesarias para realizar:

library(rmarkdown)
data("UKgas")
consumo.de.gas <- as.vector(UKgas)

• Acceder a los 10 primeros elementos del vector consumo.de.gas

v1 <- consumo.de.gas[1:10]
v1

##  [1] 160.1 129.7  84.8 120.1 160.1 124.9  84.8 116.9 169.7 140.9

• Acceder a los elementos impares del vector consumo.de.gas

v2 <- consumo.de.gas[c(TRUE, FALSE)]
v2

##  [1]  160.1   84.8  160.1   84.8  169.7   89.7  187.3   92.9  176.1   89.7
## [11]  185.7   99.3  200.1  102.5  204.9  112.1  227.3  115.3  244.9  118.5
## [21]  244.9  188.9  301.0  136.1  317.0  152.1  371.4  158.5  449.9  179.3
## [31]  491.5  177.7  593.9  176.1  584.3  187.3  669.2  216.1  827.7  209.7
## [41]  840.5  217.7  848.5  209.7  925.3  214.5  917.3  224.1  989.4  233.7
## [51] 1087.0  281.8 1163.9  347.4

• Acceder a las posiciones 1,4,7,10,… del vector consumo.de.gas

v3 <- consumo.de.gas[c(TRUE, FALSE, FALSE)]
v3

##  [1] 160.1 120.1  84.8 140.9 187.3 120.1  89.7 155.3 200.1 136.1 112.1 195.3
## [13] 244.9 153.7 188.9 196.9 317.0 336.2 158.5 286.6 491.5 409.8 176.1 395.4
## [25] 669.2 509.1 209.7 414.6 848.5 701.2 214.5 515.5 989.4 730.0 281.8 613.1

• Acceder al vector consumo.de.gas en orden inverso

v4 <- consumo.de.gas[length(consumo.de.gas):1]
v4

##   [1]  782.8  347.4  613.1 1163.9  787.6  281.8  534.7 1087.0  730.0  233.7
##  [11]  477.1  989.4  694.8  224.1  515.5  917.3  683.6  214.5  443.4  925.3
##  [21]  701.2  209.7  437.0  848.5  670.8  217.7  414.6  840.5  542.7  209.7
##  [31]  467.5  827.7  509.1  216.1  421.0  669.2  485.1  187.3  395.4  584.3
##  [41]  483.5  176.1  329.8  593.9  409.8  177.7  321.8  491.5  403.4  179.3
##  [51]  286.6  449.9  355.4  158.5  240.1  371.4  336.2  152.1  230.5  317.0
##  [61]  267.3  136.1  196.9  301.0  142.5  188.9  216.1  244.9  153.7  118.5
##  [71]  214.5  244.9  142.5  115.3  195.3  227.3  140.9  112.1  176.1  204.9
##  [81]  136.1  102.5  161.7  200.1  131.3   99.3  155.3  185.7  123.3   89.7
##  [91]  147.3  176.1  120.1   92.9  144.1  187.3  123.3   89.7  140.9  169.7
## [101]  116.9   84.8  124.9  160.1  120.1   84.8  129.7  160.1

• Acceder a los 50 primeros elementos del vector consumo.de.gas excepto la posición 1, 3 y 5.

v5 <- consumo.de.gas[1:50]
v5 <- v5[-(c(1,3,5))]
v5

##  [1] 129.7 120.1 124.9  84.8 116.9 169.7 140.9  89.7 123.3 187.3 144.1  92.9
## [13] 120.1 176.1 147.3  89.7 123.3 185.7 155.3  99.3 131.3 200.1 161.7 102.5
## [25] 136.1 204.9 176.1 112.1 140.9 227.3 195.3 115.3 142.5 244.9 214.5 118.5
## [37] 153.7 244.9 216.1 188.9 142.5 301.0 196.9 136.1 267.3 317.0 230.5

• Sumarle 1 a los elementos del vector consumo.de.gas (reciclaje)

v6 <- consumo.de.gas+1
v6

##   [1]  161.1  130.7   85.8  121.1  161.1  125.9   85.8  117.9  170.7  141.9
##  [11]   90.7  124.3  188.3  145.1   93.9  121.1  177.1  148.3   90.7  124.3
##  [21]  186.7  156.3  100.3  132.3  201.1  162.7  103.5  137.1  205.9  177.1
##  [31]  113.1  141.9  228.3  196.3  116.3  143.5  245.9  215.5  119.5  154.7
##  [41]  245.9  217.1  189.9  143.5  302.0  197.9  137.1  268.3  318.0  231.5
##  [51]  153.1  337.2  372.4  241.1  159.5  356.4  450.9  287.6  180.3  404.4
##  [61]  492.5  322.8  178.7  410.8  594.9  330.8  177.1  484.5  585.3  396.4
##  [71]  188.3  486.1  670.2  422.0  217.1  510.1  828.7  468.5  210.7  543.7
##  [81]  841.5  415.6  218.7  671.8  849.5  438.0  210.7  702.2  926.3  444.4
##  [91]  215.5  684.6  918.3  516.5  225.1  695.8  990.4  478.1  234.7  731.0
## [101] 1088.0  535.7  282.8  788.6 1164.9  614.1  348.4  783.8

• Sumar los 10 primeros elementos del vector consumo.de.gas con el vector v2=(1,2,3)

# Como son tamaños diferentes, cogeré un vector multiplo del vector v2 y luego seleccionare los 10 elementos requeridos
v2 <- c(1,2,3)
v7 <- consumo.de.gas[1:12]
v7 <- v7+v2
v7 <- v7[1:10]
v7

##  [1] 161.1 131.7  87.8 121.1 162.1 127.9  85.8 118.9 172.7 141.9

3.1.2 Ejercicios Funciones

• Programar una función que devuelva dado un vector cuantos números impares tiene. AYUDA: Usar %% para calcular el resto.

n_impares <- function(vector){
  sum <- length(which(vector%%2 != 0))
  return(sum)
}

v1 <- 1:10
n_impares(v1)

## [1] 5

• Programar una función que calcule el volumen de una esfera dado el radio r de dicha esfera. La ecuacion para hallar el volumen de una esfera es \(V = \frac{4}{3}\pi r^3\)

vol_esfera <- function(radio){
  res <- 4/3*pi*radio^3
  return(res)
}
vol_esfera(radio = 2)

## [1] 33.51032

• Programar una función que calcule el volumen de esferas con radio r =1,2,…,20 y devuelva un data.frame con las dos columnas (radio, volumen).

volumenes <- function(vector){
  vols <- vol_esfera(vector)
  return(data.frame("radio"=vector, "volumen"=vols))
}
v <- 1:20
paged_table(volumenes(v))

3.1.3 Manipular Data Frames - Ejercicio 2.1

Importar el dataset HairEyeColor y preparar un fichero .R con los comandos requeridos para lo siguiente:

• Si el dataset importado no es un dataframe convertirlo a dataframe

HairEyeColorDF <- as.data.frame(HairEyeColor)
class(HairEyeColorDF)

## [1] "data.frame"

• Analizar la estructura del dataset, tipo de datos, estructura, clase, etc.

str(HairEyeColorDF)

## 'data.frame':    32 obs. of  4 variables:
##  $ Hair: Factor w/ 4 levels "Black","Brown",..: 1 2 3 4 1 2 3 4 1 2 ...
##  $ Eye : Factor w/ 4 levels "Brown","Blue",..: 1 1 1 1 2 2 2 2 3 3 ...
##  $ Sex : Factor w/ 2 levels "Male","Female": 1 1 1 1 1 1 1 1 1 1 ...
##  $ Freq: num  32 53 10 3 11 50 10 30 10 25 ...

• Obtener número de columnas, número de filas. Guardar en un vector el nombre de las columnas.

dim(HairEyeColorDF)

## [1] 32  4

nrow(HairEyeColorDF)

## [1] 32

ncol(HairEyeColorDF)

## [1] 4

• Cambiar el nombre de la primera columna.

dt2 <- HairEyeColorDF
names(dt2)[1] <- 'Pelo'
paged_table(dt2)

• Averiguar el tipo de datos de la primera columna.

class(dt2[[1]])

## [1] "factor"

• Comando para averiguar si hay valores NA en todo el dataframe, y lo mismo en la columna 1.

as.logical(sum(is.na(HairEyeColorDF)));      #Para todo el dataframe

## [1] FALSE

as.logical(sum(is.na(HairEyeColorDF[, 1]))); # Para la columna 1

## [1] FALSE

• Practicar con el dataset para extraer un conjunto de filas y/o columnas.
• Guardar cinco primeras filas en una variable d1 y las cinco últimas en una variable d2 y combinarlas en un nuevo dataframe llamado d12.

d1 <- HairEyeColorDF[1:5,]
d1

##    Hair   Eye  Sex Freq
## 1 Black Brown Male   32
## 2 Brown Brown Male   53
## 3   Red Brown Male   10
## 4 Blond Brown Male    3
## 5 Black  Blue Male   11

d2 <- HairEyeColorDF[(length(HairEyeColorDF[, 1])-4):length(HairEyeColorDF[,1]), ]
d2

##     Hair   Eye    Sex Freq
## 28 Blond Hazel Female    5
## 29 Black Green Female    2
## 30 Brown Green Female   14
## 31   Red Green Female    7
## 32 Blond Green Female    8

d12 <- rbind(d1,d2)
d12

##     Hair   Eye    Sex Freq
## 1  Black Brown   Male   32
## 2  Brown Brown   Male   53
## 3    Red Brown   Male   10
## 4  Blond Brown   Male    3
## 5  Black  Blue   Male   11
## 28 Blond Hazel Female    5
## 29 Black Green Female    2
## 30 Brown Green Female   14
## 31   Red Green Female    7
## 32 Blond Green Female    8

• Utilizar el comando subset para extraer, eliminar, etc. un conjunto de columnas de un data set.

d3 <- subset(HairEyeColorDF, HairEyeColorDF[4] > 5)
paged_table(d3)

• Usar subset para guardar en una variable las filas de dataset con valor para eye de Blue.

ojos <- subset(HairEyeColorDF, HairEyeColorDF[2] == "Blue")
ojos

##     Hair  Eye    Sex Freq
## 5  Black Blue   Male   11
## 6  Brown Blue   Male   50
## 7    Red Blue   Male   10
## 8  Blond Blue   Male   30
## 21 Black Blue Female    9
## 22 Brown Blue Female   34
## 23   Red Blue Female    7
## 24 Blond Blue Female   64

• Guardar la primera columna en variable d y utilizar los comandos unique, table. ¿Para qué sirven estos comandos?.

d <- HairEyeColorDF[[1]]
d

##  [1] Black Brown Red   Blond Black Brown Red   Blond Black Brown Red   Blond
## [13] Black Brown Red   Blond Black Brown Red   Blond Black Brown Red   Blond
## [25] Black Brown Red   Blond Black Brown Red   Blond
## Levels: Black Brown Red Blond

unique(d)     # Devuelve la estructura sin valores duplicados

## [1] Black Brown Red   Blond
## Levels: Black Brown Red Blond

table(d)      # 'table' utiliza los factores de clasificación cruzada para construir una tabla de contingencia de los recuentos en cada combinación de niveles de factores.

## d
## Black Brown   Red Blond 
##     8     8     8     8

• Con la variable d usar colSums, colMeans. Explicar con ejemplos para qué sirven estos comandos.
• Explicar con ejemplos para qué sirven los comandos rowSums, rowMeans.

# No podemos usar esos comandos con la variable d, pues se trata de una estructura unidimensional
# Usare un data frame compuesto por los valores 1:10 para probar las funciones
df <- data.frame(matrix(1:9,3,3))
df

##   X1 X2 X3
## 1  1  4  7
## 2  2  5  8
## 3  3  6  9

colSums(df)   # Realiza la suma de todos los elementos por columnas

## X1 X2 X3 
##  6 15 24

colMeans(df)  # Realiza la media de todos los elementos por columnas

## X1 X2 X3 
##  2  5  8

rowSums(df)   # Realiza la suma de todos los elementos por filas

## [1] 12 15 18

rowMeans(df)  # Realiza la media de todos los elementos por filas

## [1] 4 5 6

3.1.4 Errores comunes - Ejercicio 2.2

• Explica por qué los siguientes comandos dan error o no hacen lo que podría ser previsible con la lectura del comando. Arreglalo.

# usa mtcars de paquete datasets 
library(datasets) 
data("mtcars") 
mtcars[mtcars$cyl = 4, ]         # La comparacion se realiza con ==
mtcars[-1:4, ]                   # Los indices no estan seleccionados correctamente
mtcars[mtcars$cyl <= 5]          # No se han especificado las columnas
mtcars[mtcars$cyl == 4 | 6, ]    # Se evalua primero 4|6 por lo que siempre será true (suma lógica) y selecciona todos los valores
mtcars[1:20]                     # No se han especificado las columnas
# Errores?? 
x <- 1:5; x[NA]                  # Esta transformando todos los valores en NA

A continuacion se muestra la correccion de los errores

library(datasets)
data("mtcars") 
mtcars[mtcars$cyl == 4, ]                       # Añadimos ==

##                 mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## Datsun 710     22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
## Merc 240D      24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
## Merc 230       22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## Fiat 128       32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
## Honda Civic    30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
## Toyota Corolla 33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
## Toyota Corona  21.5   4 120.1  97 3.70 2.465 20.01  1  0    3    1
## Fiat X1-9      27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
## Porsche 914-2  26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
## Lotus Europa   30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2
## Volvo 142E     21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2

mtcars[1:4, ]                                   # Podemos seleccionar las filas 1:4

##                 mpg cyl disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4      21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag  21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710     22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive 21.4   6  258 110 3.08 3.215 19.44  1  0    3    1

mtcars[-(1:4), ]                                # Podemos eliminar las filas 1:4

##                      mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## Hornet Sportabout   18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
## Valiant             18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
## Duster 360          14.3   8 360.0 245 3.21 3.570 15.84  0  0    3    4
## Merc 240D           24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
## Merc 230            22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## Merc 280            19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
## Merc 280C           17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
## Merc 450SE          16.4   8 275.8 180 3.07 4.070 17.40  0  0    3    3
## Merc 450SL          17.3   8 275.8 180 3.07 3.730 17.60  0  0    3    3
## Merc 450SLC         15.2   8 275.8 180 3.07 3.780 18.00  0  0    3    3
## Cadillac Fleetwood  10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4
## Lincoln Continental 10.4   8 460.0 215 3.00 5.424 17.82  0  0    3    4
## Chrysler Imperial   14.7   8 440.0 230 3.23 5.345 17.42  0  0    3    4
## Fiat 128            32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
## Honda Civic         30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
## Toyota Corolla      33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
## Toyota Corona       21.5   4 120.1  97 3.70 2.465 20.01  1  0    3    1
## Dodge Challenger    15.5   8 318.0 150 2.76 3.520 16.87  0  0    3    2
## AMC Javelin         15.2   8 304.0 150 3.15 3.435 17.30  0  0    3    2
## Camaro Z28          13.3   8 350.0 245 3.73 3.840 15.41  0  0    3    4
## Pontiac Firebird    19.2   8 400.0 175 3.08 3.845 17.05  0  0    3    2
## Fiat X1-9           27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
## Porsche 914-2       26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
## Lotus Europa        30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2
## Ford Pantera L      15.8   8 351.0 264 4.22 3.170 14.50  0  1    5    4
## Ferrari Dino        19.7   6 145.0 175 3.62 2.770 15.50  0  1    5    6
## Maserati Bora       15.0   8 301.0 335 3.54 3.570 14.60  0  1    5    8
## Volvo 142E          21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2

mtcars[mtcars$cyl <= 5, ]                       # Añadimos una coma para seleccionar todas las columnas

##                 mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## Datsun 710     22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
## Merc 240D      24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
## Merc 230       22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## Fiat 128       32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
## Honda Civic    30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
## Toyota Corolla 33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
## Toyota Corona  21.5   4 120.1  97 3.70 2.465 20.01  1  0    3    1
## Fiat X1-9      27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
## Porsche 914-2  26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
## Lotus Europa   30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2
## Volvo 142E     21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2

mtcars[mtcars$cyl == 4 | mtcars$cyl == 6, ]     # Separamos las comparaciones y luego realizamos la operacion OR

##                 mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4      21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag  21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710     22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive 21.4   6 258.0 110 3.08 3.215 19.44  1  0    3    1
## Valiant        18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
## Merc 240D      24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
## Merc 230       22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## Merc 280       19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
## Merc 280C      17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
## Fiat 128       32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
## Honda Civic    30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
## Toyota Corolla 33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
## Toyota Corona  21.5   4 120.1  97 3.70 2.465 20.01  1  0    3    1
## Fiat X1-9      27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
## Porsche 914-2  26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
## Lotus Europa   30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2
## Ferrari Dino   19.7   6 145.0 175 3.62 2.770 15.50  0  1    5    6
## Volvo 142E     21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2

mtcars[1:20, ]                                    # Añadimos una coma para seleccionar todas las columnas

##                      mpg cyl  disp  hp drat    wt  qsec vs am gear carb
## Mazda RX4           21.0   6 160.0 110 3.90 2.620 16.46  0  1    4    4
## Mazda RX4 Wag       21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
## Datsun 710          22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
## Hornet 4 Drive      21.4   6 258.0 110 3.08 3.215 19.44  1  0    3    1
## Hornet Sportabout   18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
## Valiant             18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
## Duster 360          14.3   8 360.0 245 3.21 3.570 15.84  0  0    3    4
## Merc 240D           24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
## Merc 230            22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
## Merc 280            19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
## Merc 280C           17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
## Merc 450SE          16.4   8 275.8 180 3.07 4.070 17.40  0  0    3    3
## Merc 450SL          17.3   8 275.8 180 3.07 3.730 17.60  0  0    3    3
## Merc 450SLC         15.2   8 275.8 180 3.07 3.780 18.00  0  0    3    3
## Cadillac Fleetwood  10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4
## Lincoln Continental 10.4   8 460.0 215 3.00 5.424 17.82  0  0    3    4
## Chrysler Imperial   14.7   8 440.0 230 3.23 5.345 17.42  0  0    3    4
## Fiat 128            32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
## Honda Civic         30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
## Toyota Corolla      33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1

x <- 1:5; x[is.na(x)]                           # Si lo que queremos es consultar los valores nulos usamos is.na

## integer(0)

3.1.5 Vectores y Listas - Ejercicio 2.3

Dado la siguiente pareja de vectores mu y nu, realizar una función que haga lo siguiente:

Vaya cogiendo los elementos de mu y nu que estén en la misma posición y los reuna en vectores.

Todas las parejas se reunirán en una lista y está es la salida de la función.

iset <- function(mu,nu){
  mi.iset <- mapply(c, mu, nu, SIMPLIFY = FALSE)
  return(mi.iset)
}#end function

mu <- c(0.1, 0.3, 1)
nu <- c(0.7, 0.5, 0)
memb <- iset(mu,nu)
str(memb)

## List of 3
##  $ : num [1:2] 0.1 0.7
##  $ : num [1:2] 0.3 0.5
##  $ : num [1:2] 1 0

3.1.6 Vectores y Listas - Ejercicio 2.4

Implementa una función que reciba una matriz y devuelva la diagonal de la matriz D, la submatriz inferior debajo de la diagonal R y la la submatriz superior encima de la diagonal R.

divido.matriz <- function(M){
  return(list(D=diag(M),R=M[upper.tri(M)], L=M[lower.tri(M)])) 
}# fin función

matriz <- matrix(1:9, 3, 3)
divido.matriz(matriz)

## $D
## [1] 1 5 9
## 
## $R
## [1] 4 7 8
## 
## $L
## [1] 2 3 6

3.1.7 Laboratorio C1 - Ejercicio 1

# 1. Crea un vector v1 con los siguientes 10 valores (3, 12, 6, -5, 0, NA, 15, 1, -10, 7).
v1 <- c(3, 12, 6, -5, 0, NA, 15, 1, -10, 7)

# 2. Crea un vector v2 con valores de 0 a 10 de 0.1 en 0.1
v2 <- seq(from = 0, to = 10, by = 0.1)

# 3. Comando para ver el tipo de datos de v1.
class(v1)

## [1] "numeric"

# 4. Resta 2 a los elementos pares de v1 (con una sola orden y de forma vectorial). Define dos funciones que realicen esta tarea.
v1[c(FALSE,TRUE)]-2

## [1] 10 -7 NA -1  5

# 5. Calcula la suma y la media de v2. tem Con los vectores v2 y v3 crea un data.frame de nombre mi.df1.
sumV2 <- sum(v2)
sumV2

## [1] 505

meanV2 <- mean(v2)
meanV2

## [1] 5

v3 <- sin(v2)

mi.df1 <- as.data.frame(cbind(v2,v3))
paged_table(mi.df1)

# 6. Cambia el nombre de columnas de data.frame anterior con las etiquetas x y seno(x).

names(mi.df1) <- c("x", "seno(x)")

# 7. Invierte el orden de los elementos de v2 y lo guardas en v4.
v4 <- v2[(length(v2)):1]
v4

##   [1] 10.0  9.9  9.8  9.7  9.6  9.5  9.4  9.3  9.2  9.1  9.0  8.9  8.8  8.7  8.6
##  [16]  8.5  8.4  8.3  8.2  8.1  8.0  7.9  7.8  7.7  7.6  7.5  7.4  7.3  7.2  7.1
##  [31]  7.0  6.9  6.8  6.7  6.6  6.5  6.4  6.3  6.2  6.1  6.0  5.9  5.8  5.7  5.6
##  [46]  5.5  5.4  5.3  5.2  5.1  5.0  4.9  4.8  4.7  4.6  4.5  4.4  4.3  4.2  4.1
##  [61]  4.0  3.9  3.8  3.7  3.6  3.5  3.4  3.3  3.2  3.1  3.0  2.9  2.8  2.7  2.6
##  [76]  2.5  2.4  2.3  2.2  2.1  2.0  1.9  1.8  1.7  1.6  1.5  1.4  1.3  1.2  1.1
##  [91]  1.0  0.9  0.8  0.7  0.6  0.5  0.4  0.3  0.2  0.1  0.0

# 8. Guarda en un vector v5 los elementos de v1 que no son negativos ni NA.
v5 <- v1[(v1>0) & (!is.na(v1))]
v5

## [1]  3 12  6 15  1  7

# 9. Borra de v1 los elementos negativos.
v1 <- v1[v1 > 0]

# 10. Calcula la longitud de v1 y mira la estructura del vector.
length(v1)

## [1] 7

str(v1)

##  num [1:7] 3 12 6 NA 15 1 7

# 11. Elimina v1 del Workspace de R.
rm(v1)

# 12. Calcula la media de aquellos valores de v2 que sean menores de 1.
media <- mean(v2[v2 < 1])
 
# 13. Elimina de v2 aquellos elementos mayores de 1 y menores de 3.
v2 <- v2[(v2 <= 1)|(v2 >= 3)]

# 14. Calcula la suma acumulada de los valores de v2.
suma <- sum(v2)

# 15. De varias formas distintas crea una matriz M1 con los valores de 1 a 25 con 5 filas (almacenados por filas).
M1 <- matrix(1:25,5,5,byrow = TRUE)      # 1 Forma
M1 <- rbind(1:5,6:10,11:15,16:20,21:25)  # 2 Forma
M1 <- 1:25                               # 3 Forma
dim(M1) <- c(5,5)
M1 <- t(M1)
M1

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    1    2    3    4    5
## [2,]    6    7    8    9   10
## [3,]   11   12   13   14   15
## [4,]   16   17   18   19   20
## [5,]   21   22   23   24   25

# 16. Extrae de la matriz M1 aquellos valores que sean mayores que 10.
M1[M1 > 10]

##  [1] 11 16 21 12 17 22 13 18 23 14 19 24 15 20 25

# 17. Extrae de la matriz M1 la primera y la última columna y guarda el resultado en matriz M2.
M2 <- cbind(M1[,1], M1[,ncol(M1)])

# 18. Calcula el determinante de M1.
det(M1)

## [1] 0

# 19. Calcula la inversa de M1.
# solve(M1) Su determinante es 0, no se puede calcular

# 20. Calcula los autovectores y autovalores de M1. Define una función que dada una matriz devuelvan una lista su radio espectral que se define como el mayor autovalor en módulo y su autovector correspondiente.
eigen(M1)

## eigen() decomposition
## $values
## [1]  6.864208e+01+0.000000e+00i -3.642081e+00+0.000000e+00i
## [3] -2.153465e-15+2.015276e-15i -2.153465e-15-2.015276e-15i
## [5]  7.219523e-16+0.000000e+00i
## 
## $vectors
##               [,1]           [,2]                  [,3]                  [,4]
## [1,] -0.1079750+0i  0.67495283+0i  0.0381046+0.2345472i  0.0381046-0.2345472i
## [2,] -0.2527750+0i  0.36038970+0i  0.2645195-0.2955559i  0.2645195+0.2955559i
## [3,] -0.3975750+0i  0.04582657+0i -0.1224010-0.0257606i -0.1224010+0.0257606i
## [4,] -0.5423751+0i -0.26873656+0i -0.7011750+0.0000000i -0.7011750+0.0000000i
## [5,] -0.6871751+0i -0.58329969+0i  0.5209519+0.0867693i  0.5209519-0.0867693i
##                [,5]
## [1,] -0.11703805+0i
## [2,] -0.22725312+0i
## [3,]  0.82596595+0i
## [4,] -0.50202033+0i
## [5,]  0.02034555+0i

f <- function(m){
  eigens <- eigen(m)
  modulos <- unlist(lapply(eigens$values, Mod))
  indice <- which.max(modulos)
  radEsp <- list(autovalor = (max(modulos[1])), autovector = eigens$vectors[, indice])
  return(radEsp)
}

f(M1)

## $autovalor
## [1] 68.64208
## 
## $autovector
## [1] -0.1079750+0i -0.2527750+0i -0.3975750+0i -0.5423751+0i -0.6871751+0i

3.1.8 Laboratorio C2 - Ejercicio 2

Primero importa el dataset landdata-states.csv del CV

landdata_states <- read.csv("landdata-states.csv")
# 1. Calcula el máximo, mínimo y media de la columna Home.Value.
maximo <- max(landdata_states$Home.Value)
minimo <- min(landdata_states$Home.Value)
media <- mean(landdata_states$Home.Value)

# 2. Elimina la última columna. Elimina la segunda fila del dataset.
landdata_states2 <- landdata_states[, -ncol(landdata_states)]
landdata_states2 <- landdata_states[-2,]

# 3. Explica con ejemplos la diferencia entre usar [] o [[]] para acceder a elementos del data frame. Mira la clase y la estructura de la segunda y tercera columna. Di de que tipo es cada una y su longitud.

# Con [] accedemos a las columnas que indiquemos entre corchetes, pero devuelve un data frame. Si queremos acceder al vector que está dentro del data frame usaremos [[]].
class(landdata_states[[2]])

## [1] "factor"

class(landdata_states[[3]])

## [1] "numeric"

str(landdata_states[[2]])

##  Factor w/ 4 levels "Midwest","N. East",..: 4 4 4 4 4 4 4 4 4 4 ...

str(landdata_states[[3]])

##  num [1:7803] 2010 2010 2010 2010 2008 ...

length(landdata_states[[2]])

## [1] 7803

length(landdata_states[[3]])

## [1] 7803

# 4. De la columna Year cambia todos los años menores del 2000 por NA.
landdata_states$Year[landdata_states$Year < 2000] <- NA

# 5. Cambia - traduciendo el nombre de las columnas del dataset (si alguna columna tiene nombre extraño que no sabemos significado - simplemente coloca primera letra del nombre de inglés y un número).
names(landdata_states) <- c("Estado", "Region", "Fecha", "Valor.Casa", "Estructura.Coste", "Coste.Terreno", "LS1", "Indice.Precio.Casa", "Indice.Precio.Terreno", "Año", "Cuatrimestre")

names(landdata_states)

##  [1] "Estado"                "Region"                "Fecha"                
##  [4] "Valor.Casa"            "Estructura.Coste"      "Coste.Terreno"        
##  [7] "LS1"                   "Indice.Precio.Casa"    "Indice.Precio.Terreno"
## [10] "Año"                   "Cuatrimestre"

paged_table(landdata_states)

3.2 Ejercicios DPLYR

Los siguientes ejercicios se encuentran en el documento dplyr_breast-cancer guion.Rmd del campus.

• Descargar a local desde directorio Datasets de CV, un dataset descargado del repositorio UCI: breast-cancer.data, y breast-cancer.names1.csv (nombres de las columnas)

• Usar el paquete dplyr, otro de los paquetes centrales del denominado tidyverse.

• En tidyverse - dplyr

• Instalar tidyverse

• Cargar paquete tidyverse

library(rmarkdown)
library(dplyr)

3.2.1 Importación de datos

• Importa en R el fichero breast-cancer.data.
• Colocar los nombres al dataset que están en breast-cancer.names1.csv.

cancer <- read.csv("breast-cancer.data", header=FALSE)
nombres <- read.csv("breast-cancer.names1.csv", header=FALSE)
names(cancer) <- nombres[, 1]
names(cancer)  # Comprobamos que se hayan añadido los nombres correctamente

##  [1] "Class"       "age"         "menopause"   "tumor_size"  "inv_nodes"  
##  [6] "node_caps"   "deg_malig"   "breast"      "breast_quad" "irradiat"

3.2.2 dplyr para Manipulación de Datos

Fundamentos de dplyr

5 funciones clave de dplyr:

• Escoger observaciones (filas) según sus valores (filter()).
• Reordenar las filas (arrange()).
• Seleccionar variables por su nombre (select()).
• Crear nuevas variables como función de variables ya existentes (mutate()).
• Encontrar valores representativos de cada variable (summarise()).

Todos estos verbos funcionan de la misma manera:

• El primer argumento es un dataframe.
• Los demás argumentos describen qué hacer con el dataframe, usando los nombres de las variables (columnas) sin necesidad de utilizar comillas.
• El resultado es un nuevo dataframe.

Filtrado de filas con filter()

filter() extrae un subconjunto de las observaciones (filas), basándose en los valores de una o más columnas.

Argumentos: - nombre del dataframe - expresiones (lógicas) para filtrar el dataframe

Ejercicios:

• Extraer las filas del dataset correspondientes al año 1952.
• Extraer las filas del dataset correspondientes al año 1952 y que tienen cancer en el pecho izquierdo.
• Extraer las filas del dataset que tienen cancer en el pecho izquierdo, no radiadas y de edad 40 a 49.

paged_table(cancer %>% 
  filter(breast == "left" & irradiat == "no" & age == "40-49"))

• Reordenar el dataset según el tamaño del tumor.

# Primero reordenare los levels, ya que no se encuentran ordenados por lo que la funcion arrange no realizara una correcta ordenacion.
cancer$tumor_size <- factor(cancer$tumor_size, ordered = TRUE, levels = c("0-4", "5-9", "10-14", "15-19", "20-24", "25-29", "30-34", "35-39", "40-44", "45-49", "50-54"))

paged_table(cancer %>%
  arrange(tumor_size))

• Reordenar el dataset según el tamaño del tumor y el grado que tiene el tumor.

paged_table(cancer %>% 
  arrange(tumor_size, deg_malig))

• Reordenar el dataset según el tamaño del tumor (pero descendiente) y el grado de maligno que tiene el tumor - ayuda - desc(columna).

paged_table(cancer %>% 
  arrange(desc(tumor_size), deg_malig))

• Extraer los 10 pacientes con pre-menopausia, con mayor tamaño de tumor y menor número de nodos invasores y ordenados por edad.

# Al igual que la columna tumor_size, reordenare primero los levels de la columna inv_nodes
cancer$inv_nodes <- factor(cancer$inv_nodes, ordered=TRUE, levels = c("0-2", "3-5", "6-8", "9-11", "12-14", "15-17", "24-26"))

consulta <- cancer %>%
  filter(menopause=="premeno") %>%
  arrange(desc(tumor_size), inv_nodes, age)
  
consulta <- consulta[1:10,]
paged_table(consulta)

top_n()

re-ordenación por una variable y sólo tomar los n valores más altos o más bajos:

• nombre del dataframe,
• n, el número de elementos que recuperar (n negativo los n más bajos)
• el nombre de la variable por la que ordenar

Ejercicios:

• Usando top_n() extraer los 10 pacientes con pre-menopausia, con mayor tamaño de tumor y menor número de nodos invasores y ordenados por edad.

consulta <- cancer %>%
  filter(menopause=="premeno") %>%
  top_n(10, tumor_size) %>%
  top_n(-10, inv_nodes) %>%
  arrange(age)
  
consulta <- consulta[1:10,]
paged_table(consulta)

Selección de columnas select()

• seleccionar únicamente aquellas variables en las que estamos interesados - ayuda - select(dataset, col1, col2, col3)

Ejercicios:

• Seleccionar del dataset las columnas clase, tamaño de tumor y grado de tumor

Podemos seleccionar intervalos de columnas (de col1 a col4):

s1 <- select(dataset, col1:col4)
s1

• ‘deseleccionar’ columnas

select(s1, -c(col1))

Otra utilidad de select(), conjuntamente con la función everything(), es mover algunas columnas o variables al principio del dataframe.

select(dataset, col5, col6, everything())

select()

Otras funciones auxiliares, además del mencionado everything(), que nos pueden ser de ayuda a la hora de seleccionar columnas:

• starts_with('abc'): encuentra todas las columnas cuyo nombre comienza por “abc”.

• ends_with('xyz'): encuentra todas las columnas cuyo nombre termina en “xyz”.

• contains('ijk'): para seleccionar las columnas cuyo nombre contenga la cadena de caracteres “ijk”.

Y otras funciones más complejas (que filtran las columnas por expresiones regulares), que se pueden ver al hacer ?select.

Añadir o renombrar variables con mutate()

El verbo mutate() se usa para añadir nuevas columnas al final del dataframe.

Por ejemplo, añadimos columna dist_grado_peor que es 4.

cancer2 <- mutate(cancer, dist_grado_peor = 4-deg_malig)
cancer2

Ejercicio

• añadir una columna media_tumor que tenga el valor medio de los valores almacenados en variable tumor_size

# Creo una funcion para poder hacer la media del tamaño del tumor.
f <- function(data){
  res <- strsplit(as.character(cancer$tumor_size), "-") # Al ser tipo factor, debo convertirlo en character para separar los valores
  res <- lapply(res, as.integer)                        # convierto a integer los char resultantes
  res <- unlist(lapply(res,mean))                       # Hago la media a cada par y aplano la lista
  return(res)
}

paged_table(cancer %>%
  mutate(media_tumor = f(tumor_size)))

transmute()

Si sólo se desea guardar las nuevas variables, se puede usar la función transmute():

brcan_data <- transmute(brcan_data,
       dist_grado_peor = 4-deg_malig
)

rename()

• función rename(), que, internamente, se comporta como select(), pero guardando todas las variables que no se mencionan explícitamente:

rename(brcan_data, dist_degree_worst = dist_grado_peor)

Uso del operador %>%

• %>% utiliza la salida del término que hay a la izquierda del símbolo %>% como primer argumento de la función que está a la derecha de dicho símbolo.

• x %>% f(y) es igual que hacer f(x, y)

brcan_data %>% 
  filter(breast == "left")

br1 <- brcan_data %>% 
  filter(breast == "left" & age == "30-39") %>% 
  select(deg_malig, tumor_size, everything()) %>% 
  arrange(desc(deg_malig),tumor_size)  
  br1[1:5,]

brcan_data %>% 
  filter(breast == "left" & age == "30-39") %>% 
  top_n(5,desc(deg_malig))

brcan_data %>% 
  filter(breast == "left" & age == "30-39") %>% 
  select(age,tumor_size,deg_malig) %>% 
  top_n(5,desc(deg_malig))

---

3.3 Ejercicios Apply Functions

• Dada la siguiente lista con nombre lista1 que debes introducir en R, resolver los siguientes ejercicios:

lista1 <- list(notas_grupo1 = c(1,2,3,4,5,7,6,5,4,3), notas_grupo2_3 = matrix(c(2,3,2,9,8,8), nrow = 2))
lista1

## $notas_grupo1
##  [1] 1 2 3 4 5 7 6 5 4 3
## 
## $notas_grupo2_3
##      [,1] [,2] [,3]
## [1,]    2    2    8
## [2,]    3    9    8

• Usa lapply() para encontrar la longitud de las notas de todos los grupos que están en lista1.

longitud <- lapply(lista1, length)
longitud

## $notas_grupo1
## [1] 10
## 
## $notas_grupo2_3
## [1] 6

• Usa sapply() para encontrar la media de las notas de todos los grupos que están en lista1.

media <- sapply(lista1, mean)
media

##   notas_grupo1 notas_grupo2_3 
##       4.000000       5.333333

• Usa lapply() para encontrar los quantiles de las notas de todos los grupos que están en lista1.

cuantiles <- lapply(lista1, quantile)
cuantiles

## $notas_grupo1
##   0%  25%  50%  75% 100% 
##    1    3    4    5    7 
## 
## $notas_grupo2_3
##   0%  25%  50%  75% 100% 
## 2.00 2.25 5.50 8.00 9.00

• Dada la siguiente función f1(x)=(3x)/10, aplica f1(x) a todas las notas para cambiar las puntuaciones a la escala de 1 a 3.

f1 <- function(x){
  (3*x)/10
}

result <- lapply(lista1, f1)
result

## $notas_grupo1
##  [1] 0.3 0.6 0.9 1.2 1.5 2.1 1.8 1.5 1.2 0.9
## 
## $notas_grupo2_3
##      [,1] [,2] [,3]
## [1,]  0.6  0.6  2.4
## [2,]  0.9  2.7  2.4

• Repite el ejercicio 4 pero haciendo que f1(x) sea una función anónima dentro de lapply().

result <- lapply(lista1, function(x){(3*x)/10})
result

## $notas_grupo1
##  [1] 0.3 0.6 0.9 1.2 1.5 2.1 1.8 1.5 1.2 0.9
## 
## $notas_grupo2_3
##      [,1] [,2] [,3]
## [1,]  0.6  0.6  2.4
## [2,]  0.9  2.7  2.4

• Encuentra los valores no repetidos de las notas.

diferentes <- apply(lista1[[2]], 1, unique)
diferentes

## [[1]]
## [1] 2 8
## 
## [[2]]
## [1] 3 9 8

d2 <- unlist(diferentes)
d2

## [1] 2 8 3 9 8

lista2 <- list(lista1[[1]], d2)
lista2

## [[1]]
##  [1] 1 2 3 4 5 7 6 5 4 3
## 
## [[2]]
## [1] 2 8 3 9 8

unique(unlist(lista2))

## [1] 1 2 3 4 5 7 6 8 9

• Convierte todas las notas de la lista a un vector (aplana los valores).

# Hacemos uso de unlist y covertimos a vector
vector <- as.vector(unlist(lista1,use.names = FALSE))
vector

##  [1] 1 2 3 4 5 7 6 5 4 3 2 3 2 9 8 8

---

3.4 Visualizacion

Paquetes necesarios

Para poder usar el comando ‘include_graphics’ necesitais que vuestros ordenadores tengan:

• Latex: En Windows instalar MikTeX, en Mac MacTex.
• Pandoc: universal document converter - (https://pandoc.org). Instalar para el S.O. de tu ordenador.

3.4.1 Incrustar gráficos

El siguiente chunk podéis usarlo como plantilla para que sepáis como incrustar gráficos en RMarkdown utilizando el comando ‘include_graphics’ por si os hace falta en algún trabajo. Permite controlar tamaños, etc. Podéis ver en el .Rmd, los parámetros que he puesto en el chunk :

• eval=FALSE. No lo evalua
• echo=TRUE. Si muestra el código en el documento generado.
• fig.width, fig.height, out.width para controlar los tamaños de la salida y del gráfico
• fig.cap: poner una leyenda al gráfico

knitr::include_graphics("ej1.png")
knitr::include_graphics("ej2.png")

3.4.2 Ejercicio 1

Introducir en R el siguiente data frame:

mis.Plantas <- data.frame(Plantas = c("Planta1", "Planta1", "Planta1", "Planta2", 
         "Planta2", "Planta2"),  Tipo = c(1, 2, 3, 1, 2, 3), 
         Eje1 = c(0.2, -0.4, 0.8, -0.2, -0.7, 0.1),  
         Eje2 = c(0.5, 0.3, -0.1, -0.3, -0.1, -0.8))

• Utilizando los comandos básicos de R realizar un gráfico lo más similar posible al que aparece en ModeloDeVisualizacion_ejercicio1_2.html.

# Primer Grafico con 'Plot'
# Defino los colores
colors <- c("#00DCFF", "#007CFF", "#1B00FF")
colors <- colors[mis.Plantas$Tipo]

# Defino las formas
shapes <- c(1,2)
shapes <- shapes[as.numeric(mis.Plantas$Plantas)]

plot(mis.Plantas$Eje1, mis.Plantas$Eje2,
     main = "Sin ggplot", xlab = "Eje 1", ylab = "Eje 2",
     pch = shapes, col = colors
     )
legend("topright", legend = c("Planta 1", "Planta 2"), pch = c(1,2))
legend("bottomright", c("Tipo 1", "Tipo 2", "Tipo 3"), col = c("#00DCFF", "#007CFF", "#1B00FF"), pch = 19)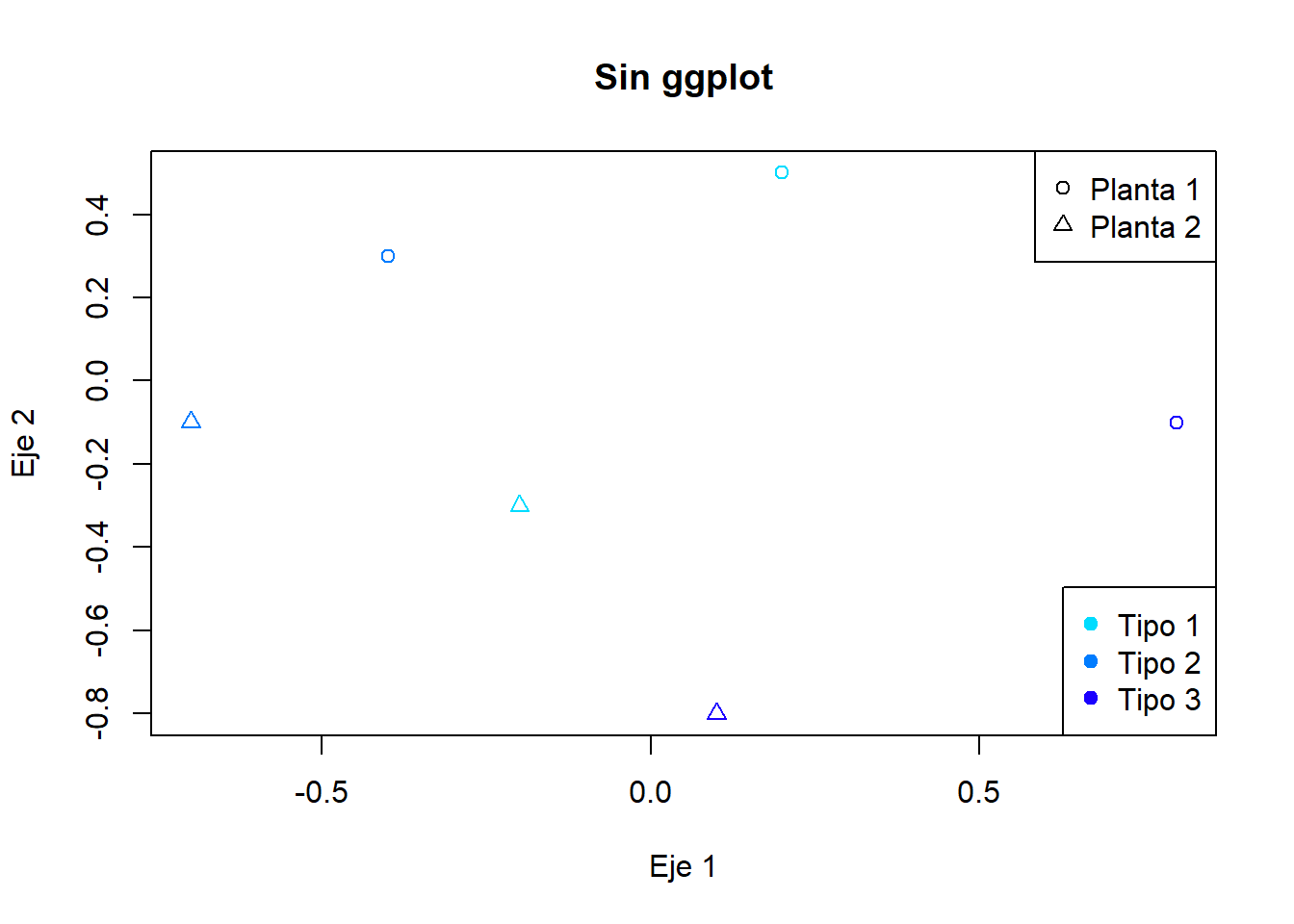

# Segundo grafico con 'ggplot2'
library(ggplot2)
p1 <- ggplot(mis.Plantas, aes(Eje1, Eje2)) +
  ggtitle("Con ggplot") +
  geom_point(aes(color = Tipo, shape = Plantas))
p1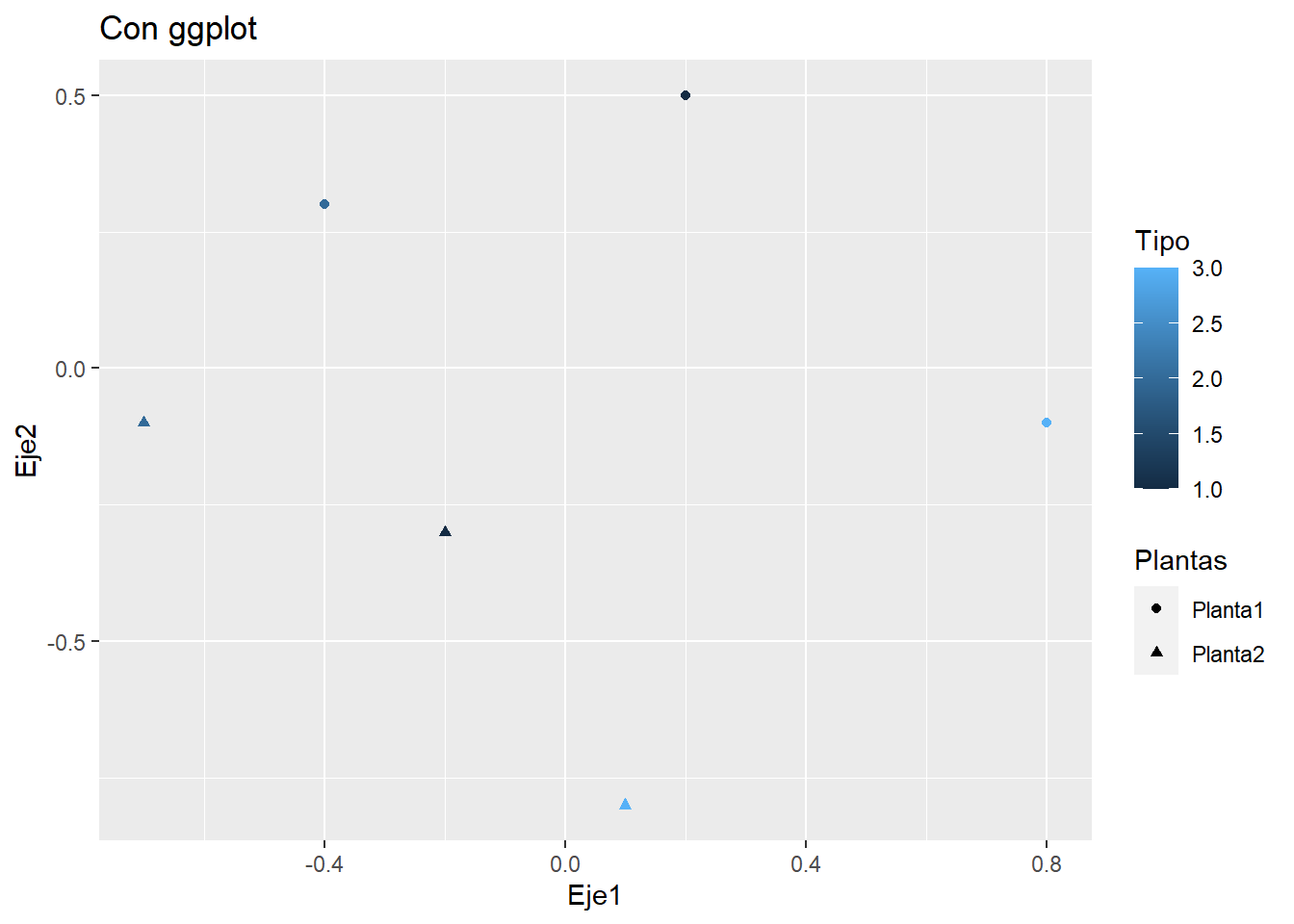

3.4.3 Ejercicio 2

Usaremos el dataset msleep de R (ver las primeras filas del dataset para comprobar la estructura).

• Aplicar ggplot2 para realizar gráficos lo más similares posibles al que aparece en ModeloDeVisualizacion_ejercicio1_2.html.

# Gráfica 3
data("msleep")
sleep <- as.data.frame(msleep)
p2 <- ggplot(sleep, aes(bodywt, sleep_total)) + xlab("Peso de cuerpo") + ylab("Total hora de sueño") +
  ggtitle("Datos de sueño - Gráfico 3") + 
  geom_point()
p2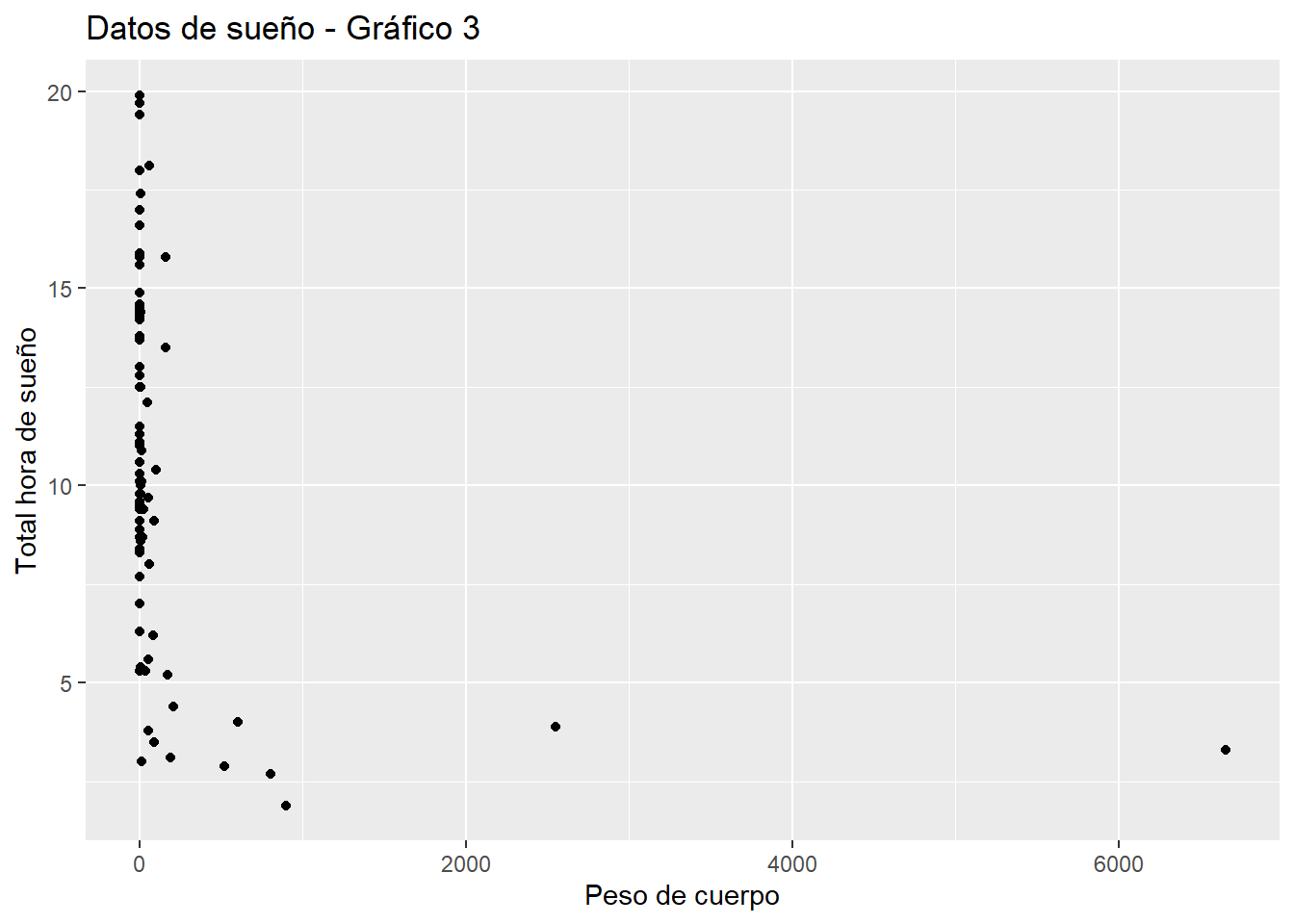

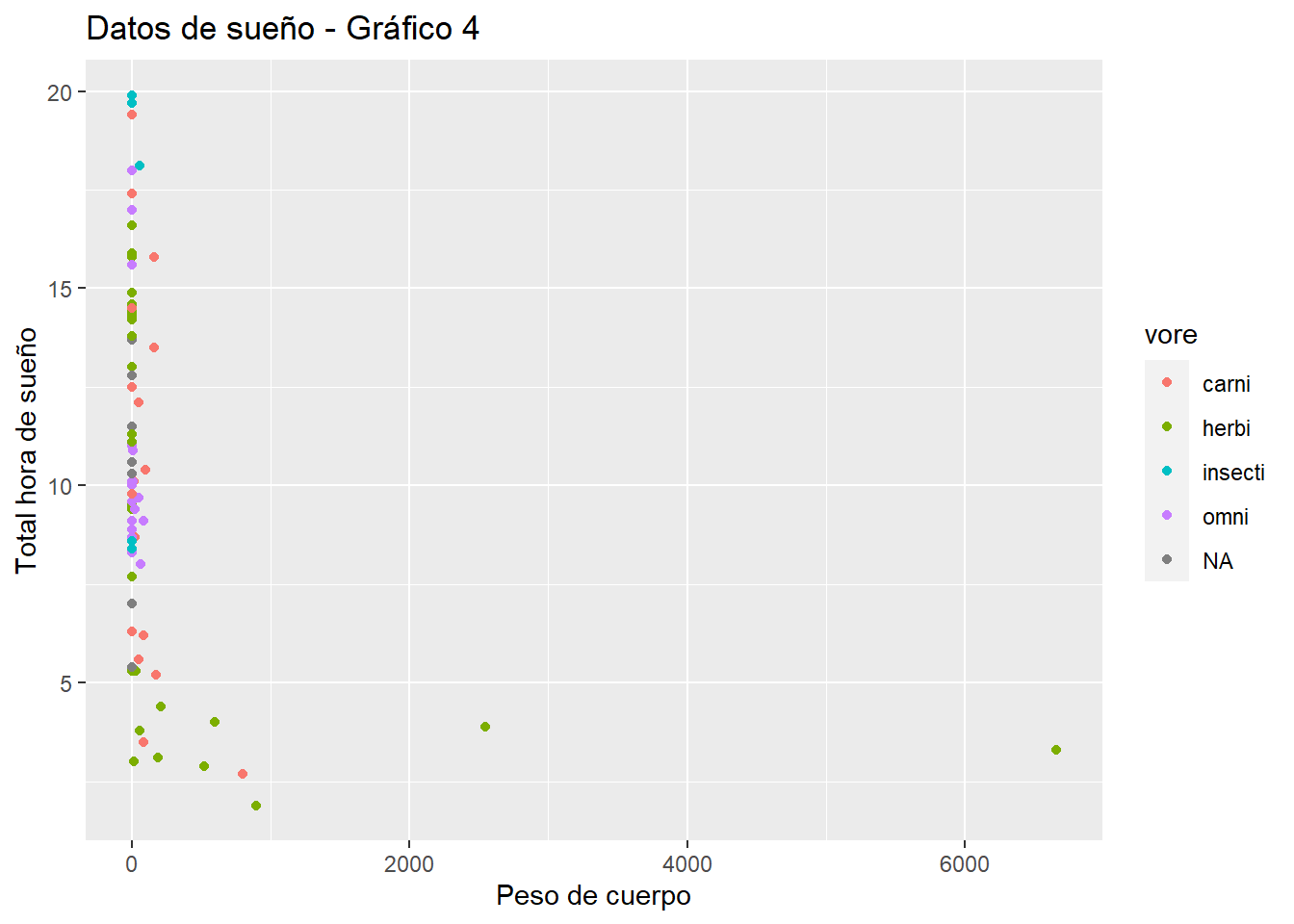
# Gráfica 4
p3 <- p2 + ggtitle("Datos de sueño - Gráfico 4") + geom_point(aes(color = vore))
p3

3.4.4 Ejercicio 3

• Con el mismo dataset del Ejercicio 2, aplicar ggplot2 para realizar gráficos lo más similares posibles al que aparece en ModeloDeVisualizacion_ejercicio3_4.html.

• Ayuda: En el eje X usaremos la función logaritmo, en el eje Y se mostrará la fracción de sueño que es REM respecto al total para cada fila. Modificar posteriormente para la segunda figura.

# Grafica 5
p5 <- ggplot(sleep, aes(log(bodywt), sleep_rem/sleep_total)) + # Habra filas que se eliminan por tener el valor NA
  xlab("Peso de cuerpo") + ylab("Fracción REM respecto al total de horas de sueño") +
  ggtitle("Datos de sueño - Gráfico 5") + 
  geom_point(aes(color = vore))
p5

## Warning: Removed 22 rows containing missing values (geom_point).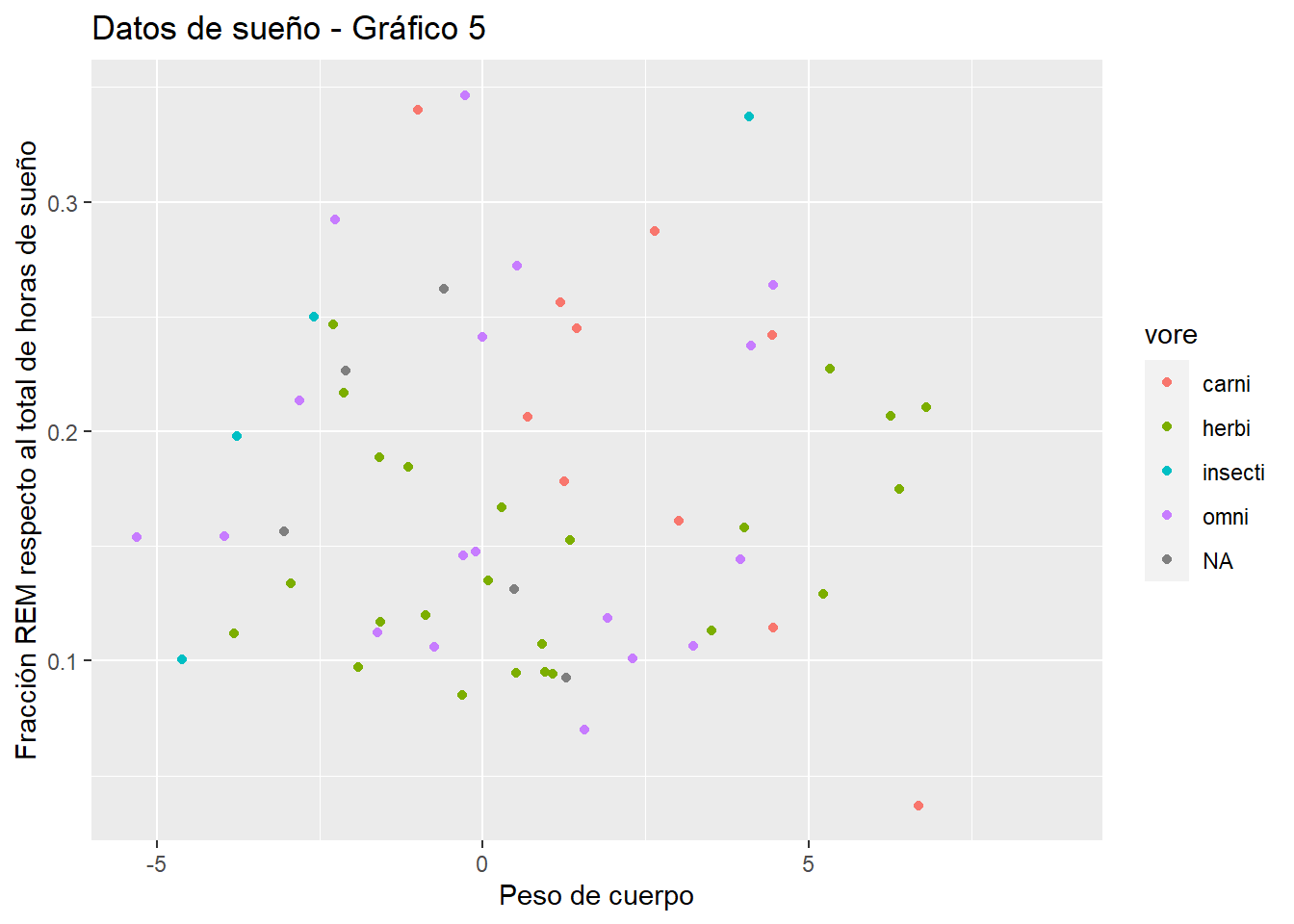

# Grafica 6
p6 <- p5 + ggtitle("Datos de sueño - Gráfico 6") + geom_point(aes(color = vore), size = 4)
p6

## Warning: Removed 22 rows containing missing values (geom_point).

## Warning: Removed 22 rows containing missing values (geom_point).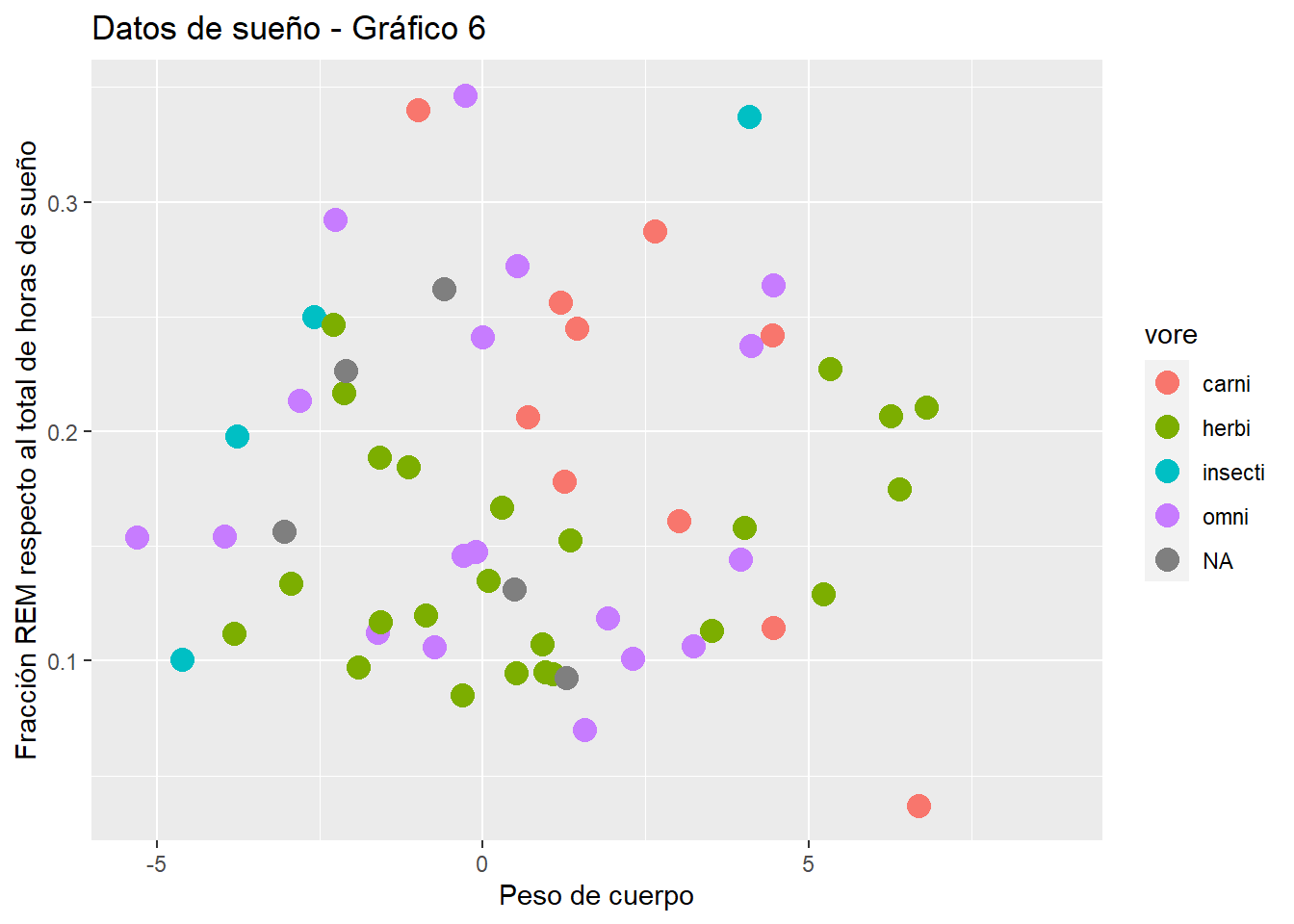

3.4.5 Ejercicio 4

Con el mismo dataset del Ejercicio 2, usar comando facet para dividir los gráficos anteriores en múltiples gráficos.

Realizar gráfico lo más similar posible al que aparece en ModeloDeVisualizacion_ejercicio3_4.html.

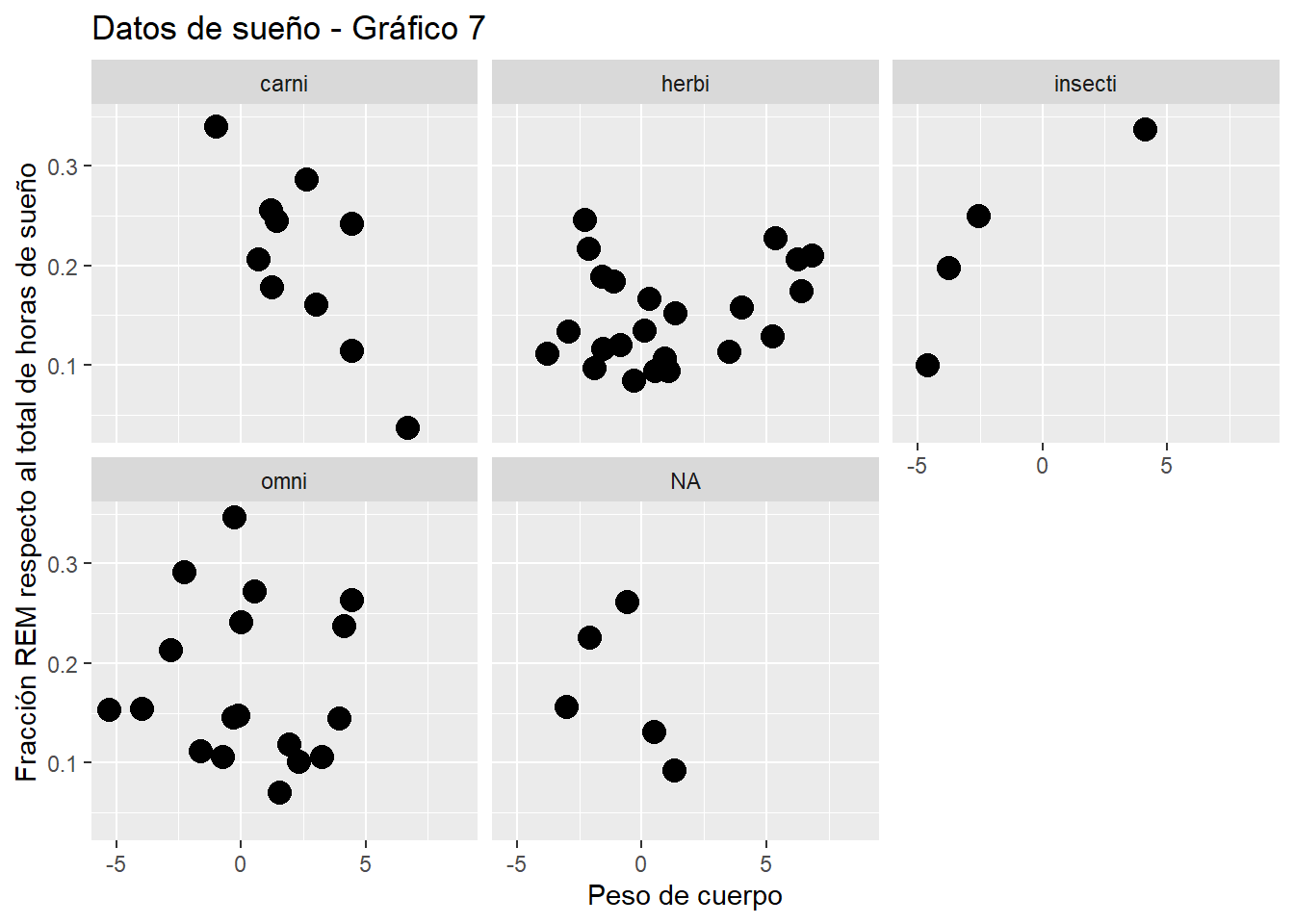
# Grafica 7
p7 <- ggplot(sleep, aes(log(bodywt), sleep_rem/sleep_total)) + # Habra filas que se eliminan por tener el valor NA
  xlab("Peso de cuerpo") + ylab("Fracción REM respecto al total de horas de sueño") +
  ggtitle("Datos de sueño - Gráfico 7") + 
  geom_point(size = 4) + facet_wrap(~sleep$vore)
p7

## Warning: Removed 22 rows containing missing values (geom_point).