Chapter 6 Exploratory Factor Analysis
6.1 Data Import
먼저, 과제에서 사용할 패키지를 불러옵니다.
데이터를 불러옵니다.
# 프로젝트와 동일한 폴더에 들어있는 csv파일을 읽어와서 DATA5에 저장합니다.
data5 <- read.csv("efa_example.csv")
glimpse(data5)## Rows: 299
## Columns: 14
## $ v1 <int> 1, 1, 1, 2, 2, 1, 1, 2, 1, 2, 1, 1, 1, 1, 1, 3, 3, 2, 1, 1, 1, 4, …
## $ v2 <int> 1, 1, 1, 1, 3, 1, 1, 2, 3, 2, 1, 1, 1, 1, 1, 2, 1, 1, 2, 2, 2, 2, …
## $ v3 <int> 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 1, 1, 2, 1, 2, 1, 2, 2, 1, 1, 2, …
## $ v4 <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 1, …
## $ v5 <int> 1, 1, 1, 2, 1, 2, 3, 2, 1, 1, 2, 2, 2, 1, 2, 1, 2, 1, 1, 2, 1, 1, …
## $ v6 <int> 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
## $ v7 <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 1, 2, 1, 1, 1, 1, 1, …
## $ v8 <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
## $ v9 <int> 2, 3, 3, 1, 1, 2, 1, 1, 1, 1, 1, 2, 1, 2, 1, 2, 1, 1, 3, 1, 3, 2, …
## $ v10 <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, …
## $ v11 <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 3, 1, 1, 2, 1, 1, 1, 1, …
## $ v12 <int> 1, 1, 1, 1, 1, 3, 1, 1, 1, 1, 2, 2, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, …
## $ v13 <int> 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 1, 2, 2, 1, 1, 1, 1, …
## $ v14 <int> 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 2, 2, 1, 1, 1, 1, 2, 1, 2, 2, 1, …- 데이터를 보면, v1 ~ v14까지 총 14개의 variable로 구성되어 있습니다.
- 과제에서 요구하는 질문은 다음과 같이 총 4가지 입니다.
1. efa_example.csv 파일을 사용하여 탐색적요인분석(EFA)을 다음의 절차에 맞게 분석하라.
1-1. 본 데이터는 요인분석을 실시하기에 적합한 데이터인가? (2가지 방법 모두를 활용)
1-2. 본 데이터는 몇 가지 요인을 추출하는 것이 적절한가? (3가지 방법 모두를 활용)
1-3. 1-2의 결과를 바탕으로 최대우도를 사용하여 탐색적 요인분석을 실시하고 그 결과를 보고하라.
1-4. fa.diagram()을 사용하여 1-3의 결과를 제목은 EFA Results이고 factor 간의 상관관계가 모두 표현된 plot으로 표현하라.6.2 요인분석 적절성 판단
- 요인분석을 실시하는 것이 의미가 있는지 파악하기 위해
Bartlett의 구형성 검정과 KMO검정, 두 가지 검정을 실시합니다.
6.2.1 Bartlett의 구형성 검정
변수간 상관계수 행렬의 행렬식 값을 계산하여,
단위행렬에 대항하는지 아닌지 카이제곱 분포를 활용하여 검증합니다.상관계수가 대각행렬일 경우, 변수들간 상관관계가 없기 때문에
요인분석을 하기에 적절하지 않다는 것을 의미합니다.Bartlett의 구형성 검정은 p value가 .05 이하인 경우,
변수가 대각행렬이 아니라는 뜻으로 요인분석에 적합하다는 뜻입니다.변수의 상관관계 matrix를 cortest.bartlett 함수에 넣어 검증합니다.
# 1. Bartlett 구형성 검증을 위한 샘플사이즈 계산
data5 %>% nrow() # 299개, n이 30개 이상이므로 CLT에 의해 정규성을 띈다 가정하고 진행## [1] 299data5 %>%
cor() %>%
cortest.bartlett(n = 299) %>%
as.data.frame() %>%
knitr::kable(digits = c(2, 0, 1), caption = c("Bartlett의 구형성 검증 결과"), format = "html", align = "ccc")| chisq | p.value | df |
|---|---|---|
| 1148.87 | 0 | 91 |
Bartlett의 구형성 검증 결과, p value가 0.00으로 유의하므로, 요인분석을 하기에 적절합니다.
Bartlett Test의 경우, 데이터의 비정규성에 매우 민감하며, 유의한 상관이 없더라도
유의한 결과를 제공하는 경향이 있기에 n=30 이하인 경우에는 cor.mtest()함수를
사용하여 변수간 상관관계를 살펴보는 것이 좋습니다.
6.2.2 KMO 검정
- Kaiser-Meyer-Olkin 검정은 변수들간 상관관계가 다른 변수들에 의해 잘 설명되는지 여부를 알려줍니다.
- KMO값이 .5 이상이 되어야 설명력이 있다고 보며, 기준은 아래와 같습니다.
| KMO값 | 기준 |
|---|---|
| 0.9 이상 | 좋음 |
| 0.8 이상 | 양호 |
| 0.6~0.7 | 보통 |
| 0.5 이하 | 부적절 |
- KMO 검정을 실시합니다.
data5 %>% KMO()## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = .)
## Overall MSA = 0.75
## MSA for each item =
## v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 v11 v12 v13 v14
## 0.73 0.70 0.71 0.76 0.72 0.77 0.79 0.75 0.62 0.69 0.87 0.83 0.80 0.75- KMO 값 기준은 아래와 같고, 모두 0.6 이상이므로 요인분석에 적합하다고 볼 수 있습니다.
6.2.3 요인분석 적절성 판단 결과
- Bartlett의 구형성 검정과 KMO검정 실시 결과, efa_example 데이터는
요인분석에 적합한 것으로 확인되었습니다.
1. efa_example.csv 파일을 사용하여 탐색적요인분석(EFA)을 다음의 절차에 맞게 분석하라.
1-1. 본 데이터는 요인분석을 실시하기에 적합한 데이터인가?
(2가지 방법 모두를 활용)
-> 두 가지 방법으로 분석 결과 적합한 것으로 확인됨6.3 요인추출
- efa_example 데이터로부터 몇개의 요인을 추출하는 것이 적합한지 확인하기 위해
Kaiser’s rule, Scree test, *Parallel analysis 방법을 활용하겠습니다.
6.3.1 Kaiser’s Rule
Kaiser’s Rule은 상관행렬의 eigen value이 1보다 큰 것의 개수를 구해
해당 값을 요인의 개수로 결정합니다.하지만, 표본이 작은 경우 요인 수를 과대평가하는 경향이 있어서,
최근에는 참고용으로만 보고 있습니다.
pacman::p_load(nFactors)
# Kaiser's Rule with scree plot
data5 %>%
cor() %>%
scree(pc = FALSE, main = c(" Scree plot for efa_example data"), hline = 1)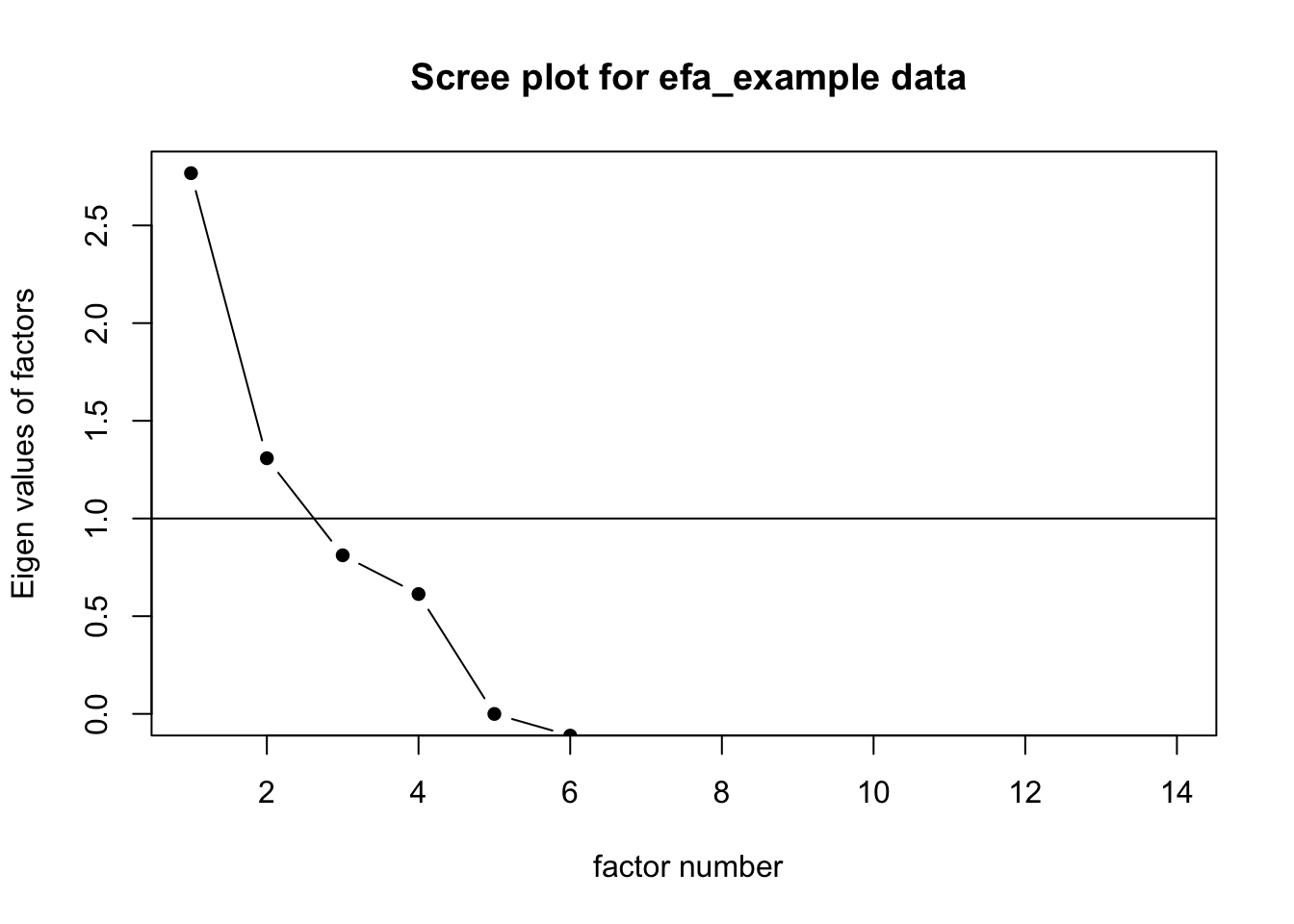
- Scree plot으로 eigen value가 1을 넘는 요인의 수를 간단하게 확인하실 수 있습니다.
- eigen value가 1보다 큰 요인의 수가 2개임을 알 수 있습니다.
# Kaiser's Rule with eigen value table
data5 %>% eigenComputes(model = "factors") -> eigenTable
eigenTable %>%
as.data.frame() %>%
mutate(factor_number = c(1:14))## . factor_number
## 1 2.891881952 1
## 2 1.534475036 2
## 3 0.959932562 3
## 4 0.855368932 4
## 5 0.105713004 5
## 6 0.004064692 6
## 7 0.003397895 7
## 8 -0.071110194 8
## 9 -0.101914687 9
## 10 -0.120464827 10
## 11 -0.183663813 11
## 12 -0.205283859 12
## 13 -0.231170886 13
## 14 -0.266734908 14주성분 분석과 다르게, 탐색적 요인분석의 경우,
reduced correlation matrix로 eigen value를 계산해야 합니다.eigenComputes함수를 활용하여 요인분석의 eigen value를 계산하면,
Scree plot과 동일하게 eigen value가 1 이상인 요인은 2개 입니다.
6.3.2 Scree plot
- Scree plot은 새로운 차원(요인 수)을 추가할 경우, 설명분산을 유의미하게 증가시키지 않으면 요인을 포함하지 않는 방법입니다.
바꿔 말하면, eigen value 곡선에서 변곡점을 찾아내고, 해당 변곡점을 요인의 수로 결정하는 방법입니다.
# Scree plot
data5 %>%
cor() %>%
scree(pc = FALSE, main = c(" Scree plot for efa_example data"), hline = -1)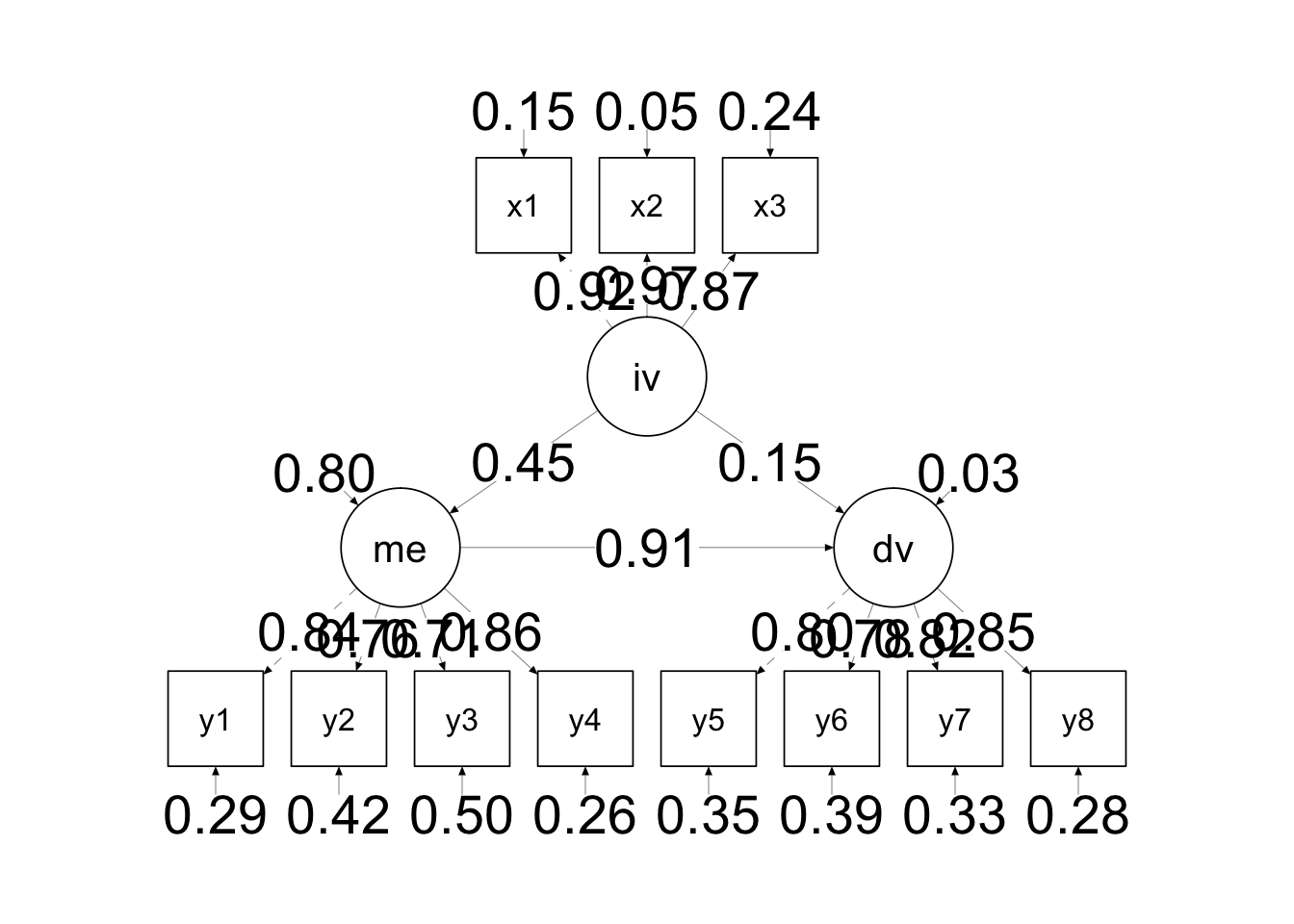
Scree Plot을 통해 확인해보면, 요인이 1개인 경우와 4개인 경우가 변곡점인 것 같습니다.
정확한 판단을 위해 요인분석을 하면서 누적분산비율을 보기도 하는데,
우선 다음 분석으로 넘어가 보겠습니다.
6.3.3 Parallel Analysis
- 마지막으로 평행분석을 진행합니다.
평행분석기법은 표본상관계수 행렬의 크기와 동일한 무선 상관행렬을 생성한 다음
eigen value를 계산하고 평균 eigen value보다 큰 eigen value의 개수로 요인의 수를 추정합니다.
-이 기법은 표집의 오차를 고려하는 방법 이기 때문에
앞서 진행했던 Kaiser’s Rule보다는 더 논리적인 방법입니다.
data5 %>% paran(iterations = 5000, cfa = TRUE, graph = TRUE, all=TRUE)##
## Using eigendecomposition of correlation matrix.
## Computing: 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
##
##
## Results of Horn's Parallel Analysis for factor retention
## 5000 iterations, using the mean estimate
##
## --------------------------------------------------
## Factor Adjusted Unadjusted Estimated
## Eigenvalue Eigenvalue Bias
## --------------------------------------------------
## No components passed.
## --------------------------------------------------
## 1 2.458816 2.891881 0.433065
## 2 1.196926 1.534475 0.337548
## 3 0.694034 0.959932 0.265898
## 4 0.651108 0.855368 0.204260
## 5 -0.042707 0.105713 0.148420
## 6 -0.092946 0.004064 0.097010
## 7 -0.045230 0.003397 0.048628
## 8 -0.073293 -0.07111 0.002183
## 9 -0.059646 -0.10191 -0.04226
## 10 -0.035009 -0.12046 -0.08545
## 11 -0.054469 -0.18366 -0.12919
## 12 -0.032379 -0.20528 -0.17290
## 13 -0.010479 -0.23117 -0.22069
## 14 0.009683 -0.26673 -0.27641
## --------------------------------------------------
##
## Adjusted eigenvalues > 0 indicate dimensions to retain.
## (4 factors retained)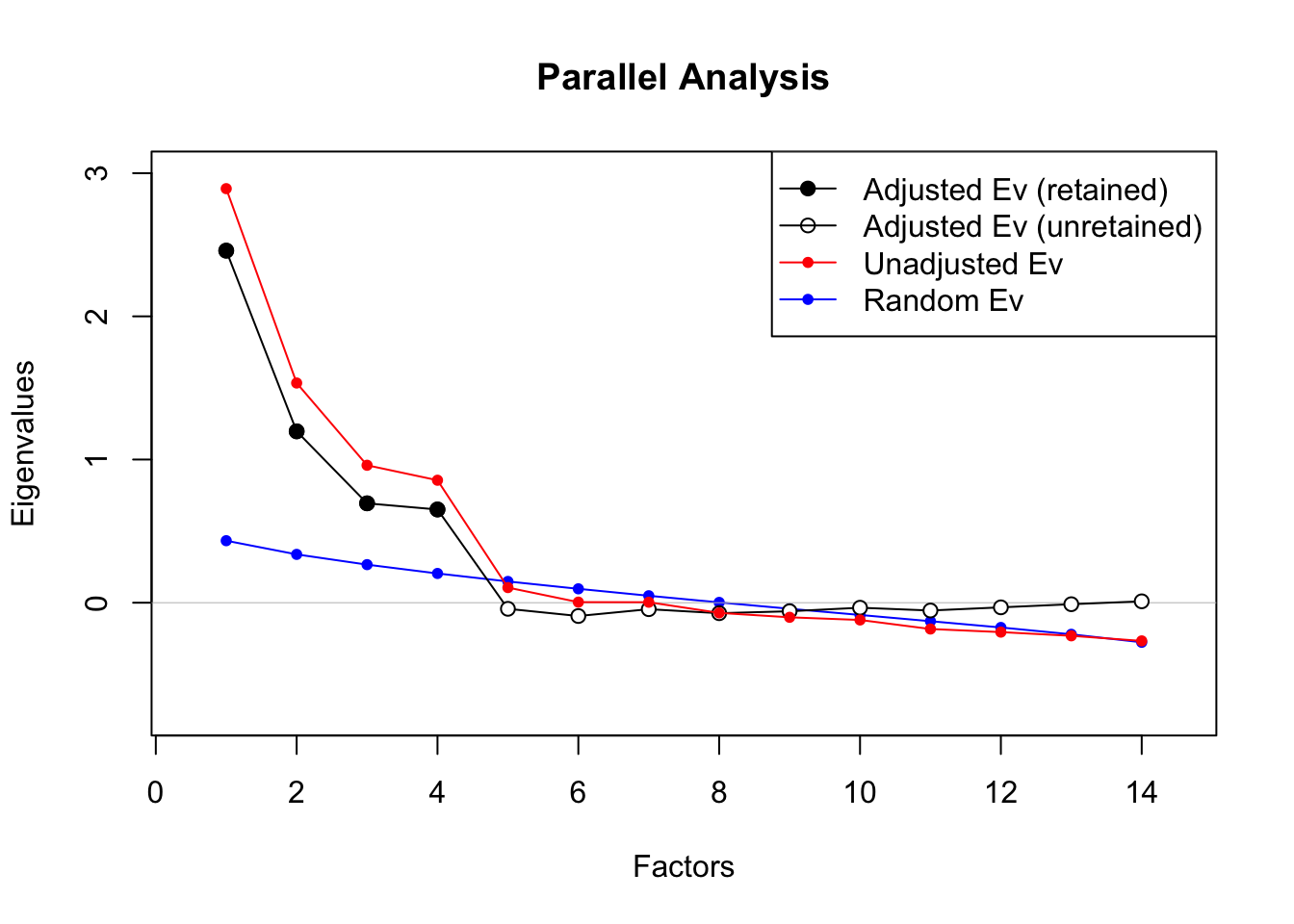
- 평행분석 결과, Random Sampling에 의한 EV인 파란색 선보다 위에 있는
Adjusted Ev가 4개임을 확인할 수 있으며, 4 factors retained라고 출력된 것을 확인할 수 있습니다.
6.3.4 추가 방법(1)
nFactors 라이브러리의 nScree, plotnScree 함수를 사용하면,
Kaiser’s Rule과 Parallel Analysis, Optimal Coordinate, Acceleration Factor,
총 네가지 방법에 의한 적절한 요인의 수를 계산해줍니다.nScree 함수의 경우, default model이 주성분분석인 components로 되어 있으므로,
반드시 factors로 지정해주셔야 제대로 요인분석을 하실 수 있습니다.nScree에서는 Raiche et al.,(2006)의 Acceleration Factor 와 Optimal Coordinates 에 의한 요인 개수 추정값도 보여줍니다. Acceleration Factor 방법은 곡선의 기울기가 가장 급격하게 변하는 요인 개수를 추정하며,
Optimal Coordinates는 eigen value의 이전 값과 현재 값의 기울기를 기반으로 요인 개수를 추정합니다.
# eigen value 계산
data5 %>% eigenComputes(model = "factors") -> ev
# parallel analysis
parallel(subject = nrow(data5), var = ncol(data5), rep = 100, quantile = .95, model = "factors") -> ap
# nScree 통해 Vairous Scree Test
nScree(x = ev, aparallel = ap$eigen$qevpea, model = "factors") %>%
plotnScree(main = c("Various Scree Test for efa_example"))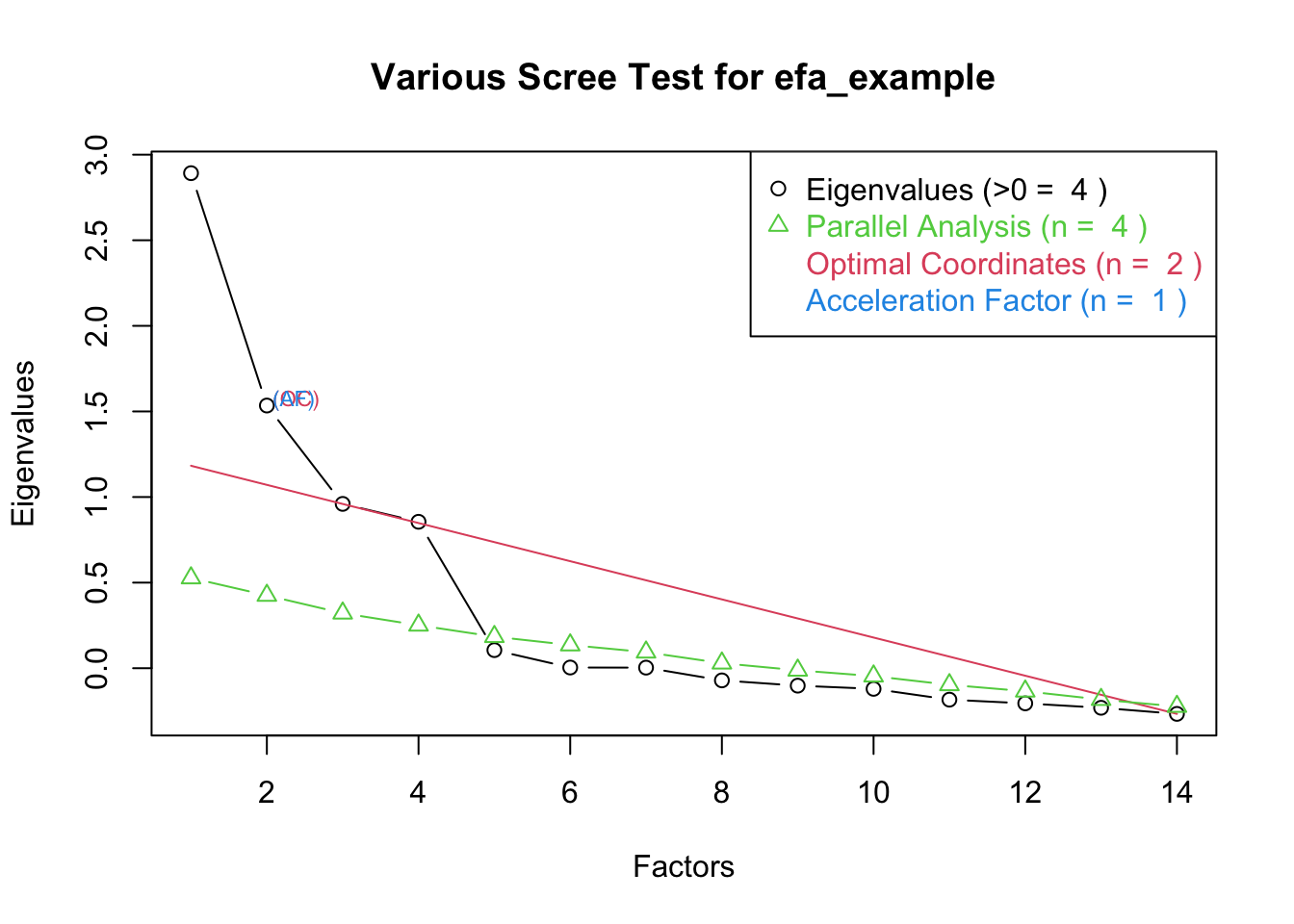
- nFactors package에 의한 결과는 앞서 했던 것과 동일하게 나왔으며, OC에 의해서는 2개, AF에 의해서는 1개를 추천해주고 있습니다.
6.3.5 추가 방법(2)
- 이번엔 psych 패키지에 내장되어 있는 평행분석 함수를 사용해보겠습니다.
data5 %>% fa.parallel(n.iter = 1000, fa = "fa", fm = "ml", plot = TRUE)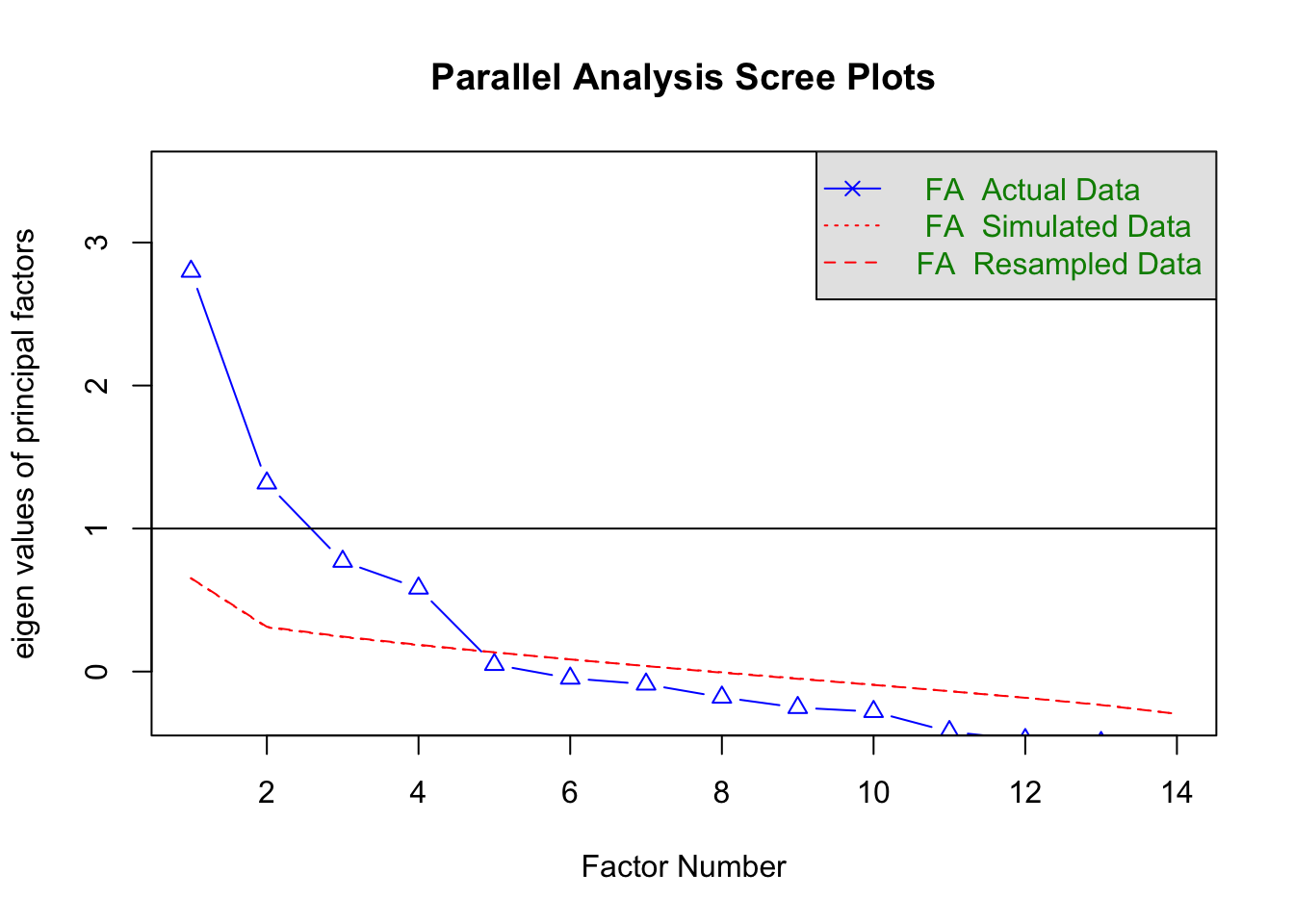
## Parallel analysis suggests that the number of factors = 4 and the number of components = NA- 누적 분산비율을 확인하고 싶을 때는, fa()함수나 factanl()함수를 활용하면 됩니다.
fa와 factanal은 둘다 탐색적 요인분석을 위한 함수이지만,
factanal은 Maximum likelihood 방법만을 활용하며, fa는 Ordinary least square regression 과
같은 방법도 활용할 수 있습니다.
fa(data5, nfactors = 4, fm = "ml", rotate = "promax")%>%print## Factor Analysis using method = ml
## Call: fa(r = data5, nfactors = 4, rotate = "promax", fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
## ML1 ML3 ML4 ML2 h2 u2 com
## v1 0.00 0.09 0.63 -0.13 0.40 0.60 1.1
## v2 0.00 -0.08 0.76 -0.04 0.54 0.46 1.0
## v3 -0.01 -0.05 0.67 0.17 0.53 0.47 1.1
## v4 -0.02 0.47 0.05 0.13 0.28 0.72 1.2
## v5 -0.01 0.65 -0.16 -0.06 0.38 0.62 1.1
## v6 0.00 0.74 0.07 -0.03 0.57 0.43 1.0
## v7 0.07 0.71 0.06 -0.04 0.56 0.44 1.0
## v8 -0.05 0.12 -0.01 0.50 0.28 0.72 1.1
## v9 0.00 -0.13 -0.09 0.71 0.46 0.54 1.1
## v10 0.08 0.00 0.09 0.76 0.65 0.35 1.1
## v11 0.58 0.03 -0.03 0.02 0.34 0.66 1.0
## v12 0.70 -0.03 0.02 0.05 0.49 0.51 1.0
## v13 0.76 -0.02 0.04 -0.07 0.57 0.43 1.0
## v14 0.82 0.04 -0.05 0.01 0.69 0.31 1.0
##
## ML1 ML3 ML4 ML2
## SS loadings 2.11 1.73 1.49 1.40
## Proportion Var 0.15 0.12 0.11 0.10
## Cumulative Var 0.15 0.27 0.38 0.48
## Proportion Explained 0.31 0.26 0.22 0.21
## Cumulative Proportion 0.31 0.57 0.79 1.00
##
## With factor correlations of
## ML1 ML3 ML4 ML2
## ML1 1.00 0.41 0.17 0.05
## ML3 0.41 1.00 0.24 0.22
## ML4 0.17 0.24 1.00 0.27
## ML2 0.05 0.22 0.27 1.00
##
## Mean item complexity = 1.1
## Test of the hypothesis that 4 factors are sufficient.
##
## The degrees of freedom for the null model are 91 and the objective function was 3.93 with Chi Square of 1148.87
## The degrees of freedom for the model are 41 and the objective function was 0.2
##
## The root mean square of the residuals (RMSR) is 0.03
## The df corrected root mean square of the residuals is 0.04
##
## The harmonic number of observations is 299 with the empirical chi square 34.14 with prob < 0.77
## The total number of observations was 299 with Likelihood Chi Square = 56.64 with prob < 0.053
##
## Tucker Lewis Index of factoring reliability = 0.967
## RMSEA index = 0.036 and the 90 % confidence intervals are 0 0.057
## BIC = -177.08
## Fit based upon off diagonal values = 0.99
## Measures of factor score adequacy
## ML1 ML3 ML4 ML2
## Correlation of (regression) scores with factors 0.92 0.89 0.87 0.87
## Multiple R square of scores with factors 0.84 0.79 0.76 0.76
## Minimum correlation of possible factor scores 0.68 0.57 0.51 0.52factanal(data5, rotation = 'promax', factors = 4)##
## Call:
## factanal(x = data5, factors = 4, rotation = "promax")
##
## Uniquenesses:
## v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 v11 v12 v13
## 0.597 0.461 0.470 0.724 0.619 0.434 0.442 0.722 0.541 0.351 0.656 0.508 0.429
## v14
## 0.310
##
## Loadings:
## Factor1 Factor2 Factor3 Factor4
## v1 0.124 0.618 -0.112
## v2 0.748
## v3 0.666 0.187
## v4 0.476 0.135
## v5 0.644 -0.182
## v6 0.750
## v7 0.715
## v8 0.117 0.496
## v9 -0.130 0.706
## v10 0.768
## v11 0.573
## v12 0.699
## v13 0.756
## v14 0.818
##
## Factor1 Factor2 Factor3 Factor4
## SS loadings 2.071 1.766 1.445 1.412
## Proportion Var 0.148 0.126 0.103 0.101
## Cumulative Var 0.148 0.274 0.377 0.478
##
## Factor Correlations:
## Factor1 Factor2 Factor3 Factor4
## Factor1 1.0000 -0.0523 0.406 -0.154
## Factor2 -0.0523 1.0000 -0.228 0.243
## Factor3 0.4058 -0.2279 1.000 -0.224
## Factor4 -0.1544 0.2425 -0.224 1.000
##
## Test of the hypothesis that 4 factors are sufficient.
## The chi square statistic is 56.64 on 41 degrees of freedom.
## The p-value is 0.0528- 앞서 진행했던 것과 마찬가지로 prallel analysis를 통해 4개의 요인을 추출해줍니다.
1-2. 본 데이터는 몇 가지 요인을 추출하는 것이 적절한가? (3가지 방법 모두를 활용)
-> parallel 분석 결과, 4개의 요인을 추출하는 것이 적절한 것으로 보입니다. 6.4 EFA(ML)
1-3. 1-2의 결과를 바탕으로 최대우도를 사용하여 탐색적 요인분석을 실시하고 그 결과를 보고하라.- 이제 4개 요인으로 EFA 를 진행해보겠습니다.
6.4.1 Mardia’s test
ML은 다변량 정규분포를 가정하고 진행하는 방법이기에 다변량 정규성 가정을 충족하는지
Mardia’s test를 진행해보겠습니다.Mardia’s test는 MVN패키지의 mvn()함수로 확인하실 수 있습니다.
library(MVN)## Registered S3 method overwritten by 'GGally':
## method from
## +.gg ggplot2## sROC 0.1-2 loadedmvn(data5,mvnTest ="mardia")## $multivariateNormality
## Test Statistic p value Result
## 1 Mardia Skewness 1050.15474600308 2.84348330414713e-32 NO
## 2 Mardia Kurtosis 7.99445729064163 1.33226762955019e-15 NO
## 3 MVN <NA> <NA> NO
##
## $univariateNormality
## Test Variable Statistic p value Normality
## 1 Shapiro-Wilk v1 0.8667 <0.001 NO
## 2 Shapiro-Wilk v2 0.8765 <0.001 NO
## 3 Shapiro-Wilk v3 0.8761 <0.001 NO
## 4 Shapiro-Wilk v4 0.8338 <0.001 NO
## 5 Shapiro-Wilk v5 0.8148 <0.001 NO
## 6 Shapiro-Wilk v6 0.7829 <0.001 NO
## 7 Shapiro-Wilk v7 0.7156 <0.001 NO
## 8 Shapiro-Wilk v8 0.6886 <0.001 NO
## 9 Shapiro-Wilk v9 0.8850 <0.001 NO
## 10 Shapiro-Wilk v10 0.8535 <0.001 NO
## 11 Shapiro-Wilk v11 0.7127 <0.001 NO
## 12 Shapiro-Wilk v12 0.8624 <0.001 NO
## 13 Shapiro-Wilk v13 0.8326 <0.001 NO
## 14 Shapiro-Wilk v14 0.8304 <0.001 NO
##
## $Descriptives
## n Mean Std.Dev Median Min Max 25th 75th Skew Kurtosis
## v1 299 2.314381 0.8363555 2 1 5 2 3.0 0.04637994 -0.5032636
## v2 299 2.498328 0.8722977 2 1 4 2 3.0 0.00510207 -0.6969371
## v3 299 2.501672 0.9099546 3 1 4 2 3.0 -0.11147207 -0.8104620
## v4 299 1.926421 0.8560508 2 1 4 1 2.5 0.52418934 -0.5971154
## v5 299 1.882943 0.7438856 2 1 4 1 2.0 0.58001549 0.1107384
## v6 299 1.712375 0.6981861 2 1 4 1 2.0 0.69239819 0.1656159
## v7 299 1.515050 0.6520033 1 1 4 1 2.0 1.10292414 0.9791819
## v8 299 1.494983 0.7252458 1 1 4 1 2.0 1.35881437 1.1921259
## v9 299 2.448161 1.0712009 2 1 5 2 3.0 0.10161450 -1.0621436
## v10 299 2.063545 0.8857421 2 1 4 1 3.0 0.33860739 -0.8077635
## v11 299 1.538462 0.7380086 1 1 4 1 2.0 1.26578494 1.0343536
## v12 299 2.163880 0.9249885 2 1 4 1 3.0 0.40708549 -0.6857645
## v13 299 1.949833 0.9452238 2 1 5 1 3.0 0.76476180 -0.1269546
## v14 299 1.929766 0.8660740 2 1 4 1 2.0 0.66001637 -0.2751217- 분석결과 다변량 정규성을 만족하지 못하는 것으로 나왔기에,
다변량 정규분포에 민감한 최대우도법을 사용해서는 안되지만,
과제의 조건에 맞춰 최대우도법을 활용하여 탐색적 요인분석을 진행해보겠습니다.
6.4.2 탐색적 요인분석
data5 %>%
fa(nfactors = 4, fm = "ml", rotate = "promax") %>%
summary()##
## Factor analysis with Call: fa(r = ., nfactors = 4, rotate = "promax", fm = "ml")
##
## Test of the hypothesis that 4 factors are sufficient.
## The degrees of freedom for the model is 41 and the objective function was 0.2
## The number of observations was 299 with Chi Square = 56.64 with prob < 0.053
##
## The root mean square of the residuals (RMSA) is 0.03
## The df corrected root mean square of the residuals is 0.04
##
## Tucker Lewis Index of factoring reliability = 0.967
## RMSEA index = 0.036 and the 10 % confidence intervals are 0 0.057
## BIC = -177.08
## With factor correlations of
## ML1 ML3 ML4 ML2
## ML1 1.00 0.41 0.17 0.05
## ML3 0.41 1.00 0.24 0.22
## ML4 0.17 0.24 1.00 0.27
## ML2 0.05 0.22 0.27 1.00- 표본의 크기에 따른 최소 factor loading 값은 아래와 같습니다.
| 표본의 크기 | 최소 요인 적재 값 |
|---|---|
| 50 | .75 |
| 100 | .55 |
| 150 | .45 |
| 200 | .40 |
| 250 | .35 |
| 350 | .30 |
이번 과제의 표본은 n=299이므로, 최소 .35만 넘으면 됩니다.
4개의 요인으로 잘 묶였는지 factor loading값 기준으로 살펴보면,
아래와 같이 네개의 요인으로 묶이는 것을 확인할 수 있습니다.- ML1: V11, V12, V13, V14
- ML2: V8, V9, V10
- ML3: V4, V5, V6, V7
- ML4: V1, V2, V3
data5 %>% fa(nfactors = 4, fm = "ml", rotate = "promax") -> fa5
fa5 %>% print.psych(sort = TRUE)## Factor Analysis using method = ml
## Call: fa(r = ., nfactors = 4, rotate = "promax", fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
## item ML1 ML3 ML4 ML2 h2 u2 com
## v14 14 0.82 0.04 -0.05 0.01 0.69 0.31 1.0
## v13 13 0.76 -0.02 0.04 -0.07 0.57 0.43 1.0
## v12 12 0.70 -0.03 0.02 0.05 0.49 0.51 1.0
## v11 11 0.58 0.03 -0.03 0.02 0.34 0.66 1.0
## v6 6 0.00 0.74 0.07 -0.03 0.57 0.43 1.0
## v7 7 0.07 0.71 0.06 -0.04 0.56 0.44 1.0
## v5 5 -0.01 0.65 -0.16 -0.06 0.38 0.62 1.1
## v4 4 -0.02 0.47 0.05 0.13 0.28 0.72 1.2
## v2 2 0.00 -0.08 0.76 -0.04 0.54 0.46 1.0
## v3 3 -0.01 -0.05 0.67 0.17 0.53 0.47 1.1
## v1 1 0.00 0.09 0.63 -0.13 0.40 0.60 1.1
## v10 10 0.08 0.00 0.09 0.76 0.65 0.35 1.1
## v9 9 0.00 -0.13 -0.09 0.71 0.46 0.54 1.1
## v8 8 -0.05 0.12 -0.01 0.50 0.28 0.72 1.1
##
## ML1 ML3 ML4 ML2
## SS loadings 2.11 1.73 1.49 1.40
## Proportion Var 0.15 0.12 0.11 0.10
## Cumulative Var 0.15 0.27 0.38 0.48
## Proportion Explained 0.31 0.26 0.22 0.21
## Cumulative Proportion 0.31 0.57 0.79 1.00
##
## With factor correlations of
## ML1 ML3 ML4 ML2
## ML1 1.00 0.41 0.17 0.05
## ML3 0.41 1.00 0.24 0.22
## ML4 0.17 0.24 1.00 0.27
## ML2 0.05 0.22 0.27 1.00
##
## Mean item complexity = 1.1
## Test of the hypothesis that 4 factors are sufficient.
##
## The degrees of freedom for the null model are 91 and the objective function was 3.93 with Chi Square of 1148.87
## The degrees of freedom for the model are 41 and the objective function was 0.2
##
## The root mean square of the residuals (RMSR) is 0.03
## The df corrected root mean square of the residuals is 0.04
##
## The harmonic number of observations is 299 with the empirical chi square 34.14 with prob < 0.77
## The total number of observations was 299 with Likelihood Chi Square = 56.64 with prob < 0.053
##
## Tucker Lewis Index of factoring reliability = 0.967
## RMSEA index = 0.036 and the 90 % confidence intervals are 0 0.057
## BIC = -177.08
## Fit based upon off diagonal values = 0.99
## Measures of factor score adequacy
## ML1 ML3 ML4 ML2
## Correlation of (regression) scores with factors 0.92 0.89 0.87 0.87
## Multiple R square of scores with factors 0.84 0.79 0.76 0.76
## Minimum correlation of possible factor scores 0.68 0.57 0.51 0.526.5 EFA(ML) Plot
1-4. fa.diagram()을 사용하여 1-3의 결과를 제목은 EFA Results이고 factor 간의 상관관계가 모두 표현된 plot으로 표현하라.data5 %>%
fa(nfactors = 4, fm = "ml", rotate = "promax") %>%
fa.diagram(digits = 3, errors = FALSE, main = "EFA Results", cut = .35)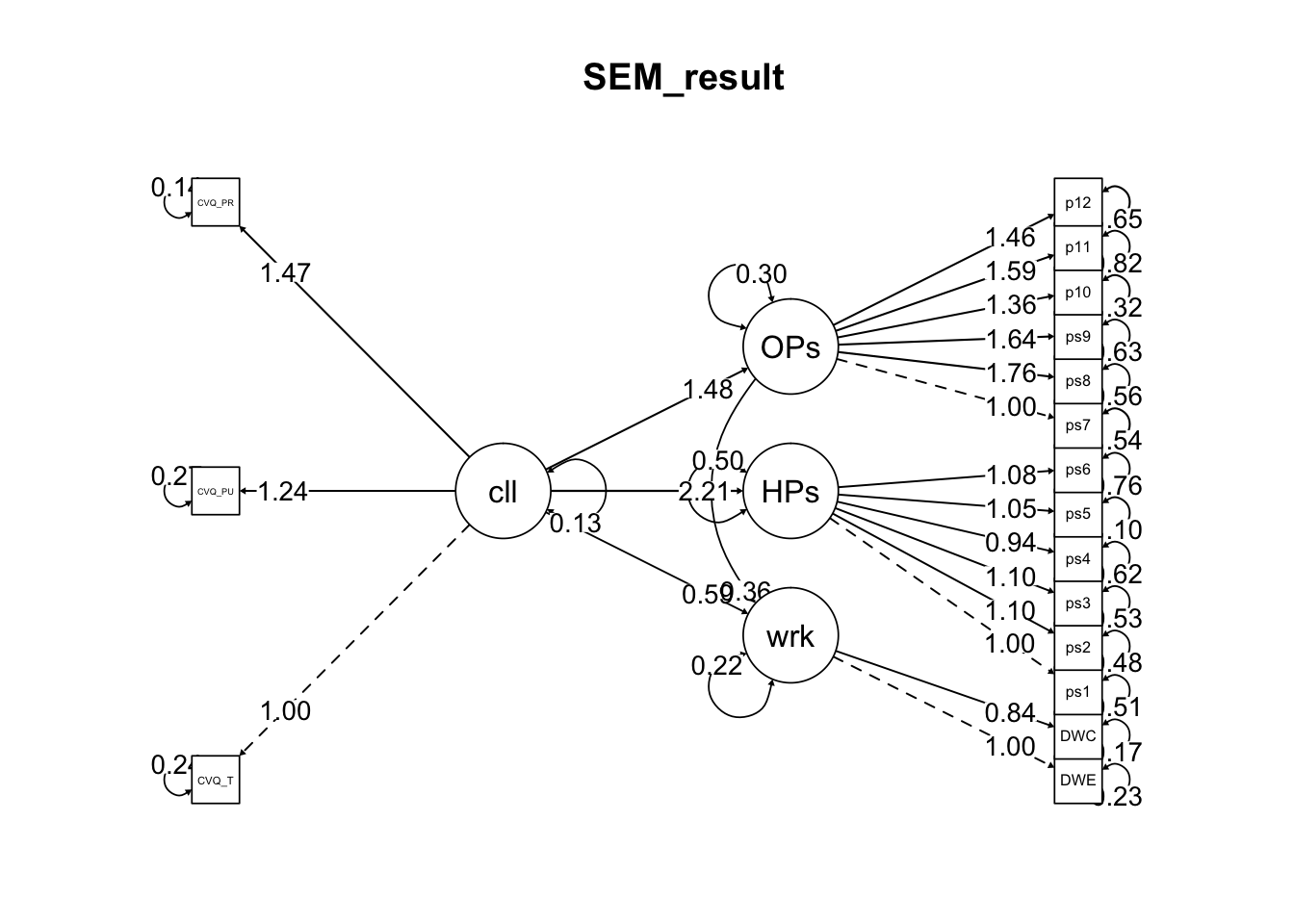
위와 같이 간단하게 그림으로 표현할 수 있습니다.
수업에서 말씀해주셨듯이, 잠재변수가 원 안에 들어가 있어야 하므로, structure.diagram을 활용해서 그려봅니다.
fa(data5, nfactors = 4, fm = "ml", rotate = "promax")$loadings %>% fa.sort %>%
structure.diagram(e.size = .15, digits = 3, cut = .35, main = "EFA Results")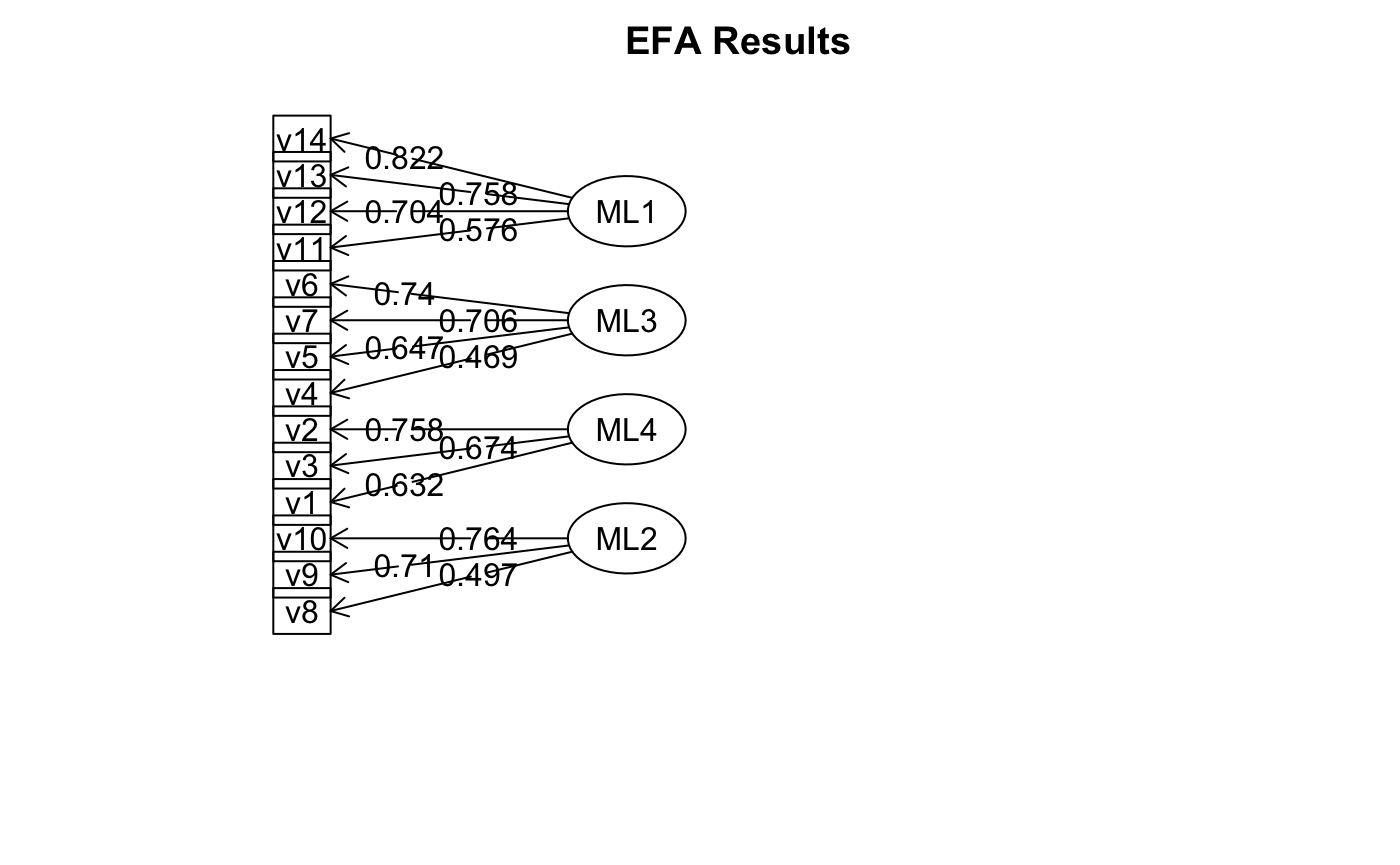
그림1
- 이번에는 semPlot Package를 활용하여 semPaths함수로 그려봅니다.
library(semPlot)## Registered S3 methods overwritten by 'lme4':
## method from
## cooks.distance.influence.merMod car
## influence.merMod car
## dfbeta.influence.merMod car
## dfbetas.influence.merMod carfa(data5, nfactors = 4, fm = "ml", rotate = "promax")$loadings %>%
semPaths(what = "est", edge.label.cex = 1.5, edge.label.position = .8,
edge.color = "black", edge.width = .2, rotation = 4, sizeMan = 4,
shapeMan = "rectangle", sizeLat = 8, title = TRUE, style = "mx",
minimum = .35, cut = .35, width = 600)
title("EFA Result")