Chapter 5 상관분석 - 기본
상관분석/회귀분석은 가장 기본적이면서도 강력한 분석 방법으로
간단한 내용은 엑셀에서도 정말 쉽게 분석 가능합니다.전문 통계 프로그램을 활용하면 시각화 및 고급 분석에 장점이 있으므로,
분석 주제 및 데이터에 맞게 Tool을 선택하시면 될 것 같습니다.지난 시간에 이어, R 내장 데이터인 mtcars 데이터와 아래의 네 가지 패키지를 활용하여 진행하고자 합니다.
* tidyverse : 데이터를 tidy하게 다루기 위한 문법 집대성한 패키지 * tidymodels: 각종 분석을 위한 각종 패키지를 집대성한 패키지 * twidlr : 각종 분석을 tidy하게 진행하는데 도움을 주는 패키지 * corrplot : 상관분석 결과 시각화 패키지이제부터 공유드리는 내용에는 ‘파이프 연산자’ ‘%>%’ 가 활용될 예정이며, 이 연산자를 통해 물이 흘러가듯 데이터가 흘러 들어간다고 생각하시면 됩니다.
아울러, 향후 각종 분석과 머신러닝 등을 위해 tidymodels 패키지를 설치해두시면 조금 더 편하게 분석/머신러닝을 진행하실 수 있습니다.
먼저, 필요한 패키지를 pacman 패키지 p_load 함수를 활용하여 한번에 불러오겠습니다.
- 저는 주로 바로 시각화해서 상관 관계를 확인하기 때문에,
corrplot 패키지로 시각화 하기 을 곧바로 참고해주셔도 됩니다.
5.1 상관분석 시행
cor(데이터): 데이터의 변수 간 상관계수를 구하라
앞서 공유 드렸듯이, mtcars는 총 11개 변수로 구성되어 있습니다.
[, 1] mpg Miles/(US) gallon [, 2] cyl Number of cylinders [, 3] disp Displacement (cu.in.) [, 4] hp Gross horsepower [, 5] drat Rear axle ratio [, 6] wt Weight (1000 lbs) [, 7] qsec 1/4 mile time [, 8] vs Engine (0 = V-shaped, 1 = straight) [, 9] am Transmission (0 = automatic, 1 = manual) [,10] gear Number of forward gears [,11] carb Number of carburetors기본적인 변수간 상관 분석은 cor() 함수를 통해 바로 진행하실 수 있습니다.
## # A tibble: 11 x 12
## .rownames mpg cyl disp hp drat wt qsec vs am
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 mpg 1 -0.852 -0.848 -0.776 0.681 NA 0.419 0.664 0.600
## 2 cyl -0.852 1 0.902 0.832 -0.700 NA -0.591 -0.811 -0.523
## 3 disp -0.848 0.902 1 0.791 -0.710 NA -0.434 -0.710 -0.591
## 4 hp -0.776 0.832 0.791 1 -0.449 NA -0.708 -0.723 -0.243
## 5 drat 0.681 -0.700 -0.710 -0.449 1 NA 0.0912 0.440 0.713
## 6 wt NA NA NA NA NA 1 NA NA NA
## 7 qsec 0.419 -0.591 -0.434 -0.708 0.0912 NA 1 0.745 -0.230
## 8 vs 0.664 -0.811 -0.710 -0.723 0.440 NA 0.745 1 0.168
## 9 am 0.600 -0.523 -0.591 -0.243 0.713 NA -0.230 0.168 1
## 10 gear 0.480 -0.493 -0.556 -0.126 0.700 NA -0.213 0.206 0.794
## 11 carb -0.551 0.527 0.395 0.750 -0.0908 NA -0.656 -0.570 0.0575
## # … with 2 more variables: gear <dbl>, carb <dbl>mtcars 라는 데이터가 cor 라는 상관분석 함수로 들어가서 tidy라는 결과보기 함수로 들어가서 위와 같이 정리되어 보여집니다. 결과를 보면, 상관계수가 꽤 높은 것들도 많이 보입니다.
상관분석 method도 pearson, spearman, kendall 중 선택하실 수 있으며, 이 중 default는 pearson으로 되어 있습니다.
각 방법의 차이와 상관분석의 의미에 대해서는 아래 링크 참고해주시면 됩니다.
5.2 상관분석 통계적 유의성 파악
cor.test(변수1, 변수2, ‘방법’) : 변수1과 변수2의 상관계수를 ’방법’을 활용하여 구하라
cor.mtest(메트릭스 데이터,‘방법’,‘신뢰수준’ ) : ’신뢰수준’에서, ’방법’을 활용하여 매트릭스 데이터 모든 변수의 상관계수를 구하라
두 개의 변수에 대해서만 상관계수 검정을 하실 때는 cor.test 함수를 사용하시면 되고,
두 개 이상의 변수에 대해 상관계수 검정을 하실 때는 cor.mtest 함수를 사용하시면 됩니다.우선, 상관계수가 높게 나온 cyl과 disp의 상관계수 검정을 cor.test 함수를 활용하여 진행해보겠습니다.
# default로 설정되어 있는 pearson 방법을 활용하여 상관계수 검정을 진행해보겠습니다.
cor.test(mtcars$cyl,mtcars$disp, method = 'pearson')##
## Pearson's product-moment correlation
##
## data: mtcars$cyl and mtcars$disp
## t = 11.445, df = 30, p-value = 1.803e-12
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8072442 0.9514607
## sample estimates:
## cor
## 0.9020329검정 결과, p-value가 0.05보다 훨씬 작은 값이 나왔기에
해당 상관 계수는 통계적으로 유의하다고 볼 수 있습니다.“통계적으로 유의하다”는 표현을 앞으로도 자주 사용하게 될텐데, 분석을 하다보니 가장 중요한 것이 통계적인 지식인 것 같습니다. p-value에 대해서는 아래 강의 추천드립니다.
cor.mtest 함수를 사용하면 해당 데이터에 존재하는 모든 변수간 상관계수 검정을 진행할 수 있는데요,
mtcars에 있는 모든 변수에 대해 상관계수 검정을 진행해보겠습니다.cor.mtest 함수를 실행하면, p값이 저장되어 있는 p, 신뢰구간의 하단을 나타내는 lowCI,
신뢰구간의 상단을 나타내는 uppCI 총 3개의 변수로 결과 값이 나옵니다.저는 p값만 사용하며, 변수가 많은 경우, 아래와 같이 출력해서 통계적 유의미성을 확인하는 것은 한계가 있습니다.
## $p
## [,1] [,2] [,3] [,4] [,5]
## [1,] 0.000000e+00 6.112687e-10 9.380327e-10 1.787835e-07 1.776240e-05
## [2,] 6.112687e-10 0.000000e+00 1.802838e-12 3.477861e-09 8.244636e-06
## [3,] 9.380327e-10 1.802838e-12 0.000000e+00 7.142679e-08 5.282022e-06
## [4,] 1.787835e-07 3.477861e-09 7.142679e-08 0.000000e+00 9.988772e-03
## [5,] 1.776240e-05 8.244636e-06 5.282022e-06 9.988772e-03 0.000000e+00
## [6,] 3.478597e-10 4.235741e-08 4.300441e-08 2.120516e-04 1.050519e-05
## [7,] 1.708199e-02 3.660533e-04 1.314404e-02 5.766253e-06 6.195826e-01
## [8,] 3.415937e-05 1.843018e-08 5.235012e-06 2.940896e-06 1.167553e-02
## [9,] 2.850207e-04 2.151207e-03 3.662114e-04 1.798309e-01 4.726790e-06
## [10,] 5.400948e-03 4.173297e-03 9.635921e-04 4.930119e-01 8.360110e-06
## [11,] 1.084446e-03 1.942340e-03 2.526789e-02 7.827810e-07 6.211834e-01
## [,6] [,7] [,8] [,9] [,10]
## [1,] 3.478597e-10 1.708199e-02 3.415937e-05 2.850207e-04 5.400948e-03
## [2,] 4.235741e-08 3.660533e-04 1.843018e-08 2.151207e-03 4.173297e-03
## [3,] 4.300441e-08 1.314404e-02 5.235012e-06 3.662114e-04 9.635921e-04
## [4,] 2.120516e-04 5.766253e-06 2.940896e-06 1.798309e-01 4.930119e-01
## [5,] 1.050519e-05 6.195826e-01 1.167553e-02 4.726790e-06 8.360110e-06
## [6,] 0.000000e+00 2.350024e-01 3.571929e-03 4.184706e-06 2.127455e-03
## [7,] 2.350024e-01 0.000000e+00 1.029669e-06 2.056621e-01 2.425344e-01
## [8,] 3.571929e-03 1.029669e-06 0.000000e+00 3.570439e-01 2.579439e-01
## [9,] 4.184706e-06 2.056621e-01 3.570439e-01 0.000000e+00 5.834043e-08
## [10,] 2.127455e-03 2.425344e-01 2.579439e-01 5.834043e-08 0.000000e+00
## [11,] 4.442021e-02 4.536949e-05 6.670496e-04 7.544526e-01 1.290291e-01
## [,11]
## [1,] 1.084446e-03
## [2,] 1.942340e-03
## [3,] 2.526789e-02
## [4,] 7.827810e-07
## [5,] 6.211834e-01
## [6,] 4.442021e-02
## [7,] 4.536949e-05
## [8,] 6.670496e-04
## [9,] 7.544526e-01
## [10,] 1.290291e-01
## [11,] 0.000000e+00
##
## $lowCI
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1.00000000 -0.9257694 -0.92335937 -0.8852686 0.4360484 -0.94211258
## [2,] -0.92576936 1.0000000 0.80724418 0.6816016 -0.8429083 0.65373588
## [3,] -0.92335937 0.8072442 1.00000000 0.6106794 -0.8487237 0.65335117
## [4,] -0.88526861 0.6816016 0.61067938 1.0000000 -0.6895522 0.35066260
## [5,] 0.43604838 -0.8429083 -0.84872374 -0.6895522 1.0000000 -0.85985889
## [6,] -0.94211258 0.6537359 0.65335117 0.3506626 -0.8598589 1.00000000
## [7,] 0.08195487 -0.7792781 -0.67961513 -0.8475998 -0.2659470 -0.54838490
## [8,] 0.41036301 -0.9039393 -0.84883771 -0.8559675 0.1081948 -0.74667623
## [9,] 0.31755830 -0.7369979 -0.77926901 -0.5456270 0.4843991 -0.87122452
## [10,] 0.15806177 -0.7180260 -0.75751468 -0.4544774 0.4641440 -0.76105702
## [11,] -0.75464796 0.2184331 0.05367539 0.5431200 -0.4259976 0.01099133
## [,7] [,8] [,9] [,10] [,11]
## [1,] 0.08195487 0.4103630 0.3175583 0.15806177 -0.75464796
## [2,] -0.77927809 -0.9039393 -0.7369979 -0.71802597 0.21843307
## [3,] -0.67961513 -0.8488377 -0.7792690 -0.75751468 0.05367539
## [4,] -0.84759984 -0.8559675 -0.5456270 -0.45447743 0.54311998
## [5,] -0.26594700 0.1081948 0.4843991 0.46414402 -0.42599760
## [6,] -0.54838490 -0.7466762 -0.8712245 -0.76105702 0.01099133
## [7,] 1.00000000 0.5346428 -0.5356240 -0.52261830 -0.81780480
## [8,] 0.53464277 1.0000000 -0.1915957 -0.15371324 -0.76613289
## [9,] -0.53562398 -0.1915957 1.0000000 0.61589632 -0.29712041
## [10,] -0.52261830 -0.1537132 0.6158963 1.00000000 -0.08250603
## [11,] -0.81780480 -0.7661329 -0.2971204 -0.08250603 1.00000000
##
## $uppCI
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 1.0000000 -0.7163171 -0.7081376 -0.5860994 0.8322010 -0.7564033
## [2,] -0.7163171 1.0000000 0.9514607 0.9154223 -0.4646481 0.9138772
## [3,] -0.7081376 0.9514607 1.0000000 0.8932775 -0.4805193 0.9137665
## [4,] -0.5860994 0.9154223 0.8932775 1.0000000 -0.1186280 0.8127101
## [5,] 0.8322010 -0.4646481 -0.4805193 -0.1186280 1.0000000 -0.4808135
## [6,] -0.7564033 0.9138772 0.9137665 0.8127101 -0.4808135 1.0000000
## [7,] 0.6696186 -0.3055388 -0.1001493 -0.4774331 0.4263400 0.1515167
## [8,] 0.8223262 -0.6442689 -0.4808327 -0.5006318 0.6839680 -0.1941438
## [9,] 0.7844520 -0.2126675 -0.3055178 0.1152646 0.8501319 -0.5149022
## [10,] 0.7100628 -0.1738615 -0.2565810 0.2332119 0.8427222 -0.2259915
## [11,] -0.2503183 0.7397479 0.6536467 0.8708249 0.2663358 0.6525649
## [,7] [,8] [,9] [,10] [,11]
## [1,] 0.6696186 0.8223262 0.7844520 0.7100628 -0.2503183
## [2,] -0.3055388 -0.6442689 -0.2126675 -0.1738615 0.7397479
## [3,] -0.1001493 -0.4808327 -0.3055178 -0.2565810 0.6536467
## [4,] -0.4774331 -0.5006318 0.1152646 0.2332119 0.8708249
## [5,] 0.4263400 0.6839680 0.8501319 0.8427222 0.2663358
## [6,] 0.1515167 -0.1941438 -0.5149022 -0.2259915 0.6525649
## [7,] 1.0000000 0.8679076 0.1291876 0.1469065 -0.3988165
## [8,] 0.8679076 1.0000000 0.4883712 0.5175379 -0.2756654
## [9,] 0.1291876 0.4883712 1.0000000 0.8949546 0.3982389
## [10,] 0.1469065 0.5175379 0.8949546 1.0000000 0.5684422
## [11,] -0.3988165 -0.2756654 0.3982389 0.5684422 1.00000005.3 상관분석 시각화
저는 앞의 과정들을 생략하고, 주로 corrplot을 그려서 바로 상관관계를 봅니다.
# mtcars 데이터의 모든 변수간 상관계수 검정 진행 후, p.value 로 저장
mtcars%>%cor.mtest(method='pearson')->p.value
#p.value 구조, 변수 확인하기
str(p.value)## List of 3
## $ p : num [1:11, 1:11] 0.00 6.11e-10 9.38e-10 1.79e-07 1.78e-05 ...
## $ lowCI: num [1:11, 1:11] 1 -0.926 -0.923 -0.885 0.436 ...
## $ uppCI: num [1:11, 1:11] 1 -0.716 -0.708 -0.586 0.832 ...먼저 mtcars 변수들에 대해 상관계수 검정을 진행합니다. (pearson 상관계수 양측검정)
str함수를 통해 p.value 의 구조를 살펴보면 p.value는 p값, lowCI값, uppCI 값으로 구성되어 있으며, 저희는 상관계수인 p값만 필요하기에 리스트 첫번째 p.value[[1]] = p값만 뽑아서 사용합니다.
Rstudo에서 할 때는 dev.new() 로 새 창을 열어주고, 아래의 내용을 실행하여 그림을 그려줍니다.
# dev.new() 실습할 때는 # 제거후 확인
mtcars %>% na.omit%>%cor %>% corrplot.mixed(p.mat=p.value[[1]], sig.level=.05, lower = 'number', upper='pie', tl.cex=.6, tl.col='black', order='hclust')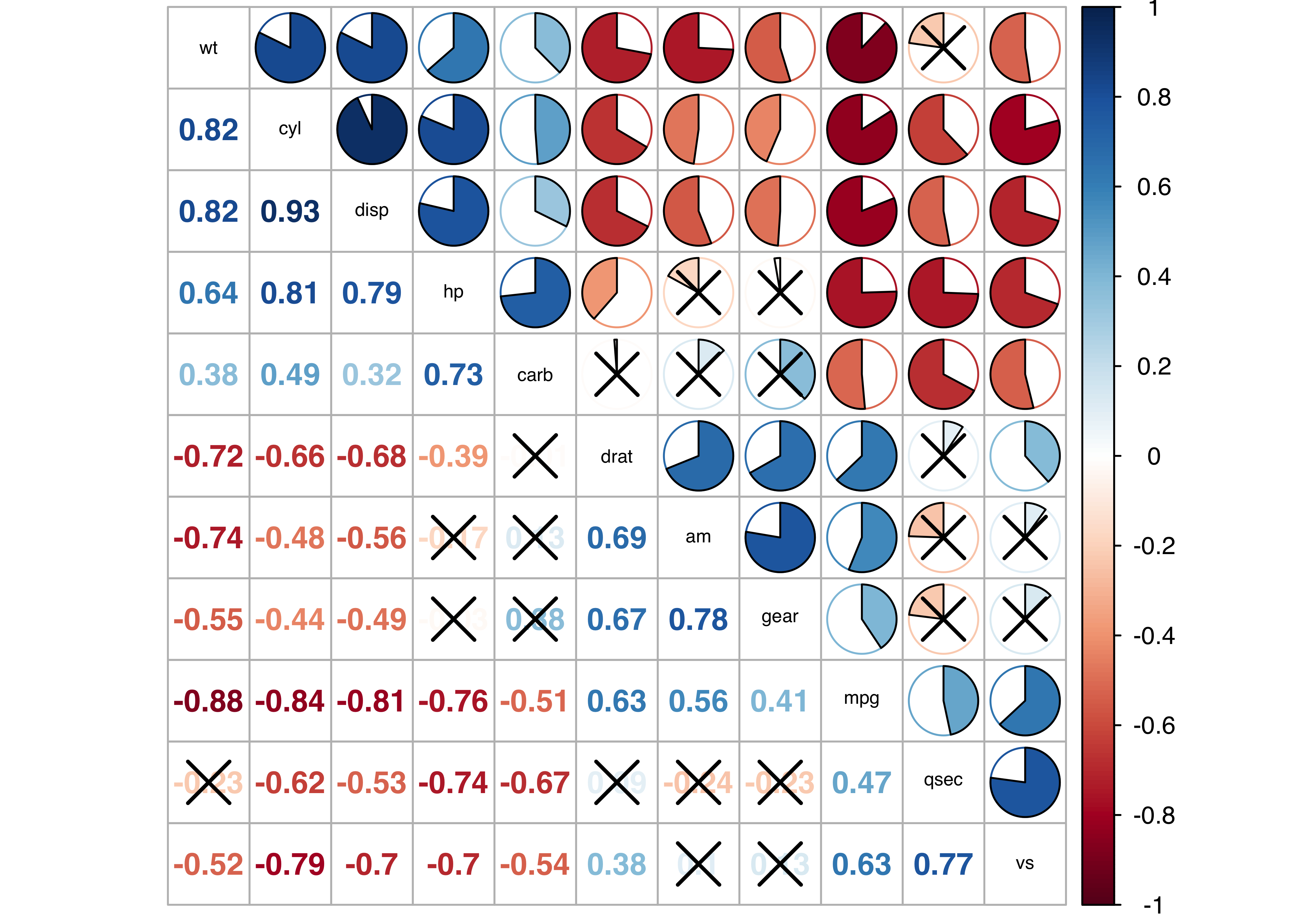
위와 같이 상관분석 결과를 한눈에 보실 수 있으며, 파란색이 진해질수록 정적 상관이, 붉은색이 진해질수록 부적 상관이 크고, pie를 차지하는 면적이 클수록 상관계수가 큼을 알 수 있습니다.
mtcars %>% cor %>% corrplot.mixed(p.mat=p.mat[[1]], sig.level=.05, lower = 'number', upper='pie', tl.cex=.6, tl.col='black',order='hclust')위 코드의 뜻은 다음과 같습니다. mtcars 원 데이터를 cor 함수에 넣어서 상관 분석을 한 뒤, corrplot.mixed 함수에 넣어 시각화를 진행합니다.
corrplot.mixed 함수 내부의 옵션은 정말 여러가지가 있는데, 제가 주로 사용하는 것은 다음과 같습니다.
* p.mat : 상관계수 검정결과 * sig.level : 유의확율이며, sig.level 보다 큰 경우, 그림에 x표시됨 * upper/lower : 윗부분/아랫부분을 어떤 타입을 나타낼지 선택해줌 * order = hclust : 계층적 군집 결과에 따라 변수의 순서를 배열해줌 * tl.col ='black' : 중간 대각선 텍스트 라벨의 색을 검정색으로 지정함 * tl.cex = .6 : 중간 대각선 텍스트 라벨의 크기를 0.6으로 정함이 외에도 corrplot에는 다양한 기능들이 있는데, 더 자세한 내용은 아래 링크 참조 부탁드립니다.