Chapter 8 세 집단 이상 비교 ANOVA
- ANOVA 시작에 앞서 자료 유형에 따른 통계분석 방법에 대해 아래와 같이 공유 드립니다. (ctrl키+마우스휠로 크기 조정 가능합니다.)
전부 다 활용하지는 않지만, 분석하시고자 하는 방향과 자료 유형에 따라 다양한 통계분석 방법을 R을 통해 쉽게 해보실 수 있습니다.
얕은 지식을 기반으로 기존 자료들을 짜깁기하여 만들어 보았는데, 잘못된 부분을 발견하신다면 말씀 부탁 드립니다.
오늘은 앞서 활용했던 IBM의 HR데이터를 활용하여 One-way ANOVA 를 시행해보겠습니다.
One-way ANOVA는 독립변인 1개, 종속변인 1개 인경우 활용하는 분석 방법입니다.
이번에는 세 집단 이상에서 학력 (전문대졸 미만, 전문대졸, 대졸, 석사, 박사) 수준에 따라’직무만족’에 유의미한 차이를 보이는지 확인하고자 합니다.
두 집단의 유의미한 차이를 분석하는 t Test를 6번 하면 되는 것 아니냐고 하실 수도 있지만, t Test를 6번 하게 되면, 1종 오류(아닌데 맞다고 하는 경우)를 범할 확률이 매우 높다고 합니다.
통계는 분산의 마법이라는 이야기가 있던데, 저는 여러번 들어서 겨우 이해했지만, 아래 강의 추천드립니다.
- 우선 필요한 라이브러리를 불러옵니다.
8.1 데이터 불러오기/전처리
데이터 불러오기/전처리는 지난 시간에 진행한 내용 참고하시어 동일하게 진행해주시면 됩니다.
지난 시간에 RDS 데이터로 저장해두었으므로, 불러오겠습니다.
8.2 ANOVA 준비
8.2.1 독립변인 종속변인 데이터 불러오기
- 독립변인은 지난 번 t Test와 동일하게 ‘학력’으로 두고, 종속변인은 ’직무만족’ 으로 두겠습니다.
- IBM.HR 데이터 중, Education과 JobSatisfaction 변수만 골라서 IBM.HR.test 데이터로 저장했고, 데이터를 확인해보겠습니다.
## Rows: 1,470
## Columns: 2
## $ Education <int> 2, 1, 2, 4, 1, 2, 3, 1, 3, 3, 3, 2, 1, 2, 3, 4, 2, 2…
## $ JobSatisfaction <int> 4, 2, 3, 3, 2, 4, 1, 3, 3, 3, 2, 3, 3, 4, 3, 1, 2, 4…8.2.2 학력’별 ‘직무만족’ boxplot으로 확인하기
#그래프를 보여주는 새 창을 띄우고(실제 실행시 # 지우고 실행하세요)
#dev.new()
#Jobsatisfaction을 종속(y), Education을 독립(X)로 하는 boxplot을 그리고, 색(col)은 5가지 무지개색으로 지정합니다.
boxplot(JobSatisfaction ~ Education,IBM.HR.test, col=rainbow(5))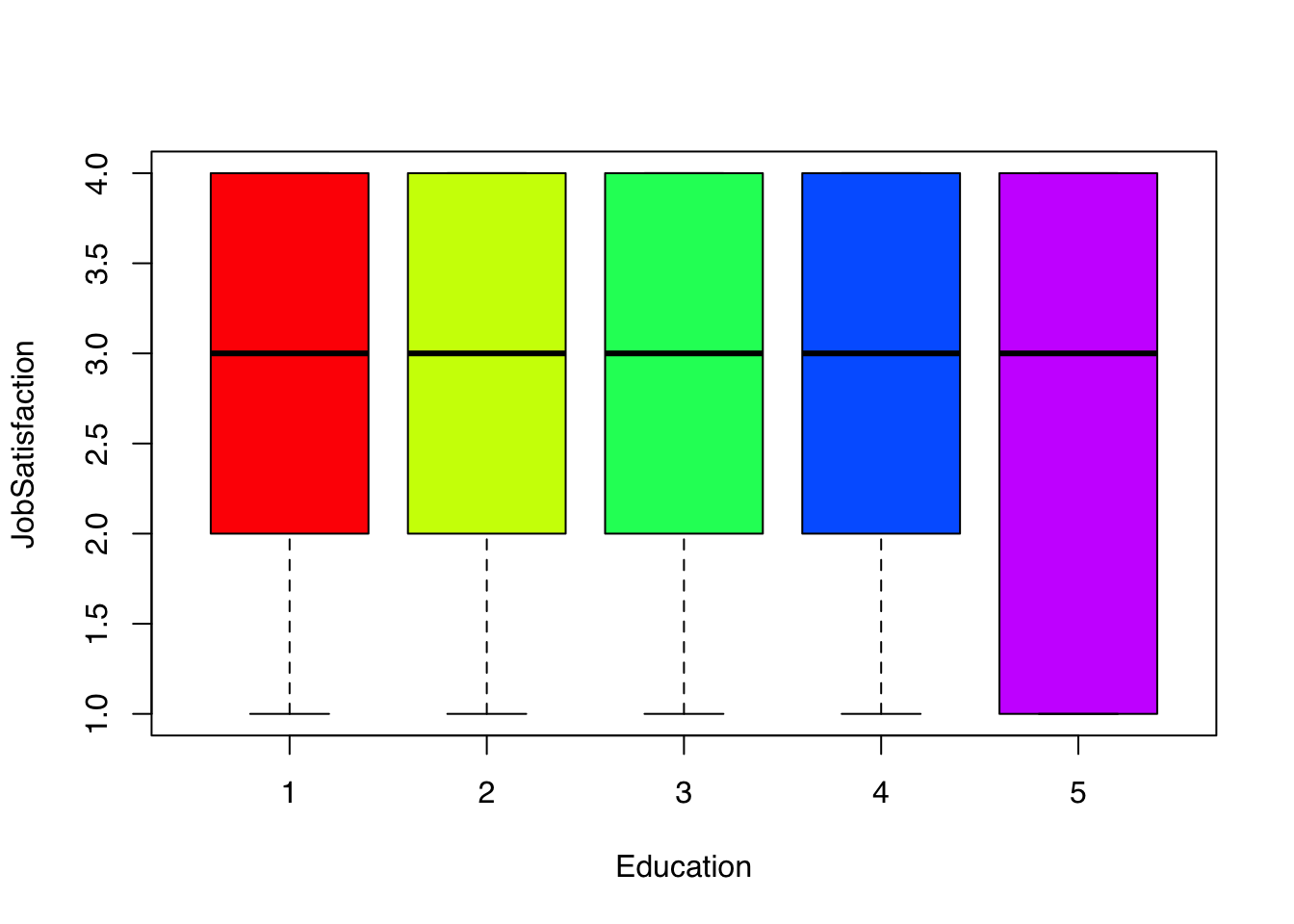
설문 데이터의 경우, 5점 척도이기에 집단간 차이가 있는지 boxplot으로 판단하기는 쉽지 않습니다.
boxplot 결과를 보면 대졸미만 ~ 석사 까지는 비슷한데, 박사만 직무만족의 IQR이 다른 것 같습니다.
8.2.3 one-way ANOVA를 위해 독립변수를 factor 형태로 변환
as.factor(데이터/변수) : 데이터/변수를 factor type으로 변환하라
- 분산분석을 하실 때는, 독립변수를 factor형으로 변환해주셔야 합니다.
데이터 타입/class에 대해서는 추후 더 자세히 다루도록 하겠습니다.
## Rows: 1,470
## Columns: 2
## $ Education <fct> 2, 1, 2, 4, 1, 2, 3, 1, 3, 3, 3, 2, 1, 2, 3, 4, 2, 2…
## $ JobSatisfaction <int> 4, 2, 3, 3, 2, 4, 1, 3, 3, 3, 2, 3, 3, 4, 3, 1, 2, 4…## Rows: 1,470
## Columns: 2
## $ Education <fct> 2, 1, 2, 4, 1, 2, 3, 1, 3, 3, 3, 2, 1, 2, 3, 4, 2, 2…
## $ JobSatisfaction <int> 4, 2, 3, 3, 2, 4, 1, 3, 3, 3, 2, 3, 3, 4, 3, 1, 2, 4…- IBM.HR.test의 Education변수를 factor 형으로 바꾼 후, fct 로 바뀌었음을 확인 하실 수 있습니다.
8.3 ANOVA 실행
aov(종속 ~ 독립, 데이터): 데이터에 있는 독립변수와 종속변수로 ANOVA 분석을 진행하라
R에서 one-way ANOVA 분석은 aov 함수를 통해 진행하실 수 있습니다.
코드는 아래와 같이 구성하시면 됩니다.
aov(독립변수~종속변수(그룹변수), data=데이터명)
학력에 따라 직무만족에 유의미한 차이가 있는지 ANOVA 해보겠습니다.
## Call:
## stats::aov(formula = formula, data = data)
##
## Terms:
## Education Residuals
## Sum of Squares 6.2014 1780.4986
## Deg. of Freedom 4 1465
##
## Residual standard error: 1.102432
## Estimated effects may be unbalanced8.4 ANOVA 결과 확인
위 결과 값을 보시면, ANOVA 분석 결과를 확인할 수 있는 F 값이 나타나지 않습니다.
일반적으로는 summary 함수를 통해 확인하지만, 저희는 tidymodels 패키지를 활용하기에 tidy 함수를 활용하여 결과를 볼 수 있습니다.
## # A tibble: 2 x 6
## term df sumsq meansq statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Education 4 6.20 1.55 1.28 0.277
## 2 Residuals 1465 1780. 1.22 NA NA위 결과에서 statistic이 F value를 의미하며, 통계적으로 유의한지는 p-value를 보시면 됩니다.
p-value는 0.277로 0.05보다 커서 ’학력’에 따른 ’직무만족’의 차이는 유의미하지 않은 것으로 보시면 됩니다.
8.5 등분산성 확인
bartlett.test(종속 ~ 독립, 데이터): 데이터에 있는 종속, 독립 변인으로 K개의 표본이 등분산성을 갖는지 검정하라
분산분석의 경우, 집단간 등분산성을 만족해야 합니다.
one-way ANOVA에서 만약 통계적으로 유의미한 차이가 있다고 나오는 경우, 반드시 등분산성을 만족하는지 테스트를 해주셔야 합니다.
##
## Bartlett test of homogeneity of variances
##
## data: JobSatisfaction by Education
## Bartlett's K-squared = 0.65405, df = 4, p-value = 0.9569위에서 p-value가 0.05 보다 크므로, Education 5개 집단의 분산이 다르다는 대립가설을 기각하므로, 등분산성을 만족한다고 보시면 됩니다.
bartlett.test 외, levene.test() 함수도 많이 사용하십니다.
8.6 사후검정 시행
3개 집단 이상의 차이가 있는지 aov() 함수로 분석하신 뒤에는 반드시 사후검정을 해주셔야 어떤 집단간에 차이가 있었는지 확인하실 수 있습니다.
aov()는 그저, 집단간에 차이가 있다/없다 정도만을 알려줄 뿐, 어느 집단 간 차이가 있는지 알려주지 않습니다.
사후 검정에는 본페로니(Bonferroni), 튜키 (Tukey), 쉐페 (Scheffe)의 방법 등이 일반적으로 사용되며, 자세한 내용은 아래의 링크 참조 부탁 드립니다.
8.6.1 Tukey 사후검정 시행
TukeyHSD(aov한 결과) : aov한 결과에서, 어떤 집단끼리 차이가 있는지 보여달라
- 여러 방법 중, 저는 주로 Tukey 방법을 활용합니다. 아래와 같이 아주 간단하게 Tukey 사후검정을 하실 수 있습니다.
## # A tibble: 10 x 6
## term comparison estimate conf.low conf.high adj.p.value
## <chr> <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Education 2-1 -0.0305 -0.323 0.262 0.999
## 2 Education 3-1 -0.148 -0.411 0.115 0.539
## 3 Education 4-1 -0.0136 -0.289 0.262 1.00
## 4 Education 5-1 -0.133 -0.625 0.359 0.947
## 5 Education 3-2 -0.117 -0.336 0.102 0.586
## 6 Education 4-2 0.0169 -0.217 0.251 1.00
## 7 Education 5-2 -0.103 -0.573 0.367 0.975
## 8 Education 4-3 0.134 -0.0622 0.331 0.336
## 9 Education 5-3 0.0146 -0.438 0.467 1.00
## 10 Education 5-4 -0.120 -0.580 0.340 0.954term은 보고자 했던 학력(Education)이고, 집단간 비교를 Comparison으로 표시했습니다.
첫번째 행을 보면, Education 값이 2인 전문대졸 집단과, Education 값이 1인 전문대졸 이하 집단을 비교한 것입니다. p-value가 0.05보다 매우 크므로, 집단간 차이가 없음을 알 수 있습니다.
앞서 one-way ANOVA 결과에서 학력 수준에 따라 직무만족에 차이가 없음을 확인했으니, 집단간 차이를 보아도 전부 차이가 없게 나올 수 밖에 없습니다.
위와 같은 과정을 통해 3개 이상의 집단간 통계적으로 유의미한 차이가 있는지 확인하실 수 있습니다.