第 5 章 数值模拟
空间广义线性混合效应模型在广义线性混合效应模型基础上添加了与空间位置相关的随机效应,这种随机效应在文献中常称为空间效应 (Diggle, Tawn, and Moyeed 1998)。 它与采样点的位置、数量都有关系, 其中采样点的位置决定空间过程的协方差结构, 而采样点的数量决定空间效应的维度,从而导致空间广义线性混合效应模型比普通的广义线性混合效应模型复杂。作为过渡,我们在第 5.1.1 和 5.1.2 节模拟了一维和二维平稳高斯过程。 第 5.2 节模拟 SGLMM 模型, 分两个小节展开叙述,第 5.2.1 小节模拟响应变量服从二项分布的情形, 第 5.2.2 小节模拟响应变量服从泊松分布的情形,在这两个小节里,比较了第4章第4.4.3小节介绍的贝叶斯马尔科夫链蒙特卡罗算法(简称贝叶斯 MCMC)和第4.5节介绍的贝叶斯 Stan-HMC 算法的表现,贝叶斯 MCMC 算法基于 R 包 geoRglm 内置的 Langevin-Hastings 算法实现,贝叶斯 Stan-HMC 算法基于 Stan 内置的 HMC 算法实现。
5.1 平稳空间高斯过程
5.1.1 一维平稳空间高斯过程
一维情形下,平稳高斯过程 \(S(x)\) 的自协方差函数采用幂指数型,见公式 (5.2)。特别地,当 \(\kappa = 1\) 时,自协方差函数为指数型,见公式 (5.1)。下面分 \(\kappa =1\) 和 \(\kappa =2\),模拟两个一维的平稳空间高斯过程,设置共同的协方差参数为 \(\sigma^2 = 1\),\(\phi = 0.15\),均值向量为 \(\mathbf{0}\)。
首先在区间\([-2,2]\)上,产生 2000 个服从均匀分布的随机数,根据这些随机数的位置,分别以自协方差函数公式 (5.1) 和 (5.2) 计算得到 2000 维的服从高斯分布的协方差矩阵 \(G\),为保证协方差矩阵的正定性,在矩阵对角线上添加扰动 \(1 \times 10^{-12}\),然后根据 Cholesky 分解该对称正定矩阵,即可得到下三角块 \(L\),使得 \(G = L \times L^{\top}\),再产生 2000 个服从标准正态分布的随机向量 \(\eta\),而 \(L\eta\) 即为所需的服从平稳高斯过程的一组随机数。
图5.1模拟了一维平稳空间高斯过程,自协方差函数分别为指数型 (5.1) 和幂二次指数型 (5.2),均值为 \(\mathbf{0}\),协方差参数 \(\sigma^2 = 1\),\(\phi = 0.15\),横坐标表示采样的位置,纵坐标是目标值 \(S(x)\),图中 2000 个灰色点表示服从相应随机过程的随机数,橘黄色点是从中随机选择的 36 个点。 \[\begin{align} \mathsf{Cov}(S(x_i), S(x_j)) & = \sigma^2 \exp\big\{ - \frac{|x_{i} - x_{j}|}{ \phi } \big\} \tag{5.1} \\ \mathsf{Cov}(S(x_i), S(x_j)) & = \sigma^2 \exp\big\{ -\big( \frac{ |x_{i} - x_{j}| }{ \phi } \big) ^ {\kappa} \big\}, 0 < \kappa \leq 2 \tag{5.2} \end{align}\]
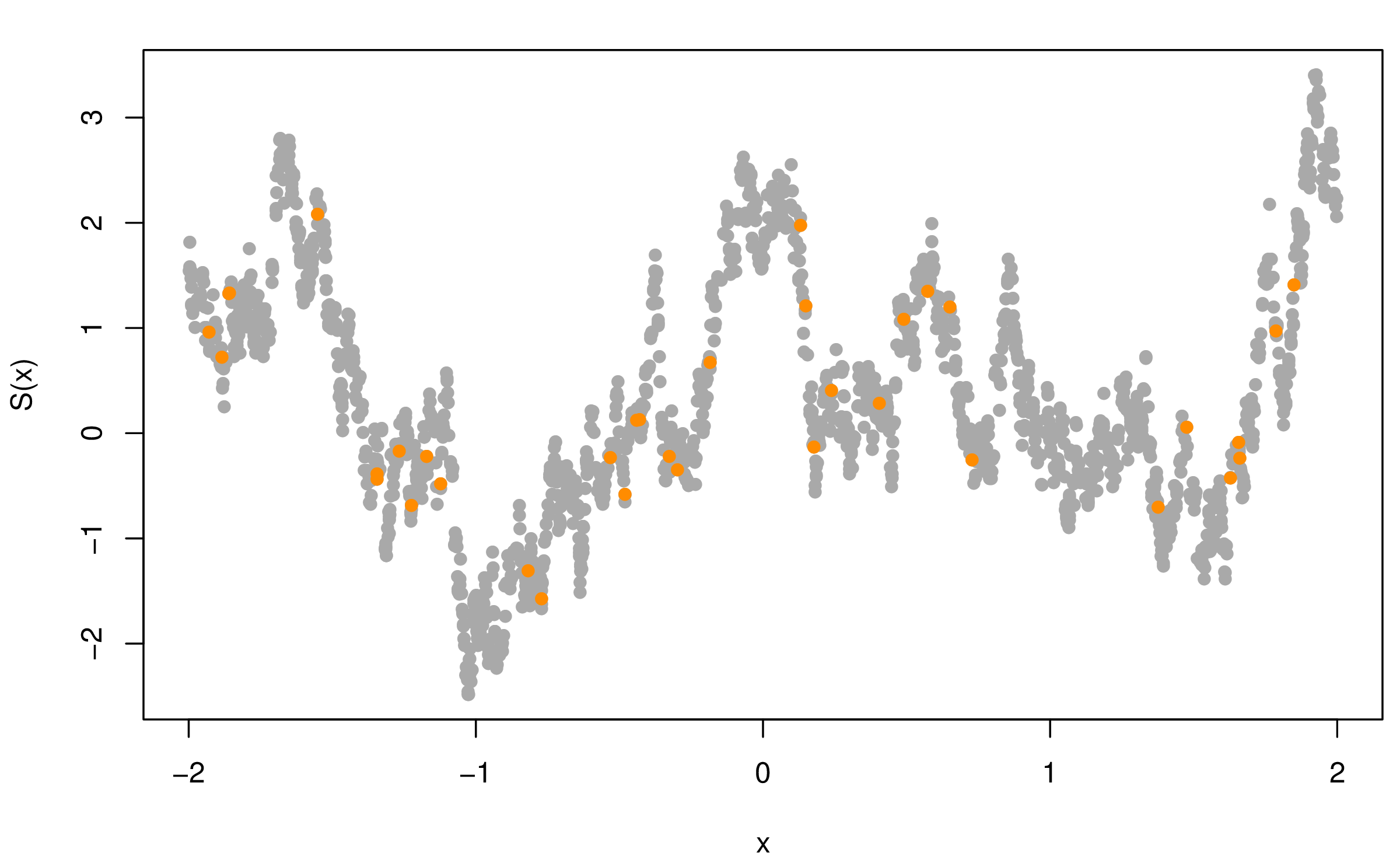
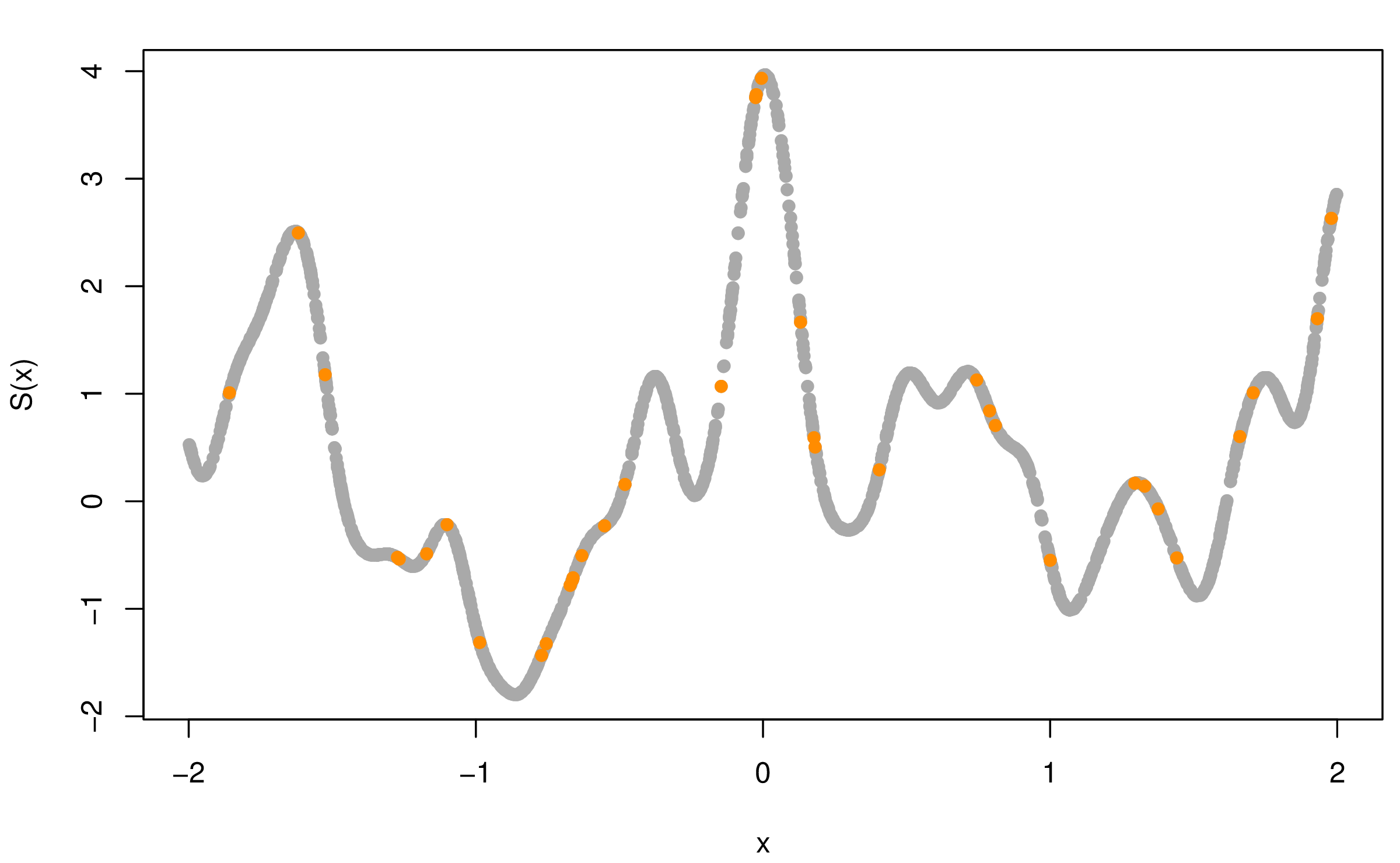
图 5.1: 模拟一维平稳空间高斯过程
根据定理 2.4,指数型协方差函数的平稳高斯过程在原点连续但是不可微,而幂二次指数型协方差函数在原点无穷可微,可微性越好图像上表现越光滑。对比图 5.1 的两个子图, 可以看出,在协方差参数 \(\sigma^2 = 1\),\(\phi = 0.15\) 相同的情况下,\(\kappa\) 越大越光滑。
5.1.2 二维平稳空间高斯过程
二维情形下,在规则平面上模拟平稳高斯过程 \(\mathcal{S} = S(x), x \in \mathbb{R}^2\), 其均值向量为零向量 \(\mathbf{0}\), 协方差函数为指数型,见公式 (5.1),协方差参数 \(\phi = 1, \sigma^2 = 1\)。在单位平面区域为 \([0,1] \times [0,1]\) 模拟服从上述二维平稳空间高斯过程,不妨将此区域划分为 \(6 \times 6\) 的小网格,而每个格点作为采样的位置,共计 36 个采样点,在这些采样点上的观察值即为目标值 \(S(x)\)。
类似本章第 5.1.1 节模拟一维平稳空间过程的步骤, 首先根据采样点位置坐标和协方差函数 (5.1) 计算得目标空间过程的 \(\mathcal{S}\) 协方差矩阵 \(G\),然后使用 R 包 MASS 提供的 mvrnorm 函数产生多元正态分布随机数,与 5.1.1 节不同的是这里采用特征值分解,即 \(G = L\Lambda L^{\top}\),与 Cholesky 分解相比,特征值分解更稳定些,但是 Cholesky 分解更快,Stan 即采用此法,后续过程与一维模拟一致。模拟获得的随机数用图 5.2 表示, 格点上的值即为平稳空间高斯过程在该点的取值,为方便显示,已四舍五入保留两位小数,图中的橘黄色点是采样的位置,自协方差函数为指数型。
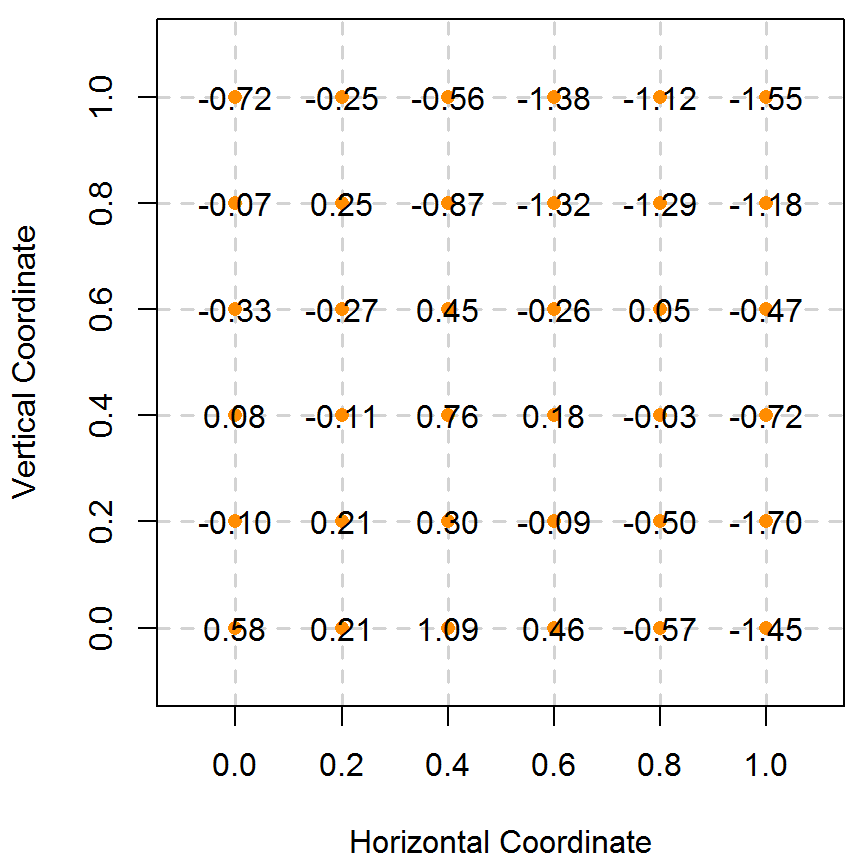
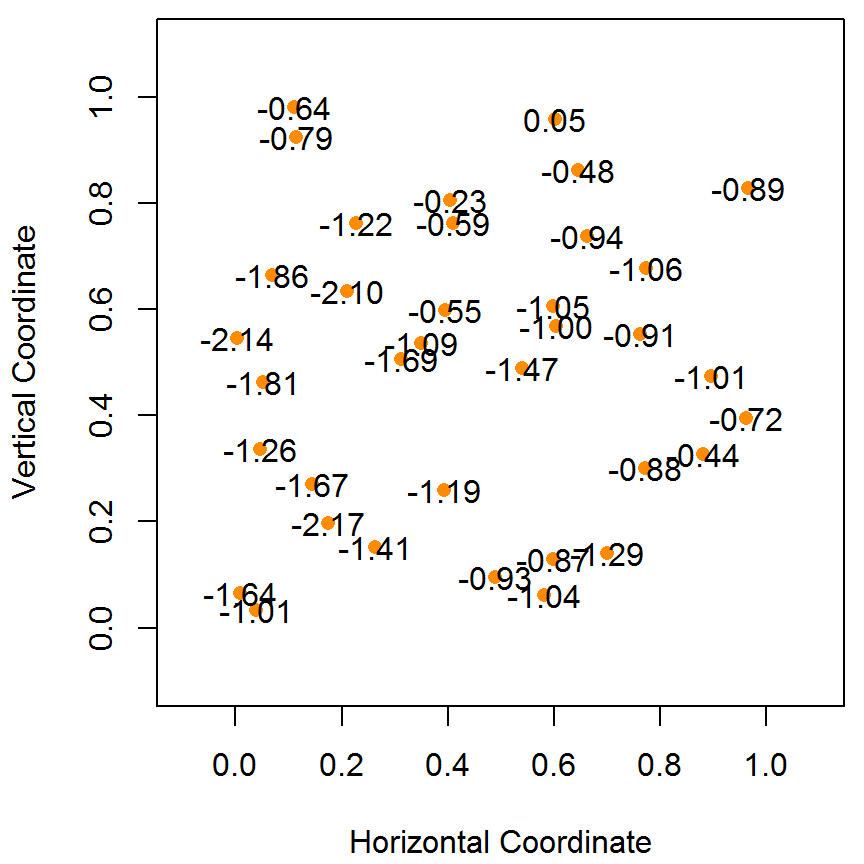
图 5.2: 模拟二维平稳空间高斯过程
同 5.1.1 节,二维平稳空间高斯过程 \(S(x)\) 的协方差函数也可以为更一般的梅隆型,如公式 (5.3) 所示。 \[\begin{equation} \rho(u) = \sigma^2 \{ 2^{\kappa -1} \Gamma(\kappa) \}^{-1}( u/\phi )^{\kappa} \mathcal{K}_{\kappa}( u / \phi ) \tag{5.3} \end{equation}\] 且在区域 \([0,1] \times [0,1]\) 上也可以随机采点,如图 5.2 的右子图所示。
模拟平稳空间高斯过程的实现方法: Ribeiro 和 Diggle 开发了 geoR 包 (Ribeiro Jr. and Diggle 2001),提供的 grf 函数除了实现 Cholesky 分解,还实现了奇异值分解,特征值分解等算法分解协方差矩阵\(G\)。当采样点不太多时,Cholesky 分解已经足够好,下面的第 5.2 节对平稳空间高斯过程的数值模拟即采用此法,当采样点很多,为了加快模拟的速度,可以选用 Schlather 等开发的 RandomFields 包 (Schlather et al. 2015),内置的 GaussRF 函数实现了用高斯马尔科夫随机场近似平稳空间高斯过程的算法,此外,Rue 等 (2009年) (Rue, Martino, and Chopin 2009) 也实现了从平稳高斯过程到高斯马尔科夫随机场的近似算法,开发了比较高效的 INLA 程序库 (Lindgren and Rue 2015),其内置的近似程序得到了一定的应用 (Marta Blangiardo, n.d.; Xiaofeng Wang and Faraway, n.d.)。
5.2 空间广义线性混合效应模型
5.2.1 响应变量服从二项分布
响应变量服从二项分布 \(Y_{i} \sim \mathrm{Binomial}(m_{i},p(x_{i}))\),即在位置 \(x_i\) 处以概率 \(p(x_i)\) 重复抽取了 \(m_i\) 个样本,总样本数 \(M=\sum_{i=1}^{N}m_i\),\(N\) 是采样点的个数,模拟二项型空间广义线性混合效应模型为 (5.4),联系函数为 \(g(\mu_i) = \log\{\frac{p(x_i)}{1-p(x_i)}\}\),\(S(x)\) 是均值为 \(\mathbf{0}\),协方差函数为 \(\mathsf{Cov}(S(x_i),S(x_j)) = \sigma^2 \big\{2^{\kappa-1}\Gamma(\kappa)\big\}^{-1}(u/\phi)^{\kappa}K_{\kappa}(u/\phi), \kappa = 0.5\) 的平稳空间高斯过程。
\[\begin{equation}
g(\mu_i) = \log\big\{\frac{p(x_i)}{1-p(x_i)}\big\} = \alpha + S(x_i) \tag{5.4}
\end{equation}\]
设置固定效应参数 \(\alpha = 0\),协方差参数为 \(\boldsymbol{\theta} = (\sigma^2, \phi) = (0.5, 0.2)\),采样点数目为 \(N = 64\),每个采样点抽取的样本数 \(m_i = 4, i = 1, 2, \ldots, 64\),则 \(Y_i\) 的取值范围为 \(0, 1, 2, 3, 4\)。首先模拟平稳空间高斯过程 \(S(x)\),在单位区域 \([0,1] \times [0,1]\) 划分为 \(8 \times 8\) 的网格,格点选为采样位置,用 geoR 包提供的 grf 函数产生协方差参数为 \(\boldsymbol{\theta} = (\sigma^2,\phi) = (0.5, 0.2)\) 的平稳空间高斯过程,由公式 (5.4) 可知 \(p(x_i) = \exp[\alpha + S(x_i)]/\{1 + \exp[\alpha + S(x_i)]\}\), 即每个格点处二项分布的概率值,然后依此概率,由 rbinom 函数产生服从二项分布的观察值 \(Y_i\),模拟的数据集可以用图 5.3 直观表示,格点是采样点的位置,左图表示二维规则平面上的平稳空间高斯过程,其上的数字是 \(p(x)\) 的值,为方便显示,已经四舍五入保留两位小数,右图表示观察值 \(Y\) 随空间位置的变化,格点上的值即为观察值 \(Y\),图中的两个圈分别标记第1个(左下)和第29个(右上)采样点。
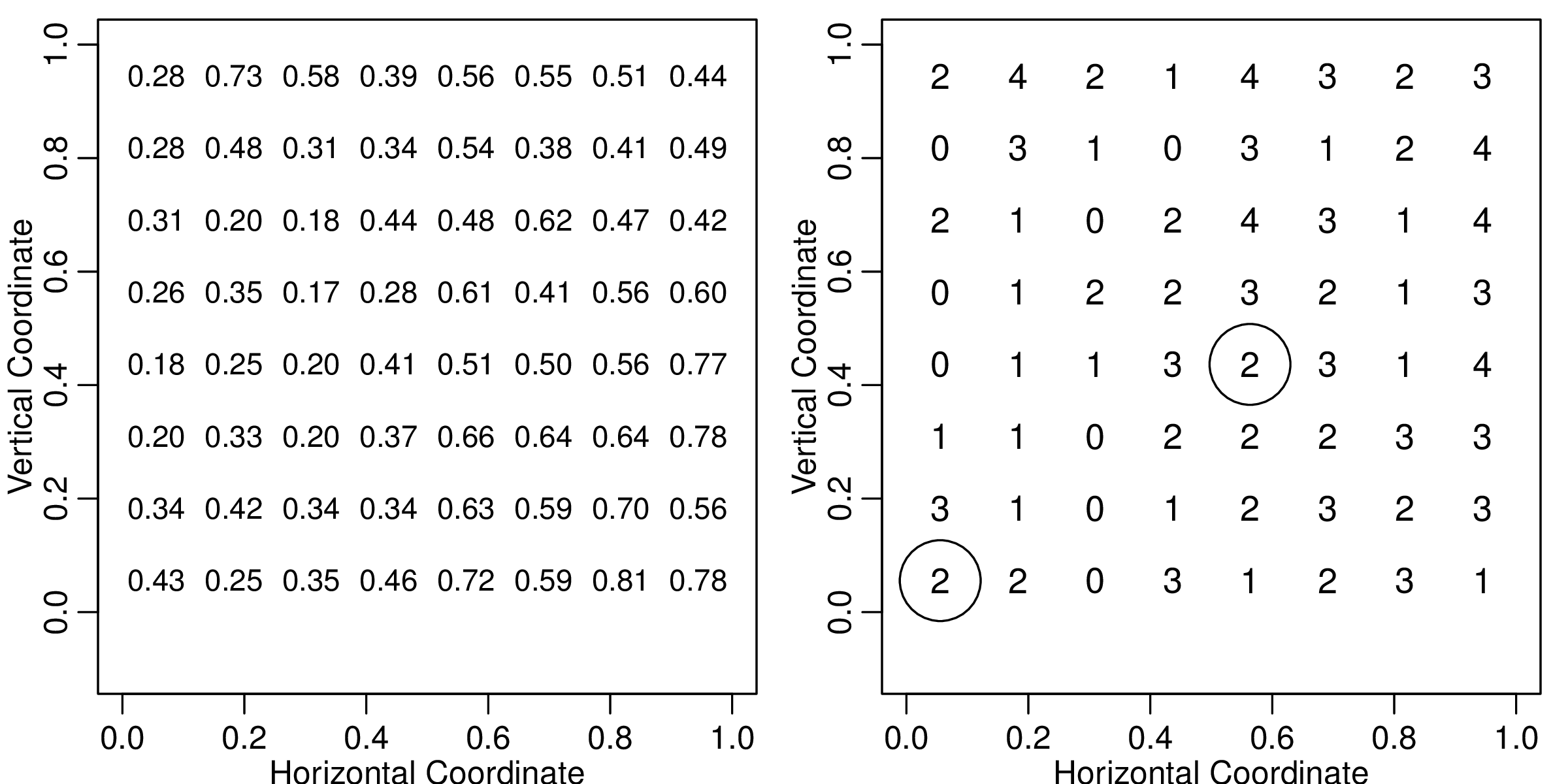
图 5.3: 模拟二项型空间广义线性混合效应模型
基于 Langevin-Hastings 采样器实现的马尔科夫链蒙特卡罗算法,参数 \(\alpha\) 的先验分布选均值为 0,方差为 1 的标准正态分布,参数 \(\phi\) 的先验分布选期望为 0.2 的指数分布,参数 \(\sigma^2\) 的先验分布是非中心的逆卡方分布(scaled inverse Chi square distribution),其非中心化参数为 0.5,自由度为 5,各参数的先验选择参考 Christensen 和 Ribeiro (2002年) (Christensen and Ribeiro Jr. 2002)。Langevin-Hastings 算法运行 110000 次迭代,前 10000 次迭代用作预处理,后 10 万次迭代里间隔 100 次迭代采样,获得关于参数 \(\alpha,\phi,\sigma^2\) 的后验分布的样本,样本量是 1000。 \[\begin{equation} \alpha \sim \mathcal{N}(0,1), \quad \phi \sim \mathrm{Exp}(0.2), \quad \sigma^2 \sim \mathrm{Inv-}\chi^2(5,0.5) \end{equation}\] 参数 \(\alpha,\phi,\sigma^2\) 的贝叶斯估计没有显式表达式,通常以 MCMC 算法获得后验分布的样本均值作为参数的估计。贝叶斯估计的定义是使得估计的均方误差达到最小时的估计,因此贝叶斯估计的精度或者说好坏常用后验分布的方差衡量,因为均方误差在参数估计取后验均值时是后验方差,故而表 5.1 不再提供估计的均方误差值,而是提供了 5 个后验分布的分位点,在 95% 的置信水平下,样本分位点 0.025 和 0.975 的值组成了置信区间的上下界。以采样点个数 \(N =64\)为例,除了获得各参数的估计值外,还获得 64 个采样点处 \(p(x_i), i = 1, \ldots, 64\) 的后验均值、方差、标准差和 5个分位点,详见附表 7.1。
Langevin-Hastings 算法与 HMC 算法的数值模拟比较见表5.1,前者在 R 软件里基于 geoRglm 包实现,后者基于 Stan 实现。表格中的列依次是模型参数 \(\alpha,\phi,\sigma^2\) 的真值(初值)、后验均值、后验方差、后验的 5个分位点、样本量\(N\)和算法运行时间(单位:秒)。采样点数目分别考虑了 \(N = 36, 64, 81\) 的情况,对于每组参数设置,重复模拟了 100 次,表格前半部分是 Langevin-Hastings 算法得到的结果,后半部分是 HMC 算法得到的结果。
| true(init) | mean | var | 2.5% | 25% | 50% | 75% | 97.5% | N | time(s) | |
|---|---|---|---|---|---|---|---|---|---|---|
| LH | ||||||||||
| \(\alpha\) | 0.0(0.387) | -0.354 | 0.079 | -0.938 | -0.524 | -0.361 | -0.173 | 0.215 | 36 | 600.12 |
| \(\phi\) | 0.2(0.205) | 0.121 | 0.006 | 0.005 | 0.055 | 0.110 | 0.180 | 0.285 | ||
| \(\sigma^2\) | 0.5(1.121) | 0.683 | 0.147 | 0.215 | 0.408 | 0.596 | 0.850 | 1.667 | ||
| \(\alpha\) | 0.0(0.157) | 0.003 | 0.089 | -0.596 | -0.169 | 0.013 | 0.179 | 0.609 | 64 | 729.19 |
| \(\phi\) | 0.2(0.110) | 0.194 | 0.004 | 0.070 | 0.145 | 0.195 | 0.250 | 0.295 | ||
| \(\sigma^2\) | 0.5(0.494) | 0.656 | 0.096 | 0.254 | 0.449 | 0.592 | 0.781 | 1.453 | ||
| \(\beta\) | 0.0(-0.006) | -0.155 | 0.044 | -0.565 | -0.284 | -0.156 | -0.03 | 0.273 | 81 | 844.56 |
| \(\phi\) | 0.2(0.185) | 0.116 | 0.006 | 0.005 | 0.055 | 0.105 | 0.17 | 0.280 | ||
| \(\sigma^2\) | 0.5(0.403) | 0.468 | 0.057 | 0.180 | 0.311 | 0.414 | 0.56 | 1.129 | ||
| HMC | ||||||||||
| \(\alpha\) | 0.0(-0.813) | -0.230 | 0.209 | -1.127 | -0.521 | -0.214 | 0.056 | 0.653 | 36 | 6.65 |
| \(\phi\) | 0.2(1.692) | 1.103 | 0.364 | 0.459 | 0.721 | 0.936 | 1.284 | 2.669 | ||
| \(\sigma^2\) | 0.5(0.144) | 0.474 | 0.187 | 0.105 | 0.216 | 0.333 | 0.573 | 1.572 | ||
| \(\alpha\) | 0.0(0.155) | 0.046 | 0.251 | -0.947 | -0.269 | 0.049 | 0.356 | 1.069 | 64 | 27.70 |
| \(\phi\) | 0.2(1.766) | 1.042 | 0.246 | 0.471 | 0.708 | 0.921 | 1.247 | 2.324 | ||
| \(\sigma^2\) | 0.5(0.808) | 0.647 | 0.228 | 0.170 | 0.338 | 0.524 | 0.779 | 1.958 | ||
| \(\alpha\) | 0.0(-0.369) | -0.082 | 0.170 | -0.893 | -0.321 | -0.078 | 0.174 | 0.742 | 81 | 45.69 |
| \(\phi\) | 0.2(0.911) | 1.110 | 0.331 | 0.453 | 0.721 | 0.986 | 1.330 | 2.506 | ||
| \(\sigma^2\) | 0.5(0.302) | 0.410 | 0.105 | 0.105 | 0.205 | 0.317 | 0.503 | 1.211 |
为了获得尽量好的效果,在样本量 \(N = 64\) 时,花了大量时间反复试错调了 Langevin-Hastings 算法的参数,相比较而言,得到了一组还不错的结果。然而,当改变样本量时,又需要漫长的调参,因此样本量是36和81时,只要求迭代序列保持收敛即可。基于 Stan 实现的 HMC 算法没有调参数,初值是随机生成的,先验分布是默认的,总迭代次数设为2000次,前1000次迭代作为预处理,后1000次的迭代值全部采样,所有的迭代序列都通过了平稳性检验。
根据模拟的过程和表5.1的结果来看,基于 Stan 实现的 HMC 算法更易收敛,且对初始值和先验分布不那么敏感,不需要耗时的调参过程。表 5.1 中 Langevin-Hastings 算法的时间由 R 内置的函数 system.time() 记录。初始值是 burn-in 的位置,即完成预处理开始采样的第一个迭代点。
5.2.2 响应变量服从泊松分布
模拟响应变量 \(Y\) 服从泊松分布,即 \(Y_i \sim \mathrm{Poisson}(\lambda(x_{i}))\) 的泊松型空间广义线性混合效应模型 \[\begin{equation} g(\mu_i) = \log[\lambda(x_i)] = \alpha + S(x_i) \tag{5.5} \end{equation}\] 其中,\(S(x)\) 是平稳空间高斯过程,其均值为 \(\mathbf{0}\),协方差函数为 \(\mathrm{Cov}(S(x_i),S(x_j)) = \sigma^2 \big\{2^{\kappa-1}\Gamma(\kappa)\big\}^{-1}(u/\phi)^{\kappa}K_{\kappa}(u/\phi)\),联系函数 \(g(\mu_i) = \log[\lambda(x_{i})]\)。
类似 5.2.1 小节,首先产生服从平稳空间高斯过程 \(S(x)\) 的随机数 \(S(x_i),i=1,\ldots,N\),然后由 (5.5) 式可得 \(\lambda(x_i) = \exp(\alpha + S(x_i))\),且响应变量 \(Y_i \sim \mathrm{Poisson}(\lambda(x_{i}))\),根据 R 内置函数 rpois 即可 产生服从参数为 \(\lambda(x_i)\) 的泊松分布的随机数。Langevin-Hastings 算法和 HMC 算法模拟的结果见表 5.2。HMC 算法包含有效样本数 \(n_{eff}\)、 潜在尺度缩减因子 \(\hat{R}\) 和蒙特卡罗均值误差 se_mean 的完整表格见附表 7.2,参数迭代序列的收敛性分析已在第2 章第4.5.3节给出,这里不再赘述,所有的模拟实验都是在完成收敛性分析后给出的。
在模型(5.5)的设置下,Langevin-Hastings 算法和 HMC 算法的比较见表5.2,模型参数真值为 \(\alpha = 0.5, \phi = 0.2, \sigma^2 = 2.0, \kappa = 1.5\),采样点数目分别为 \(N=36,64,100\),对于每组参数设置,重复模拟了 100 次。表格各列依次是参数的真值(初始值)、后验均值、后验方差、后验五个分位点、样本量和算法运行时间(单位:秒)。表格前半部分是 Langevin-Hastings 算法实现的结果,后半部分是 Stan 实现的结果。
| true(init) | mean | var | 2.5% | 25% | 50% | 75% | 97.5% | N | time(s) | |
|---|---|---|---|---|---|---|---|---|---|---|
| LH | ||||||||||
| \(\alpha\) | 0.5(1.201) | 0.527 | 0.418 | -0.759 | 0.189 | 0.514 | 0.855 | 1.864 | 36 | 642.66 |
| \(\phi\) | 0.2(0.420) | 0.401 | 0.052 | 0.100 | 0.240 | 0.360 | 0.520 | 0.960 | ||
| \(\sigma^2\) | 2.0(1.038) | 1.311 | 0.660 | 0.365 | 0.766 | 1.081 | 1.584 | 3.562 | ||
| \(\alpha\) | 0.5(1.211) | 0.866 | 1.517 | -1.610 | 0.059 | 0.870 | 1.666 | 3.159 | 64 | 883.76 |
| \(\phi\) | 0.2(0.480) | 0.682 | 0.073 | 0.300 | 0.480 | 0.640 | 0.820 | 1.380 | ||
| \(\sigma^2\) | 2.0(2.232) | 3.932 | 2.594 | 1.667 | 2.800 | 3.642 | 4.744 | 7.740 | ||
| \(\alpha\) | 0.5(0.189) | 0.323 | 0.657 | -1.449 | -0.124 | 0.416 | 0.812 | 1.831 | 100 | 1223.28 |
| \(\phi\) | 0.2(0.540) | 0.617 | 0.085 | 0.220 | 0.400 | 0.560 | 0.785 | 1.320 | ||
| \(\sigma^2\) | 2.0(1.395) | 1.479 | 0.498 | 0.545 | 0.941 | 1.352 | 1.822 | 3.195 | ||
| HMC | ||||||||||
| \(\alpha\) | 0.5(0.335) | 0.483 | 0.310 | -0.608 | 0.094 | 0.488 | 0.851 | 1.613 | 36 | 11.25 |
| \(\phi\) | 0.2(0.066) | 0.631 | 0.036 | 0.362 | 0.501 | 0.602 | 0.722 | 1.090 | ||
| \(\sigma^2\) | 2.0(0.347) | 1.370 | 0.298 | 0.455 | 0.977 | 1.317 | 1.714 | 2.566 | ||
| \(\alpha\) | 0.5(1.021) | 0.498 | 0.402 | -0.775 | 0.082 | 0.534 | 0.917 | 1.798 | 64 | 113.04 |
| \(\phi\) | 0.2(0.370) | 0.385 | 0.003 | 0.285 | 0.343 | 0.380 | 0.422 | 0.509 | ||
| \(\sigma^2\) | 2.0(2.610) | 2.473 | 0.292 | 1.585 | 2.102 | 2.416 | 2.804 | 3.734 | ||
| \(\alpha\) | 0.5(0.613) | 0.400 | 0.297 | -0.723 | 0.062 | 0.415 | 0.767 | 1.412 | 100 | 272.58 |
| \(\phi\) | 0.2(0.294) | 0.299 | 0.005 | 0.181 | 0.243 | 0.289 | 0.343 | 0.465 | ||
| \(\sigma^2\) | 2.0(1.724) | 1.146 | 0.206 | 0.525 | 0.824 | 1.037 | 1.395 | 2.282 |
100 个采样点的模拟实验中,不断试错调了 Langevin-Hastings 算法的参数,得到比较好的估计值,在该组参数设置下,更改采样点数目分别为 36 和 64,又需要重新调整 Langevin-Hastings 算法的参数设置,以获得参数的后验分布和后验量的估计值。
在同组参数设置下,基于 Stan 实现的 HMC 算法与 Langevin-Hastings 算法相比,效果要好,其一体现在后验方差更小,也是贝叶斯估计下的均方误差更小,见表 5.2;其二对于应用的意义更大,它不需要调参数,对先验分布的要求更加宽松;其三算法收敛的更快,基于 Langevin-Hastings 算法实现的贝叶斯 MCMC 算法迭代次数设置为 110000,前 10000 次迭代作为预处理,间隔 100 次迭代采样,收集到的样本量是 1000。而基于 Stan 实现的 HMC 算法只进行了 2000 次迭代,前 1000 次迭代作为预处理阶段,后 1000 次迭代全部采样,所以样本量也是 1000。
这里要补充说明一下,比较两个算法却在迭代次数上做了不同的设置,是因为首先要保证模型参数的迭代序列收敛,只有这样才能作参数的后验估计,那么同样达到收敛状态,Langevin-Hastings 算法大约 110000 次迭代,而基于 Stan 实现的 HMC 算法大约 2000 次迭代,如果强行继续增加 HMC 算法的迭代次数是意义不大的,因为它已经收敛,增加迭代次数只会无端添加算法运行时间。
5.3 本章小结
geoRglm 包实现的 Langevin-Hastings 算法,相比较而言,收敛速度慢,迭代序列自相关性表现拖尾,因此在上述模拟实验中,为了降低相关性,采样间隔取 100,这就直接要求增加总的迭代次数以达到足够的后验样本量,这样才能用于后验量的计算。此外,在调参数的过程中面临不收敛的情况是常有的,而这个不收敛的原因至少有两个,其一是参数初值不合适,其二是总迭代次数不够。因此,我们也遭遇了 Christensen 迭代上百万次的情形,在尽量保持统一的参数设置下,我们选择继续调整参数,而保持总迭代次数 110000 次不变。在每组模型设置下都获得最佳的参数,这无疑是一件十分耗时的工作,因为该算法的参数只有不断试错才能获得更加合适的参数设置,在已经收敛的情形下调参数,这个过程会更加漫长。
基于 Stan 实现的贝叶斯 Stan-HMC 算法,其内置的 HMC 算法是结合了 NUTS 采样器(Hoffman and Gelman 2014),搜索模型参数的策略更加友好,不需要手动调参数,只需要指定合适的参数先验,使得迭代序列保持收敛即可,编程过程中,模型参数的重参数化(reparameterization)对迭代进程和结果会产生一定影响,如第2章第4.5.3小节基于 Eight Schools 数据集介绍分层正态模型就对参数 \(\mu\) 和 \(\sigma\) 做了重参数化。
基于似然推断的算法,如第4章第4.4.2小节介绍的蒙特卡罗极大似然算法和第4.4.1小节介绍的拉普拉斯近似算法,都需要非常接近真值的参数初值,才能得到好的结果,因为在大多数情形下,SGLMM 模型的对数似然曲面是呈现山岭或峡谷状,局部极值点多而且对数似然函数值变化不大,导致收敛速度极慢或者陷入局部极值点的收敛,非常难获得全局极值点。因此,一个合适的策略是在合理的初值周围打网格,格点作为迭代初值,以不同的初值进行迭代,将计算的剖面似然函数轮廓画在二维平面上,通过这种降维观察的方式,获得一个可靠的全局极值点,作为参数的最佳似然估计,在后续的第6章第6.2节以分析朗格拉普岛核污染数据集为例介绍这一策略。
参考文献
Christensen, O. F., and P. J. Ribeiro Jr. 2002. “geoRglm: A Package for Generalised Linear Spatial Models.” R News 2 (2): 26–28.
Diggle, Peter J., J. A. Tawn, and R. A. Moyeed. 1998. “Model-Based Geostatistics.” Journal of the Royal Statistical Society, Series C 47 (3): 299–350.
Hoffman, Matthew D., and Andrew Gelman. 2014. “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.” Journal of Machine Learning Research 15 (1): 1593–1623.
Lindgren, Finn, and Håvard Rue. 2015. “Bayesian Spatial Modelling with R-INLA.” Journal of Statistical Software 63 (19): 1–25.
Marta Blangiardo, Michela Cameletti. n.d. Spatial and Spatio-Temporal Bayesian Models with R-INLA. Chichester, UK: John Wiley; Sons Inc.
Ribeiro Jr., Paulo J., and Peter J. Diggle. 2001. “geoR: A Package for Geostatistical Analysis.” R News 1 (2): 14–18.
Rue, Håvard, Sara Martino, and Nicholas Chopin. 2009. “Approximate Bayesian Inference for Latent Gaussian Models Using Integrated Nested Laplace Approximations (with Discussion).” Journal of the Royal Statistical Society, Series B 71 (2): 319–92.
Schlather, Martin, Alexander Malinowski, Peter J. Menck, Marco Oesting, and Kirstin Strokorb. 2015. “Analysis, Simulation and Prediction of Multivariate Random Fields with Package RandomFields.” Journal of Statistical Software 63 (8): 1–25.
Xiaofeng Wang, Ryan Yue, and Julian Faraway. n.d. Bayesian Regression with INLA. Boca Raton, Florida: Chapman; Hall/CRC.