第 4 章 参数估计
模型的参数估计是建模分析的重要步骤,鉴于空间广义线性混合效应模型(简称 SGLMM)的复杂性,文献中的参数估计方法,如最小二乘估计(简称 LSE)和极大似然估计(简称 MLE) 都没有显式的表达式,因此必须发展有效的算法。
目前,文献中的出现的算法有拉普拉斯近似极大似然算法、蒙特卡罗极大似然算法、贝叶斯Langevin-Hastings 算法和低秩近似算法。第4.1节,第4.2节和第4.3节分别介绍 SGLMM 模型的极大似然估计,空间线性混合模型下的剖面似然估计和用于近似高维积分的拉普拉斯近似方法。似然函数卷入空间随机效应带来的高维积分,为此,文献中出现了三类估计模型参数的算法,分别是第 4.4.1 小节介绍的拉普拉斯近似极大似然算法(简称LAML)、第 4.4.2 小节介绍的蒙特卡罗极大似然算法(简称 MCML), 第 4.4.3 小节介绍的贝叶斯框架下的Langevin-Hastings算法 (简称贝叶斯 LH),第 4.4.4 小节介绍的低秩近似算法(简称 Low-Rank)。
第 4.5 节详细介绍在贝叶斯 Langevin-Hastings 算法的基础上提出基于 Stan 实现的汉密尔顿蒙特卡罗算法(简称 Stan-HMC 算法),并分四个小节进行,第4.5.2小节介绍算法提出的背景和意义,第 4.5.3 小节从 Stan 的发展、内置算法设置以及与同类软件的比较等三方面介绍,然后以数据集 Eight Schools 为例子介绍 Stan 的使用,为空间广义线性混合效应模型的 Stan 实现作铺垫,第4.5.4小节介绍 Stan-HMC 算法实现过程。
4.1 极大似然估计
设研究区域 \(D \subseteq \mathbb{R}^2\), 对于第 \(i\) 次观测, \(s_i\) 表示区域 \(D\) 内的位置,\(y(s_i)\) 表示响应变量,\(\mathbf{x}(s_i), i = 1, \ldots, n\) 是一个 \(p\) 维的固定效应,定义如下的 SGLMM 模型: \[ \mathrm{E}[y(s_i)|u(s_i)] = g^{-1}[\mathbf{x}(s_i)^{\top}\boldsymbol{\beta} + \mathbf{u}(s_i)], \quad i = 1, \ldots, n \]
其中, \(g(\cdot)\) 是实值可微的逆联系函数, \(\boldsymbol{\beta}\) 是 \(p\) 维的回归参数向量,代表 SGLMM 模型的固定效应。随机过程 \(\{U(\mathbf{s}): \mathbf{s} \in D\}\) 是平稳的空间高斯过程,其均值为 \(\mathbf{0}\), 自协方差函数 \(\mathsf{Cov}(U(\mathbf{s}),U(\mathbf{s}')) = C(\mathbf{s} - \mathbf{s}'; \boldsymbol{\theta})\), \(\boldsymbol{\theta}\) 表示其中的参数向量。 \(\mathbf{u} = (u(s_1),u(s_2),\ldots,u(s_n))^{\top}\) 是平稳空间高斯过程 \(U(\cdot)\) 的一个实例。给定 \(\mathbf{u}\)的情况下,观察值 \(\mathbf{y} = (y(s_1),y(s_2),\ldots,y(s_n))^{\top}\) 是相互独立的。
给定 \(u_i = u(s_i), i = 1, \ldots, n\)的条件下, \(y_i = y(s_i)\) 的条件概率密度函数是 \[ f(y_i|u_i;\boldsymbol{\beta}) = \exp[a(\mu_i)y_i - b(\mu_i)]c(y_i) \]
其中, \(\mu_i = \mathsf{E}(y_i|u_i)\), \(a(\cdot),b(\cdot)\) 和 \(c(\cdot)\) 是特定的函数,具体的情况视所服从的分布而定,第2章第2.1节就不同的分布给出了不同函数形式。 SGLMM 模型的边际似然函数
\[\begin{equation} L(\boldsymbol{\psi};\mathbf{y}) = \int \prod_{i=1}^{n} f(y_i|u_i;\boldsymbol{\beta})\phi_{n}(\mathbf{u};0,\Sigma_{\boldsymbol{\theta}})\mathrm{d}\mathbf{u} \tag{4.1} \end{equation}\]
记号 \(\boldsymbol{\psi} = (\boldsymbol{\beta},\boldsymbol{\theta})\) 表示 SGLMM 模型的全部参数, \(\phi_{n}(\cdot;0,\Sigma_{\boldsymbol{\theta}})\) 表示 \(n\) 元正态密度函数,其均值为 \(\mathbf{0}\), 协方差矩阵为 \(\Sigma_{\boldsymbol{\theta}} = (c_{ij}) = (C(s_i - s_j; \boldsymbol{\theta})), i,j = 1, \ldots, n\)。 边际似然函数 (4.1) 几乎总是卷入一个难以处理的积分,这是主要面临的问题,并且计算量随观测 \(y_i\) 的数量增加,此积分的维数等于观测点的个数。
再从贝叶斯方法的角度来看 SGLMM 模型, 令 \(\mathbf{y} = (y(s_1),\ldots,y(s_n))^{\top}\) 表示观测值, \(\pi(\boldsymbol{\psi})\) 表示模型参数的联合先验密度,那么联合后验密度为
\[\begin{equation} \begin{aligned} \pi(\boldsymbol{\psi},\mathbf{u}|\mathbf{y}) &= \frac{f(\mathbf{y|\mathbf{u}, \boldsymbol{\psi}})\phi_{n}(\mathbf{u};0,\Sigma_{\boldsymbol{\theta}})\pi(\boldsymbol{\psi})}{m(\mathbf{y})} \\ m(\mathbf{y}) &= \int f(\mathbf{y|\mathbf{u}, \boldsymbol{\psi}})\phi_{n}(\mathbf{u};0,\Sigma_{\boldsymbol{\theta}})\pi(\boldsymbol{\psi})\mathrm{d} \mathbf{u} \mathrm{d} \boldsymbol{\psi} \end{aligned} \end{equation}\]
同样遭遇难以处理的高维积分问题,所以 \(m(\mathbf{y})\) 亦不会有显式表达式。特别地,若取 \(\pi(\boldsymbol{\psi})\) 为扁平先验 (flat priors) ,如 \(\pi(\boldsymbol{\psi}) \propto 1\), 后验分布将简化为似然函数 (4.1) 的常数倍。 如果导出的后验是合适的, MCMC 算法可以用来研究似然函数, 但是对很多 SGLMM 模型扁平先验会导出不合适的后验 (improper posteriors) (Natarajan and McCulloch 1995), 所以选用模糊先验 (diffuse prior)来导出合适的后验 (proper posteriors),导出的后验能接近似然函数,并不要求后验模 (posterior mode) 完全是似然函数的极大似然估计 MLE (Kass and Wasserman 1996)。
4.2 剖面似然估计
极大似然估计是一种被广泛接受的参数估计方法,因其优良的大样本性质,在宽松的正则条件下,极大似然估计服从渐近正态分布,满足无偏性,而且是有效的估计。为了叙述方便,似然函数能有显式表达式,考虑空间线性混合效应模型,即响应变量服从正态分布的情况,以此来介绍剖面似然估计 (profile likelihood estimate)(Peter J. Diggle and Ribeiro Jr., n.d.)。 \[\begin{equation} \mathbf{Y} \sim \mathcal{N}(D\boldsymbol{\beta},\sigma^2 \mathbf{R}(\phi) + \tau^2\mathbf{I}) \tag{4.2} \end{equation}\] 其中, \(D\) 是 \(n \times p\) 的观测数据矩阵,\(\boldsymbol{\beta}\) 是\(p\times 1\)维的回归参数向量,\(\mathbf{R}\) 依赖于 \(\phi\),这里\(\phi\) 可能含有多个参数。模型 (4.2) 的对数似然函数 \[\begin{equation} \begin{aligned} L(\boldsymbol{\beta},\tau^2,\sigma^2,\phi) = {} & - 0.5\{ n\log(2\pi) + \log\{|(\sigma^2\mathbf{R}(\phi)+\tau^2\mathbf{I})|\} \\ & + (\mathbf{Y} - D\boldsymbol{\beta})^{\top}(\sigma^2\mathbf{R}(\phi)+\tau^2\mathbf{I})^{-1}(\mathbf{Y} - D\boldsymbol{\beta}) \} \end{aligned} \tag{4.3} \end{equation}\] 极大化 (4.3) 式就是求模型 (4.2) 参数的极大似然估计,极大化对数似然的过程分步如下:
- 重参数化 \(\nu^2 = \tau^2/\sigma^2\),令 \(V = \mathbf{R}(\phi) + \nu^2 \mathbf{I}\);
- 给定 \(V\),对数似然函数 (4.3) 在 \[\begin{equation} \begin{aligned} \hat{\boldsymbol{\beta}}(V) & = (D^{\top} V^{-1} D)^{-1} D^{\top} V^{-1}\mathbf{Y} \\ \hat{\sigma}^2(V) & = n^{-1} \{\mathbf{Y} - D\hat{\boldsymbol{\beta}}(V)\}^{\top} V^{-1} \{\mathbf{Y} - D\hat{\boldsymbol{\beta}}(V)\} \end{aligned} \tag{4.4} \end{equation}\] 取得极大值;
- 将 (4.4) 式代入对数似然函数 (4.3) 式,可获得一个简化的对数似然 \[\begin{equation} L_{0}(\nu^2,\phi) = - 0.5\{ n\log(2\pi) + n\log \hat{\sigma}^2(V) + \log |V| + n \} \tag{4.5} \end{equation}\]
- 关于参数 \(\nu^2, \phi\) 极大化 (4.5) 式,获得参数 \(\nu^2, \phi\) 的估计值,再将其回代 (4.4) 式,获得估计值 \(\hat{\boldsymbol{\beta}}\) 和 \(\hat{\sigma}^2\)。
在空间线性混合效应模型的设置下,上述极大化似然函数的过程可能与自协方差函数的类型有关,如在使用 Matérn 型自协方差函数的时,平滑参数 \(\kappa\) 也卷入到 \(\phi\) 中,导致识别问题。因此,让 \(\kappa\) 分别取 \(0.5,1.5,2.5\),使得平稳空间高斯过程 \(\mathcal{S}\) 覆盖到不同程度的均方可微性 (Warnes and Ripley 1987)。原则上,极大似然估计的变化情况可以通过观察对数似然函数的曲面来分析2,但是,似然曲面的维数往往不允许直接观察。在这种情形下,另一个基于似然的想法是剖面似然 (profile likelihood)。一般地,假定有一个模型含有参数 \((\alpha,\phi)\),其参数的似然函数表示为 \(L(\alpha,\phi)\)。则关于 \(\alpha\) 的剖面似然函数定义为 \[\begin{equation} L_{p}(\alpha) = L(\alpha,\hat{\psi}(\alpha)) = \max_{\psi} (L(\alpha,\psi)) \tag{4.6} \end{equation}\] 即考虑似然函数随 \(\alpha\) 的变化情况,对每一个 \(\alpha\) (保持 \(\alpha\) 不变),指定 \(\psi\) 的值使得对数似然取得最大值。剖面似然就是让我们可以观察到关于 \(\alpha\) 的似然曲面,显然,其维数比完全似然曲面要低,与只有一个参数的对数似然一样,它也可以用来计算单个参数的置信区间。现在,注意到简化的对数似然 (4.5) 其实可以看作模型 (4.2) 关于 \((\nu^2,\phi)\) 的剖面对数似然 (Peter J. Diggle and Ribeiro Jr., n.d.)。
4.3 拉普拉斯近似
先回顾一下基本的泰勒展开,将一个函数 \(f(x)\) 在点 \(a\) 处展开成和的形式,有时候是无穷多项,可以使用其中的有限项作为近似,通常会选用前三项,即到达函数 \(f(x)\) 二阶导的位置。 \[ f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \ldots \] 以基本的抛物线函数 \(f(x) = x^2\) 为例,考虑将它在 \(a = 2\) 处展开。首先计算 \(f(x)\) 的各阶导数 \[\begin{align*} &{} f(x) = x^2, \quad f'(x) = 2x, \\ &{} f''(x) = 2 \quad f^{(n)}(x) = 0, \quad n = 3,4,\ldots \end{align*}\] 因此,\(f(x)\) 可以展开成有限项的和的形式 \[ f(x) = x^2 = 2^2 + 2(2)(x-2) + \frac{2}{2}(x-2)^2 \] 拉普拉斯近似本质上是用正态分布来近似任意分布 \(g(x)\),用泰勒展开的前三项近似 \(\log g(x)\),展开的位置是密度函数 \(g(x)\) 的极值点 \(\hat{x}\),则有 \[ \log g(x) \approx \log g(\hat{x}) + \frac{\partial \log g(\hat{x})}{\partial x} (x - \hat{x}) + \frac{\partial^2 \log g(\hat{x})}{2\partial x^2} (x - \hat{x})^2 \] 由于是在函数 \(g(x)\) 的极值点 \(\hat{x}\) 展开, 所以 \(x = \hat{x}\) 一阶导是 0,用曲率去估计方差是 \(\hat{\sigma}^2 = -1/\frac{\partial^2 \log g(\hat{x})}{2\partial x^2}\),再重写上述近似 \[ \log g(x) \approx \log g(\hat{x}) - \frac{1}{2\hat{\sigma}^2} (x - \hat{x})^2 \] 现在,用这个结果做正态近似,将上式两端先取指数,再积分,移去常数项 \[ \int g(x) \mathrm{d}x = \int \exp[\log g(x)] \mathrm{d}x \approx \mathrm{constant} \int \exp[- \frac{(x - \hat{x})^2}{2\hat{\sigma}^2}] \mathrm{d}x \] 则拉普拉斯方法近似任意密度函数 \(g(x)\) 得到的正态分布的均值为 \(\hat{x}\), \(\hat{x}\) 可以通过求解方程 \(g'(x) = 0\) 获得,方差为 \(\hat{\sigma}^2 = -1/g''(\hat{x})\)。下面以卡方分布 \(\chi^2\) 为例,由于 \[\begin{align*} &{} f(x; k) = \frac{ x^{k/2-1} \mathrm{e}^{-x/2} }{ 2^{k/2}\Gamma(k/2) }, x \geq 0 \quad \log f(x) = (k/2 - 1) \log x - x/2 \\ &{} \log f'(x) = (k/2-1)/x - 1/2 = 0 \\ &{} \log f''(x) = -(k/2-1)/x^2 \end{align*}\] 所以,卡方分布的拉普拉斯近似为 \[ \chi_{k}^2 \overset{LA}{\sim} \mathcal{N}(\hat{x} = k-2, \hat{\sigma}^2 = 2(k-2)) \] 且自由度越大,近似效果越好,对于多元分布的情况不难推广,使用多元泰勒展开和黑塞矩阵即可表示(Tierney and Kadane 1986)。
4.4 参数估计的算法
4.4.1 拉普拉斯近似极大似然算法
为描述拉普拉斯近似极大似然算法,空间广义线性混合效应模型的结构重新表述如下:
\[\begin{equation} \begin{aligned} \mathbf{Y(x)} | S(\mathbf{x}) & \sim f(\cdot;\boldsymbol{\mu(x)},\psi) \\ g(\boldsymbol{\mu}(\mathbf{x})) & = D\boldsymbol{\beta} + S(\mathbf{x}) = D\boldsymbol{\beta} + \sigma R(\mathbf{x};\phi) + \tau z \\ S(\mathbf{x}) & \sim \mathcal{N}(\mathbf{0},\Sigma) \end{aligned} \tag{4.7} \end{equation}\]
SGLMM 模型假定在给定高斯空间过程 \(S(\mathbf{x})\) 的条件下, \(Y_1,Y_2,\ldots,Y_n\) 是独立的,并且服从分布 \(f(\cdot;\boldsymbol{\mu}(\mathbf{x}),\psi)\)。此分布的参数有两个来源,其一是与联系函数 \(g\) 关联的线性预测 \(\boldsymbol{\mu}(\mathbf{x})\),其二是密度分布函数 \(f\) 的发散参数 \(\psi\),可以看作是似然函数中的附加参数。空间过程 \(S(\mathbf{x})\) 分解为空间相关 \(R(\mathbf{x};\phi)\) 和独立过程 \(Z\),二者分别被参数 \(\sigma\) 和 \(\tau\) 归一化而具有单位方差。线性预测包含一组固定效应 \(D\boldsymbol{\beta}\),空间相关的随机效应 \(R(\mathbf{x};\phi)\),与空间不相关的随机效应 \(\tau z \sim \mathcal{N}(\mathbf{0},\tau^2\mathbf{I})\)。\(D\) 是根据协变量观测值得到的数据矩阵,\(\boldsymbol{\beta}\) 是 \(p \times 1\) 维的回归参数向量。
\(R(\mathbf{x};\phi)\) 是具有单位方差的平稳空间高斯过程,其自相关函数为 \(\rho(u,\phi)\),这里 \(u\) 表示一对空间位置之间的距离,\(\phi\) 是刻画空间相关性的参数。自相关函数 \(\rho(u,\phi) (\in \mathbb{R}^d)\) 是 \(d\) 维空间到一维空间的映射函数,特别地,假定空间过程 \(S(\mathbf{x})\)的自相关函数仅仅依赖成对点之间的欧氏距离,即 \(u =\|x_i - x_j\|\)。常见的自相关函数有指数型、梅隆型和球型。线性预测的随机效应部分协方差矩阵 \(\Sigma = \sigma^2 R(\mathbf{x};\phi) + \tau^2\mathbf{I}\)。
估计 SGLMM 模型 (4.7) 的参数 \(\boldsymbol{\theta} = (\boldsymbol{\beta},\sigma^2,\tau^2,\phi,\psi)\) 需要极大化边际似然函数
\[\begin{equation} L(\boldsymbol{\theta};\mathbf{y}) = \int_{\mathbb{R}^n} [\mathbf{Y(x)}|S(\mathbf{x})][S(\mathbf{x})]\mathrm{d}S(\mathbf{x}) \tag{4.8} \end{equation}\]
边际似然函数 \(L(\boldsymbol{\theta};\mathbf{y})\) 包含两个分布的乘积和随机效应的积分,并且这个积分无法显式的表示,第一个分布是观测变量 \(\mathbf{Y}\) 的抽样分布,第二个分布是多元高斯分布。一个特殊的情况是 \(\mathbf{Y}\) 也假设服从多元高斯分布,这时积分有显式表达式。
边际似然函数 (4.8) 卷入的数值积分是充满挑战的,因为积分的维数 \(n\) 是观测值的数目,所以像二次、高斯-埃尔米特或适应性高斯-埃尔米特数值积分方式都是不可用的,Tierney 和 Kadane (1986 年)提出拉普拉斯近似方法 (Tierney and Kadane 1986),它在纵向数据分析中被大量采用 (Peter J. Diggle et al., n.d.)。总之,对空间广义线性混合效应模型而言,拉普拉斯近似还可以继续采用,想法是近似边际似然函数中的高维 \((n > 3)\) 积分,获得一个易于处理的表达式,有了积分的显式表达式,就可以用数值的方法求边际似然函数的极大值。拉普拉斯方法即用如下方式近似 (4.8) 中的积分
\[\begin{equation} I = \int_{\mathbb{R}^n} \exp\{Q(\mathbf{s})\}\mathrm{d}\mathbf{s} \approx (2\pi)^{n/2} |-Q''(\hat{\mathbf{s}})|^{-1/2}\exp\{Q(\hat{\mathbf{s}})\} \tag{4.9} \end{equation}\]
其中,\(Q(\mathbf{s})\) 为已知的 \(n\) 元函数,\(\hat{\mathbf{s}}\) 是其极大值点,\(Q''(\hat{\mathbf{s}})\) 是黑塞矩阵。拉普拉斯近似的一维情形和主要近似的想法已在第2章第4.3节详细阐述。
拉普拉斯近似方法也可以用于一般的广义线性混合效应模型的似然推断,特别地,对于空间广义线性混合效应模型,假定条件分布 \(f\) 可以表示成如下指数族的形式
\[\begin{equation} f(\mathbf{y};\boldsymbol{\beta}) = \exp\{\mathbf{y}^{\top} (D\boldsymbol{\beta} + S(\mathbf{x})) - \mathbf{1}^{\top} b( D\boldsymbol{\beta} + S(\mathbf{x})) + \mathbf{1}^{\top} c(\mathbf{y}) \} \tag{4.10} \end{equation}\]
其中 \(b(\cdot)\) 是特定的函数,常用的分布有泊松分布和二项分布等,详见第2章第2.1节。把 (4.8) 式中关于 \([S(\mathbf{x})]\) 多元高斯密度函数表示为
\[\begin{align} f(S(\mathbf{x});\Sigma) & = (2\pi)^{-n/2}|\Sigma|^{-1/2} \exp\{ -\frac{1}{2}S(\mathbf{x})^{\top} \Sigma^{-1} S(\mathbf{x}) \} \\ & = \exp\{ - \frac{n}{2}\log (2\pi) -\frac{1}{2}\log |\Sigma| -\frac{1}{2}S(\mathbf{x})^{\top} \Sigma^{-1} S(\mathbf{x}) \} \tag{4.11} \end{align}\]
现在将边际似然函数 (4.8) 写成适合使用拉普拉斯近似的格式
\[\begin{equation} L(\boldsymbol{\theta};\mathbf{y}) = \int_{\mathbb{R}^n} \exp\{Q(S(\mathbf{x}))\} \mathrm{d}S(\mathbf{x}) \end{equation}\]
其中
\[\begin{equation} \begin{aligned} Q(S(\mathbf{x})) ={} & \mathbf{y}^{\top} (D \boldsymbol{\beta} + S(\mathbf{x})) - \mathbf{1}^{\top} b(D \boldsymbol{\beta} + S(\mathbf{x})) + \mathbf{1}^{\top}c(\mathbf{y}) \\ & - \frac{n}{2}\log (2\pi) -\frac{1}{2}\log |\Sigma| -\frac{1}{2}S(\mathbf{x})^{\top} \Sigma^{-1} S(\mathbf{x}) \end{aligned} \tag{4.12} \end{equation}\]
方程 (4.12) 凸显了采纳拉普拉斯近似方法拟合空间广义线性混合效应模型的方便性,可以把 (4.12) 当成两部分来看,前一部分是广义线性模型下样本的对数似然的和的形式,后一部分是多元高斯分布的对数似然。要使用 (4.9) 式,需要函数 \(Q(S(\mathbf{x}))\) 的极大值点 \(\hat{\mathbf{s}}\),这里采用牛顿-拉夫森算法 (Newton-Raphson,简称 NR) 寻找 \(n\) 元函数的极大值点,NR 算法需要重复计算
\[\begin{equation} \mathbf{s}_{i+1} = \mathbf{s}_{i} - Q''(\mathbf{s}_{i})^{-1}Q'(\mathbf{s}_{i}) \end{equation}\]
一直收敛到 \(\hat{\mathbf{s}}\)。在这个内迭代的过程中,将参数 \(\boldsymbol{\theta}\) 当作已知的。\(Q\) 函数的一阶和二阶导数如下
\[\begin{align} Q'(\mathbf{s})& = \{\mathbf{y} - b'(D\boldsymbol{\beta} + \mathbf{s}) \}^{\top} - \mathbf{s}^{\top}\Sigma^{-1} \tag{4.13} \\ Q''(\mathbf{s})& = -\mathrm{diag} \{b''(D\boldsymbol{\beta} + \mathbf{s}) \} - \Sigma^{-1} \tag{4.14} \end{align}\]
用拉普拉斯方法近似的对数似然\(\ell(\boldsymbol{\theta};\mathbf{y})\)
\[\begin{equation} \begin{aligned} \ell(\boldsymbol{\theta};\mathbf{y}) = {} & \frac{n}{2}\log (2\pi) -\frac{1}{2}\log | -\mathrm{diag} \{b''(D\boldsymbol{\beta} + \mathbf{s}) \} - \Sigma^{-1} | \\ & + \mathbf{y}^{\top} (D\boldsymbol{\beta} + \hat{\mathbf{s}}) - \mathbf{1}^{\top} b( D\boldsymbol{\beta} + \hat{\mathbf{s}}) + \mathbf{1}^{\top} c(\mathbf{y}) \\ & - \frac{n}{2}\log (2\pi) -\frac{1}{2}\log |\Sigma| -\frac{1}{2}\hat{\mathbf{s}}^{\top} \Sigma^{-1} \hat{\mathbf{s}} \end{aligned} \tag{4.15} \end{equation}\]
现在极大化近似对数似然 (4.15) 式,此时是求模型参数,可称之为外迭代过程,常用的算法是 Broyden-Fletcher-Goldfarb-Shanno (简称BFGS) 算法,它内置在 R 函数 optim() 中。方便起见,模型参数记为 \(\boldsymbol{\theta} = (\boldsymbol{\beta},\log(\sigma^2),\log(\tau^2),\log(\phi),\log(\psi))\),且 \(\hat{\boldsymbol{\theta}}\) 表示 \(\boldsymbol{\theta}\) 的最大似然估计,根据第2章第2.3节定理2.3,则 \(\hat{\boldsymbol{\theta}}\) 的渐进分布为
\[ \hat{\boldsymbol{\theta}} \sim \mathcal{N}(\boldsymbol{\theta}, \mathbf{I}_{o}^{-1}(\hat{\boldsymbol{\theta}})) \]
其中 \(\mathbf{I}_{o}(\hat{\boldsymbol{\theta}})\) 为观察到的样本信息阵,注意到在空间广义线性混合效应模型下,不能直接计算 Fisher 信息阵,因为对数似然函数没有显式表达式,只有数值迭代获得在 \(\hat{\boldsymbol{\theta}}\) 处的观测信息矩阵。通常,这类渐进近似对协方差参数 \(\sigma^2, \tau^2, \phi\) 的估计效果不好,在数据集不太大的情形下,可用第 4.2 节介绍的剖面似然方法计算协方差参数及其置信区间。剖面似然估计的算法实现过程详见 Bolker 等 (2017年) 开发的 bbmle 包 (Bolker and R Development Core Team 2017),下面给出计算的细节步骤:
- 选择模型参数 \(\boldsymbol{\theta}\) 的初始值 \(\boldsymbol{\theta}_{i}\);
- 计算协方差矩阵 \(\Sigma\) 及其逆 \(\Sigma^{-1}\);
- 通过如下步骤极大\(Q\)函数,获得估计值 \(\hat{\mathbf{s}}\);
- 用 \(\hat{\mathbf{s}}\) 替换 \(S(\mathbf{x})\),在 (4.12) 式中计算 \(Q(\hat{\mathbf{s}})\);
- 用 (4.9) 式计算积分的近似值,以获得边际似然 (4.15) 式的值;
- 用 BFGS 算法获得下一个值 \(\boldsymbol{\theta}_{i+1}\);
- 重复上述过程直到收敛,获得参数的估计值 \(\hat{\boldsymbol{\theta}}\)。
NR算法收敛速度是很快的,但是必须提供一个很好的初值,好的初值对于快速收敛到似然函数 \(\ell(\boldsymbol{\theta};\mathbf{y})\) 的极大值点很重要。指定外迭代中的初值 \(\boldsymbol{\theta}_{0}\)的一个策略是首先拟合一个简单的广义线性模型,获得回归系数 \(\boldsymbol{\beta}\) 的初值,基于这些值计算线性预测值 \(\hat{\boldsymbol{\mu}}\);然后计算残差 \(\hat{\boldsymbol{r}} = (\hat{\boldsymbol{\mu}} - \mathbf{y})\), \(\hat{\boldsymbol{r}}\) 的方差作为 \(\sigma^2\) 的初值,如果 SGLMM 带有块金效应,就用 \(\sigma^2\) 的初值的一定比例,如 10% 作为 \(\tau^2\) 的初值;最后,\(\phi\) 的初值选择两个距离最大的观测点之间的距离的 10%,比较保险的办法是选择不同的 \(\phi\) 作为初值,这个过程需要不断的试错以期获得算法的收敛(Bonat and Ribeiro Jr. 2016)。
4.4.2 蒙特卡罗极大似然算法
为描述蒙特卡罗极大似然算法,空间广义线性混合效应模型的结构表述如下
\[\begin{equation} g(\mu_i) = T_{i} = d(x_i)^{\top}\boldsymbol{\beta} + S(x_i) + Z_i \tag{4.16} \end{equation}\]
其中,令 \(d_{i} = d(x_i)^{\top}\),用\(d(x_i)^{\top}\) 表示 主要是强调协变量的空间内容, 这里表示采样点处观测数据向量, 即 \(p\) 个协变量在第 \(i\) 个位置 \(x_i\) 的观察值。 \(\mathcal{S} = \{S(x): x \in \mathbb{R}^2\}\) 是均值为 \(\mathbf{0}\),方差为 \(\sigma^2\),平稳且各向同性的空间高斯过程,自相关函数是 \(\rho(u;\phi)\),\(S(x_i)\) 表示空间效应,\(Z_i \stackrel{i.i.d}{\sim} \mathcal{N}(0,\tau^2)\) 的块金效应,\(g\) 是联系函数,\(x_i \in \mathbb{R}^2\)是采样点的位置。 综上,模型 (4.16) 待估计的参数有 \(\boldsymbol{\beta}\) 和 \(\boldsymbol{\theta}' = (\sigma^2,\phi,\tau^2)\)。 特别地,当响应变量分别服从二项分布和泊松分布时, 模型 (4.16) 分别变为模型 (4.17) 和模型 (4.18)。 \[\begin{align} \log\{\frac{p_i}{1-p_i}\} & = T_{i} = d(x_i)^{\top}\boldsymbol{\beta} + S(x_i) + Z_i \tag{4.17}\\ \log(\lambda_i) & = T_{i} = d(x_i)^{\top}\boldsymbol{\beta} + S(x_i) + Z_i \tag{4.18} \end{align}\] 模型 (4.17) 中,响应变量 \(Y_i\) 服从二项分布 \(Y_i \sim \mathrm{Binomial}(m_i,p_i)\), 均值 \(\mathsf{E}(Y_i|S(x_i),Z_i)=m_{i}p_{i}\), \(m_i\) 表示在 \(x_i\) 的位置抽取的样本量,总的样本量就是 \(M = \sum_{i=1}^{N}m_i\),\(N\) 表示采样点的个数。模型 (4.18) 中, 响应变量 \(Y_i\) 服从泊松分布 \(Y_i \sim \mathrm{Poisson}(\lambda_i)\)。 在获取响应变量 \(Y\) 的观测的过程中,与广义线性或广义线性混合效应模型 (3.2) 和 (3.3) 不同的在于:在每个采样点 \(x_i\) 处,\(Y_i\) 都服从参数不同但同类的分布。
模型 (4.17) 中参数 \(\boldsymbol{\beta}\) 和 \(\boldsymbol{\theta}^{\top} = (\sigma^2,\phi,\tau^2)\) 的似然函数是通过对 \(T_i\) 内的随机效应积分获得的。 用大写 \(D\) 表示 \(n\times p\) 的数据矩阵, \(y = (y_1, y_2,\cdots, y_n)\) 表示各空间位置 \(x_i\) 处响应变量的观测值,对应模型 (4.17) 中的 \(Y_i \sim \mathrm{Binomial}(m_i,p_i)\), \(\mathbf{T} = (T_1,T_2,\ldots,T_n)\) 的边际分布是 \(\mathcal{N}(D\boldsymbol{\beta}, \Sigma(\boldsymbol{\theta}))\), 其中,协方差矩阵 \(\Sigma(\boldsymbol{\theta})\) 的对角元是 \(\sigma^2+\tau^2\), 非对角元是 \(\sigma^2\rho(u_{ij})\), \(u_{ij}\) 是位置 \(x_i\) 与 \(x_j\) 之间的距离。在给定 \(\mathbf{T} = t = (t_1,t_2,\cdots,t_n)\) 下, \(\mathbf{Y} = y =(y_1,\cdots,y_n)\) 的条件分布是独立二项概率分布函数的乘积 \(f(y|t)=\prod_{i=1}^{n}f(y_{i}|t_{i})\), 因此, \(\boldsymbol{\beta}\) 和 \(\boldsymbol{\theta}\) 的似然函数可以写成
\[\begin{equation} L(\boldsymbol{\beta},\boldsymbol{\theta}) = f(y;\boldsymbol{\beta},\boldsymbol{\theta}) = \int_{\mathbb{R}^{n}}\mathcal{N}(t;D\boldsymbol{\beta},\Sigma(\boldsymbol{\theta}))f(y|t)dt \tag{4.19} \end{equation}\]
其中\(\mathcal{N}(\cdot;\mu,\Sigma)\) 表示均值为 \(\mu\),协方差矩阵为 \(\Sigma\) 的多元高斯分布的密度函数。Geyer (1994 年)(Geyer 1994) 在给定 \(\mathbf{Y}=y\) 的情况下,使用 \(\mathbf{T}\) 的条件分布 \(f(\mathbf{T}|\mathbf{Y}=y)\) 模拟近似方程 (4.19) 中的高维积分,则似然函数 \(L(\boldsymbol{\beta},\boldsymbol{\theta})\) 可以重写为
\[\begin{equation} \begin{aligned} L(\boldsymbol{\beta},\boldsymbol{\theta}) & = \int_{\mathbb{R}^{n}} \frac{\mathcal{N}(t;D\boldsymbol{\beta},\Sigma(\boldsymbol{\theta}))f(y|t)}{\mathcal{N}(t;D\boldsymbol{\beta}_{0},\Sigma(\boldsymbol{\theta}_{0}))f(y|t)}f(y,t)dt \\ & \varpropto \int_{\mathbb{R}^{n}} \frac{\mathcal{N}(t;D\boldsymbol{\beta}, \Sigma(\boldsymbol{\theta}))}{\mathcal{N}(t;D\boldsymbol{\beta}_{0}, \Sigma(\boldsymbol{\theta}_{0}))}f(t|y)dt \\ &= E_{T|y}\left[\frac{\mathcal{N}(t; D\boldsymbol{\beta}, \Sigma(\boldsymbol{\theta}))}{\mathcal{N}(t; D\boldsymbol{\beta}_{0}, \Sigma(\boldsymbol{\theta}_{0}))}\right] \end{aligned} \tag{4.20} \end{equation}\]
其中 \(\boldsymbol{\beta}_{0},\boldsymbol{\theta}_{0}\) 作为迭代初始值预先给定,则 \(Y\) 和 \(T\) 的联合分布可以表示成 \(f(y,t) = \mathcal{N}(t; D\boldsymbol{\beta}_{0}, \Sigma(\boldsymbol{\theta}_{0})) f(y|t)\)。通过蒙特卡罗方法,用求和代替积分近似期望, 做法是从条件分布 \(f(T|Y=y; \boldsymbol{\beta}_0, \boldsymbol{\theta}_0)\) 抽取 \(m\) 个样本 \(t_{(i)}\), 那么,可以用方程 (4.21) 近似方程 (4.20)
\[\begin{equation} L_{m}(\boldsymbol{\beta},\boldsymbol{\theta})=\frac{1}{m}\sum_{i=1}^{n}\frac{\mathcal{N}(t_{i};D\boldsymbol{\beta},\Sigma(\boldsymbol{\theta}))}{\mathcal{N}(t_{i};D\boldsymbol{\beta}_{0},\Sigma(\boldsymbol{\theta}_{0}))} \tag{4.21} \end{equation}\]
这样做的依据是不管样本序列 \(t_{(i)}\) 是否相关, \(L_{m}(\boldsymbol{\beta},\boldsymbol{\theta})\) 都是 \(L_{m}(\boldsymbol{\beta},\boldsymbol{\theta})\) 的一致估计 (consistent estimator)(Giorgi and Diggle 2017)。 最优的 \(\boldsymbol{\beta}_0,\boldsymbol{\theta}_0\) 是 \(\boldsymbol{\beta},\boldsymbol{\theta}\) 的极大似然估计,即
\[ \max_{\boldsymbol{\beta},\boldsymbol{\theta}}L_{m}(\boldsymbol{\beta},\boldsymbol{\theta}) \rightarrow 1, m \rightarrow\infty \]
既然初始值 \(\boldsymbol{\beta}_{0},\boldsymbol{\theta}_{0}\) 与真实的极大似然估计值不同,可以用第 \(m\) 步迭代获得的似然函数值 \(L_{m}(\hat{\boldsymbol{\beta}}_{m}, \hat{\boldsymbol{\theta})}_{m}\) 与 1 的距离来刻画蒙特卡罗近似的准确度。实际操作中,用 \(\hat{\boldsymbol{\beta}}_{m}\) 和 \(\hat{\boldsymbol{\theta}}_{m}\) 表示最大化 \(L_{m}(\boldsymbol{\beta}, \boldsymbol{\theta})\) 获得的 MCML 估计,重复迭代 \(\boldsymbol{\beta}_{0} = \hat{\boldsymbol{\beta}}_{m}\) 和 \(\boldsymbol{\theta}_{0} = \hat{\boldsymbol{\theta}}_{m}\) 直到收敛。 求蒙特卡罗近似的对数似然 \(l_{m}(\boldsymbol{\beta}, \boldsymbol{\theta}) = \log L_{m}(\boldsymbol{\beta}, \boldsymbol{\theta})\) 的极值,可以使用 PrevMap 包,迭代 \(L_{m}(\boldsymbol{\beta}, \boldsymbol{\theta})\) 的过程中,可以选择 BFGS 算法。由于 \(\boldsymbol{\psi}\) 的似然曲面是相当扁平的,为了更好的收敛,做一步重参数化,即令 \(\boldsymbol{\psi} = \log(\boldsymbol{\theta})\),\(L_{m}(\boldsymbol{\beta}, \boldsymbol{\psi})\) 关于 \(\boldsymbol{\beta}\) 和 \(\boldsymbol{\psi}\) 的一阶、二阶导数传递给 maxLik 包的 maxBFGS 函数。蒙特卡罗极大似然估计 \(\boldsymbol{\theta}_{m}\) 的标准误差 (standard errors) 取似然函数 \(l_{m}(\boldsymbol{\beta},\boldsymbol{\theta})\) 的负黑塞矩阵的逆的对角线元素的平方根。迭代次数足够多时,即 \(m\) 充分大时,一般取到 10000 及以上,此时蒙特卡罗误差可忽略,即用方程 (4.21) 近似 (4.20) 的误差可忽略。
4.4.3 贝叶斯 Langevin-Hastings 算法
在贝叶斯框架里,\(\boldsymbol{\beta}, \boldsymbol{\theta}\) 的后验分布由贝叶斯定理和 \(\boldsymbol{\beta}, \boldsymbol{\theta}\) 的联合先验分布确定,见第2章基础知识第2.5节后验分布的推导。假定 \(\boldsymbol{\beta}, \boldsymbol{\theta}\) 的先验分布如下: \[ \boldsymbol{\theta} \sim g(\cdot), \quad \boldsymbol{\beta} | \sigma^2 \sim \mathcal{N}(\cdot; \xi, \sigma^2 \Omega) \] 其中 \(g(\cdot)\) 可以是 \(\boldsymbol{\theta}\) 的任意分布,\(\xi\) 和 \(\Omega\) 分别是 \(\boldsymbol{\beta}\) 的高斯先验的均值向量和协方差矩阵。则\(\boldsymbol{\beta}, \boldsymbol{\theta}\) 和 \(\mathbf{T}\) 的后验分布是
\[\begin{equation} \pi(\boldsymbol{\beta}, \boldsymbol{\theta}, t | y) \propto g(\boldsymbol{\theta})\mathcal{N}(\boldsymbol{\beta}; \xi, \sigma^2 \Omega)\mathcal{N}(t; D\boldsymbol{\beta}, \Sigma(\boldsymbol{\theta}))f(y|t) \tag{4.22} \end{equation}\]
R 包 PrevMap 内的函数 binomial.logistic.Bayes 可以从上述后验分布中抽得样本,这个抽样的过程使用了 MCMC 算法, \(\boldsymbol{\theta}, \boldsymbol{\beta}\) 和 \(\mathbf{T}\) 轮流迭代的过程如下:
- 初始化\(\boldsymbol{\beta}, \boldsymbol{\theta}\) 和\(\mathbf{T}\);
- 对协方差\(\Sigma(\boldsymbol{\theta})\)中的参数做如下变换 (Christensen, Roberts, and Sköld 2006) \[(\tilde{\theta}_{1}, \tilde{\theta}_{2}, \tilde{\theta}_{3}) = (\log \sigma, \log (\sigma^2/\phi^{2\kappa}), \log \tau^2)\] 使用随机游走 Metropolis-Hastings 算法轮流更新上述三个参数,在第 \(i\) 次迭代时,候选高斯分布的标准差 \(h\) 是 \(h_{i} = h_{i-1} + c_{1}i^{-c_{2}}(\alpha_{i}-0.45)\),其中,\(c_{1} > 0\) 和 \(c_{2} \in (0,1]\) 是预先给定的常数,\(\alpha_i\) 是第 \(i\) 次迭代时的接受概率,其中 0.45 是一元高斯分布的最优接受概率;
- 使用Gibbs步骤更新 \(\boldsymbol{\beta}\), 所需条件分布 \(\boldsymbol{\beta}|\boldsymbol{\theta},\mathbf{T}\) 是高斯分布,均值 \(\tilde{\xi}\),协方差矩阵 \(\sigma^2\tilde{\Omega}\),且与 \(y\) 不相关,记\(\Sigma(\boldsymbol{\theta}) = \sigma^2 R(\boldsymbol{\theta})\) \[ \tilde{\xi} = \tilde{\Omega}(\Omega^{-1}\xi+D^{\top} R(\boldsymbol{\theta})^{-1} \mathbf{T}), \quad \sigma^2 \tilde{\Omega} = \sigma^2(\Omega^{-1} + D^{\top} R(\boldsymbol{\theta})^{-1} D)^{-1} \]
- 使用汉密尔顿蒙特卡罗算法更新条件分布 \(\mathbf{T}|\boldsymbol{\beta},\boldsymbol{\theta},y\),用 \(H(t,u)\) 表示汉密尔顿函数 \[H(t, u) = u^{\top} u/2 - \log f(t | y, \boldsymbol{\beta}, \boldsymbol{\theta})\] 其中,\(u\in\mathbb{R}^2\), \(f(t | y, \boldsymbol{\beta}, \boldsymbol{\theta})\) 表示给定 \(\boldsymbol{\beta}\), \(\boldsymbol{\theta}\) 和 \(y\)下,\(\mathbf{T}\) 的条件分布。根据汉密尔顿方程,函数 \(H(u, t)\) 的偏导决定 \(u,t\) 随时间 \(v\) 的变化过程, \[\begin{eqnarray*} \frac{d t_{i}}{d v} & = & \frac{\partial H}{\partial u_{i}} \\ \frac{d u_{i}}{d v} & = & -\frac{\partial H}{\partial t_{i}} \end{eqnarray*}\] 其中,\(i = 1,\ldots, n\), 上述动态汉密尔顿微分方程根据 leapfrog 方法(Brooks et al. 2011)离散, 然后求解离散后的方程组获得近似解。
4.4.4 低秩近似算法
低秩近似算法分两部分来阐述,第一部分讲空间高斯过程的近似,第二部分将该近似方法应用于 SGLMM 模型。
空间高斯过程 \(\mathcal{S} = \{S(x),x\in\mathbb{R}^2\}\) 对任意给定一组空间位置 \(x_1,x_2,\ldots,x_n, \forall x_{i} \in \mathbb{R}^2\),随机变量 \(S(x_i),i = 1,2,\ldots,n\) 的联合分布 \(\mathcal{S}=\{S(x_1),S(x_2),\ldots,S(x_n)\}\) 是多元高斯分布,其由均值 \(\mu(x) = \mathsf{E}[S(x)]\) 和协方差 \(G_{ij} =\gamma(x_i,x_j)= \mathsf{Cov}\{S(x_i),S(x_j)\}\) 完全确定,即 \(\mathcal{S} \sim \mathcal{N}(\mu_{S},G)\)。
低秩近似算法使用奇异值分解协方差矩阵 \(G\) (Peter J. Diggle and Ribeiro Jr., n.d.), 将协方差矩阵 \(G\) 分解,也意味着将空间高斯过程 \(\mathcal{S}\) 分解,令 \[\mathcal{S} = AZ\] 其中,\(A = U\Lambda^{1/2}\),对角矩阵 \(\Lambda\) 包含 \(G\) 的所有特征值,\(U\) 是特征值对应的特征向量。将特征值按从大到小的顺序排列,取 \(A\) 的前 \(m(<n)\) 列,即可获得 \(\mathcal{S}\) 的近似 \(\mathcal{S}^{\star}\), \[\begin{equation} \mathcal{S}^{\star} = A_{m}Z \tag{4.23} \end{equation}\] 现在,\(Z\) 只包含 \(m\) 个相互独立的标准正态随机变量。方程 (4.23) 可以表示成 \[\begin{equation} \mathcal{S}^{\star} = \sum_{j=1}^{m}Z_{j}f_{j}(x_{i}), i = 1,2,\ldots,n \tag{4.24} \end{equation}\] 不难看出,方程(4.24)不仅是 \(\mathcal{S}\) 的低秩近似,还可用作为空间高斯过程 \(\mathcal{S}\) 的定义。 更一般地,空间连续的随机过程 \(S(x)\) 都可以表示成函数 \(f_{j}(x)\) 和随机系数 \(A_{j}\) 的线性组合。 \[\begin{equation} S(x) = \sum_{j=1}^{m}A_{j}f_{j}(x), \forall x \in \mathbb{R}^2 \tag{4.25} \end{equation}\] 若 \(A_j\) 服从零均值,协方差为 \(\mathsf{Cov}(A_{j},A_{k})=\gamma_{jk}\) 的多元高斯分布,则 \(\mathcal{S}\) 均值为0,协方差为 \[\begin{equation} \mathsf{Cov}(S(x),S(x')) = \sum_{j=1}^{m}\sum_{k=1}^{m}\gamma_{jk}f_{j}(x)f_{k}(x') \tag{4.26} \end{equation}\] 一般情况下,协方差结构 (4.26) 不是平稳的,其中,\(f_{k}(\cdot)\) 来自一组正交基 \[\begin{equation*} \int f_{j}(x)f_{k}(x)dx = \begin{cases} 1, & i \neq j \\ 0, & i = j \end{cases} \end{equation*}\] 随机系数 \(A_{j}\) 满足相互独立。
为方便叙述起见,低秩近似算法以模型 (4.27) 为描述对象,它是模型 (4.16) 的特殊形式,主要区别是模型 (4.27) 中,联系函数 \(g(\mu) = \log\big(\frac{\mu}{1-\mu}\big)\)
\[\begin{equation} \log\{\frac{p_i}{1-p_i}\} = T_{i} = d(x_i)^{\top}\boldsymbol{\beta} + S(x_i) + Z_{i} \tag{4.27} \end{equation}\]
模型 (4.27) 中的高斯过程 \(\mathcal{S} = S(x)\) 可以表示成高斯噪声的卷积形式
\[\begin{equation} S(x) = \int_{\mathbb{R}^2} K(\|x-t\|; \phi, \kappa) \: d B(t) \tag{4.28} \end{equation}\]
其中,\(B\) 表示布朗运动,\(\|\cdot\|\) 表示欧氏距离,\(K(\cdot)\) 表示自相关函数,其形如
\[\begin{equation} K(u; \phi, \kappa) = \frac{\Gamma(\kappa + 1)^{1/2}\kappa^{(\kappa+1)/4}u^{(\kappa-1)/2}}{\pi^{1/2}\Gamma((\kappa+1)/2)\Gamma(\kappa)^{1/2}(2\kappa^{1/2}\phi)^{(\kappa+1)/2}}\mathcal{K}_{\kappa}(u/\phi), u > 0 \tag{4.29} \end{equation}\]
将方程 (4.28)离散化,且让 \(r\) 充分大,以获得低秩近似 (Giorgi and Diggle 2017)
\[\begin{equation} S(x) \approx \sum_{i = 1}^r K(\|x-\tilde{x}_{i}\|; \phi, \kappa) U_{i} \tag{4.30} \end{equation}\]
式(4.30)中, \((\tilde{x}_{1},\ldots,\tilde{x}_{r})\) 表示空间网格的格点,\(U_{i}\) 是独立同分布的高斯变量,均值为\(0\), 方差为\(\sigma^2\)。 特别地, 尺度参数\(\phi\)越大时,空间曲面越平缓,如图 3.3所示,在格点数 \(r\) 比较少时也能得到不错的近似效果。 此外, 空间格点数 \(r\) 与样本量 \(n\) 是独立的, 因此, 低秩近似算法在样本量比较大时, 计算效率还比较高。
注意到平稳空间高斯过程 \(S(x)\) 经过方程 (4.30) 的近似已不再平稳。通过乘以 \[\frac{1}{n}\sum_{i = 1}^n \sum_{j = 1}^m K(\|\tilde{x}_{j}-\tilde{x}_{i}\|; \phi, \kappa)^2\] 来调整 \(\sigma^2\)。 事实上,调整后的 \(\sigma^2\) 会更接近于高斯过程 \(S(x)\) 的实际方差。
低秩近似的关键是对高斯过程 \(\mathcal{S}\) 的协方差矩阵 \(\Sigma(\boldsymbol{\theta})\) 做降维分解, 这对 \(\Sigma(\boldsymbol{\theta})\) 的逆和行列式运算是非常重要的,在计算之前,将 \(K(\boldsymbol{\theta})\) 表示为 \(n\times r\) 的核矩阵,它是由自协方差函数决定的空间距离矩阵,协方差矩阵 \(\Sigma(\boldsymbol{\theta}) = \sigma^2K(\boldsymbol{\theta})K(\boldsymbol{\theta})^{\top}+\tau^2 I_{n}\),\(I_{n}\) 是 \(n\times n\) 的单位矩阵。根据 Woodbury 公式可得 \[\Sigma(\boldsymbol{\theta})^{-1} = \sigma^2\nu^{-2}(I_{n}-\nu^{-2}K(\boldsymbol{\theta})(\nu^{-2}K(\boldsymbol{\theta})^{\top} K(\boldsymbol{\theta})+I_{r})^{-1}K(\boldsymbol{\theta})^{\top})\] 其中, \(\nu^2 = \tau^2/\sigma^2\),求 \(n\) 阶方阵 \(\Sigma(\boldsymbol{\theta})\) 的逆变成求 \(r\) 阶方阵的逆, 从而达到了降维的目的。 下面再根据 Sylvester 行列式定理计算 \(\Sigma(\boldsymbol{\theta})\) 的行列式 \(|\Sigma(\boldsymbol{\theta})|\) \[\begin{eqnarray*} |\Sigma(\boldsymbol{\theta})| & = & |\sigma^2K(\boldsymbol{\theta})K(\boldsymbol{\theta})^{\top}+\tau^2 I_{n}| \\ & = & \tau^{2n}|\nu^{-2}K(\boldsymbol{\theta})^{\top} K(\boldsymbol{\theta})+I_{r}| \end{eqnarray*}\] 类似地,行列式运算的维数从 \(n\times n\) 降到了 \(r\times r\) (Peter J. Diggle and Ribeiro Jr., n.d.)。
4.5 贝叶斯 Stan-HMC 算法
4.5.1 蒙特卡罗积分
一般地,空间广义线性混合效应模型的统计推断总是不可避免的要面对高维积分,处理高维积分的方法一个是寻找近似方法避免求积分,一个是寻找有效的随机模拟方法直接求积分。这里,介绍蒙特卡罗方法求积分,以计算 \(N\) 维超立方体的内切球的体积为例说明。
假设我们有一个 \(N\) 维超立方体,其中心在坐标 \(\mathbf{0} = (0,\ldots,0)\)。超立方体在点 \((\pm 1/2,\ldots,\pm 1/2)\),有 \(2^{N}\) 个角落,超立方体边长是1,\(1^{N}=1\),所以它的体积是1。如果 \(N=1\),超立方体是一条从 \(-\frac{1}{2}\) 到 \(\frac{1}{2}\) 的单位长度的线,如果 \(N=2\),超立方体是一个单位正方形,对角是 \(\left( -\frac{1}{2}, -\frac{1}{2} \right)\) 和 \(\left( \frac{1}{2}, \frac{1}{2} \right)\),如果 \(N=3\),超立方体就是单位体积的立方体,对角是 \(\left( -\frac{1}{2}, -\frac{1}{2}, -\frac{1}{2} \right)\) 和 \(\left( \frac{1}{2}, \frac{1}{2}, \frac{1}{2} \right)\),依此类推,\(N\) 维超立方体体积是1,对角是 \(\left( -\frac{1}{2}, \ldots, -\frac{1}{2} \right)\) 和 \(\left( \frac{1}{2}, \ldots, \frac{1}{2} \right)\)。
现在,考虑 \(N\) 维超立方体的内切球,我们把它称为 \(N\) 维超球,它的中心在原点,半径是 \(\frac{1}{2}\)。我们说点 \(y\) 在超球内,意味着它到原点的距离小于半径,即 \(\| y \| < \frac{1}{2}\)。一维情形下,超球是从的线,包含了整个超立方体。二维情形下,超球是中心在原点,半径为 \(\frac{1}{2}\) 的圆。三维情形下,超球是立方体的内切球。已知单位超立方体的体积是1,但是其内的内切球的体积是多少呢?我们已经学过如何去定义一个积分计算半径为 \(r\) 的二维球(即圆)的体积(即面积)是 \(\pi r^2\),三维情形下,内切球是 \(\frac{4}{3}\pi r^3\)。但是更高维的欧式空间里,内切球的体积是多少呢?
在这种简单的体积积分设置下,当然可以去计算越来越复杂的多重积分,但是这里介绍采样的方法去计算积分,即所谓的蒙特卡罗方法,由梅特罗波利斯,冯\(\cdot\)诺依曼和乌拉姆等在美国核武器研究实验室创立,当时正值二战期间,为了研制原子弹,出于保密的需要,与随机模拟相关的技术就代号蒙特卡罗。现在,蒙特卡罗方法占据现代统计计算的核心地位,特别是与贝叶斯相关的领域。
用蒙特卡罗方法去计算单位超立方体内的超球,首先需要在单位超立方体内产生随机点,然后计算落在超球内的点的比例,即超球的体积。随着点的数目增加,估计的体积会收敛到真实的体积。因为这些点都独立同均匀分布,根据中心极限定理,误差下降的比率是 \(\mathcal{O}\left( 1 / \sqrt{n} \right)\),这也意味着每增加一个小数点的准确度,样本量要增加 100 倍。
| 维数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 体积 | 1.000 | 0.784 | 0.525 | 0.307 | 0.166 | 0.081 | 0.037 | 0.016 | 0.006 | 0.0027 |
表 4.1 列出了前 10 维超球的体积,从上述计算过程中,我们发现随着维数增加,超球的体积迅速变小。这里有一个反直观的现象,内切球的体积竟然随着维数的增加变小,并且在 10 维的情形下,内切球的体积已不到超立方体的 0.3%,可以预见如果这个积分是 100 维甚至更多,那么内切球相比于正方体仅仅是一个极小的角落,随机点会越来越难以落在内切球内。甚至会因为所需要的随机数太多或者计算机资源的限制,而不可计算,开发更加高效的随机模拟算法也就势在必行。
4.5.2 背景和意义
贝叶斯 MCMC 算法是一个计算密集型的算法,高效的实现对理论和应用都有非常重要的意义。因此,早在 1989 年剑桥大学研究人员开发出了 Windows 上的应用程序 WinBUGS,并被广泛使用。随着个人电脑的普及、Linux 和 MacOS 系统的蓬勃发展, 只能运行于 Windows 系统上的 WinBUGS 逐渐落后于时代,并在 2008 年宣布停止开发。 随后, OpenBUGS 以开源的开发方式重现了 WinBUGS 的功能,还可跨平台运行,弥补了 WinBUGS 的一些不足,而后又出现了同类的开源软件 JAGS。 无论是 OpenBUGS 还是 JAGS 都无法适应当代计算机硬件的迅猛发展, 它们的设计由于历史局限性, 已经无法满足在兼容性、 扩展性和高效性方面的要求。 所以, 哥伦比亚大学的统计系以开源的方式开发了新一代贝叶斯推断子程序库 Stan, 它与前辈们最明显的最直观的不同在于,它不是一个像 WinBUGS/OpenBUGS/JAGS 那样的软件有菜单窗口或软件内的命令行环境, Stan 是一种概率编程语言 (Carpenter et al. 2017), 可以替代 BUGS (Bayesian inference Using Gibbs Sampling) (Lunn et al. 2009) 作为 MCMC 算法的高效实现。相比较于同类软件,Stan 的优势有:底层完全基于 C++ 实现;拥有活跃和快速发展的社区;支持在CPU/GPU上大规模并行计算;独立于系统和硬件平台;提供多种编程语言的接口,如 PyStan、 RStan 等等。 在大数据的背景下, 拥有数千台服务器的企业越来越多, 计算机资源达到前所未有的规模, 这为 Stan 的广泛应用打下了基础。
4.5.3 Stan 简介
在上世纪 40~50 年代,由梅特罗波利斯,冯\(\cdot\)诺依曼和乌拉姆 (Stanislaw Ulam) 创立蒙特卡罗方法,为了纪念乌拉姆,Stan 就以他的名字命名。Stan 是一门基于 C++ 的概率编程语言,主要用于贝叶斯推断,它的代码完全开源的,托管在 Github 上,自 2012 年 8 月 30 日发布第一个 1.0 版本以来,截至写作时间已发布 33 个版本,目前最新版本是 2.18.0。使用 Stan,用户需提供数据、Stan 代码写的脚本模型,编译 Stan 写的程序,然后与数据一起运行,模型参数的后验模拟过程是自动实现的。除了可以在命令行环境下编译运行 Stan 脚本中写模型外,Stan 还提供其他编程语言的接口,如 R、Python、Matlab、Mathematica、Julia 等等,这使得熟悉其他编程语言的用户可以方便地调用和分析数据。但是,与 Python、R等 这类解释型编程语言不同, Stan 代码需要先翻译成 C++ 代码,然后使用系统编译器 (如 GCC) 编译,若使用 R 语言接口,编译后的动态链接库可以载入 R 内存中,再被其他 R 函数调用执行。
随机模拟的前提是有能产生高质量高效的伪随机数发生器,只有周期长,生成速度快,能通过一系列统计检验的伪随机数才能用作统计模拟。Stan 内置了 Mersenne Twister 发生器,它的周期长达 \(2^{19937}-1\),通过了一系列严格的检验,被广泛采用到现代软件中,如 Octave 和 Matlab 等 (黄湘云 2017)。除了 Mersenne Twister 随机数发生器,Stan 还使用了 Boost C++ 和 Eigen C++ 等模版库用于线性代数计算,这样的底层设计路线使得 Stan 的运算效率很高。
Stan 内置的采样器 No-U-Turn (简称 NUTS) 源于汉密尔顿蒙特卡罗算法 (Hamiltonian Monte Carlo,简称 HMC),最早由 Hoffman 和 Gelman (2014年) (Hoffman and Gelman 2014) 提出。与 Stan 有相似功能的软件 BUGS 和 JAGS 主要采用的是 Gibbs 采样器,前者基于 Pascal 语言开发于 1989 年至 2004 年,后者基于 C++ 活跃开发于 2007 年至 2013 年。在时间上, Stan 具有后发优势,特别在灵活性和扩展性方面,它支持任意的目标函数,模型语言也更加简单易于推广学习,其每一行都是命令式的语句,而 BUGS 和 JAGS 采用声明式;在大量数据的建模分析中, Stan 可以更快地处理复杂模型,这一部分归功于它高效的算法实现和内存管理,另一部分在于高级的 MCMC 算法 — 带 NUTS 采样器的 HMC 算法。
Rubin (1981年) (Rubin 1981) 分析了 Alderman 和 Powers (Alderman and Powers 1980) 收集的原始数据,得出表 4.2, Gelman 和 Carlin 等 (2003年) (Gelman et al. 2003) 建立分层正态模型 (4.31) 分析 Eight Schools 数据集,由美国教育考试服务调查搜集,用以分析不同的培训项目对学生考试分数的影响,其随机调查了 8 所高中,学生的成绩作为培训效应的估计 \(y_j\),其样本方差 \(\sigma^2_j\),数据集见表 4.2。这里再次以该数据集和模型为例介绍 Stan 的使用。
\[\begin{equation} \begin{aligned} &{} \mu \sim \mathcal{N}(0,5), \quad \tau \sim \text{Half-Cauchy}(0,5), \quad p(\mu,\tau) \propto 1 \\ &{} \eta_i \sim \mathcal{N}(0,1), \quad \theta_i = \mu + \tau \cdot \eta_i, \quad y_i \sim \mathcal{N}(\theta_i,\sigma^2_{i}), i = 1,\ldots,8 \end{aligned} \tag{4.31} \end{equation}\]
| School | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| \(y_i\) | 28 | 8 | -3 | 7 | -1 | 1 | 18 | 12 |
| \(\sigma_i\) | 15 | 10 | 16 | 11 | 9 | 11 | 10 | 18 |
根据公式组 (4.31) 指定的各参数先验分布,分层正态模型可以在 Stan 中写成四段。第一段提供数据:学校的数目 \(J\),估计值 \(y_1,\ldots,y_{J}\),标准差 \(\sigma_1,\ldots,\sigma_{J}\),数据类型可以是整数、实数,结构可以是向量,或更一般的数组,还可以带约束,如在这个模型中 \(J\) 限制为非负, \(\sigma_{J}\) 必须是正的,另外两个反斜杠 // 表示注释。第二段代码声明参数:模型中的待估参数,学校总体的效应 \(\theta_j\),均值 \(\mu\),标准差 \(\tau\),学校水平上的误差 \(\eta\) 和效应 \(\theta\)。在这个模型中,用 \(\mu,\tau,\eta\) 表示 \(\theta\) 而不是直接声明 \(\theta\) 作一个参数,通过这种参数化,采样器的运行效率会提高,还应该尽量使用向量化操作代替 for 循环语句。最后一段是模型:稍微注意的是,正文中正态分布 \(\mathcal{N}(\cdot,\cdot)\) 中后一个位置是方差,而 Stan 代码中使用的是标准差。target += normal_lpdf(y | theta, sigma) 和 y ~ normal(theta, sigma) 对模型的贡献是一样的,都使用正态分布的对数概率密度函数,只是后者扔掉了对数后验密度的常数项而已,这对于 Stan 的采样、近似和优化算法没有影响。
算法运行的硬件环境是 16 核 32 线程主频 2.8 GHz 英特尔至强 E5-2680 处理器,系统环境 CentOS 7,R 软件版本 3.5.1,RStan 版本 2.17.3。算法参数设置了 4 条迭代链,每条链迭代 10000 次,为复现模型结果随机数种子设为 2018。
分层正态模型(4.31) 的参数 \(\mu,\tau\),及其参数化引入的中间参数 \(\eta_i,\theta_i,i=1,\ldots,8\),还有对数后验 \(\mathrm{lp}\_\_\) 的估计值见表 4.3。
| mean | se_mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| \(\mu\) | 7.99 | 0.05 | 5.02 | -1.65 | 4.75 | 7.92 | 11.15 | 18.10 | 8455 | 1 |
| \(\tau\) | 6.47 | 0.06 | 5.44 | 0.22 | 2.45 | 5.18 | 9.07 | 20.50 | 7375 | 1 |
| \(\eta_1\) | 0.40 | 0.01 | 0.93 | -1.49 | -0.21 | 0.42 | 1.02 | 2.19 | 16637 | 1 |
| \(\eta_2\) | 0.00 | 0.01 | 0.87 | -1.73 | -0.58 | 0.00 | 0.57 | 1.70 | 16486 | 1 |
| \(\eta_3\) | -0.20 | 0.01 | 0.93 | -1.99 | -0.82 | -0.20 | 0.41 | 1.66 | 20000 | 1 |
| \(\eta_4\) | -0.04 | 0.01 | 0.88 | -1.80 | -0.60 | -0.04 | 0.53 | 1.74 | 20000 | 1 |
| \(\eta_5\) | -0.36 | 0.01 | 0.88 | -2.06 | -0.94 | -0.38 | 0.20 | 1.42 | 15489 | 1 |
| \(\eta_6\) | -0.22 | 0.01 | 0.90 | -1.96 | -0.82 | -0.23 | 0.37 | 1.57 | 20000 | 1 |
| \(\eta_7\) | 0.34 | 0.01 | 0.89 | -1.49 | -0.24 | 0.36 | 0.93 | 2.04 | 16262 | 1 |
| \(\eta_8\) | 0.05 | 0.01 | 0.94 | -1.81 | -0.57 | 0.06 | 0.69 | 1.91 | 20000 | 1 |
| \(\theta_1\) | 11.45 | 0.08 | 8.27 | -1.86 | 6.07 | 10.27 | 15.50 | 31.68 | 11788 | 1 |
| \(\theta_2\) | 7.93 | 0.04 | 6.15 | -4.45 | 3.99 | 7.90 | 11.74 | 20.44 | 20000 | 1 |
| \(\theta_3\) | 6.17 | 0.06 | 7.67 | -11.17 | 2.07 | 6.74 | 10.89 | 19.94 | 16041 | 1 |
| \(\theta_4\) | 7.66 | 0.05 | 6.51 | -5.63 | 3.75 | 7.72 | 11.62 | 20.78 | 20000 | 1 |
| \(\theta_5\) | 5.13 | 0.05 | 6.41 | -9.51 | 1.37 | 5.66 | 9.43 | 16.41 | 20000 | 1 |
| \(\theta_6\) | 6.14 | 0.05 | 6.66 | -8.63 | 2.35 | 6.58 | 10.40 | 18.47 | 20000 | 1 |
| \(\theta_7\) | 10.64 | 0.05 | 6.76 | -1.14 | 6.11 | 10.11 | 14.52 | 25.88 | 20000 | 1 |
| \(\theta_8\) | 8.42 | 0.06 | 7.86 | -7.24 | 3.91 | 8.26 | 12.60 | 25.24 | 16598 | 1 |
| lp__ | -39.55 | 0.03 | 2.64 | -45.41 | -41.15 | -39.31 | -37.67 | -35.12 | 6325 | 1 |
表 4.3 的列为后验量的估计值:依次是后验均值 \(\mathsf{E}(\mu|Y)\)、 蒙特卡罗标准误(Monte Carlo standard error)、后验标准差 (standard deviation) \(\mathsf{E}(\sigma|Y)\) 、后验分布的 5 个分位点、有效样本数 \(n_{eff}\) 和潜在尺度缩减因子 (potential scale reduction factor),最后两个量 用来分析采样效率和评估迭代序列的平稳性;最后一行表示每次迭代的未正则的对数后验密度 (unnormalized log-posterior density) \(\hat{R}\),当链条都收敛到同一平稳分布的时候,\(\hat{R}\) 接近 1。
这里对 \(\tau\) 采用的非信息先验是均匀先验,参数 \(\tau\) 的 95% 的置信区间是 \((0.22,20.5)\), 数据支持 \(\tau\) 的范围低于 20.5。
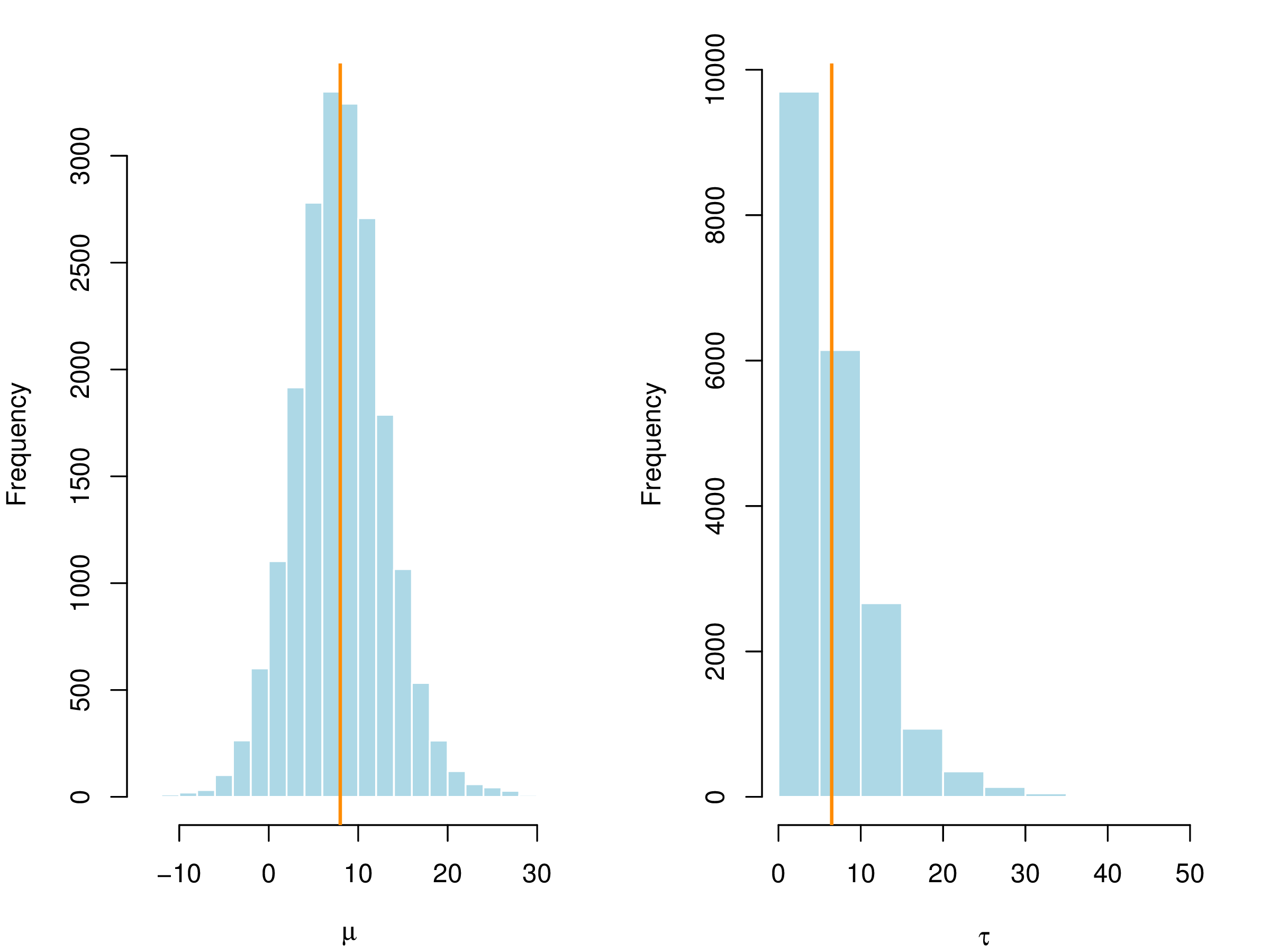
图 4.1: 对 \(\mu,\tau\) 给定均匀先验,后验均值 \(\mu\) 和标准差 \(\tau\) 的直方图


图 4.2: 诊断参数\(\mu,\log(\tau)\)迭代序列的平稳性
为了得到可靠的后验估计,做出合理的推断,诊断序列的平稳性是必不可少的部分,前 5000 次迭代作为 预处理阶段,后 5000 次迭代用作参数的推断,图 4.1 (a) 给出 \(\mu\) 和 \(\log(\tau)\) 的迭代序列图,其中橘黄色线分别是对应的后验均值(表 4.3的第一列),图 4.1 (b) 分别给出 \(\log(\tau)\) 的蒙特卡罗误差,图中显示随着迭代次数增加,蒙特卡罗误差趋于稳定,说明参数 \(\tau\) 的迭代序列达到平稳分布,即迭代点列可以看作来自参数的后验分布的样本。为了评估链条之间和内部的混合效果,Gelman 等 (Gelman et al. 2013) 使用潜在尺度缩减因子 (potential scale reduction factor) \(\hat{R}\) 描述链条的波动程度,类似一组数据的方差含义,方差越小波动性越小,数据越集中,这里意味着链条波动性小。一般地,对于每个待估的量 \(\omega\),模拟产生 \(m\) 条链,每条链有 \(n\) 次迭代值 \(\omega_{ij} (i = 1,\ldots,n;j=1,\ldots,m)\),用 \(B\) 和 \(W\) 分别表示链条之间(不妨看作组间方差)和内部的方差(组内方差)
\[\begin{equation} \begin{aligned} & B = \frac{n}{m-1}\sum_{j=1}^{m}(\bar{\omega}_{.j} - \bar{\omega}_{..} ), \quad \bar{\omega}_{.j} = \frac{1}{n}\sum_{i=1}^{n}\omega_{ij}, \quad \bar{\omega}_{..} = \frac{1}{m}\sum_{j=1}^{m} \bar{\omega}_{.j}\\ & W = \frac{1}{m}\sum_{j=1}^{m}s^{2}_{j}, \quad s^{2}_{j} = \frac{1}{n-1}\sum_{i=1}^{n}(\omega_{ij} - \bar{\omega}_{.j})^2 \end{aligned} \tag{4.32} \end{equation}\]
\(\omega\) 的后验方差 \(\widehat{\mathsf{Var}}^{+}(\omega|Y)\) 是 \(W\) 和 \(B\) 的加权平均
\[\begin{equation} \widehat{\mathsf{Var}}^{+}(\omega|Y) = \frac{n-1}{n} W + \frac{1}{n} B \end{equation}\]
当初始分布发散时,这个量会高估边际后验方差,但在链条平稳或 \(n \to \infty\) 时,它是无偏的。同时,对任意有限的 \(n\),组内方差 \(W\) 应该会低估 \(\mathsf{Var}(\omega|Y)\),因为单个链条没有时间覆盖目标分布;在 \(n \to \infty\), \(W\) 的期望会是 \(\mathsf{Var}(\omega|Y)\)。
通过迭代序列采集的样本估计 \(\hat{R}\) 以检测链条的收敛性
\[\begin{equation} \hat{R} = \sqrt{\frac{\widehat{\mathsf{Var}}^{+}(\omega|Y)}{W}} \end{equation}\]
随着 \(n \to \infty\), \(\hat{R}\) 下降到 1。如果 \(\hat{R}\) 比较大,我们有理由认为需要增加模拟次数以改进待估参数 \(\omega\) 的后验分布。从表 4.3 来看,各参数的 \(\hat{R}\) 值都是 1,说明各个迭代链混合得好。
4.5.4 实现过程
为了与本章第 4.4.3 节提出的贝叶斯 Langevin-Hastings 算法比较,我们基于 Stan 实现求解 SGLMM 模型的贝叶斯汉密尔顿蒙特卡罗算法(简称 Stan-HMC)。目前,我与 Bürkner 一起开发了 brms 包 (Bürkner 2017), 主要工作是修复程序调用和文档书写错误, 特别是与求解 SGLMM 模型相关的 gp 函数,相关细节见 brms 的 Github 开发仓库。
在 SGLMM 模型下,Stan-HMC 算法,先从条件分布 \(S|\boldsymbol{\theta},\boldsymbol{\beta},Y\) 抽样,然后从条件分布 \(\boldsymbol{\theta}|S\) 抽样,最后从条件分布 \(\boldsymbol{\beta}|S,Y\) 抽样,具体步骤如下:
- 选择初始值 \(\boldsymbol{\theta},\boldsymbol{\beta},S\),如 \(\boldsymbol{\beta}\) 的初始值来自正态分布,\(\boldsymbol{\theta}\) 的初始值来自对数正态分布;
- 更新参数向量 \(\boldsymbol{\theta}\) :
- 从指定的先验分布中均匀抽取新的 \(\boldsymbol{\theta}'\) ;
- 以概率 \(\Delta(\boldsymbol{\theta},\boldsymbol{\theta}') = \min \big\{\frac{p(S|\boldsymbol{\theta}')}{p(S|\boldsymbol{\theta})},1\big\}\)接受\(\boldsymbol{\theta}'\),否则不改变 \(\boldsymbol{\theta}\)。
- 更新高斯过程 \(S\) 的取值:
- 抽取新的值 \(S_{i}'\), 向量 \(S\) 的第 \(i\) 值来自一元条件高斯密度 \(p(S_{i}'|S_{-i},\boldsymbol{\theta})\),\(S_{-i}'\) 表示移除 \(S\) 中的第 \(i\) 个值;
- 以概率 \(\Delta(S_{i},S_{i}') = \min\big\{ \frac{p(y_{i}|s_{i}',\boldsymbol{\beta})}{p(y_{i}s_{i},\boldsymbol{\beta})},1 \big\}\) 接受 \(S_{i}'\),否则不改变\(S_i\);
- 重复 (i) 和 (ii) \(\forall i = 1,2,\ldots,n\)。
- 更新模型系数 \(\boldsymbol{\beta}\) :从条件密度 \(p(\boldsymbol{\beta}'|\boldsymbol{\beta})\) 以概率 \[\Delta = \min \big\{ \frac{\prod_{j=1}^{n}p(y_i|s_{i},\boldsymbol{\beta}')p(\boldsymbol{\beta}|\boldsymbol{\beta}')}{\prod_{j=1}^{n}p(y_i|s_{i},\boldsymbol{\beta})p(\boldsymbol{\beta}'|\boldsymbol{\beta})},1 \big\}\] 接受 \(\boldsymbol{\beta}'\),否则不改变\(\boldsymbol{\beta}\);
- 重复步骤2,3,4 既定的次数,获得参数 \(\boldsymbol{\beta},\boldsymbol{\theta}\) 的迭代序列,直到参数的迭代序列平稳,然后根据后续的平稳序列采样,获得各参数后验分布的样本,再根据样本估计参数值。
程序实现的主要步骤(以 R 语言接口 rstan 和 brms 为例说明):首先安装 C++ 编译工具,如果在 Windows 平台上,就从 R 官网下载安装 RTools, 它包含一套完整的 C++ 开发工具。 然后添加 gcc/g++ 编译器的路径到系统环境变量。 如果在 Linux 系统上, 这些工具都是自带的, 环境变量也不用配置, 减少了很多麻烦,但是在 Linux 系统上可以获得更好的算法性能,其它配置细节见 Stan 开发官网。然后,在 R 软件控制台安装 rstan 和 brms 包以及相关依赖包。最后,加载 rstan 和 brms 包,设置启动参数如下:
# 加载程序包
library(rstan)
library(brms)
# 以并行方式运行Stan-HMC算法,指定 CPU 的核心数
options(mc.cores = parallel::detectCores())
# 将编译后的模型写入磁盘,可防止重新编译
rstan_options(auto_write = TRUE)接着调用 brms 包的 brm 函数
fit.binomal <- brm(formula = y | trials(units.m) ~
0 + intercept + x1 + x2 + gp(d1, d2),
data = sim_binom_data,
prior = set_prior("normal(0,10)", class = "b"),
chains = 4, thin = 5, iter = 15000, family = binomial()
) brm 函数可设置的参数有几十个,下面仅列出部分
formula:设置 SGLMM 模型的结构,其中波浪号左侧是响应变量,trials表示在每个采样点抽取的样本量;波浪号右侧0 + intercept表示截距项,x1和x2表示协变量,gp(d1, d2)表示采样坐标为(d1,d2)自相关函数为幂指数族的平稳高斯过程data: SGLMM 模型拟合的数据sim_binom_dataprior: 设置 SGLMM 模型参数的先验分布chains: 指定同时生成马尔科夫链的数目iter: 算法总迭代次数thin:burn-in位置之后,每隔thin的间距就采一个样本family: 指定响应变量服从的分布,如二项分布,泊松分布等
4.6 实现参数估计的 R 包
R 语言作为免费自由的统计计算和绘图环境,因其更新快,社区庞大,扩展包更是超过了 13000 个,提供了大量前沿统计方法的代码实现。如 spBayes 包使用贝叶斯 MCMC 算法估计 SGLMM 模型的参数 (Finley, Banerjee, and E.Gelfand 2015); coda 包诊断马尔科夫链的平稳性 (Plummer et al. 2006);MCMCvis 包分析和可视化贝叶斯 MCMC 算法的输出, 提取模型参数, 转化 JAGS、Stan 和 BUGS 软件的输出结果到 R 对象,以利后续分析;geoR 包 在空间线性混合效应模型上基于 Langevin-Hastings 实现了贝叶斯 MCMC 算法 (Ribeiro Jr. and Diggle 2001);geoRglm 包在 geoR 包的基础上将模型范围扩展到 SGLMM 模型 (Christensen and Ribeiro Jr. 2002);glmmBUGS 包提供了 WinBUGS、 OpenBUGS 和 JAGS 软件的统一接口 (Brown and Zhou 2010)。 目前,R 语言社区提供的求解 SGLMM 模型的 R 包和功能实现,见表 4.4。
| PrevMap | geoR | geoRglm | geostatsp | geoBayes | spBayes | |
|---|---|---|---|---|---|---|
| 二项空间模型 | + | - | + | + | + | + |
| 基于似然函数推断 | + | - | + | - | - | - |
| 基于贝叶斯推断 | + | - | + | + | + | + |
| 模型的块金效应 | + | - | + | + | + | - |
| 低秩近似算法 | + | - | - | - | - | + |
| 分层模型 | + | - | - | + | - | - |
| 非线性预测 | + | +* | + | - | + | + |
| 多元预测 | + | +* | + | - | + | + |
| 空间过程各向异性 | - | +* | + | +* | - | - |
| 非梅隆型协方差函数 | - | +* | + | - | + | + |
参考文献
Alderman, Donald L., and Donald E. Powers. 1980. “The Effects of Special Preparation on Sat-Verbal Scores.” American Educational Research Journal 17 (2): 239–51.
Bolker, Ben, and R Development Core Team. 2017. Bbmle: Tools for General Maximum Likelihood Estimation. https://CRAN.R-project.org/package=bbmle.
Bonat, Wagner Hugo, and Paulo J. Ribeiro Jr. 2016. “Practical Likelihood Analysis for Spatial Generalized Linear Mixed Models.” Environmetrics 27 (2): 83–89.
Brooks, Steve, Andrew Gelman, Galin Jones, and XiaoLi Meng. 2011. Handbook of Markov Chain Monte Carlo. Boca Raton, Florida: Chapman; Hall/CRC.
Brown, Patrick E, and L Zhou. 2010. “MCMC for Generalized Linear Mixed Models with glmmBUGS.” R Journal 2 (1): 13–17.
Bürkner, Paul. 2017. “brms: An R Package for Bayesian Multilevel Models Using Stan.” Journal of Statistical Software 80 (1): 1–28.
Carpenter, Bob, Andrew Gelman, Matthew Hoffman, Daniel Lee, Ben Goodrich, Michael Betancourt, Marcus Brubaker, Jiqiang Guo, Peter Li, and Allen Riddell. 2017. “Stan: A Probabilistic Programming Language.” Journal of Statistical Software 76 (1): 1–32.
Christensen, O. F., and P. J. Ribeiro Jr. 2002. “geoRglm: A Package for Generalised Linear Spatial Models.” R News 2 (2): 26–28.
Christensen, Ole F, Gareth O Roberts, and Martin Sköld. 2006. “Robust Markov Chain Monte Carlo Methods for Spatial Generalized Linear Mixed Models.” Journal of Computational and Graphical Statistics 15 (1): 1–17.
Diggle, Peter J., Patrick Heagerty, Kung-Yee Liang, and Scott L. Zeger. n.d. Analysis of Longitudinal Data. Second. New York: Oxford University Press.
Diggle, Peter J., and Paulo J. Ribeiro Jr. n.d. Model-Based Geostatistics. New York, NY: Springer-Verlag.
Finley, Andrew O., Sudipto Banerjee, and Alan E.Gelfand. 2015. “spBayes for Large Univariate and Multivariate Point-Referenced Spatio-Temporal Data Models.” Journal of Statistical Software 63 (13): 1–28.
Gelman, Andrew, John B. Carlin, Hal S. Stern, David B. Dunson, Aki Vehtari, and Donald B. Rubin. 2013. Bayesian Data Analysis. Third. Boca Raton, Florida: Chapman; Hall/CRC.
Gelman, Andrew, John B. Carlin, Hal S. Stern, and Donald B. Rubin. 2003. Bayesian Data Analysis. Second. London: Chapman; Hall/CRC.
Geyer, Charles J. 1994. “On the Convergence of Monte Carlo Maximum Likelihood Calculations.” Journal of the Royal Statistical Society, Series B 56 (1): 261–74.
Giorgi, Emanuele, and Peter J. Diggle. 2017. “PrevMap: An R Package for Prevalence Mapping.” Journal of Statistical Software 78 (8): 1–29.
Hoffman, Matthew D., and Andrew Gelman. 2014. “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.” Journal of Machine Learning Research 15 (1): 1593–1623.
Kass, Robert E., and Larry Wasserman. 1996. “The Selection of Prior Distributions by Formal Rules.” Journal of the American Statistical Association 91 (435): 1343–70.
Lunn, David, David Spiegelhalter, Andrew Thomas, and Nicky Best. 2009. “The BUGS Project: Evolution, Critique and Future Directions.” Statistics in Medicine 28 (25): 3049–67.
Natarajan, Ranjini, and Charles E. McCulloch. 1995. “A Note on the Existence of the Posterior Distribution for a Class of Mixed Models for Binomial Responses.” Biometrika 82 (3): 639–43.
Plummer, Martyn, Nicky Best, Kate Cowles, and Karen Vines. 2006. “coda: Convergence Diagnosis and Output Analysis for MCMC.” R News 6 (1): 7–11.
Ribeiro Jr., Paulo J., and Peter J. Diggle. 2001. “geoR: A Package for Geostatistical Analysis.” R News 1 (2): 14–18.
Rubin, Donald B. 1981. “Estimation in Parallel Randomized Experiments.” Journal of Educational Statistics 6 (4): 377–401.
Tierney, Luke, and Joseph B. Kadane. 1986. “Accurate Approximations for Posterior Moments and Marginal Densities.” Journal of the American Statistical Association 81 (393): 82–86.
Warnes, J. J., and B. D. Ripley. 1987. “Problems with Likelihood Estimation of Covariance Functions of Spatial Gaussian Processes.” Biometrika 74 (3): 640–42.
黄湘云. 2016. “R 语言做符号计算.” https://cosx.org/2016/07/r-symbol-calculate.
黄湘云. 2017. “随机数生成及其在统计模拟中的应用.” https://cosx.org/2017/05/random-number-generation.
SGLMM 模型的似然函数通常不止一个极值点↩