第 3 章 统计模型
在实际数据分析和建模过程中,模型应该是从简单到复杂以逐步提取数据信息的,并不是直接套用复杂的空间广义线性混合效应模型。就模型的应用来说,如果能用简单模型描述主要的数据特征,那么模型不必往复杂的方向上拓展。但是,在提高少量精度却能带来巨大收益的情况下,模型可以适当增加复杂度。从空间数据建模的角度,我们首先应考虑带空间效应的线性模型和广义线性模型,有时候也叫线性混合效应模型和广义线性混合效应模型,为了突出空间效应,我们把它统一地称作空间线性混合效应模型和空间广义线性混合效应模型。因此,在第 3.1 节,第 3.2 节和第 3.3 节分别回顾了简单线性模型, 广义线性模型和广义线性混合效应模型的结构及其数学表示,并随同模型给出了模型求解的 R 包或函数。第 3.4 节作为重点介绍了空间广义线性混合效应模型(简称 SGLMM),分四个小节介绍模型中的重要成分, 第 3.4.1 小节介绍 SGLMM 模型的各个成分,协变量相关的固定效应和空间位置相关的随机效应,从而引出平稳空间高斯过程,第 3.4.2 小节介绍决定平稳空间高斯过程的关键部分 — 自协方差函数或自相关函数, 第 3.4.3 小节介绍非空间的随机效应,以及它带来的 SGLMM 模型可识别问题与相应处理方式,第3.4.4节介绍文献中使用的先验分布。
3.1 简单线性模型
简单线性模型的一般形式为
\[\begin{equation}
\mathbf{Y} = \mathbf{X}^{\top}\boldsymbol{\beta} + \boldsymbol{\epsilon}, \mathsf{E}(\boldsymbol{\epsilon}) = 0, \mathsf{Cov}(\boldsymbol{\epsilon}) = \sigma^2\mathbf{I} \tag{3.1}
\end{equation}\]
其中,\(\mathbf{Y} = (y_1,y_2,\ldots,y_n)^{\top}\) 是 \(n\) 维列向量,代表对响应变量 \(\mathbf{Y}\) 的 \(n\) 次观测; \(\boldsymbol{\beta} = (\beta_0,\beta_1,\ldots,\beta_{p-1})^{\top}\) 是 \(p\) 维列向量, 代表模型 (3.1) 的协变量 \(\mathbf{X}\) 的系数,\(\beta_0\) 是截距项; \(\mathbf{X}^{\top} = (1_{(1\times n)}^{\top},\mathbf{X}_{(1)}^{\top},\mathbf{X}_{(2)}^{\top},\ldots,\mathbf{X}_{(p-1)}^{\top})\), \(1_{(1\times n)}^{\top}\) 是全 1 的 \(n\) 维列向量,而 \(\mathbf{X}_{(i)}^{\top} = (x_{1i},x_{2i},\ldots,x_{ni})^{\top}\) 代表对第 \(i\) 个自变量的 \(n\) 次观测; \(\boldsymbol{\epsilon} = (\epsilon_1,\epsilon_2,\ldots,\epsilon_n)^{\top}\) 是 \(n\) 维列向量,代表模型的随机误差,并且假定 \(\mathsf{E}(\epsilon_i \epsilon_j) = 0, i \ne j\), 即模型误差项之间线性无关,且方差齐性,都是 \(\sigma^2(>0)\)。 估计模型 (3.1) 的参数常用最小二乘和最大似然方法, 求解线性模型 (3.1) 的参数可以用 R 函数 lm。
3.2 广义线性模型
广义线性模型的一般形式
\[\begin{equation}
g(\mu) = \mathbf{X}^{\top}\boldsymbol{\beta} \tag{3.2}
\end{equation}\]
其中,\(\mu \equiv \mathsf{E}(\mathbf{Y})\), \(g\) 代表联系函数,特别地,当 \(\mathbf{Y} \sim \mathcal{N}(\mu,\sigma^2)\) 时,联系函数 \(g(x) = x\),模型 (3.2) 变为一般线性模型 (3.1)。当 \(\mathbf{Y} \sim \mathrm{Binomial}(n,p)\) 时,响应变量 \(\mathbf{Y}\) 的期望 \(\mu =\mathsf{E}(\mathbf{Y}) = np\), 联系函数 \(g(x)=\ln(\frac{x}{1-x})\),模型 (3.2) 变为\(\log(\frac{p}{1-p})=\mathbf{X}^{\top}\boldsymbol{\beta}\)。 当 \(\mathbf{Y} \sim \mathrm{Poisson}(\lambda)\) 时,响应变量 \(\mathbf{Y}\) 的期望 \(\mu =\mathsf{E}(\mathbf{Y}) = \lambda\), 联系函数\(g(x) = \ln(x)\), 模型 (3.2) 变为 \(\log(\lambda) = \mathbf{X}^{\top}\boldsymbol{\beta}\)。 指数族下其余分布对应的联系函数此处不一一列举, 完整列表可以参看 McCullagh 和 Nelder (1989 年 )(McCullagh and Nelder 1989) 所著的《广义线性模型》 。 模型 (3.2) 最早由 Nelder 和 Wedderburn (1972 年)(Nelder and Wedderburn 1972) 提出,它弥补了模型 (3.1) 的两个重要缺点: 一是因变量只能取连续值的情况, 二是期望与自变量只能用线性关系联系 (陈希孺 2011)。 求解广义线性模型 (3.2) 的 R 函数是 glm, 常用拟似然法去估计模型 (3.2) 的参数。
3.3 广义线性混合效应模型
广义线性混合模型的一般形式 \[\begin{equation} g(\mu) = \mathbf{X}^{\top}\boldsymbol{\beta} + \mathbf{Z}^{\top}\mathbf{b} \tag{3.3} \end{equation}\] 其中, \(\mathbf{Z}^{\top}\) 是 \(q\) 维随机效应 \(\mathbf{b}\) 的 \(n \times q\) 的数据矩阵,其它符号含义如前所述。广义线性混合效应模型中既包含固定效应 \(\boldsymbol{\beta}\) 又包含随机效应 \(\mathbf{b}\) 。 线性模型 (3.1) 和广义线性模型 (3.2) 中的协变量都是固定效应, 而随机效应是那些不能直接观察到的潜效应, 但是对响应变量却产生显著影响。 特别是在基因变异位点与表现型的关系研究中, 除了用最新科技做全基因组扫描获取显著的基因位点, 还应该把那些看似不显著, 联合在一起却显著的位点作为随机效应去考虑 (Yang et al. 2010)。求解模型 (3.3)的 R 包有 nlme ,mgcv 和 lme4, 参数估计的方法有限制极大似然法。 除了求解模型 (3.3) 外, nlme 还可以拟合一些非线性混合效应模型, mgcv 可以拟合广义可加混合效应模型, lme4 使用了高性能的 Eigen 数值代数库,可以加快模型的求解进程。
3.4 空间广义线性混合效应模型
3.4.1 模型结构
空间广义线性混合效应模型是对模型 (3.3) 的进一步延伸,其一般形式为 \[\begin{equation} g(\mu_i) = d(x_i)^{\top}\boldsymbol{\beta} + S(x_i) + Z_i \tag{3.4} \end{equation}\] 其中,\(d^{\top}(x_i)\) 表示协变量对应的观测数据向量,即 \(p\) 个协变量在第 \(i\) 个位置 \(x_i\) 的观察值。 这里, 假定 \(\mathcal{S} = \{S(x): x \in \mathbb{R}^2\}\) 是均值为\(\mathbf{0}\), 方差为 \(\sigma^2\),平稳且各向同性的空间高斯过程, \(\rho(x,x') = \mathsf{Corr}\{S(x),S(x')\} \equiv \rho(\|x,x'\|)\), \(\|\cdot\|\) 表示距离。 样本之间的位置间隔不大就用欧氏距离, 间隔很大可以考虑用球面距离; \(S(x_i)\) 代表了与空间位置 \(x_i\) 相关的随机效应, 简称空间效应。 \(Z_i \stackrel{i.i.d}{\sim} \mathcal{N}(0,\tau^2)\) 的非空间随机效应, 也称块金效应, 一般解释为测量误差 (measurement error) 或微观变化 (micro-scale variation) (Christensen 2004), 即 \(\tau^2=\mathsf{Var}(Y_{i}|S(x_{i})),\forall i = 1,2, \ldots, N\), \(N\) 是采样点的数目, 其它符号含义不变。
3.4.2 自协方差函数
模型 (3.4) 的空间效应结构设定为随机过程 \(\mathcal{S} = \{S(x): x \in \mathbb{R}^2\}\),它由自协方差函数决定。在给出随机过程 \(\mathcal{S}\) 的自协方差函数之前, 先计算一下它的理论变差 \(V(x,x')\) 和模型 (3.4) 中 \(T_{i}\) 的变差 \(V_{T}(u_{ij})\)1。为方便起见,记 \(T_{i} = d(x_i)^{\top}\boldsymbol{\beta} + S(x_i) + Z_i\) \[\begin{equation} \begin{aligned} V(x,x') &= \frac{1}{2}\mathsf{Var}\{S(x)-S(x')\}\\ &= \frac{1}{2}\mathsf{Cov}(S(x)-S(x'),S(x)-S(x'))\\ &= \frac{1}{2}\{\mathsf{E}[S(x)-S(x')][S(x)-S(x')]-[\mathsf{E}(S(x)-S(x'))]^2\}\\ &= \sigma^2-\mathsf{Cov}(S(x),S(x'))=\sigma^2\{1-\rho(u)\}\\ V_{T}(u_{ij}) &= \frac{1}{2}\mathsf{Var}\{T_{i}(x)-T_{j}(x)\} \\ &= \frac{1}{2}\mathsf{E}[(T_{i}-T_{j})^2]=\tau^2+\sigma^2(1-\rho(u_{ij})) \end{aligned} \tag{3.5} \end{equation}\] 从方程 (3.5) 不难看出系数 \(\frac{1}{2}\) 的化简作用,类似地,根据协方差定义可推知随机向量 \(T = (T_1,T_2,\ldots,T_n)\) 的协方差矩阵结构如下: \[\begin{equation} \begin{aligned} \mathsf{Cov}(T_{i}(x),T_{i}(x)) &= \mathsf{E}[S(x_i)]^2 + \mathsf{E}Z_{i}^{2}= \sigma^2+\tau^2 \\ \mathsf{Cov}(T_{i}(x),T_{j}(x)) &= \mathsf{E}[S(x_i)S(x_j)] = \sigma^2\rho(u_{ij}) \end{aligned} \end{equation}\] 自相关函数 \(\rho(u)\) 的作用和地位就显而易见了,它是既决定理论变差又决定协方差矩阵的结构。图 3.1 给出一般变差函数的示意图,作为粗略估计,纵截距可以看作是块金效应参数 \(\tau^2\),而图中的变差函数基台值,即变差函数 \(V_{T}(u_{ij})\) 趋于稳定的函数值,它是块金效应和空间效应的和,作为空间效应参数 \(\sigma^2\) 的粗略估计,我们用基台值减去块金效应即得。基于样本变差函数图 3.1 我们可以获得随机效应方差分量的初始估计,其使用案列见第 6 章第 6.1 节。
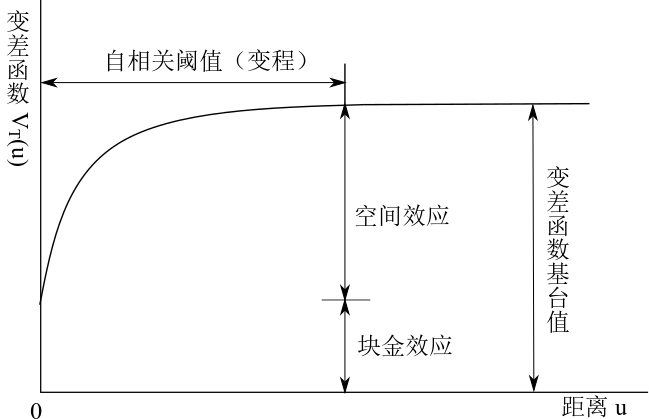
图 3.1: 变差函数 \(V_{T}(u)\) 示意图
常见的自相关函数有三类,分别是高斯型自相关函数、球面型自相关函数和 Matérn 型自相关函数,由于 Matérn 型自相关函数的广泛应用性 (Diggle, Tawn, and Moyeed 1998; Diggle et al. 2002; Christensen 2004),这里主要介绍它的有关性质特点。 \[\begin{equation} \rho(u)=\{2^{\kappa -1}\Gamma(\kappa)\}^{-1}(u/\phi)^{\kappa}\mathcal{K}_{\kappa}(u/\phi),u > 0 \tag{3.6} \end{equation}\] 一般地,假定 \(\rho(u)\) 单调不增,即任何两样本之间的相关性应该随距离变大而减弱,尺度参数 \(\phi\) 控制函数 \(\rho(u)\) 递减到0的速率。方便起见,记 \(\rho(u) = \rho_{0}(u/\phi)\),则方程 (3.6) 可简记为 \[\begin{equation} \rho_{0}(u)=\{2^{\kappa -1}\Gamma(\kappa)\}^{-1}(u)^{\kappa}\mathcal{K}_{\kappa}(u),u > 0 \tag{3.7} \end{equation}\] 其中,\(\mathcal{K}_{\kappa}(\cdot)\) 是阶数为 \(\kappa\) 的第二类修正的贝塞尔函数,函数图像见图 3.2, \(\kappa(>0)\) 是平滑参数,满足这些条件的空间过程 \(\mathcal{S}\) 是 \(\lceil\kappa\rceil-1\) 次均方可微的。值得注意的是 Matérn 型包含幂指数型 当 \(\kappa = 0.5\)时,\(\rho_{0}(u) = \exp(-u)\), \(S(x)\) 均方连续但是不可微,当 \(\kappa \to \infty\) 时, \(\rho_{0}(u) = \exp(-u^2)\), \(S(x)\) 无限次均方可微(Peter J. Diggle and Ribeiro Jr., n.d.)。
下面详细给出修正的第二类贝塞尔函数 \(\mathcal{K}_{\kappa}(u)\),它是修正的贝塞尔方程的解 (Abramowitz and Stegun 1972),函数形式如下
\[\begin{equation} \begin{aligned} I_{-\kappa}(u) & = \sum_{m=0}^{\infty} \frac{1}{m!\Gamma(m + \kappa + 1)} \big(\frac{u}{2}\big)^{2m + \kappa} \\ \mathcal{K}_{\kappa}(u) & = \frac{\pi}{2} \frac{I_{-\kappa}(u) - I_{\kappa}(u)}{\sin (\kappa \pi)} \end{aligned} \tag{3.8} \end{equation}\]
其中 \(u \geq 0\),\(\kappa \in \mathbb{R}\),如果 \(\kappa \in \mathbb{Z}\),则取该点的极限值,\(\mathcal{K}_{\kappa}(u)\) 的值可由 R 内置的函数 besselK 计算。
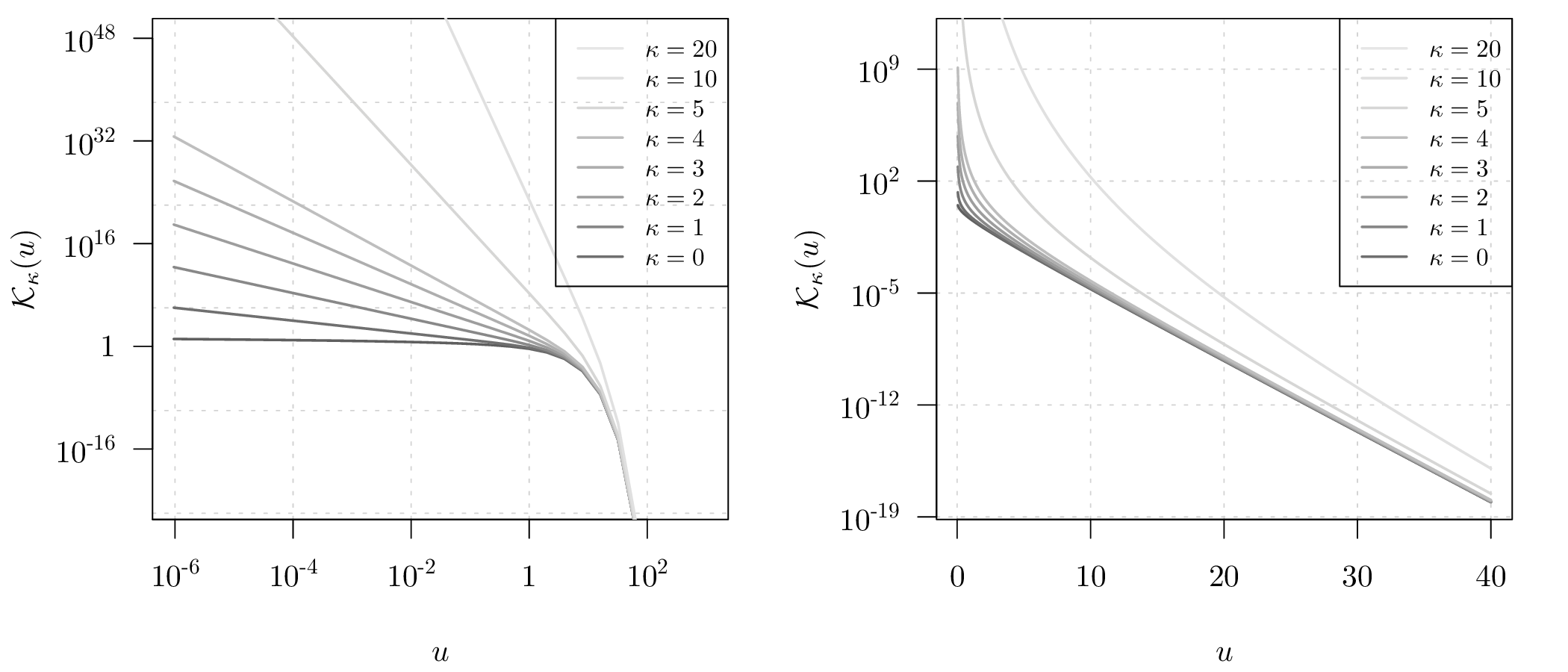
图 3.2: 修正的第二类贝塞尔函数图像
在实际数据分析中,估计 \(\kappa\) 时,为了节省计算,又不失一般性,经验做法是取离散的 \(\kappa\) 值,如 \(\kappa = 0.5, 1.5, 2.5\), 这样,平稳空间高斯过程就分别具有均方连续不可微、一次可微和二次可微三种不同程度的光滑性。根据第 2 章第 2.4 节定理 2.4,自相关函数 \(\rho(u)\) 的可微性表示了空间过程 \(\mathcal{S}\) 的曲面平滑程度。为更加直观地观察 \(\rho(u)\),作图 3.3 和图 3.4。
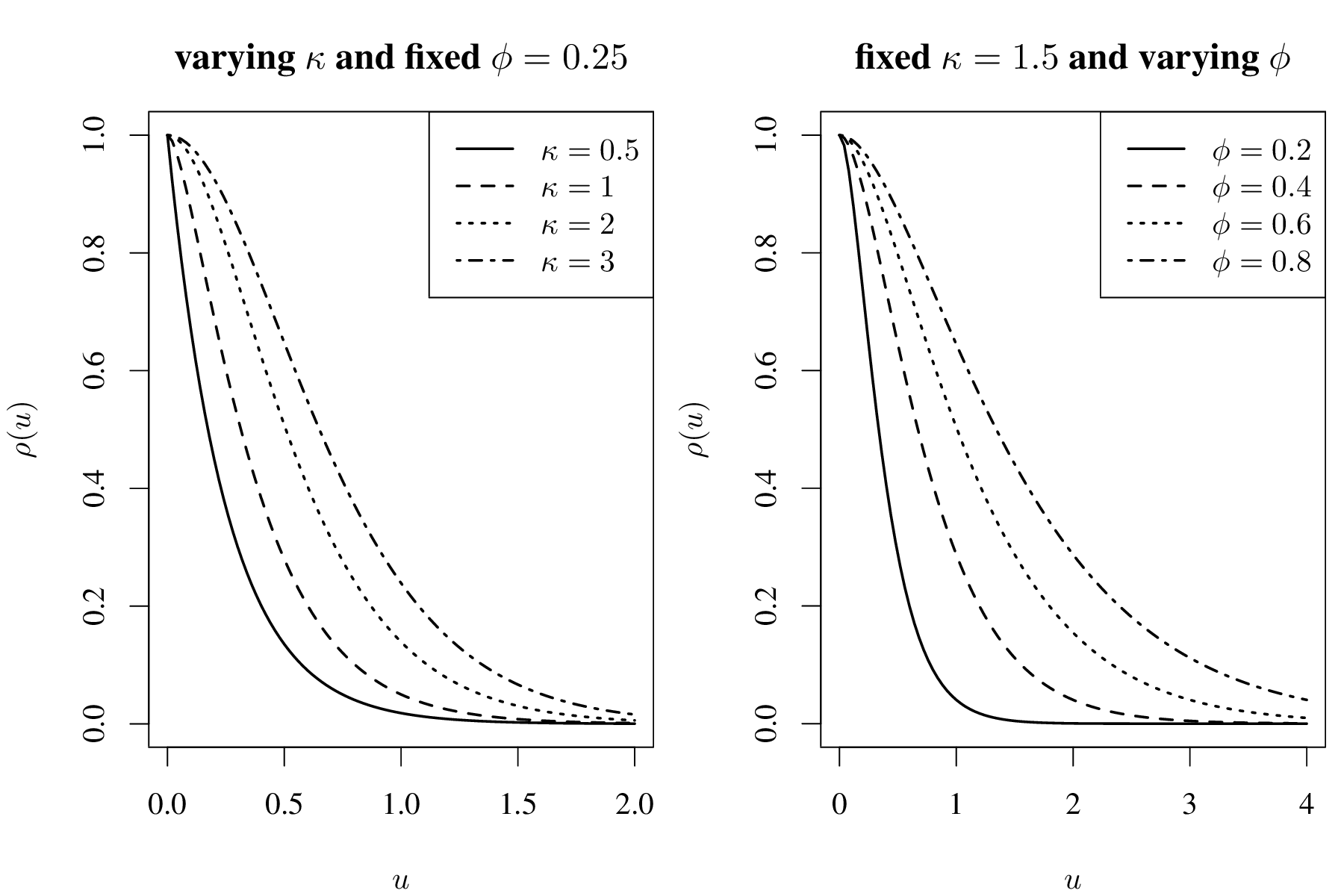
图 3.3: 自相关函数 \(\rho(u)\) 随尺度参数 \(\phi\)(左图)和平滑参数 \(\kappa\) (右图)的变化
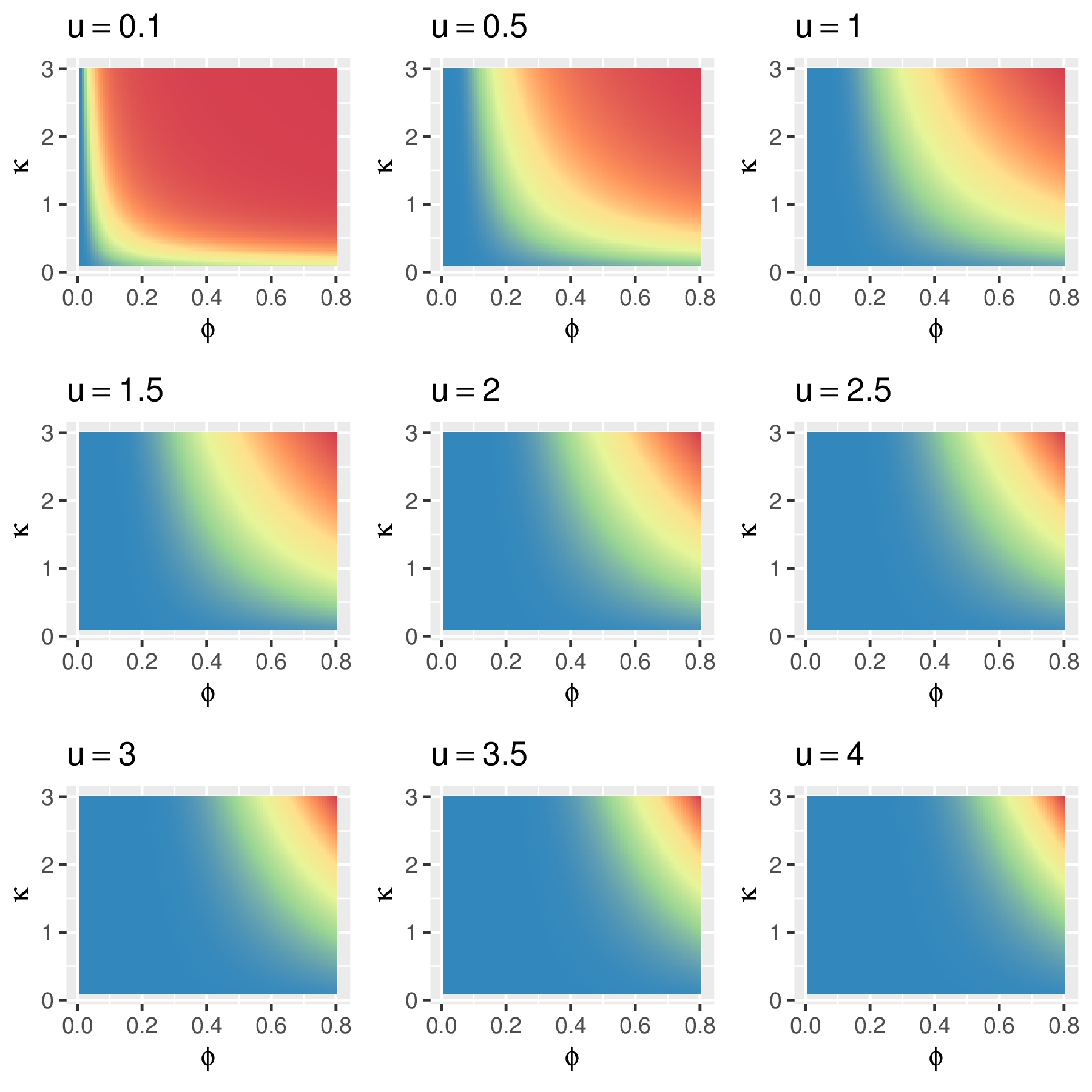
图 3.4: \(\rho(\mathsf{u})\) 在不同空间距离 \(\mathsf{u}\)处随 \(\kappa\) 和 \(\phi\) 的变化,从蓝到红的颜色变化表示 \(\rho(\mathsf{u})\) 的值由小到大
从图3.3可以看出,相比于贝塞尔函数的阶 \(\kappa\), 尺度参数 \(\phi\) 对相关函数的影响大些,由图3.3看出随着空间距离的增加,相关性减弱地特别快。在实际应用中,先固定下 \(\kappa\) 是可以接受的,为简化编程和表述,Diggle 等 (1998年) (Diggle, Tawn, and Moyeed 1998) 在真实数据分析中使用幂指数型自相关函数 \(\rho_{0}(u) = \exp(-(\alpha u)^{\delta}), \alpha > 0, 0 < \delta \leq 2\)。 虽然其形式大大简化, 但函数图像和性质却与Matérn 型有相似之处, 即当 \(0 < \delta < 2\) 时, \(S(x)\) 均方连续但不可微,当 \(\delta = 2\) 时, \(S(x)\) 无限次可微。
3.4.3 模型识别
在 SGLMM 模型的实际应用当中,一般先不添加非空间的随机效应,而是基于模型 (3.9) 估计参数,估计完参数,代入模型,观察线性预测 \(\hat{T_{i}}\) 和真实的 \(T_i\) 之间的残差,如残差表现不平稳,说明还有非空间的随机效应没有提取,因此添加块金效应是合理的,此时在模型 (3.4) 中有两个来源不同的随机效应 \(Z_{i}\) 与 \(S(x_i)\)。 \[\begin{equation} g(\mu_i) = d(x_i)^{\top}\boldsymbol{\beta} + S(x_i) \tag{3.9} \end{equation}\] 如何区分开 \(Z_{i}\) 与 \(S(x_i)\),或者更直接地说,如何估计这两个随机效应的参数 \(\tau^2, \sigma^2, \phi\), 即为可识别问题。 向量 \(T = (T_1,T_2,\ldots,T_n)^{\top}\) 是协方差矩阵为 \(\tau^2I + \sigma^2R\) 的多元高斯分布, 其中, 自相关函数 \(R_{ij} = \rho(u_{ij}; \phi)\), \(u_{ij}\) 是 \(x_i\) 与 \(x_j\) 之间的距离。由线性预测 \(T_{i}\) 的变差公式 (3.5) 知,随机过程 \(T(x)\) 的变差 \(\tau^2 + \sigma^2(1-\rho(u_{ij}))\) 和自相关函数 (3.10) \[\begin{equation} \rho^{\star}(u) = \begin{cases} 1 & : x_{i} = x_{j} \\ \sigma^2\rho(u_{ij})/(\sigma^2+\tau^2) & : x_{i} \neq x_{j} \end{cases} \tag{3.10} \end{equation}\] 在原点不连续,只有当 \(\tau^2 = \mathsf{Var}[Y_i|S(x_i)]\) 已知或者在同一位置可以用重复测量的方法直接获得时,参数 \(\tau^2, \sigma^2, \phi\) 是可识别的 (Diggle et al. 2002; Peter J. Diggle and Ribeiro Jr., n.d.)。如果通过探索性数据分析观察到不可忽略的非空间效应 \(\tau^2\) 时,Christensen (2004年) (Christensen 2004) 建议使用样本变差函数对 \(\tau^2\) 作初步估计,然后计算关于 \(\tau^2\) 的剖面似然函数曲线,或者协方差参数 \(\phi,\tau^2\)一起确定最佳的值,第 6 章第 6.2 节将用剖面似然函数曲面的方法获取真实数据场景中的参数估计值。
3.4.4 先验分布
基于贝叶斯方法实现模型 (3.4) 的参数估计,必然使用 MCMC 算法,自然地,需要指定模型参数 \(\boldsymbol{\theta} = (\boldsymbol{\beta},\tau^2,\sigma^2,\phi)\) 的先验分布。对于 \(\boldsymbol{\beta}\),Diggle 等 (2002 年) (Diggle et al. 2002) 选择相互独立的均匀先验,而对于参数 \(\tau^2,\sigma^2,\phi\),选取如下模糊先验: \[f(\tau^2) \propto \frac{1}{\tau^2};f(\sigma^2) \propto \frac{1}{\sigma^2};f(\phi) \propto \frac{1}{\phi^2}\] 其中,\(\tau^2\) 和 \(\sigma^2\) 为 Jeffreys 先验,Diggle 等 (2002 年) (Diggle et al. 2002) 使用如下先验分布 \[\begin{equation*} \log(\nu^2),\log(\sigma^2),\log(\phi) \sim \mathcal{N}(\cdot,\cdot) \end{equation*}\] 这些无信息先验分布的选择主要是出于实用和经验的考虑,也可以取别的,只要保持马尔科夫链收敛即可。实际操作中,我们还选取不同初始值,产生多条链,同时去掉迭代初始阶段产生的相对发散的参数迭代值,后续迭代值在链条收敛的情况下,可以把它当作后验分布产生的样本,然后依据该样本估计后验分布的参数。
参考文献
Abramowitz, Milton, and Irene A. Stegun. 1972. Handbook of Mathematical Functions. Tenth. New York: National Bureau of Standards.
Christensen, Ole F. 2004. “Monte Carlo Maximum Likelihood in Model-Based Geostatistics.” Journal of Computational and Graphical Statistics 13 (3): 702–18.
Diggle, Peter J., Rana Moyeed, Barry Rowlingson, and Madeleine Thomson. 2002. “Childhood Malaria in the Gambia: A Case-Study in Model-Based Geostatistics.” Journal of the Royal Statistical Society, Series C 51 (4): 493–506.
Diggle, Peter J., and Paulo J. Ribeiro Jr. n.d. Model-Based Geostatistics. New York, NY: Springer-Verlag.
Diggle, Peter J., J. A. Tawn, and R. A. Moyeed. 1998. “Model-Based Geostatistics.” Journal of the Royal Statistical Society, Series C 47 (3): 299–350.
McCullagh, Peter, and John Nelder. 1989. Generalized Linear Models. Second. London: Chapman; Hall/CRC.
Nelder, John A., and R. W. M. Wedderburn. 1972. “Generalized Linear Models.” Journal of the Royal Statistical Society, Series A 135 (3): 370–84.
Yang, Jian, Beben Benyamin, Brian P Mcevoy, Scott Gordon, Anjali K Henders, Dale R Nyholt, Pamela A Madden, Andrew C Heath, Nicholas G Martin, and Grant W Montgomery. 2010. “Common Snps Explain a Large Proportion of Heritability for Human Height.” Nature Genetics 42 (7): 565–69.
陈希孺. 2011. 广义线性模型的拟似然法. 合肥: 中国科学技术大学出版社.