4 R’da Build-in Fonksiyonlar Yardımıyla Basit Doğrusal Regresyon

R’da bulunan hazır fonksiyonları gördükten sonra yukarıda yapılan işlemleri gereksiz görebilirsiniz. Evet, herhangi bir regresyon modeli oluştururken yukarıdaki işlemlerin hiçbirini yapmanıza, bu hazır fonksiyonlar sayesinde gerek yok. Kodları açık açık yazmanın öğrenmek için daha iyi bir yol olduğunu düşündüğüm için, önceki bölümün kodlarını yazma gereksinimi hissettim. Ancak isteyen kişiler doğrudan buradan da devam edebilirler.

4.1 Modelin Kuruluşu

lm() fonksiyonu(lineer model) ile doğrusal regresyon modeli kurulabilir.

model <- lm(sales ~ TV , data = df1)
# lm(bağımlı değişken  ~ bağımsız değişken, data = veri)
model
## 
## Call:
## lm(formula = sales ~ TV, data = df1)
## 
## Coefficients:
## (Intercept)           TV  
##     7.03259      0.04754

Görüldüğü üzere kolayca katsayıları elde ettik.

Modelimizi daha detaylı incelemek için;

summary(model)
## 
## Call:
## lm(formula = sales ~ TV, data = df1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -8.3860 -1.9545 -0.1913  2.0671  7.2124 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.032594   0.457843   15.36   <2e-16 ***
## TV          0.047537   0.002691   17.67   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 3.259 on 198 degrees of freedom
## Multiple R-squared:  0.6119, Adjusted R-squared:  0.6099 
## F-statistic: 312.1 on 1 and 198 DF,  p-value: < 2.2e-16

  • Residuals kısmında artıkların istatistiksel bazı özellikleri görülmektedir.

  • Coefficients: Kısmında katsayılarla ilgili bilgiler bulunmaktadır.

    • \(\hat{\beta}_{0}\) tahmin değeri 7.03 , standart sapması 0.457, t istatistiği 15.36 olarak verilmiştir.
    • \(\hat{\beta}_{1}\) tahmin değeri 0.047 , standart sapması 0.002691, t istatistiği 17.67 olarak verilmiştir.
    • Signif. codes: kısmında anlamlılık düzeyleri verilmiştir. 0.001 anlamlılık düzeyinde üç yıldız, 0.01 anlamlılık düzeyinde 2, 0.05’de tek yıldızdır.Katsayılarımızın yanında 3 yıldız olduğu için 0.001 anlamlılık düzeyinde anlamlıdır diyebiliriz.

  • Resdiual standard error kısmında artıklarımızın RSE değeri 3.259 verilmiştir.

  • Multiple R-squared ile \(R^{2}\) değeri 0.6119 verilmiştir.

  • F-statistic ve p-value değerleri modelin genel olarak anlamlılığını sorgulamamızı sağlar. F-statistic değeri 312.1 verilmiştir. 312.1 çok yüksek bir F değeri olduğundan modelimiz anlamlıdır diyebiliriz. p-value değeri modelimizin genel olarak anlamlılığını sınar, 0 hipotezi modelin anlamsız olduğudur. p-value değeri 0.05 den küçük olduğunda (p-value<0.05) 0 hipotezi reddedilir. Yani modelimiz anlamlıdır.

4.2 Katsayılar İçin Güven Aralığı

confint(model)
##                  2.5 %     97.5 %
## (Intercept) 6.12971927 7.93546783
## TV          0.04223072 0.05284256

4.3 ANOVA

anova(model)
## Analysis of Variance Table
## 
## Response: sales
##            Df Sum Sq Mean Sq F value    Pr(>F)    
## TV          1 3314.6  3314.6  312.14 < 2.2e-16 ***
## Residuals 198 2102.5    10.6                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  • Burada Mean Sq sütununda artıkların varyansını(\(MSE\)) 10.6 görebiliriz. Bu aynı zamanda modelimizin de varyansıdır.
  • Yukarıdaki model özetinde olduğu gibi burada da F İstatistiği ve p-value değeri hesaplanmıştır. Yorumları aynı şekildedir. Modelimiz 0.001 anlamlılık düzeyinde anlamlıdır.

4.4 Modeli Görselleştirme

modelSummary <- summary(model)
# model katsayıları
modelCoeffs <- modelSummary$coefficients  
modelCoeffs
##               Estimate  Std. Error  t value    Pr(>|t|)
## (Intercept) 7.03259355 0.457842940 15.36028 1.40630e-35
## TV          0.04753664 0.002690607 17.66763 1.46739e-42
# beta1 şapka değerini almak için.
beta1_tahmin <- modelCoeffs["TV", "Estimate"]
beta0_tahmin <- modelCoeffs[1, "Estimate"]
beta1_tahmin; beta0_tahmin
## [1] 0.04753664
## [1] 7.032594
library("ggplot2")
denklem <-  paste0("y = ", round(beta0_tahmin,4), " + ",round(beta1_tahmin,4), "*x ")
# Plot
grafik1 <- ggplot(data=df1, aes(x=x, y=y)) + geom_point(col="blue")
grafik1 + geom_abline(intercept = beta0_tahmin, slope =beta1_tahmin,size=1,col="red")+
  ggtitle(denklem)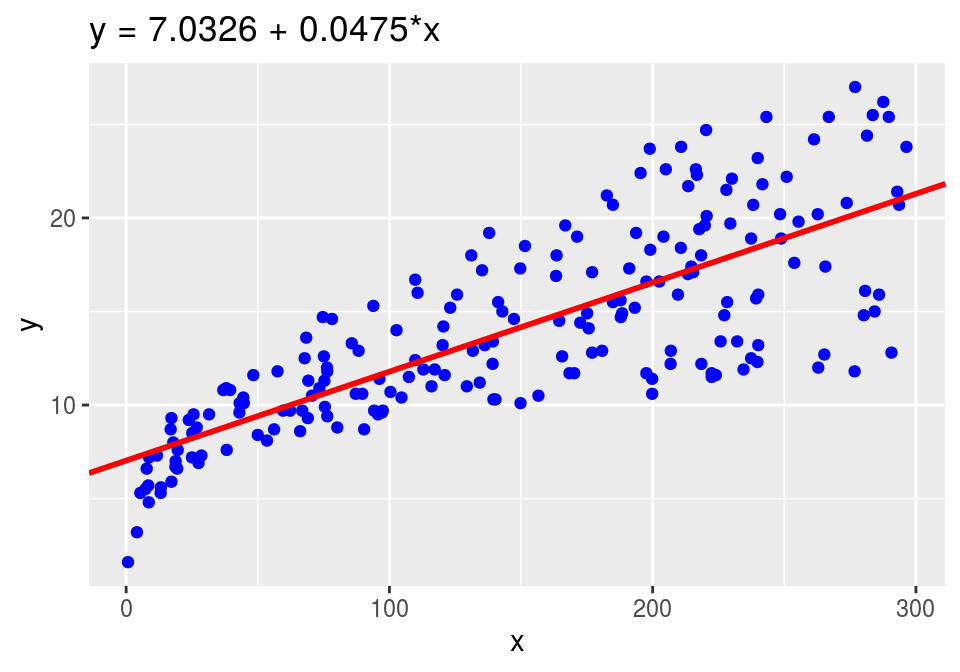
Fit Edilmiş Regresyon Doğrusu

Şekil 4.1: Fit Edilmiş Regresyon Doğrusu