Doğrusal (Lineer) Regresyon
1 Giriş
Lineer (Doğrusal) regresyon istatistiksel veri analizinde sıkça kullanılan bir yöntemdir. Lineer regresyon, doğrusal ve sürekli değişkenler için kullanılan bir yöntemdir. Son yıllarda popüler olan makine öğrenmesi açısından ise birçok kaynakta giriş konusudur. Dolayısıyla bu konunun iyi kavranması makine öğrenmesi konusunda kendisini geliştirmek isteyenler için elzemdir.
Bu dökümanda doğrusal regresyonun teorik kısımlarından çok, R ile uygulama kısımları yer alacaktır. Aşağıda doğrusal regresyon modelini iki örnek ile nerede ve nasıl kullanabileceğimizi anlatmaya çalıştım.
Wikipedia’nın “ileri demokrasi” filtremizden geçmesi şerefine: Örneğin, bir ziraat mühendisi buğday verimi ve gübre miktarı arasındaki ilişkiyi, bir mühendis, basınç ve sıcaklık, bir ekonomist gelir düzeyi ve tüketim harcamaları, bir eğitimci öğrencilerin devamsızlık gösterdiği gün sayıları ve başarı dereceleri arasındaki ilişkiyi bilmek isteyebilir. Regresyon, iki (ya da daha çok) değişken arasındaki doğrusal ilişkinin fonksiyonel şeklini, biri bağımlı diğeri bağımsız değişken olarak bir doğru denklemi olarak göstermekle kalmaz, değişkenlerden birinin değeri bilindiğinde diğeri hakkında kestirim yapılmasını sağlar. Genellikle bu iki (veya çok) değişkenlerin hepsinin niceliksel ölçekli olması zorunluluğu vardır.
Konuyu daha iyi kavramak için bazı örnekler incelenebilir. Örneğin metre ve inch uzunluk ölçüsü birimlerini kıyaslamak istedik;
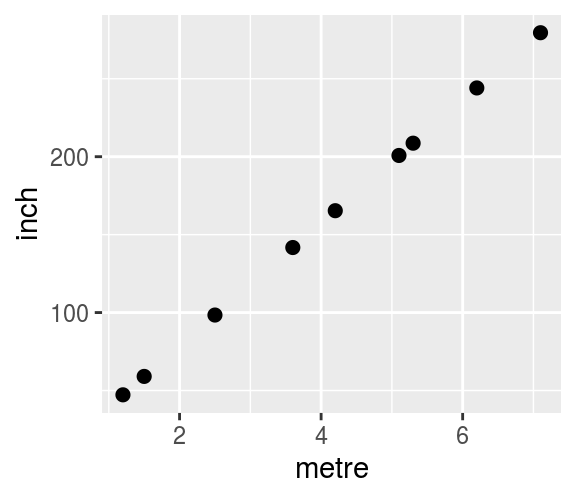
Şekil 1.1: inch ~ metre
Şekil 1.1’de tam bir doğrusallık söz konusudur. inch = metre * 39.70 eşitliği geçerlidir, yani 10 metrenin 393.70 inch geleceğini yukarıdaki formül ile hesaplayabiliriz. Günlük hayatta değişkenler arasında, birimler gibi tam doğrusal ilişkiler gözlemlenemez. Genelde bir rassallık söz konusudur. Değişkenler arasında doğrusal ilişki gözlendiğinde geleceğe dair tahminde bulunmak, değişkenlerin birbirleri üzerinde nasıl etkide bulunduğunu incelemek ve çıkarım yapmak için doğrusal regresyon modeli kullanılır. Bu model, yukarıdaki modelle benzerdir, basit doğrusal regresyon modelinde y eksenini kesim noktası, doğrunun eğimi ve sonunda ise \(\epsilon\)(hata terimi) vardır. Tek bir bağımsız değiken olduğunda regresyon modeline Basit Doğrusal Regresyon, birden fazla bağımsız değişken olduğunda ise Çoklu Doğrusal Regresyon Modeli denir.
Başka bir örnek olarak, Eskişehir’de yaşayan 30 öğrencinin aylık gelirleri ile giderlerinin verisine ulaşılır ve gelir ve giderleri serpilme diyagramıyla aşağıdaki gibi çizdirilirse;
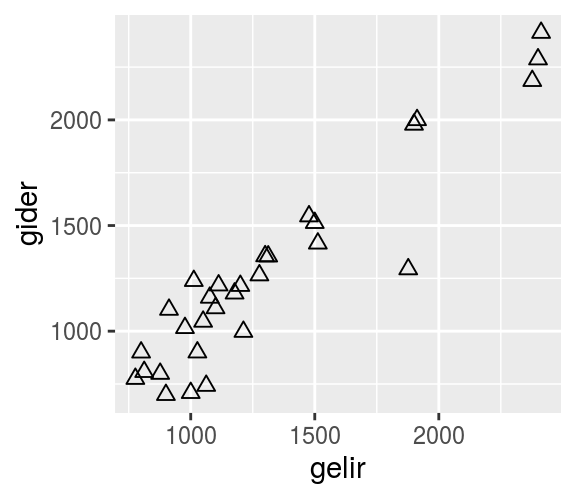
Şekil 1.2: Gelir - Gider Grafiği
Şekil 1.2’de görüleceği gibi öğrencilerin gelir ve giderleri arasında doğrusal bir ilişki bulunmaktadır. Ancak tam bir doğrusallık yoktur, belli bir rassallık vardır. Herhangi bir öğrencinin gelirini bildiğimizde, kesin olarak giderini söyleyemeyiz. Ancak elimizdeki veriyi doğrusal regresyon ile modellersek belki küçük bir hata ile gelirini bildiğimiz bir öğrencinin giderini tahmin edebiliriz.
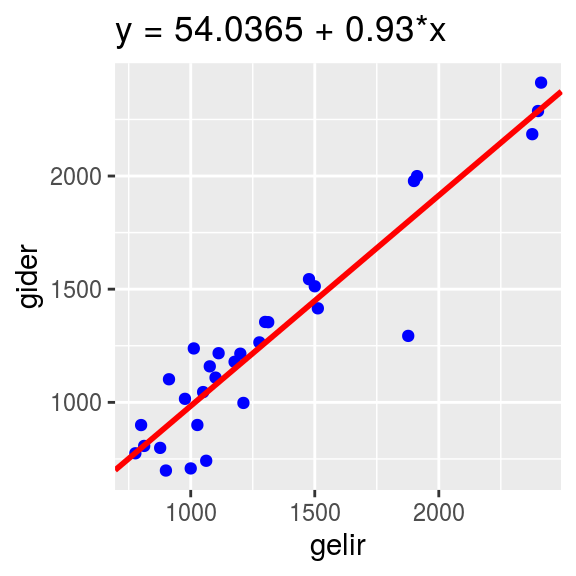
Şekil 1.3: Fit Edilmiş Gelir Gider Grafiği
Regresyon modeli, Şekil 1.3’ün üzerinde bulunan fonksiyon şeklinde kurulabilir.. Eğer aylık 2000 lira geliri olan bir öğrencinin giderini tahmin edersek 1829.423 lira olarak buluruz. Bu bizim tahmin değerimizdir, bu öğrencinin aylık gideri 1800 lira olabilir, 2200 lira da olabilir. Ancak geliri 2000 lira olan 1000 tane öğrencinin giderlerinin ortalamasına bakarsak 1829.423 değerine yakın olacaktır. Bu fonksiyon(model) sayesinde herahangi bir öğrencinin X lira geliri olduğunu bildiğimizde ortalama Y(kaç) lira gideri olacağını tahmin edebiliriz. Kısacası doğrusal regresyon modeli ile ortalama, beklenti buluruz.