3 R ile Basit Doğrusal Regresyon Uygulaması
Uzun uzun işlem yapmak istemeyen, sadece sonucu görmek isteyenler, aşağıdaki R’da Build-in Fonksiyonlar Yardımıyla Basit Doğrusal Regresyon kısmına geçebilir.
3.0.1 Veri Setine Genel Bakış
3.0.1.1 Veri setinin import edilmesi.
## Classes 'tbl_df', 'tbl' and 'data.frame': 200 obs. of 4 variables:
## $ TV : num 230.1 44.5 17.2 151.5 180.8 ...
## $ radio : num 37.8 39.3 45.9 41.3 10.8 48.9 32.8 19.6 2.1 2.6 ...
## $ newspaper: num 69.2 45.1 69.3 58.5 58.4 75 23.5 11.6 1 21.2 ...
## $ sales : num 22.1 10.4 9.3 18.5 12.9 7.2 11.8 13.2 4.8 10.6 ...## TV radio newspaper sales
## Min. : 0.70 Min. : 0.000 Min. : 0.30 Min. : 1.60
## 1st Qu.: 74.38 1st Qu.: 9.975 1st Qu.: 12.75 1st Qu.:10.38
## Median :149.75 Median :22.900 Median : 25.75 Median :12.90
## Mean :147.04 Mean :23.264 Mean : 30.55 Mean :14.02
## 3rd Qu.:218.82 3rd Qu.:36.525 3rd Qu.: 45.10 3rd Qu.:17.40
## Max. :296.40 Max. :49.600 Max. :114.00 Max. :27.003.0.2 Korelasyon Matrisi
Değişkenlerin birbirleri üzerindeki etkisini incelemek için korelasyon matrisi kullanılabilir.
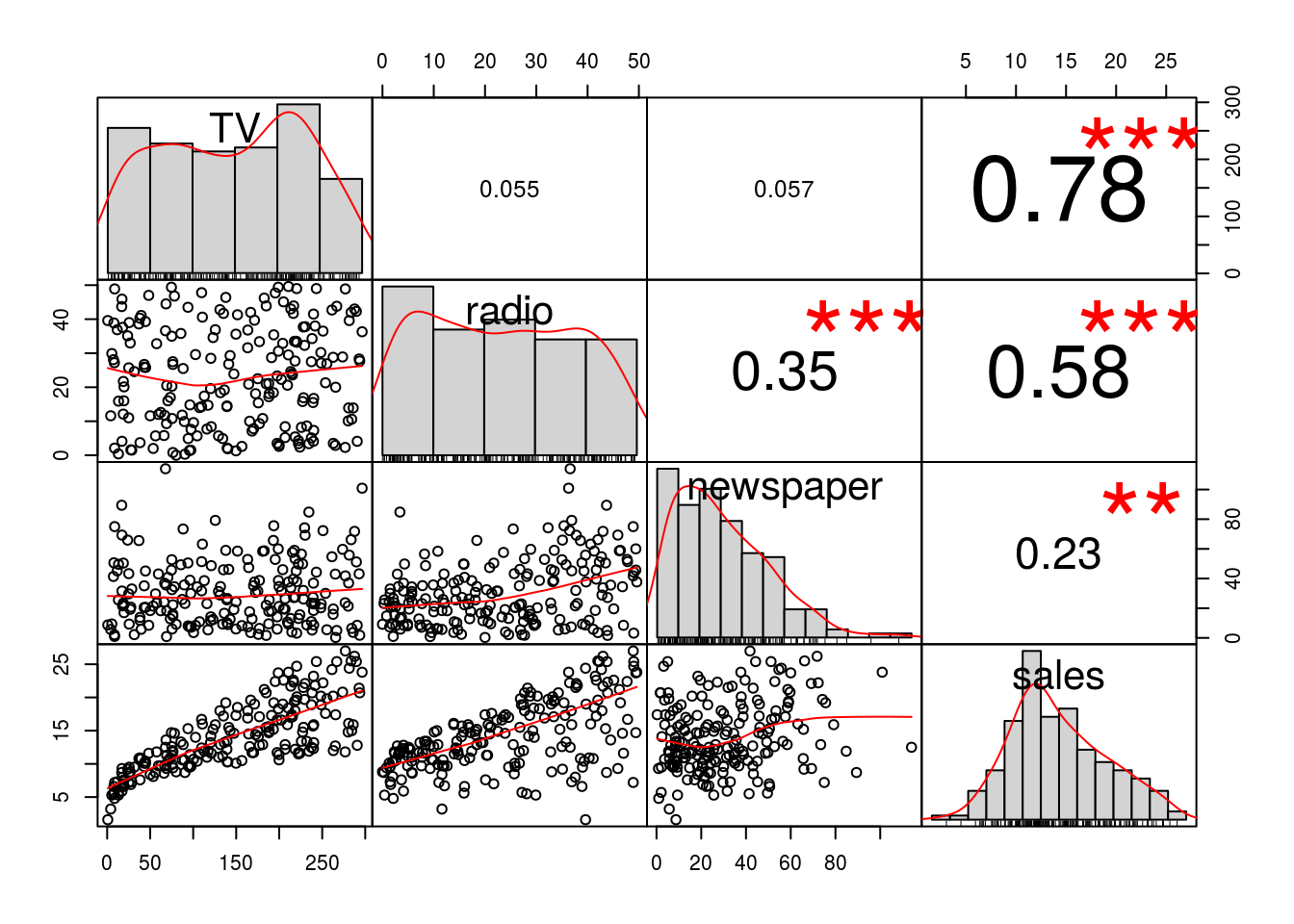
Şekil 3.1: Tüm Değişkenler İçin Korelasyon Matrisi
Şekil 3.1’de TV ile sales değişkenleri arasında güçlü doğrusal bir ilişki gözlemlenmektedir.
Sadece TV ve sales değişkenlerinden oluşan yeni bir data frame oluşturalım.
df1 <- data.frame(sales = df$sales,TV = df$TV)
library(knitr)
kable(head(df1,6)) # Yeni oluşturduğumuz veri setinin ilk 6 satırı.| sales | TV |
|---|---|
| 22.1 | 230.1 |
| 10.4 | 44.5 |
| 9.3 | 17.2 |
| 18.5 | 151.5 |
| 12.9 | 180.8 |
| 7.2 | 8.7 |
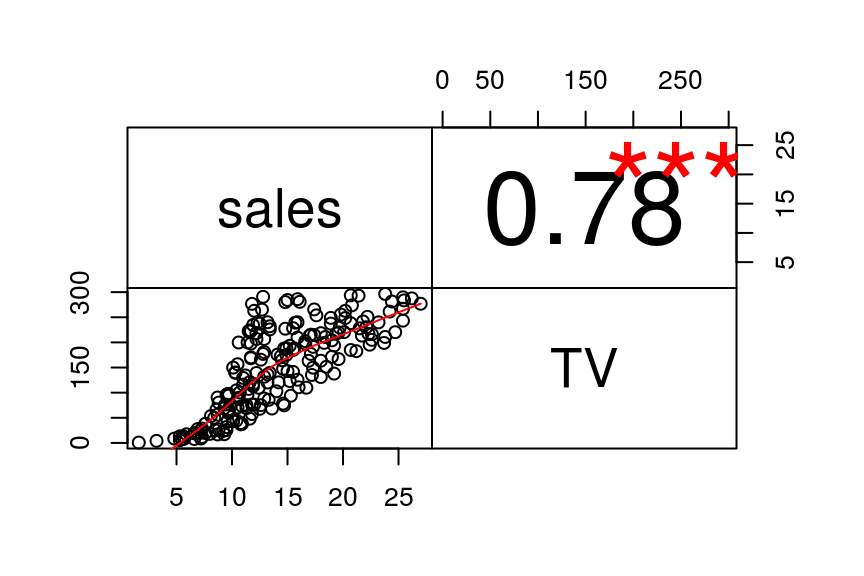
Şekil 3.2: sales~TV Değişkenleri Arasındaki Korelasyon Matrisi
Şekil 3.2’de görüldüğü gibi sales ve TV değişkenleri arasında doğrusal bir ilişki vardır.
Grafikte gözükse de cor() fonksiyonu yardımıyla sales ve TV değişkenleri arasındaki korelasyona ulaşılabilir.
## [1] 0.7822244TV’ye verilen reklam ile Satışlar arasında güçlü bir ilişki olduğunu görüyoruz. Bu değişkenler ile regresyon modeli kurabiliriz. Reklamların satışlar üzerindeki etkisini araştırıdğımız için X = TV(bağımsız değişken), Y = Sales(bağımlı değişken) olarak belirleyebiliriz.
3.1 Model Katsayılarının Tahmini
\[\begin{equation} \hat{\beta}_{1}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \end{equation}\]
## [1] 0.04753664\[\begin{equation} \hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1} \bar{x} \end{equation}\]
## [1] 7.032594Bulduğumuz katsayılar ile aşağıdaki eşitlik yazılabilir.
\[\begin{equation} \text { sales } \approx 7.032594+ 0.04753664 \times \mathrm{TV} \end{equation}\]
Yukarıdaki eşitliği yorumlayacak olursak. TV değişkenindeki 1 birimlik değişiklik sales değişkeninde 0.04753664 birimlik değişikliğe neden olur.
Bulduğumuz katsayılar ile regresyon doğrusunu çizdirecek olursa;
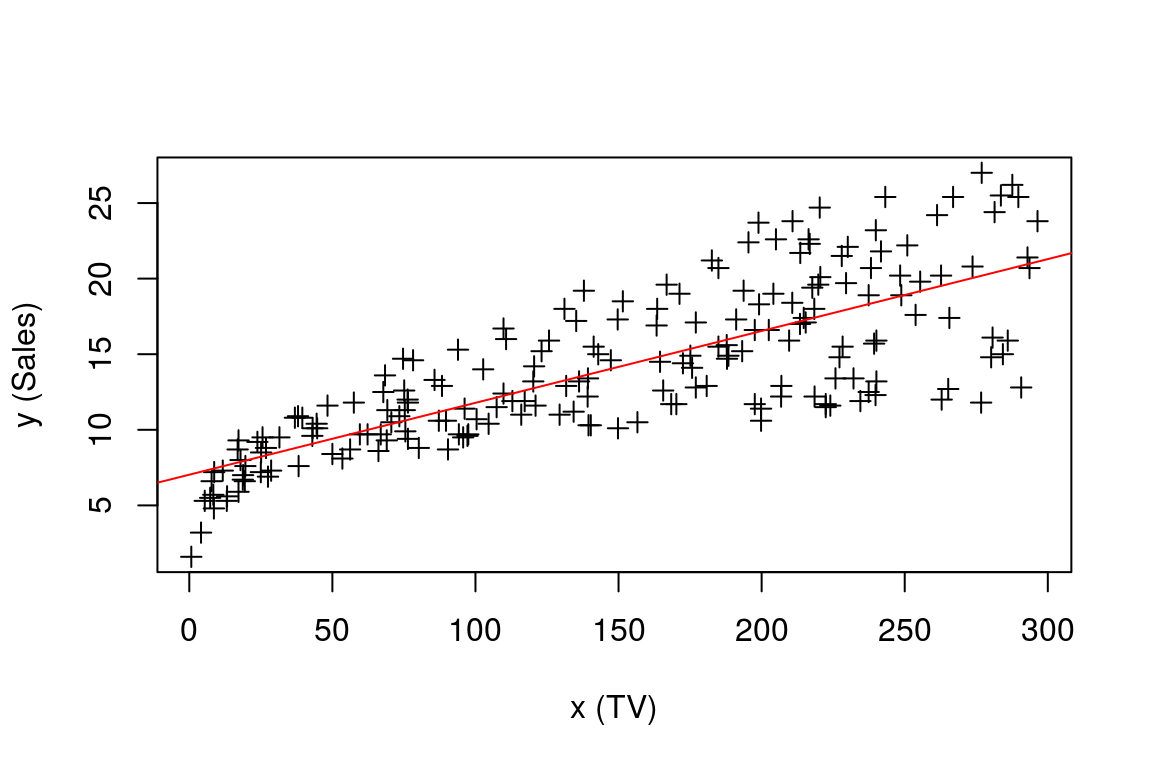
Şekil 3.3: Regresyon Doğrusu
3.2 Katsayıların ve Artıkların Varyansı
3.2.1 Artıkların Varyansı
\[\begin{equation} \mathrm{RSE}=\sqrt{\mathrm{RSS} /(n-2)} \end{equation}\]
\(RSS\)
## [1] 2102.531\(RSE\)
## [1] 3.2586563.2.2 Katsayıların Varyansları
\[\begin{equation} \operatorname{SE}\left(\hat{\beta}_{0}\right)^{2}=\sigma^{2}\left[\frac{1}{n}+\frac{\bar{x}^{2}}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\right], \quad \operatorname{SE}\left(\hat{\beta}_{1}\right)^{2}=\frac{\sigma^{2}}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \end{equation}\]
\(\beta_{0}\)’ın standart hatası;
varbeta0 <- rse^2*(1/length(x) + (mean(x)^2)/ sum((x-mean(x))^2)) # beta 0'ın varyansı
se_beta0 <- sqrt(varbeta0)
se_beta0## [1] 0.4578429\(\beta_{1}\)’in standart hatası;
## [1] 0.0026906073.3 Katsayılar İçin Güven Aralığı
\(\hat{\beta}_{1}\) için %95 güven aralığı; \[\begin{equation} \hat{\beta}_{1} \pm 2 \cdot \operatorname{SE}\left(\hat{\beta}_{1}\right) \end{equation}\]
beta1_alt_limit <- b_1 - 2 * se_beta1
beta1_ust_limit <- b_1 + 2 * se_beta1
beta1_ga <- c(beta1_alt_limit,beta1_ust_limit)
names(beta1_ga) <- c("Alt Limit","Üst Limit")
beta1_ga## Alt Limit Üst Limit
## 0.04215543 0.05291785\(\hat{\beta}_{0}\) için %95 güven aralığı; \[\begin{equation} \hat{\beta}_{0} \pm 2 \cdot \operatorname{SE}\left(\hat{\beta}_{0}\right) \end{equation}\]
beta0_alt_limit <- b_0 - 2 * se_beta0
beta0_ust_limit <- b_0 + 2 * se_beta0
beta0_ga <- c(beta0_alt_limit,beta0_ust_limit)
names(beta0_ga) <- c("Alt Limit","Üst Limit")
beta0_ga## Alt Limit Üst Limit
## 6.116908 7.9482793.4 Katsayıların ve Modelin Anlamlılığı
3.4.1 Katsayıların Anlamlılığı
Katsayıların anlamlılığını ölçmek için önce katsayıların t değerlerini bulmalıyız.
\(t=\frac{\hat{\beta}_{1}-0}{\operatorname{SE}\left(\hat{\beta}_{1}\right)}\)
## [1] 17.66763## [1] 15.360283.4.2 t tablo değerinin bulunması
## [1] -1.972017## [1] 1.9720173.4.3 Hipotezler
\(H_{0}: \beta_{1}=0\) \(H_{A}: \beta_{1} \neq 0\)
Çift taraflı yapılan hipotez testinde \(\hat{\beta}_{1}\) ve \(\hat{\beta}_{0}\) mutlak değerce 0.05 anlamlılık düzeyinde tablo değerimizden büyük olduğu için \(H_{0}\) hipotezi reddedilir. Katsayılarımız anlamlıdır.
Ayrıca hesapladığımız \(\hat{\beta}_{0}\) ve \(\hat{\beta}_{1}\) değelerleri, hesapladığımız %95 güven aralıklarının içinde olduğu için de anlamlı olduklarını söyleyebiliridk.
## Alt Limit Üst Limit
## 0.04215543 0.05291785## [1] "Beta1: 0.0475366404330197"## Alt Limit Üst Limit
## 6.116908 7.948279## [1] "Beta0: 7.03259354912769"3.5 \(R^{2}\) Modelin Açıklayıcılığı
Modelin genel olarak anlamlığını incelemek içi \(R^{2}\) değerinden yararlanılabilir.
\[\begin{equation} R^{2}=\frac{\mathrm{TSS}-\mathrm{RSS}}{\mathrm{TSS}}=1-\frac{\mathrm{RSS}}{\mathrm{TSS}} \end{equation}\]
## [1] 0.6118751Aynı değeri \(X\) ve \(Y\) değişkenlerinin aralarındaki korelasyonun karesiyle de bulabiliriz.
\[\begin{equation} \operatorname{Cor}(X, Y)=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}} \end{equation}\]
## [1] 0.6118751Katsayılarımız anlamlı ancak modelimizin çok iyi sonuçlar vereceğini söyleyemeyiz.