2 Basit Doğrusal Regresyon

2.1 Basit Doğrusal Regresyon Modeli ve Katsayılar

Uyarı: Bu bölümde Basit Doğrusal Regresyon hakkında bazı temel bilgiler verilecektir, sadece uygulama ile ilgilenenler, R ile Basit Doğrusal Regresyon Uygulaması kısmına geçebilir.

Not: Daha detaylı öğrenmek için İlker Birbil’in Youtube’da, Veri Defteri kanalındaki Doğrusal Bağlanım 1-2 videolarını izlemelerini tavsiye ederim. Ayrıca kaynakça kısmından da yararlandığım kaynakları kurcalayabilirsiniz.

2.1.1 Basit Doğrusal Regresyon Modeli

Basit doğrusal regresyon modeli, tek bir açıklayıcı(bağımsız) değişken ile açıklanan(bağımlı) değişken arasında doğrusal(lineer) bir ilişki olduğunda, açıklayıcı(bağımsız) değişken yardımıyla açıklanan(bağımlı) değişkeni tahmin etmek(öngörmek) için kullanılan bir yöntemdir.

$$\begin{equation} Y=\beta_{0}+\beta_{1} X+\epsilon \end{equation}$$

Yukarıdaki denklem ile doğrusal bir model kurabiliriz. Bu modelde $\beta_{0}$ kesim noktası, $\beta_{1}$ doğrunun eğimi,$\epsilon$ hata terimidir.

Bir pazarlama firması televizyon, gazete ve radyoya verdiği reklamların satışlar üzerindeki etkisini araştırıyor olsun.

$$\begin{equation} \text { sales } \approx \beta_{0}+\beta_{1} \times \mathrm{TV} \end{equation}$$

sales ve TV değişkenleri arasındaki doğrusal model yukarıdaki gibi olur.

$$\begin{equation} \hat{y}=\hat{\beta}_{0}+\hat{\beta}_{1} x + e \end{equation}$$

Yukarıdaki denkleme, örneklem regresyon fonksiyonu(ÖRF) denir.Burada $X$$=$$x$ durumunda, $\hat{y}$ $Y$’nin tahmincisi, $\hat{\beta}_{0}$ kesim noktasının($\beta_{0}$) tahmincisi, $\hat{\beta}_{1}$ doğrunun eğim($\beta_{1}$) tahmincisidir, $e$ ise artıktır.

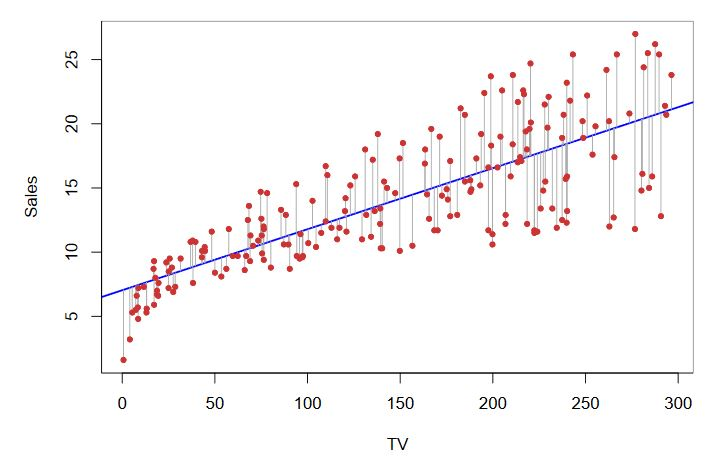
Şekil 2.1: Basit Doğrusal Regresyon Modeli-1

2.1.2 Artıklar

Örneklem regresyon fonksiyonu(3) yardımıyla bulunan öngörü değerleri ile gerçek değerlerin arasındaki farka artıklar(residuals) denir. $i$. artık; $e_{i}=y_{i}-\hat{y}_{i}$ formülü ile hesaplanır.

Artık(Hata) Kareler Toplamı(AKT)($residual sum of squares (RSS)$)

$\mathrm{RSS}=e_{1}^{2}+e_{2}^{2}+\cdots+e_{n}^{2}$

$\operatorname{RSS}=\left(y_{1}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{1}\right)^{2}+\left(y_{2}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{2}\right)^{2}+\ldots+\left(y_{n}-\hat{\beta}_{0}-\hat{\beta}_{1} x_{n}\right)^{2}$

2.2 En Küçük Kareler Yöntemi (EKK)

En küçük kareler yöntemi hata kareleri minimum yapmak üzerine kuruludur. Hata kareler toplamı dış bükey bir fonksiyondur. Minimum yapmak için hata kareler toplamının türevi alınır. Bu yöntem yardımıyla $\hat{\beta}_{0}$ ve $\hat{\beta}_{1}$ katsayıları tahmin edilir.

2.2.1 Katsayıların Tahmini

$$\begin{equation} \hat{\beta}_{1}=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \end{equation}$$

$$\begin{equation} \hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1} \bar{x} \end{equation}$$

Burada $\bar{y} \equiv \frac{1}{n} \sum_{i=1}^{n} y_{i}$ ve $\bar{x} \equiv \frac{1}{n} \sum_{i=1}^{n} x_{i}$ şeklindedir.

2.3 Artıkların ve Katsayıların Varyansı

2.3.1 Katsayıların Varyansı

Katsayıların varyansı aşağıdaki formüller ile hesaplanabilir;

$$\begin{equation} \operatorname{SE}\left(\hat{\beta}_{0}\right)^{2}=\sigma^{2}\left[\frac{1}{n}+\frac{\bar{x}^{2}}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}}\right], \quad \operatorname{SE}\left(\hat{\beta}_{1}\right)^{2}=\frac{\sigma^{2}}{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \end{equation}$$

2.3.2 Artıkların Varyansı

Artıkların varyansı elimizdeki veri yardımıyla tahmin edilebilir. Bu tahmine artıkların standart hatası denir($residual standard error$). Aşağıdaki formül ile hesaplanabilir;

$$\begin{equation} \mathrm{RSE}=\sqrt{\mathrm{RSS} /(n-2)} \end{equation}$$

2.3.3 Güven Aralıkları

$\hat{\beta}_{1}$ için %95 güven aralığı; $$\begin{equation} \hat{\beta}_{1} \pm 2 \cdot \operatorname{SE}\left(\hat{\beta}_{1}\right) \end{equation}$$

$\hat{\beta}_{0}$ için %95 güven aralığı; $$\begin{equation} \hat{\beta}_{0} \pm 2 \cdot \operatorname{SE}\left(\hat{\beta}_{0}\right) \end{equation}$$

2.4 Katsayıların ve Modelin Anlamlılığı

Oluşturulan modelde katsayıların ve modelin genel olarak anlamlılığı test edilmelidir.

2.4.1 Katsayıların Anlamlılığı

Katsayıların anlamlı olup olmadığını test etmek için hipotez testlerinden yararlanılır. Hipotezler aşağıdaki gibi kurulur;

$H_{0}:$ $X$ ve $Y$ arasında ilişki yok. $H_{A}:$ $X$ ve $Y$ arasında ilişki var.

$H_{0}: \beta_{1}=0$ $H_{A}: \beta_{1} \neq 0$

(Bu hipotez ile parametrelerimizin $0$’a eşit olup olmadığına bakılır.)

Hipotez testini yapmak için $t$ değerini aşağıdaki formül ile hesaplanabilir.

$t_{c}=\frac{\hat{\beta}_{1}-0}{\operatorname{SE}\left(\hat{\beta}_{1}\right)}$

$$\begin{equation} \left|t_{c}\right|>t_{\frac{\alpha}{2}}, n-(k+1) \end{equation}$$

Hesapladığımız $t$ değeri, tablodaki $t$ değerinden büyükse $H_{0}$ hipotezi reddedilir. $H_{0}$ hipotezi reddedildiğinde, test edilen katsayıya anlamlıdır denilir.

2.4.2 Model Anlamlılığı

Modelin genel olarak anlamlılığını da incelemek gerekir. Bunun için F istatistiği değerine bakılabilir.

$H_{0}:$ Model anlamlı değildir. $H_{A}:$ Model anlamlıdır.

Hesaplanan F değeri tablodaki F değerinden büyük ise $H_{0}$ hipotezi reddedilir. Model anlamlıdır denir. F değeri aşağıdaki formül ile hesaplanır.

$$\begin{equation} F_{c}=\frac{S S_{R e g} / k}{S S_{R e s} / n-(k+1)} \end{equation}$$ (Burada k bağımsız değişken sayısıdır, basit doğrusal regresyonda bir tane bağımsız değişkenimiz olduğu için değeri 1’dir.)

F tablo değeri ise 0.05 anlamlılık düzeyinde aşağıdaki gibi bulunur. $$\begin{equation} F_{t}=F_{0.05, k, n-(k+1)} \end{equation}$$ (Burada da k değerini 1 alıyoruz.)

$$\begin{equation} F_{c}>F_{t} \end{equation}$$

Yukarıdaki eşitlik sağlanırsa $H_{0}$ hipotezi reddedilir ve model anlamlıdır denilir.

$S S_{R e g}$ ve $S S_{R e s}$’in nasıl bulunduğuna daha detaylı olarak Çoklu Doğrusal Regresyonda değinilecektir. Şimdilik F değerinin 60-70 gibi değerlerden yüksek olduğunda modelin anlamlı olduğunu düşünebilirsiniz.

2.4.3 $R^{2}$ ile Modelin Açıklayıcılığı

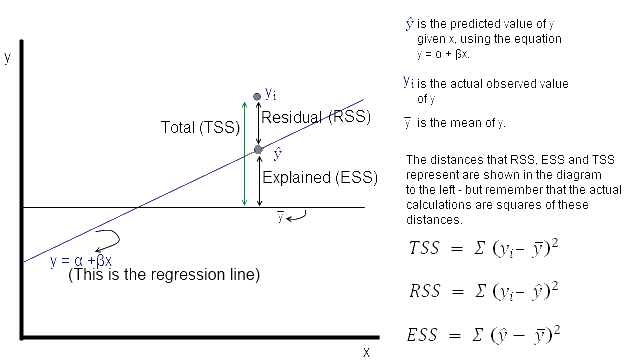
Şekil 2.2: TSS, RSS, ESS

$TSS$(Total Sum of Squares): Toplam Kareler Toplamı $RSS$(Residuals Sum of Squares): Artık Kareler Toplamı $ESS$(Explanied Sum of Squares): Açıklanan Kareler Toplamı

Modeldeki bağımsız değişkenlerin, bağımlı değişkeni ne kadar açıkladığı $R^{2}$ değeri ile ölçülebilir. Bu değer 0 ile 1 arasında değer alır. $R^{2}$ değerinin 1’e yakın olması bağımsız değişkenlerin, bağımlı değişkenleri iyi bir şekilde açıkladığını gösterir. Aşağıdaki formül yardımıyla $R^{2}$ değeri bulunabilir.

$$\begin{equation} R^{2}=\frac{\mathrm{TSS}-\mathrm{RSS}}{\mathrm{TSS}}=1-\frac{\mathrm{RSS}}{\mathrm{TSS}} \end{equation}$$

Ayrıca $R^{2}$$=$$r^{2}$ eşitliği vardır. Yani $X$ ve $Y$ arasındaki korelasyon katsayısının karesi $R^{2}$ değerini verir.

$$\begin{equation} \operatorname{Cor}(X, Y)=\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)}{\sqrt{\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}} \end{equation}$$