Chapter 2 Forest Runoff Control
The chapter outlines the influence of forests on runoff formation in torrential catchments and their effect on flood events - without addressing the role of available sediment.


Figure 2.1: Torrential flood event, July \(7^th\) 2016; Pockaubach (AUT)
Torrents are characterized by highly variable discharges and sediment transport volumes with bedload constituting a substantial part of the total load (Church and Jakob 2020; K.-H. Schmidt and Ergenzinger 1994). Although only a tiny fraction of the world’s fresh water is found on the surface – Hewlett (1982) describes about \(75\%\) of all precipitation in temperate climates become soil water either as soil moisture or groundwater – many torrential flood events relate to quantity, timing and energy disposition of surface runoff.
In contrast to static river floods, torrential floods are defined as constantly or temporarily flowing watercourses with strongly changing perennial or ephemeral discharge and intermittent flow conditions, originating within small and steep torrential catchments (ONR-24800 2009).
One of the essential protective functions of forests in steep alpine catchments is the generation, attenuation, or prevention of surface flow (Figure 2.2) caused by short but extreme rainfall events.


Figure 2.2: Surface flow and traces of surface flow
Considering Figure 2.3, all precipitation \(P\) that is not stored, at least temporarily, contributes to runoff. Some precipitation is stored as [interception][Interception] on the leaves of plants in the various vegetation layers, some is throughfall and stemflow, and some is evaporated from the leaves or soil. Rain that falls on the soil surface is divided into surface runoff and percolating water, some of which is stored in litter and topsoil and becomes subsurface (interflow) runoff.
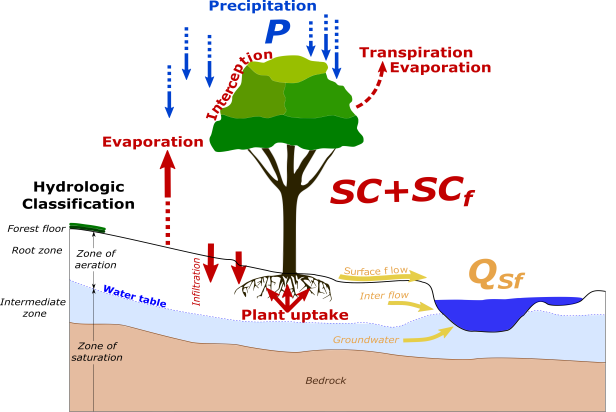
Figure 2.3: Waterbalance in forests
2.1 Canopy storage
Interception (\(I\), mm) is described as the fraction of rainwater retained in the tree canopy, (defined by canopy storage \(S_c\), mm), and on the litter (defined by litter storage \(S_l\), mm) until it evaporates back into the atmosphere.
\[\begin{equation} I=S_c+S_l \tag{2.1} \end{equation}\]
Thus, the process of total interception \(I\) represents a net loss to the hydrologic cycle in the watershed and can vary over a wide range based on the influencing factors described below.
In forests, however, storage in the canopy is of greater importance. The fraction of the gross rainfall (\(P_g\), mm) that remains due to interception (mainly based on canopy storage capacity) is defined as net rainfall (\(P_n\), mm) and depends on the amount of throughfall (\(T_h\), mm) plus stemflow (\(S_f\), mm).
\[\begin{equation} S_c=P_g-P_n=P_g-T_h-S_f \tag{2.2} \end{equation}\]
![Distribution of rainfall after it reached the canopy of 5 m tall manuka (Leptospermum scoparium). [after @Selby1982]](figures/interception_Selby.png)
Figure 2.4: Distribution of rainfall after it reached the canopy of 5 m tall manuka (Leptospermum scoparium). (after Selby 1982)
Throughfall (\(T_h\)) is defined as precipitation that passes through the vegetative canopy or as drip from vegetation, whereas stemflow (\(S_f\)) describes water that flows down the stems to the ground surface. Unlike precipitation, there are no standardized tools or sampling plans for measuring and monitoring throughfall in forested areas. Figure shows a simple method to measure the throughfall. For this purpose, collecting pipes with a known cross-section are set up at regular intervals under the canopy and the “throughfalling” amount of precipitation is measured. To measure stem flow, collars are attached to the trunks of trees to divert stem flow into measuring tanks.
In general, canopy storage capacity (\(S_c\)) increases exponentially during a thunderstorm until a critical capacity (maximum canopy storage capacity \(S_{c(max)}\), mm) is reached and the weight of further rain overcomes the surface tension that holds water on plants (c.f. Figure 2.4).
As long as the canopy is unsaturated, i.e. the canopy storage capacity \(S_c\) has not yet been reached, most of the rain can be stored. After \(S_c\) is reached, most of the rain runs off onto the ground, and the interception loss can only be increased by evaporation during the rain. Canopy interception loss (\(I_c\), mm) can thus be expressed as evaporation during rainfall (\(E\), mm/h) and the amount of water which can be evaporated from the canopy after the rain - which is equal to the canopy storage capacity (\(S_c\)) (Klaassen, Bosveld, and de Water 1998).
\[\begin{equation} I_c=E\cdot t+S_c \tag{2.3} \end{equation}\]
For torrential flood events, the gross rainfall \(P_g\) can be assumed to be sufficiently large enough to meet the maximum storage capacity of the tree canopy \(S_{c(max)}\). Alpine forests can hold back up to 6 mm of water in the canopy during a single precipitation event (Breitsameter 1996; Markart 2000; Weiskopf 2002) (c.f. Figure 2.5)
![Canopy storage capacities of spruce and beeches as a function of gross rainfall [after @Lang1970]](figures/Scmax.png)
Figure 2.5: Canopy storage capacities of spruce and beeches as a function of gross rainfall (after Lang 1970)
For this reason, it is often assumed that the evaporation of water stored in the canopy after the rainfall event (\(S_c\)) is equal to the maximum canopy storage capacity (\(S_{c(max)}\)). However, if the gross rainfall is below the maximum canopy storage capacity, the amount of evaporation of water in the canopy can be described by an exponential form, as indicated in Figure (2.4). \[\begin{equation} S_c=S_{c(max)}(1-e^{-\tau P_g}) \tag{2.4} \end{equation}\] With \(\tau\), a fitting parameter that, theoretically, describes the fraction of \(P_g\) which becomes free throughfall or/and stemflow.
2.1.1 Mechanisms controlling canopy storage capacity
The main factors controlling the canopy storage capacity \(S_c\) are mainly due to meteorological and vegetation characteristics.
2.1.1.1 Meteorology
Meteorological effects on the interception performance can be rain intensity, rain duration, precipitation form, but also wind speed and pre-wetting conditions.
- Low precipitation intensity leads to the interception of a large portion of precipitation. Thus, frequent and light precipitation can result in high interception losses by converging to \(S_{c(max)}\). For very short, low-intensity precipitation events, even almost all of the precipitation can be intercepted, i.e., there is no throughfall or stemflow.(\(S_{c(max)}\) reached)
- Although a large proportion of precipitation will be intercepted during a very short storm, absolute interception storage increases with increasing storm duration.
- However, as \(S_c\) decreases exponentially, a larger fraction is intercepted during short precipitation events compared to long duration thunderstorms where interception reaches an equilibrium state (maximum canopy storage capacity) (c.f. Figure 2.4).
- Wind speed can affect canopy water holding capacity (resulting in a decrease of \(S_c\)) and canopy/(litter) interception loss by promoting evaporation (resulting in an increase of \(S_c\)).
- Liquid precipitation forms a first layer earlier than snow (due to higher surface tension), to which the subsequent rain adheres.
- At temperatures around 0°C, rain can freeze to the plants.
- Snow, on the other hand, is more easily blown away or removed from plants, but solid snowflakes can also bridge gaps between leaves/needles, stems, and branches, so the canopy storage effect of especially wet snow can be considerable.
2.1.1.2 Vegetation
Structural vegetation features are the main factors influencing interception performance. These include tree species-specific parameters such as size, flexibility, strength and pattern of the branches or texture, surface and orientation of the leaves/needles, and on the other hand, stand and vertical structures and the formation of the herb layer.
- Canopy storage capacity depends on the tree species and age (density of canopy).
![Interception capacity of different tree species and ages [after @Mitscherlich1971]](figures/interc1.png)
Figure 2.6: Interception capacity of different tree species and ages (after Mitscherlich 1971)
- Canopy storage capacity can further be represented as a function of Leaf Area Index (LAI). \[\begin{equation} S_c=\alpha \cdot LAI \tag{2.5} \end{equation}\] with \(\alpha=0.15\) for broadleaved and \(\alpha=0.20\) for coniferous tree species.
![Typical LAI values of different vegetation units and altitudes. [after Aulitzky 1969?]](figures/BFI.png)
Figure 2.7: Typical LAI values of different vegetation units and altitudes. [after Aulitzky 1969?]

Figure 2.8: Canopy storage capacity of different tree species and ages
2.1.2 Horizontal Interception
Markart, Kohl, and Perzl (2007) assume that due to the interception effect of forest stands in the Eastern Alps, about \(\frac{1}{5}\) to \(\frac{1}{3}\) of the annual precipitation never reaches the ground.
2.2 Evapotranspiration
Evapotranspiration of forests is in general mainly controlled by the tree species as well as stand density and stand age. Evergreen coniferous species, which are dominate in Austria’s protective forests, transpire significant amounts of water even in winter compared to deciduous tree species. Thus, the runoff disposition of coniferous forests is lower in the early spring and late fall compared to deciduous forests and especially to the surrounding open land. Annual evapotranspiration of a forest stand was found to be twice to four-times higher compared to alpine grasslands (Fig. 2.9) (Zhang, Dawes, and Walker 2001; Markart, Kohl, and Perzl 2007).
![Relationship between annual evapotranspiration and rainfall for different vegetation type [@Zhang2001]](figures/evapotranspiration.png)
Figure 2.9: Relationship between annual evapotranspiration and rainfall for different vegetation type (Zhang, Dawes, and Walker 2001)
Due to the high intensity of extreme rainfall events causing torrential floods, in combination with the comparatively low interception capacity as well as the defacto non-existing evapotranspiration capacity due to high humidity, it can generally be assumed that direct effects like interception or evapotranspiration play a rather minor role. This is different when longer periods are considered – as for instance if the storage capacity in a torrent catchment is significantly affected by antecedent precipitation events. Here, direct effects of forests by evapotranspiration and interception can contribute by draining the soil storage capacity more quickly.
2.3 Forest soil storage
The impact of forests on surface flow as well as interflow is mainly controlled by the infiltration of water into the forest soil. Infiltration describes the process of water (precipitation) penetrating from the surface into the subsurface (soil).The volume of water infiltrated in a given period of time is known as the infiltration rate \(f_t\), whereas the maximum infiltration rate at which water can enter a soil defines the infiltration capacity. When precipitation exceeds the infiltration capacity, surface runoff occurs. Thus the infiltration capacity of the forest soil governs frequency and magnitude of torrential floodings.
The rate of infiltration depends on:
- Properties of the (forest) soil (texture, structure, organic matter, impermeable layers, …)
- Diameter of the pores (micro-, meso-, macro-pores)
- Antecedent water content
- Vegetation cover
An estimate of the infiltration rate is often based on two models. One is the Green-Ampt Model and the other is the infiltration model according to Horton.
Humus in hardwood stands has very short infiltration rates which are much higher in conifers (spruce, pine), favored by the thatch effect in dense spruce stands without understory. On the other hand, a rough surface with dead wood, dense ground vegetation or blowdown has a retarding effect on runoff (Fig.1). A large portion of precipitation infiltrates into the soil along the roots, especially in tree species with stem runoff. These and macropores in the soil allow rapid infiltration, but also rapid interflow to the receiving water. Therefore, the respective tree species decisively determines the water distribution in the soil and the rapid deep percolation via its rooting pattern.
Based on a theoretical assessment of runoff reduction by forest, Badoux et al. (2006) describe the basic storage capacity (\(Q_S\)) as the sum of surface runoff (saturation excess overland flow) and quick lateral runoff in the soil:
\[\begin{equation}
Q_S=P-SC
\tag{2.6}
\end{equation}\]
Thus, the base storage capacity represents the theoretical potential of water storage of the considered catchment area without afforestation. However, in addition to higher biomass above and below the ground surface, forests have greater surface roughness, higher canopy cover (leaf area), and lower albedo than other land uses [16, 17]. Further, forest soils are characteristically covered by a high litter layer and have a high proportion of macropores caused by dead plants or root decay as well as bioturbation [18]. These conditions generally lead to a reduction of surface runoff and an increase in intermediate and groundwater runoff. Forests can thus decrease runoff by increasing the basic storage capacity.
\[\begin{equation}
Q_{Sf}=P-SC-SC_f
\tag{2.7}
\end{equation}\]
Relating the runoff coefficient \(C_r\), reflecting the basic storage capacity of a catchment,
\[\begin{equation}
C_r=\frac{Q_S}{P}
\tag{2.8}
\end{equation}\]
with the specific runoff coefficient \(C_{rf}\), which accounts for additional storage capacity of forest sites,
\[\begin{equation}
C_{rf}=\frac{Q_{Sf}}{P}
\end{equation}\]
the influence of a forest site on the runoff can theoretically be described by a runoff reduction ratio due to forest (\(r_f\)):
\[\begin{equation}
r_f=\frac{Q_{Sf}/P}{Q_S/P}=1-\frac{SC_f}{P-SC}
\tag{2.9}
\end{equation}\]
In general and under similar initial conditions, forest soils have a higher water storage capacity than grassland, pasture or cropland soils (Badoux et al. 2006).
Further, soil properties play a dominant role in the development of runoff-related natural hazard processes such as floods, debris flows, and hillslope debris flows.
The runoff reduction ratio (\(r_f\)), shows
***
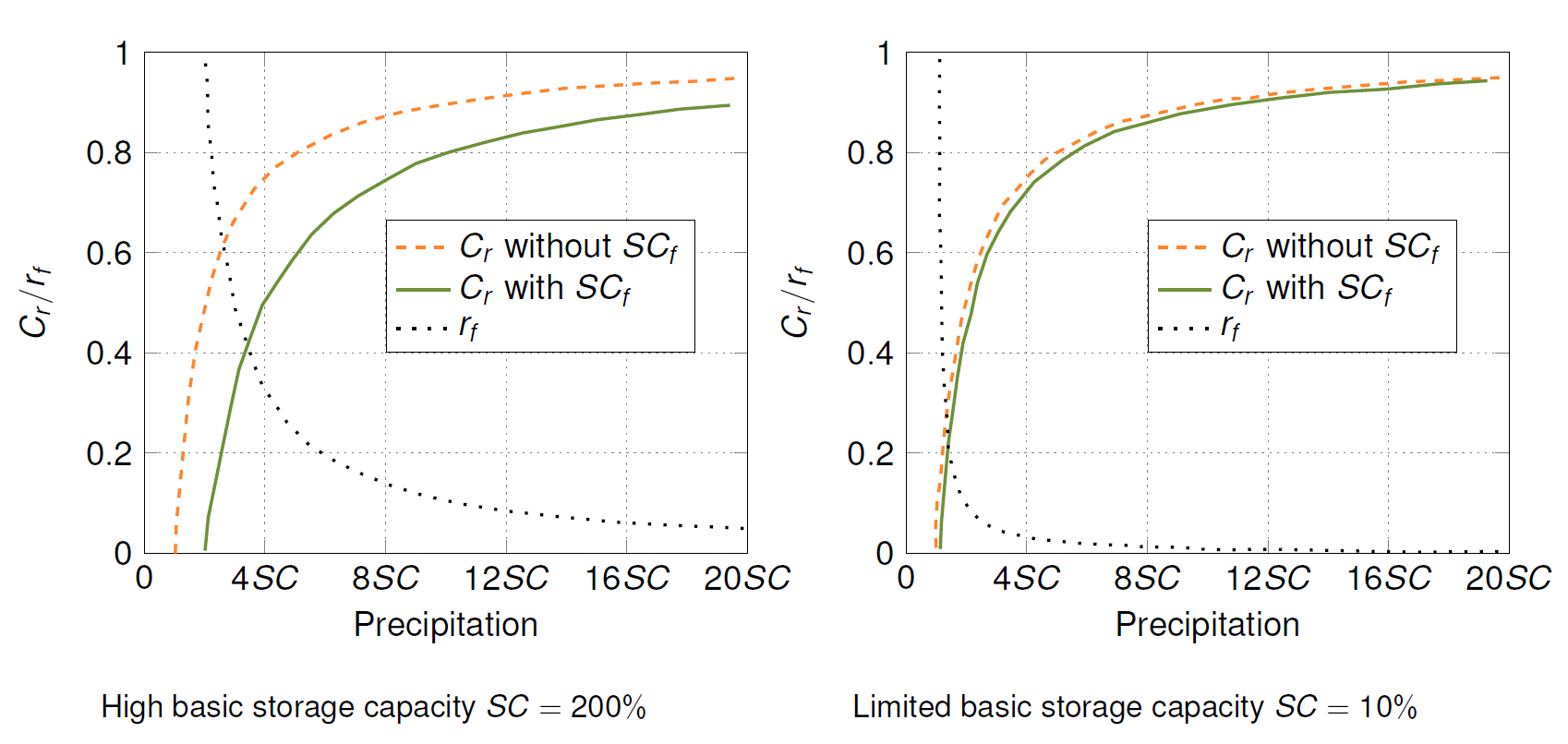
However, findings from paired catchment area studies show that forestry measures such as clear-cutting, afforestation and reforestation can have an influence on runoff [19]. While deforestation generally leads to an increase in mean annual runoff, peak runoff and runoff loads [20, 21], afforestation or reforestation by planting trees or restoring vegetation cover on degraded soils or meadows with native forests generally reduces runoff, peak flow, groundwater recharge and base flow, especially during the vegetation period.