4 Probabilidade Condicional
Probabilidade condicional é um dos conceitos mais importantes da teoria de probabilidades, pois frequentemente se quer calcular seu valor quando se tem alguma informação parcial a respeito do resultado de um experimento aleatório.
Além disso, mesmo quando não se tem essa informação parcial, as probabilidades condicionais muitas vezes são utilizadas para computar mais facilmente valores de probabilidades que se tem interesse.
Exemplo.4.1 A Tabela 4.1 mostra o resultado de um questionário aplicado a um grupo de 209 estudantes do Campus da UFC de Russas, em que foi perguntado o curso em que o discente está matriculado e se esse curso foi a sua primeira opção no processo seletivo ENEM.
Seja o experimento: escolher um dos 209 alunos ao acaso desse grupo e observar seu curso e se esse curso foi sua primeira opção no ENEM.
Considere a notação seguinte e Responda.
EP: Engenharia de Produção;
EC: Engenharia Civil;
ES: Engenharia de Software;
EM: Engenharia Mecânica e
CC: Ciências da Computação.
| Não foi primeira opção | Foi primeira opção | Total | |
|---|---|---|---|
| Ciência da Computação | 3 | 32 | 35 |
| Engenharia Civil | 4 | 7 | 11 |
| Engenharia de Produção | 11 | 47 | 58 |
| Engenharia de Software | 11 | 29 | 40 |
| Engenharia Mecânica | 7 | 58 | 65 |
| Total | 36 | 173 | 209 |
Note que a probabilidade está associada a frequência de estudantes com a característica desejada. Então tem-se o seguinte.
- Qual a probabilidade desse aluno ser do curso de Engenharia de Produção, tendo ou não sendo sua primeira escolha?
Resposta: \(P(EP)=\frac{58}{209} \approx 0,28\).
- Qual a probabilidade desse aluno ser do curso de Engenharia de Produção e esta ter sido sua primeira escolha no ENEM?
Resposta: \(P(EP\cap\mbox{Primeira Opção})=\frac{47}{209}\approx 0,22\).
- Dado que o estudante seja do curso de Engenharia de Produção, qual a probabilidade do curso ter sido sua primeira escolha?
Resposta: \(P(\mbox{Primeira Opção}|EP)=\frac{47}{58}\approx 0,81\).
Refaça o item (c) para os demais cursos.
\(P(\mbox{Primeira Opção}| CC)=\frac{32}{35} \approx 0,91\).
\(P(\mbox{Primeira Opção}| EC)=\frac{7}{11} \approx 0,64\).
\(P(\mbox{Primeira Opção}| ES)=\frac{29}{40} \approx 0,73\).
\(P(\mbox{Primeira Opção}| EM)=\frac{58}{65} \approx 0,89\).
4.1 Teorema do Produto
Para definir formalmente a probabilidade condicional, considere um experimento aleatório com espaço amostral \(\Omega\). Sejam \(A,B \subset \Omega\), então a probabilidade condicional do evento \(A\) dado que \(B\) ocorreu é definida como:
\[P(A|B)= \frac{P(A \cap B)}{P(B)}, \ \ \ \ \ P(B)>0,\] ou ainda
\[P(B|A)= \frac{P(A \cap B)}{P(A)}, \ \ \ \ \ P(A)>0.\]
Isso implica que \(P(A \cap B)= P(A|B)\cdot P(B) \Longrightarrow P(A \cap B)= P(B|A)\cdot P(A).\)
A relação acima é conhecida como Teorema do Produto.
\[P(\mbox{Primeira Opção}|EP)= \frac{P(\mbox{Primeira Opção}\cap EP)}{P(EP)}=\frac{\frac{47}{209}}{\frac{58}{209}}=\frac{47}{209} \times \frac{209}{58} \approx 0,81.\]
4.1.1 Diagrama de árvore
Muitas vezes o diagrama de árvore é útil no entendimento do espaço amostral do experimento, além de entender a obtenção dos valores de probabilidades associados aos eventos resultantes de realização conjunta de experimentos. Para entender a importância de uma árvore de probabilidades, considere o Exemplo 4.3.
- ambas sejam verdes.
Resolução: Para a primeira retirada, segue:
B: bola branca com \(P(B)=2/9\);
E: bola preta com \(P(E)=3/9\);
V: bola verde com \(P(V)=4/9\)
A árvore de possibilidades fica como mostra o diagrama.
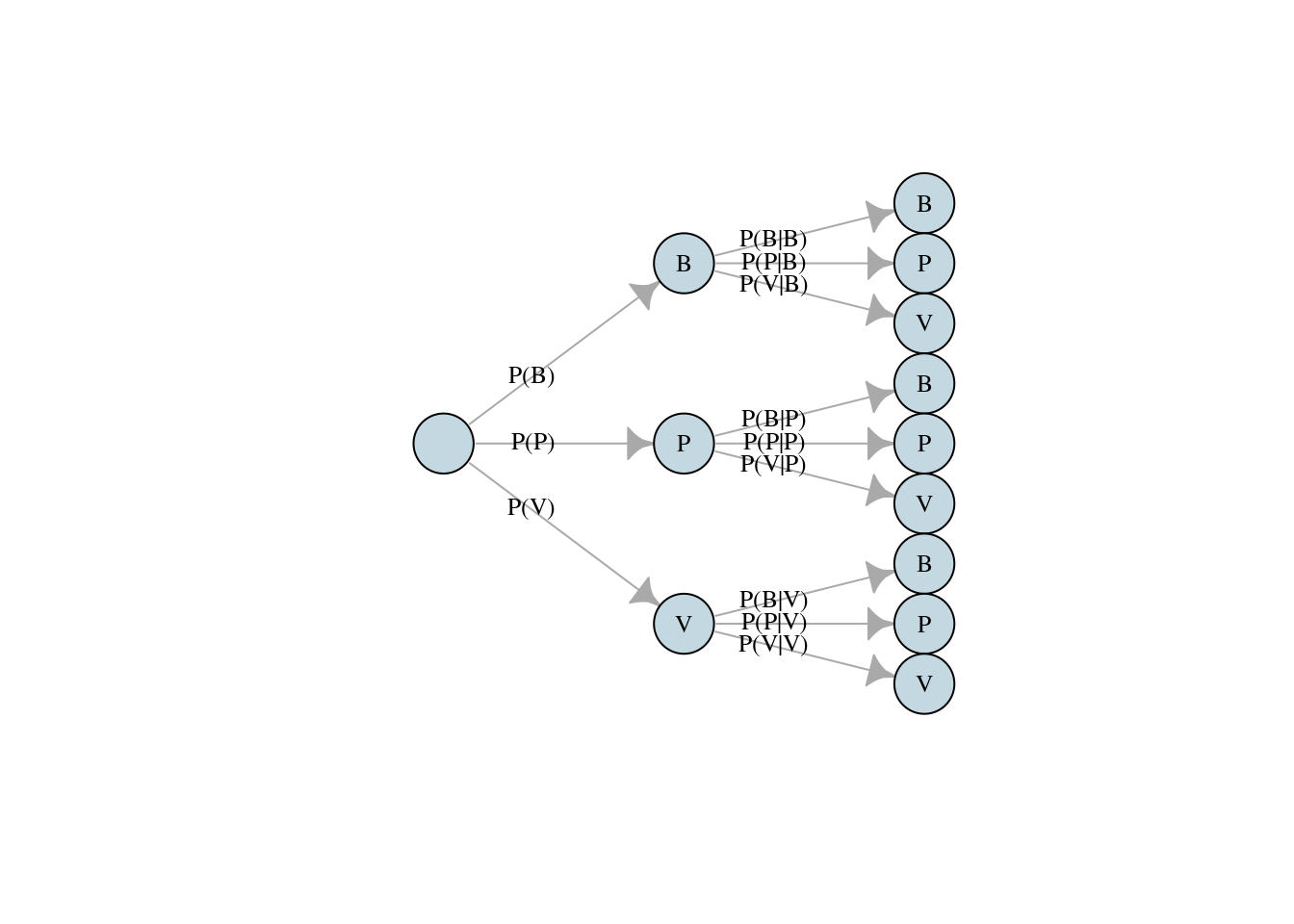
Pelo diagrama, é fácil notar que o espaço amostral do experimento é:
\[\Omega=\{BB, BP, BV, PB,PP,PV,VB,VP,VV \}\] Além disso,
\[P(VV)=P(V \cap V)= P(V)P(V|V)=\frac{4}{9}\times \frac{3}{8}\approx0,667\]
- ambas sejam da mesma cor.
Resolução:
\(P(BB)=P(B \cap B)= P(B)P(B|B)=\frac{2}{9}\times \frac{1}{8}\approx 0,278\) \(P(EE)=P(E \cap E)= P(E)P(E|E)=\frac{3}{9}\times \frac{2}{8}\approx 0,083\)
\[P(\mbox{ambas da mesma cor})= P(VV) +P(EE)+P(BB)=\frac{12}{72} + \frac{3}{72} + \frac{6}{72} = \frac{16}{72} \approx 0,22.\]
O Teorema do Produto pode ser generalizado da seguinte forma:
\[P\left(\bigcap_{i=1}^{n}A_i\right)= P(A_1)P(A_2|A_1)P(A_3|A_2\cap A_1) \ldots P(A_n|A_1 \cap \ldots \cap {A_{n-1}})\].
4.2 Lei da Probabilidade Total e Teorema de Bayes
Na prática, muitas vezes é útil ser capaz de derivar um conjunto de probabilidades condicionais a partir de um outro conjunto. Assim, o Teorema de Bayes relaciona probabilidades condicionais da forma \(P(A|B)\) com probabilidades condicionais da forma \(P(B|A)\), em que a ordem da condicionalidade é invertida.
A fim de apresentar esse teorema, considere uma sequência de eventos \(A_1,A_2, \cdots, A_n \subset \Omega\) tal que
\[A_i \cap A_j=\emptyset\] para todo \(i\neq j\). Ou seja, \(A_1,A_2, \cdots, A_n\) são dois a dois disjuntos, de modo que
\[\displaystyle\bigcup_{i=1}^{n} A_i=\Omega,\] Nesse caso \(A_1,A_2, \cdots, A_n\) forma uma partição de \(\Omega\), como mostrado na Figura
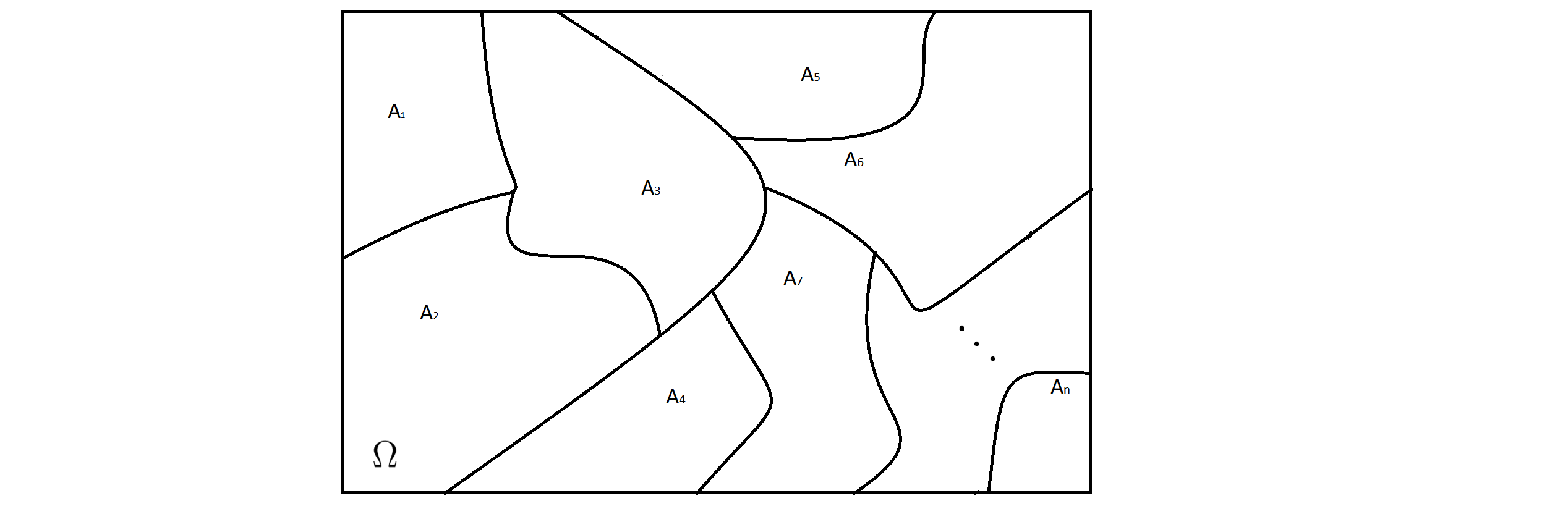
Figura 4.1: : Partição de um espaço amostral.
Considere um evento B qualquer tal que \(B \subset \Omega\), então B pode ser escrito como:
\[B=(B\cap A_1)\cup (B\cap A_2) \cup \cdots \cup (B\cap A_n).\]
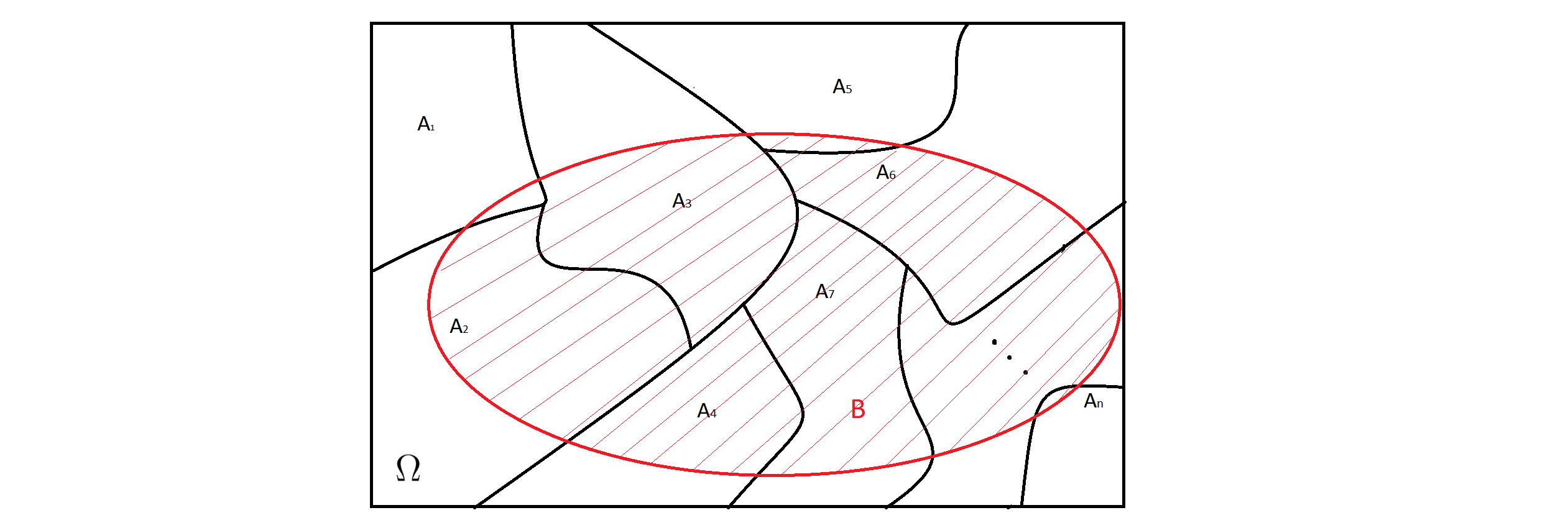
Figura 4.2: : Partição e um evento B qualquer.
Veja representações nas Figuras 4.1 e 4.2.
Deste modo, a probabilidade total de B pode ser obtida pelo axioma III da probabilidade, como segue. \[\begin{align} P(B)&={P}( B \cap A_1)+ {P}( B \cap A_2)+\ldots +{P}( B \cap A_n)\\ &=\displaystyle\sum_{i=1}^{n}{P}( B \cap A_i)\\ &=\displaystyle\sum_{i=1}^{n}{P}(B|A_i){P}(A_i). \end{align}\]
Essa expressão é conhecida como Lei da Probabilidade Total e possibilita a demostração de um importante teorema, chamado Teorema de Bayes.
Exemplo.4.4 Suponha que três máquinas (\(M_1, M_2\) e \(M_3\)) operem ao mesmo tempo. Considere que \(M_1, M_2\) e \(M_3\) sejam responsáveis por \(35\%, 40\%\) e \(25\%\) da produção total, respectivamente. Além disso, \(2\%\), \(3\%\) e \(1\%\) das peças da produção da máquina \(M_1, M_2\) e \(M_3\), respectivamente, saem com defeito. Ao final de um dia de produção, uma peça é sorteada ao acaso dessa linha de produção, qual a probabilidade de ser sorteada uma peça com defeito?
4.2.1 Teorema de Bayes
A partir da Lei da Probabilidade Total de um evento B numa partição \(A_1,A_2, \cdots, A_n\) de \(\Omega\), as probabilidades condicionais revesas \(P(A_j|B)\) para \(j = 1,2, \ldots ,n\), podem ser obtidas da seguinte forma:
\[\begin{eqnarray} {P}(A_j|B)= \frac{ {P}(B|A_j){P}(A_j)}{\displaystyle\sum_{i=1}^{n} {P}(B|A_i){P}(A_i)}, j=1,2, \ldots, n. \end{eqnarray}\]