3 Exemplo com dados reais
| Cidade | UF | Sexo | Curso |
|---|---|---|---|
| Limoeiro do Norte | CE | Feminino | Engenharia Mecânica |
| Aracati | CE | Feminino | Engenharia de Produção |
| Limoeiro do Norte | CE | Masculino | Engenharia de Produção |
| Quixadá | CE | Masculino | Engenharia Mecânica |
| Russas | CE | Masculino | Engenharia Mecânica |
| continua … | continua … | continua … | continua … |
Exemplo.3.1 Considere as variáveis “Sexo”, “Curso” e “Cidade” de estudantes do Campus da UFC de Russas, cujas primeiras 5 linhas das observações estão mostradas na Tabela 3.1. Considere, também, os seguintes eventos:
A= “estudantes do sexo Maculino”;
B= “estudantes que moram em Jaguaruana”;
C= “estudantes do curso de Engenharia Mecânica”.
Desse grupo de indivíduos, soreia-se um ao acaso (de modo que todos terão a mesma chance de ser escolhidos), qual a probabilidade de ser sorteado um aluno do sexo masculino e que seja do curso de Engenharia Mecânica?
Note que a probabilidade para cada evento está associada a frequência de estudantes com a característica no universo de estudantes. Assim, tem-se o seguinte.
Como são 209 indivíduos dos quais 59 são do curso de engenharia mecânica e do sexo masculino, essa probabilidade é dada por:
\[P(A \cap C)=\frac{\#(A \cap C)}{n}=\frac{56}{209} \approx 0,27.\] que é a frequência relativa de estudantes com a característica desejada na população.
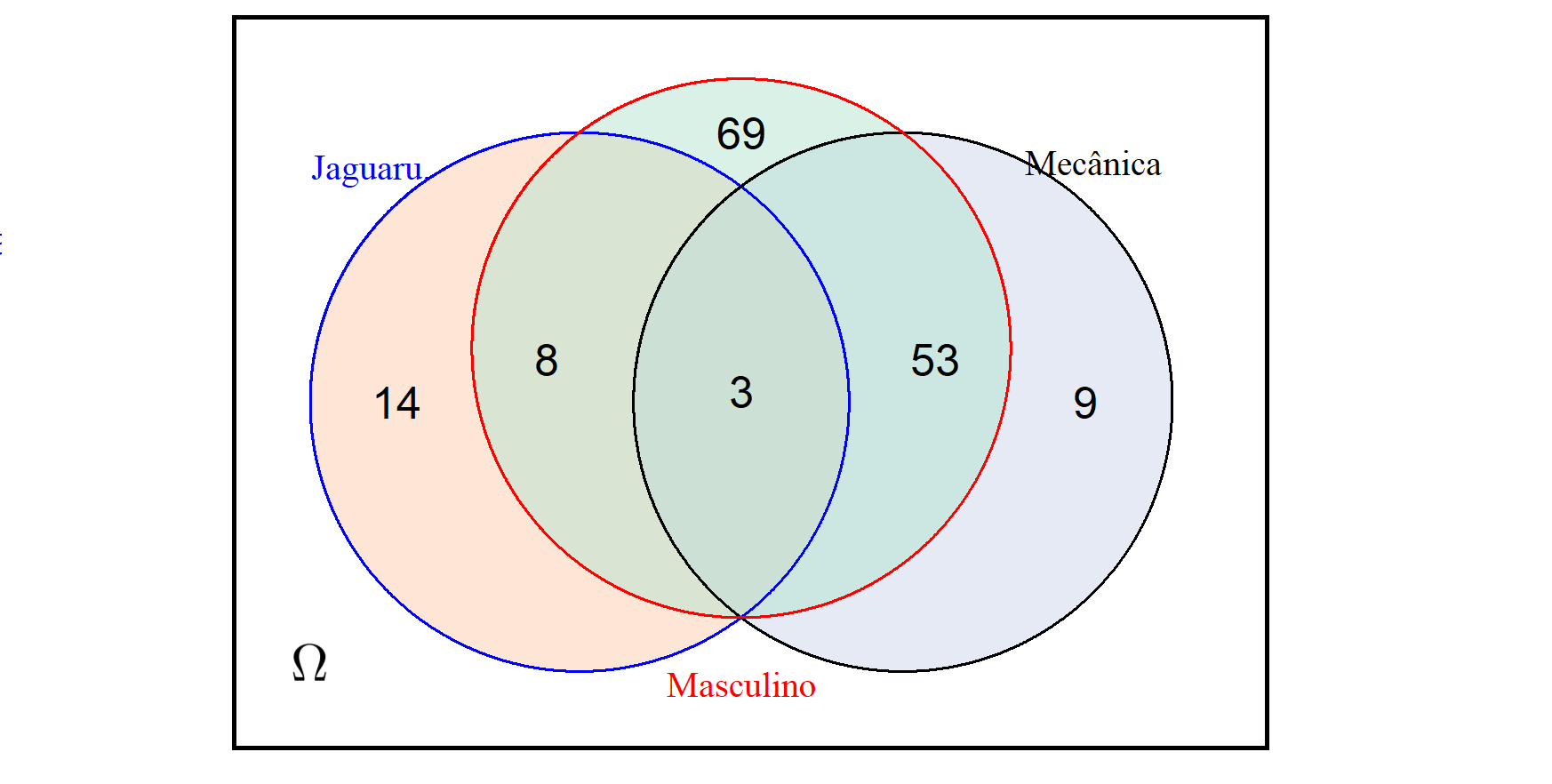
Figura 3.1: : Diagrama de Venn para os dados dos 209 estudantes que responderam ao questionário.