Chapter 3 Data manipulation & Inference I
In this chapter we will learn some useful tools for data manipulation and then go on to our first inferential statistics.
3.1 Data manipulation
In the previous chapter we have already done some exploratory analysis on our data but have skipped an important step that often comes before: In many cases we don’t have one tidy data set containing only the variables we are interested in. Often our data is scattered over multiple data sets and contains not only the variables or cases we are interested in, but a lot of unnecessary information.
The tidyverse (Wickham et al. 2019) is an R package that contains a lot of useful functions to deal with these problems, so we will start by installing and loading this package:
You can ignore all messages that are printed into the console upon loading the package.
3.1.1 Tibbles
We have provided you with two data sets to try out the data manipulation functions, data1.csv and data2.csv. Make sure the files are stored in your working directory folder and then read them in with:
Rows: 5 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
dbl (3): weight, age, id
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Rows: 5 Columns: 3
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (1): eyecolor
dbl (2): height, id
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Please make sure to use read_csv() and not read.csv(). While both are used to read csv-files into R, the former is a special tidyverse function that gives your data.frame a couple of nice extra features.
The first thing you will notice is the information given about the column specification while reading in the data. Here you can already check if the data type R chose for each column makes sense to you. dbl stands for double, which is a form of numeric vector, so in principle everything looks fine apart from the variable id which even though it contains numbers shouldn’t be a numeric / double because you can not really make computations with id-numbers. You can fix this issue with the following lines:
[1] "character"[1] "character"What you did there is converting the variable d1$id from a numeric to a character and then storing this new version in place of the old version of d1$id.
If you look at the type of d1 using class(), you can see that it is more than just a data.frame, it is for example also a tbl which is short for tibble.
[1] "spec_tbl_df" "tbl_df" "tbl" "data.frame" Basically a tibble can be used for everything a data.frame can be used for, but has some nice additional properties, for example they look nicer when printed to the console.
# A tibble: 5 × 3
weight age id
<dbl> <dbl> <chr>
1 85 34 1
2 56 72 2
3 73 33 3
4 76 45 4
5 60 23 5 3.1.2 Select and Filter
The first two functions for data manipulation are select(), which allows you to keep only certain variables (i.e. columns) and filter(), which allows you to keep only certain rows.
As its first argument, select() takes a data.frame or tibble and as its second argument the names of the variables you want to keep. Although it is technically not needed, we recommend bundling together the variable names in a vector:
# A tibble: 5 × 2
id age
<chr> <dbl>
1 1 34
2 2 72
3 3 33
4 4 45
5 5 23It is also possible to specify the variables you want to throw out instead, by putting a - before their names:
# A tibble: 5 × 1
age
<dbl>
1 34
2 72
3 33
4 45
5 23When you use filter() to chose only certain rows, you will mostly have some kind of rule which cases to keep. These rules are expressed as logical statements (see Chapter 1). For example the statement age > 40 would select all cases older than 40.
You can also connect multiple conditions: (age > 30) & (weight > 60) & (weight < 75) for example selects all cases that are older than 30 and weigh between 60kg and 75kg. filter() takes a tibble as its first and a logical expression as its second argument:
# A tibble: 1 × 3
weight age id
<dbl> <dbl> <chr>
1 73 33 3 It is also possible to select parts of your tibble or data.frame by simply listing the indices of the rows and columns you want to keep. This works similarly to subsetting a vector by using [<rows to keep> , <columns to keep>]:
# A tibble: 3 × 2
weight id
<dbl> <chr>
1 85 1
2 56 2
3 73 3 If you want to keep all columns or all rows, you leave the corresponding element in the [,] empty. You nevertheless have to keep the comma!
# A tibble: 1 × 3
weight age id
<dbl> <dbl> <chr>
1 85 34 1 # A tibble: 5 × 1
id
<chr>
1 1
2 2
3 3
4 4
5 5 3.1.3 Join
Another useful operation is the the join which allows you to join two data sets by a common key variable. d1 contains the weight and age of subject, while d2 contains their height and eye color. Let’s try to compute their body mass index. To do this, we need to join the two data sets because we need the weight and height information in one place. If you look at the IDs of the subjects you will notice that we cannot simply paste together those two tibbles because firstly the rows don’t have the right order and secondly each tibble contains one person that the other does not (id 5 and 6):
# A tibble: 5 × 3
weight age id
<dbl> <dbl> <chr>
1 85 34 1
2 56 72 2
3 73 33 3
4 76 45 4
5 60 23 5 # A tibble: 5 × 3
height eyecolor id
<dbl> <chr> <chr>
1 156 brown 2
2 164 blue 1
3 189 brown 4
4 178 green 3
5 169 blue 6 There are several ways to deal with this.
Inner join
The inner join only keeps cases (i.e. rows), that appear in both data sets. The function inner_join() takes two data.frames or tibbles and a string giving the name of the key variable that defines which rows belong together:
# A tibble: 4 × 5
weight age id height eyecolor
<dbl> <dbl> <chr> <dbl> <chr>
1 85 34 1 164 blue
2 56 72 2 156 brown
3 73 33 3 178 green
4 76 45 4 189 brown As you can see the cases 5 and 6 that only appeared in one of the data sets are left out of the result.
If the key variable has different names in the two data.frames, e.g. id and sno, you specify the by argument like this: by = c("id" = "sno").
Full Join
The opposite of the inner join is the full join. full_join() takes the same arguments as inner_join() but returns all cases. If a case does not appear in the other data set, the missing information is indicated with NA:
# A tibble: 6 × 5
weight age id height eyecolor
<dbl> <dbl> <chr> <dbl> <chr>
1 85 34 1 164 blue
2 56 72 2 156 brown
3 73 33 3 178 green
4 76 45 4 189 brown
5 60 23 5 NA <NA>
6 NA NA 6 169 blue Right and left join
The right and left join take one of the data sets fully and join only the rows from the other data set that fit this data set. That is, the right join takes the full right data set from the function call and attaches all fitting rows from the left data set, whereas the left join takes the full left data set from the function call and attaches all fitting rows from the right data set:
# A tibble: 5 × 5
weight age id height eyecolor
<dbl> <dbl> <chr> <dbl> <chr>
1 85 34 1 164 blue
2 56 72 2 156 brown
3 73 33 3 178 green
4 76 45 4 189 brown
5 60 23 5 NA <NA> # A tibble: 5 × 5
weight age id height eyecolor
<dbl> <dbl> <chr> <dbl> <chr>
1 85 34 1 164 blue
2 56 72 2 156 brown
3 73 33 3 178 green
4 76 45 4 189 brown
5 NA NA 6 169 blue 3.1.4 Creating new variables
Now that we have learned to join two data sets, let’s do a right join of d1 and d2 and use the resulting data set to compute the subjects’ BMI. First we save the joint data in a new variable d:
Then we compute the BMI according to the formula \(\frac{weight[kg]}{height[m]^2}\). Since our data gives the height in cm instead of meters, we have to divide this number by 100:
[1] 31.60321 23.01118 23.04002 21.27600 NAAs you can see there is a NA for the last case, because we have no weight information on this person. If you want to save the BMI for further analysis it makes sense to save it as a new variable in your tibble/data.frame. To create a new variable in an existing data.frame, your write its name behind a $ and use the assignment operator like this:
You can now see that you data see d has BMI as a variable:
# A tibble: 5 × 6
weight age id height eyecolor BMI
<dbl> <dbl> <chr> <dbl> <chr> <dbl>
1 85 34 1 164 blue 31.6
2 56 72 2 156 brown 23.0
3 73 33 3 178 green 23.0
4 76 45 4 189 brown 21.3
5 NA NA 6 169 blue NA You can also create variables using logical operators. Suppose you want to create an indicator variable blueEyes that takes the value 1 when a person has blue eyes and the value 0 else. First, you create a variable that takes the value 0 for everyone:
# A tibble: 5 × 7
weight age id height eyecolor BMI blueEyes
<dbl> <dbl> <chr> <dbl> <chr> <dbl> <dbl>
1 85 34 1 164 blue 31.6 0
2 56 72 2 156 brown 23.0 0
3 73 33 3 178 green 23.0 0
4 76 45 4 189 brown 21.3 0
5 NA NA 6 169 blue NA 0Now you have to set the variable 1 for every blue eyed person. You can create a vector telling you the blue eyed persons like this:
[1] TRUE FALSE FALSE FALSE TRUEIf you use this expression for subsetting the rows of the data.frame you get only the blue eyed persons:
# A tibble: 2 × 7
weight age id height eyecolor BMI blueEyes
<dbl> <dbl> <chr> <dbl> <chr> <dbl> <dbl>
1 85 34 1 164 blue 31.6 0
2 NA NA 6 169 blue NA 0You can now use this selection in combination with $blueEyes to set exactly those variable values to 1:
[1] 0 0# A tibble: 5 × 7
weight age id height eyecolor BMI blueEyes
<dbl> <dbl> <chr> <dbl> <chr> <dbl> <dbl>
1 85 34 1 164 blue 31.6 1
2 56 72 2 156 brown 23.0 0
3 73 33 3 178 green 23.0 0
4 76 45 4 189 brown 21.3 0
5 NA NA 6 169 blue NA 13.1.5 Computing summaries by group
One thing you will want to do quite often in statistics is to compute a certain statistic not for your whole sample but individually for certain subgroups. The steps needed for this are the following:
- group your data in subsets according to some factor, e.g. eye color
- apply the statistic to each subset
- combine the results in a suitable way
R has a huge number of solutions for this. Some of the most handy ones are part of the dplyr package, which you have already loaded as part of the tidyverse. Among others, this package introduces the so-called pipe operator %>% which is used to chain together multiple operations on the same data set.
The following code takes our data d and computes the the mean BMI and the median height for each eye color. Here is a breakdown of each line:
d %>%: Here the pipe operator (%>%) is used to pass the data framedinto the subsequent operations.group_by(eyecolor): Groups the data by the levels of the “eyecolor” variable, indicating that subsequent summary statistics will be calculated for each unique eyecolor group.summarise(meanBMI=mean(BMI, na.rm=T), medianHeight=median(height, na.rm=T)): This line creates summary statistics for each eyecolor group. It calculates the mean of theBMIvariable, assigning the result to a new variable calledmeanBMI. Similarly, it calculates the median of theheightvariable and assigns the result to a new variable calledmedianHeight. Thena.rm = Targument is used to exclude any missing values from the calculations.
d %>%
group_by(eyecolor) %>%
summarise(meanBMI = mean(BMI, na.rm = T),
medianHeight = median(height, na.rm = T)) # A tibble: 3 × 3
eyecolor meanBMI medianHeight
<chr> <dbl> <dbl>
1 blue 31.6 166.
2 brown 22.1 172.
3 green 23.0 178 Instead of generating a separate table for the summaries, an alternative approach is to integrate the computed values directly into the input data by substituting summarise() with mutate():
d %>%
group_by(eyecolor) %>%
mutate(meanBMI = mean(BMI, na.rm = T),
medianHeight = median(height, na.rm = T)) # A tibble: 5 × 9
# Groups: eyecolor [3]
weight age id height eyecolor BMI blueEyes meanBMI medianHeight
<dbl> <dbl> <chr> <dbl> <chr> <dbl> <dbl> <dbl> <dbl>
1 85 34 1 164 blue 31.6 1 31.6 166.
2 56 72 2 156 brown 23.0 0 22.1 172.
3 73 33 3 178 green 23.0 0 23.0 178
4 76 45 4 189 brown 21.3 0 22.1 172.
5 NA NA 6 169 blue NA 1 31.6 166.3.2 Diagnostic Tests
As you have learned in the lecture we can use ROC curves to assess the usefulness of one variable to predict the category of another variable. Our example data set from the first chapter for example contains the variable apache2_admission which is the Apache II score, a metric that assesses the risk of a patient’s death in ICU settings. We could try to predict the hospital death of our patients with this score. Let’s start by reading in the data set:
To import the necessary functions, we will use the package ROCit (Khan and Brandenburger 2024):
The function rocit() takes the arguments score (a numeric variable that is used for classification, i.e. the Apache II score) and class (the factor that defines the true class membership, i.e. whether the patient died or not) and returns an R object containing the diagnostic information which we will store in the variable rocObject:
We can plot the ROC curve by calling plot() on the object returned by rocit():
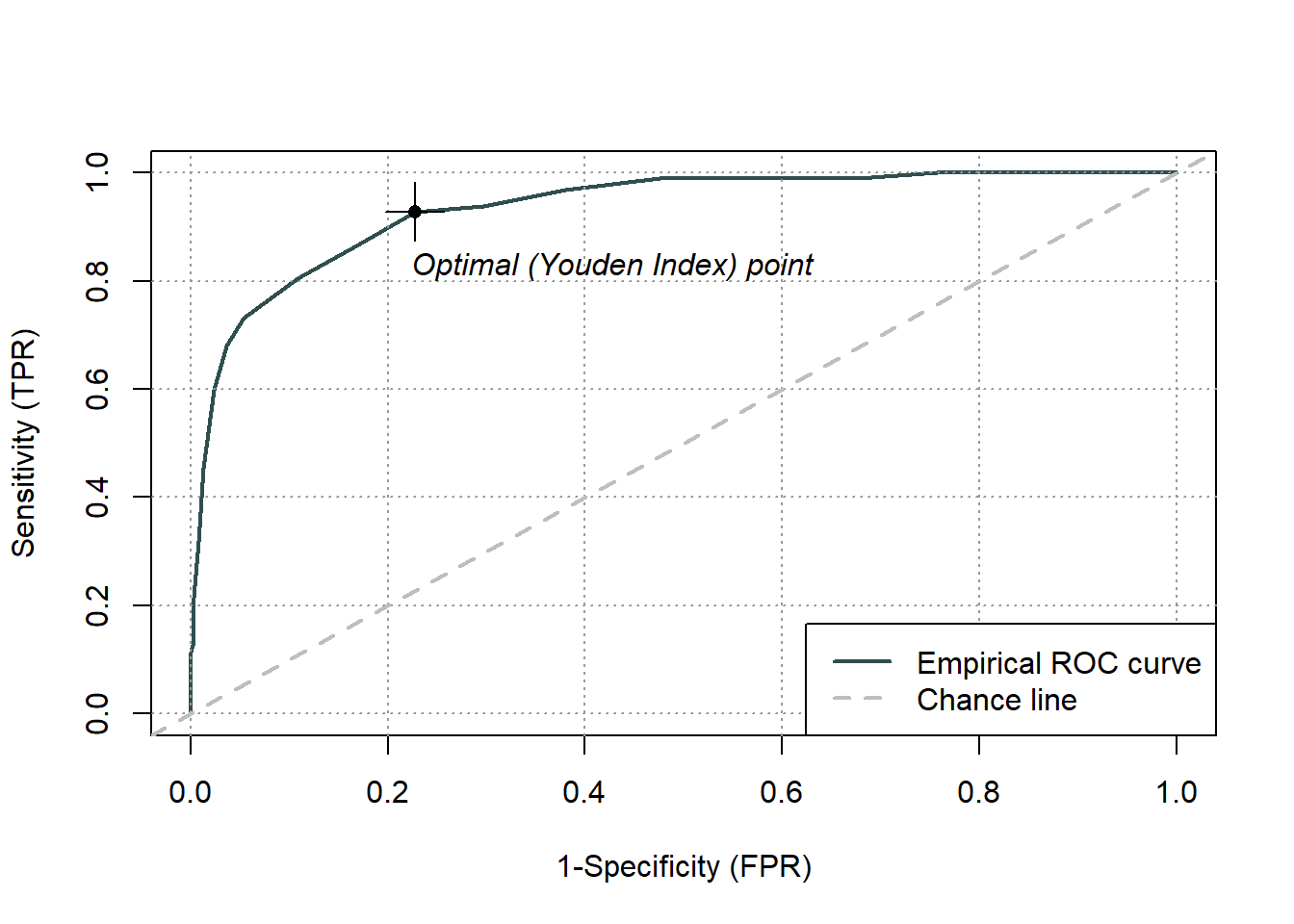
We can also extract a number of diagnostic properties for every cutoff with the function measureit(). This function takes the object returned by rocit() and the argument measure, a character string specifying which properties to compute. A list of the possible measures can be found on the help page for the function. Here we will use the sensitivity (SENS), the specificity (SPEC), the positive and negative predictive value (PPV and NPV) and the positive and negative diagnostic likelihood ratio (pDRL and nDLR). Because the result is quite large, we will save it under the name properties instead of just printing it to the console.
The object properties is a list. To get an overview over its elements, click on the little triangle in the blue circle next to properties in the environment window of RStudio.
You can have a closer look at its elements using the $:
[1] Inf 29 28 27 26 25 24 23 22 21 [1] 0.00000000 0.01030928 0.03092784 0.09278351 0.11340206 0.13402062
[7] 0.21649485 0.31958763 0.45360825 0.59793814The elements SENS and Cutoff are quite long numeric vectors, so the above code shows you two ways of printing only the first 10 elements of these vectors, [1:10] and head(, 10).
3.3 Comparing two samples
Comparing two samples allows us to assess if a particular variable (such as CRP value) varies between two groups (like treatment groups or different measurement points). The samples represent measurements of the variable in each group. Essentially, it is akin to examining whether a binary variable (like gender or time point) is linked to another variable (like CRP value). When the CRP values differ between an experimental treatment group and a control group, it indicates an association between the treatment and CRP.
3.3.1 Unpaired samples
Unpaired samples refer to individual data points collected from two separate groups or populations that are not matched or paired in any specific way. Observing a variable in two sets of different patients, for example, results in unpaired samples.
t-test
The t-test can be used to test if the means of normally distributed metric variables differ significantly. You can either test the sample mean against a prespecified mean or you can test whether the means of two samples differ significantly.
For a one sample t-test you use the function t.test() which takes a numeric vector and mu, the mean you want to test your sample mean against:
One Sample t-test
data: data$age
t = 17.568, df = 490, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 50
95 percent confidence interval:
58.44025 60.56586
sample estimates:
mean of x
59.50305 In the output, you find the value of the test statistic (i.e. the t value), its degrees of freedom and the corresponding p-value in the first row. If the p value is very small it is displayed in scientific notation, e.g. p-value < 2.2e-16 which means \(p < 2.2 \times 10^{-16}\).
In the row below you get the alternative hypothesis in words and below that the confidence interval for the sample mean.
You can judge the significance of the result by checking whether your p-value undercuts the significance level (e.g. 0.05) or by checking whether the confidence interval includes mu, i.e. 50.
To report the results of a t-test, you provide the t-value with its degrees of freedom and the p-value, typically stating it as below a certain margin, such as 0.001; for example, the mean age significantly differs from 50 with t(490)=17.568, p<0.001. Additionally, including the estimated mean and its confidence interval (in this case 59.50 [58.44 ; 60.57]) allows readers to assess both the statistical significance and clinical relevance of the result.
For the two-sample t-test, you have two methods to input your samples into the function. Here, we will demonstrate one approach that only works for unpaired samples, reserving the other for the paired t-test example. In this first method, you provide the function with the variable containing the measured values and a grouping variable denoting which values correspond to each group, separated by a ~.
For instance, to compare the body weight at admission between men and women, you would input data$weight_admission ~ data$gender, evaluating of the relationship between weight_admission and the dichotomous variable gender.
#test whether admission weight differs between men and women
t.test(data$weight_admission ~ data$gender)
Welch Two Sample t-test
data: data$weight_admission by data$gender
t = -25.211, df = 484.29, p-value < 2.2e-16
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
-15.45045 -13.21625
sample estimates:
mean in group female mean in group male
66.46748 80.80083 In this case, R defaults to conducting the Welch test, which accommodates variations in variances between the two samples. However, if you are certain that the variances are equal, you can specify var.equal=TRUE to perform the standard t-test.
With the alternative hypothesis and confidence interval now focused on the mean difference between men and women, a significant outcome is indicated by a confidence interval excluding 0 and a p-value < 0.05. Consequently, our results reveal a significant difference in weight between men and women in our sample, evidenced by t(484.29) = -25.211, p<0.001.
Wilcoxon-Mann-Whitney test
The Wilcoxon-Mann-Whitney test is a non-parametric substitute for the t-test, used when your two samples are metric or ordinal with multiple potential values. Since it does not rely on distribution assumptions, the alternative hypothesis does not specifically concern mean differences but rather a shift in location between the two samples. The arguments of the wilcox.test() function operate similarly to those of the t.test() function:
Wilcoxon rank sum test with continuity correction
data: data$apache2_admission by data$gender
W = 19820, p-value = 1.582e-10
alternative hypothesis: true location shift is not equal to 0The results tell us that the Apache II score differs significantly between men and women with p<0.001.
Chi-square-test
The Chi-square test examines whether there is an association between two dichotomous variables, essentially probing whether the probability distribution of one variable varies across groups defined by the other variable. For instance, we can evaluate if there is a difference in hospital deaths between experimental and control treatment by providing both dichotomous variables to the chisq.test() function:
Pearson's Chi-squared test with Yates' continuity correction
data: data$hospital_death and data$treatment
X-squared = 15.211, df = 1, p-value = 9.615e-05As you can see, there is a significant difference in the probability of hospital death between patients receiving the experimental vs. the control medication with p<0.001.
3.3.2 Paired samples
Paired samples are data collected from the same group or subjects under two different conditions or times, where each data point in one condition is linked or matched with a specific data point in the other condition. In our example dataset, CRP values measured both at admission and discharge, or weights measured at admission and discharge, are considered paired because they originate from the same patients.
T-Test
For paired samples of metric, symmetric, and normally distributed variables, the paired t-test can be employed. As mentioned earlier, here we will introduce an alternative method for specifying the data. If your observations are stored in two distinct vectors (unlike the unpaired t-test example where all weight observations were stored in one vector, divisible by gender), you can input these two vectors separated by a comma into the t-test function. If the samples are paired, you set the argument paired=TRUE to get a paired t-test:
Paired t-test
data: data$weight_admission and data$weight_discharge
t = -0.72487, df = 383, p-value = 0.469
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-0.4253854 0.1962187
sample estimates:
mean difference
-0.1145833 The result indicates that there is no significant difference between the weight at admission and the weight at discharge with t(383) = -0.72487, p = 0.469
Wilcoxon test
If your samples are metric and symmetric but not normally distributed, you can use the Wilcoxon-test. You have already encountered the wilcox.test() function before, now we just have to set the argument paired = TRUE:
Wilcoxon signed rank test with continuity correction
data: data$crp_admission and data$crp_discharge
V = 73299, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0The output tells us that there is a significant difference between the CRP values at admission and at discharge with p<0.001.
Sign-Test
The Sign-test is suitable for ordinal data with multiple possible values, assessing whether the median of paired differences between two samples equals 0 (for two-sided tests) or is greater/less than 0 (for one-sided tests). If the median of differences is greater than 0, it implies that the first variable is predominantly greater across the majority of value pairs; conversely, if the median is less than 0, it indicates the second variable is predominantly greater.
To do this test in R, we can use the SIGN.test() function from the BSDA package (Arnholt and Evans 2023):
Dependent-samples Sign-Test
data: data$apache2_admission and data$apache2_discharge
S = 378, p-value < 2.2e-16
alternative hypothesis: true median difference is greater than 0
95 percent confidence interval:
7 Inf
sample estimates:
median of x-y
8
Achieved and Interpolated Confidence Intervals:
Conf.Level L.E.pt U.E.pt
Lower Achieved CI 0.9442 7 Inf
Interpolated CI 0.9500 7 Inf
Upper Achieved CI 0.9548 7 InfThe p-value below 0.05 indicates that a significant majority of patients has a higher Apache II value at admission than at discharge.
Mc Nemar test
The Mc Nemar tests whether two dichotomous variables occur with different frequencies (i.e. different probabilities for the “yes-event”). It can be used on paired samples, e.g. where a variable have been measured twice on the same patient like organ dysfunction at admission (organ_dysfunction_admission) and organ dysfunction at discharge (organ_dysfunction_discharge):
McNemar's Chi-squared test with continuity correction
data: data$organ_dysfunction_admission and data$organ_dysfunction_discharge
McNemar's chi-squared = 204.54, df = 1, p-value < 2.2e-16As we can see there is a significant difference in the distribution of the organ dysfunction status between admission and discharge from ICU with \(\chi^2\)(1) = 204.54, p<0.001
3.4 Troubleshooting
Error in xy: could not find function “xy” where xy stands for the function in your error message. You probably forgot to load the package containing the function or you misspelled the function. If you are unsure which package it belongs to, consider googling the function.
Error in library(xy) : there is no package called ‘xy’ where xy stands for the package name in your error message. You probably forgot to install the package before loading it. Try
install.packages("xy"). If the installation fails, check if you are connected to the internet and have sufficient rights on you computer to install software.