Chapter 7 Lab 5 - 25/10/2022

In this lecture we will learn two other dplyr verbs and the ggplot2 library which is used to produce very nice plots. The final part is dedicated to the import of data from an external csv file.

We will use the diamods data from the tidyverse package:

library(tidyverse)
head(diamonds)
## # A tibble: 6 × 10
##   carat cut       color clarity depth table price     x     y     z
##   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>
## 1  0.23 Ideal     E     SI2      61.5    55   326  3.95  3.98  2.43
## 2  0.21 Premium   E     SI1      59.8    61   326  3.89  3.84  2.31
## 3  0.23 Good      E     VS1      56.9    65   327  4.05  4.07  2.31
## 4  0.29 Premium   I     VS2      62.4    58   334  4.2   4.23  2.63
## 5  0.31 Good      J     SI2      63.3    58   335  4.34  4.35  2.75
## 6  0.24 Very Good J     VVS2     62.8    57   336  3.94  3.96  2.48

7.1 An alternative approach for getting a frequency distribution

In the previous lab we derived the absolute and percentage distribution by using the function n() combined with group_by:

diamonds %>% 
  group_by(cut) %>% 
  summarise(AbsFreq = n(), #absolute frequencies
            Perc = AbsFreq/nrow(diamonds)*100) #%
## # A tibble: 5 × 3
##   cut       AbsFreq  Perc
##   <ord>       <int> <dbl>
## 1 Fair         1610  2.98
## 2 Good         4906  9.10
## 3 Very Good   12082 22.4 
## 4 Premium     13791 25.6 
## 5 Ideal       21551 40.0

A shorter alternative for computing the frequency table is given by the count function which count the unique values of one or more variables. Basically, df %>% count(a, b) is equivalent to df %>% group_by(a, b) %>% summarise(n = n()). Here below we have an example:

diamonds %>% 
  count(cut)
## # A tibble: 5 × 2
##   cut           n
##   <ord>     <int>
## 1 Fair       1610
## 2 Good       4906
## 3 Very Good 12082
## 4 Premium   13791
## 5 Ideal     21551

7.2 Verb 5: mutate

The verb mutate can be used to create new column in the data frame. For example, let’s create a new column containing the price per unit defined previously. Moreover, we want this variable to be saved in the data frame (for this reason we create a new object named diamonds which substitutes its previous version):

diamonds = diamonds %>% 
  mutate(priceunit = price/carat)
dim(diamonds)
## [1] 53940    11

We now want to create a new categorical variables with two categories: “Yes” if the price is < 1000$, “No” otherwise. For doing this we will make use of the ifelse function, already introduced in Section 5.5. We will call the new column as pricecat and will save the new data frame (with one more column) in a new object named newdiamonds:

newdiamonds = diamonds %>% 
  mutate(pricecat = ifelse(price < 1000, "Yes", "No"))

To derive the frequency distribution of pricecat we proceed as described above, computing also percentages by means of mutate:

newdiamonds %>% 
  count(pricecat) %>% 
  #summarise(perc=n/nrow(newdiamonds)*100)
  mutate(perc=n/nrow(newdiamonds)*100)
## # A tibble: 2 × 3
##   pricecat     n  perc
##   <chr>    <int> <dbl>
## 1 No       39441  73.1
## 2 Yes      14499  26.9

7.3 Verb 6: arrange

The verb arrange can be used to sort observations with respect to the values of a given variable. For example, we can sort diamonds according to price (by default the ascending order is adopted):

diamonds %>% 
  arrange(price) %>% 
  tail
## # A tibble: 6 × 11
##   carat cut       color clarity depth table price     x     y     z priceunit
##   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>     <dbl>
## 1  2.29 Premium   I     SI1      61.8    59 18797  8.52  8.45  5.24     8208.
## 2  2    Very Good H     SI1      62.8    57 18803  7.95  8     5.01     9402.
## 3  2.07 Ideal     G     SI2      62.5    55 18804  8.2   8.13  5.11     9084.
## 4  1.51 Ideal     G     IF       61.7    55 18806  7.37  7.41  4.56    12454.
## 5  2    Very Good G     SI1      63.5    56 18818  7.9   7.97  5.04     9409 
## 6  2.29 Premium   I     VS2      60.8    60 18823  8.5   8.47  5.16     8220.

With the function tail we have a preview of the 6 bottom lines which contains, in this case, the diamonds with the highest price.

If we need to use a descending ordering we will use the - inside arrange:

diamonds %>% 
  arrange(- price)
## # A tibble: 53,940 × 11
##    carat cut       color clarity depth table price     x     y     z priceunit
##    <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>     <dbl>
##  1  2.29 Premium   I     VS2      60.8    60 18823  8.5   8.47  5.16     8220.
##  2  2    Very Good G     SI1      63.5    56 18818  7.9   7.97  5.04     9409 
##  3  1.51 Ideal     G     IF       61.7    55 18806  7.37  7.41  4.56    12454.
##  4  2.07 Ideal     G     SI2      62.5    55 18804  8.2   8.13  5.11     9084.
##  5  2    Very Good H     SI1      62.8    57 18803  7.95  8     5.01     9402.
##  6  2.29 Premium   I     SI1      61.8    59 18797  8.52  8.45  5.24     8208.
##  7  2.04 Premium   H     SI1      58.1    60 18795  8.37  8.28  4.84     9213.
##  8  2    Premium   I     VS1      60.8    59 18795  8.13  8.02  4.91     9398.
##  9  1.71 Premium   F     VS2      62.3    59 18791  7.57  7.53  4.7     10989.
## 10  2.15 Ideal     G     SI2      62.6    54 18791  8.29  8.35  5.21     8740 
## # … with 53,930 more rows

Let’s now use the arrange function in order to sort the categories of a factor (cut) according to the corresponding frequencies:

diamonds %>% 
  group_by(cut) %>% 
  summarise(freq = n()) %>% 
  arrange(desc(freq))
## # A tibble: 5 × 2
##   cut        freq
##   <ord>     <int>
## 1 Ideal     21551
## 2 Premium   13791
## 3 Very Good 12082
## 4 Good       4906
## 5 Fair       1610

It can be also useful to visualize a given number or proportion observations with the highest/lowest values of a given variable. The following code for example extract first the 10 observations with the highest values of carat (using slice_max) and among them the 50% of the observations with the lowest price (with slice_min):

diamonds %>% 
  slice_max(carat, n=10) %>% 
  slice_min(price, prop=0.5) 
## # A tibble: 5 × 11
##   carat cut       color clarity depth table price     x     y     z priceunit
##   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>     <dbl>
## 1  3.65 Fair      H     I1       67.1    53 11668  9.53  9.48  6.38     3197.
## 2  3.5  Ideal     H     I1       62.8    57 12587  9.65  9.59  6.03     3596.
## 3  4.01 Premium   I     I1       61      61 15223 10.1  10.1   6.17     3796.
## 4  4.01 Premium   J     I1       62.5    62 15223 10.0   9.94  6.24     3796.
## 5  4    Very Good I     I1       63.3    58 15984 10.0   9.94  6.31     3996

7.4 The ggplot2 library

The ggplot2 is part of the tidyverse collection of packages. The grammar of graphics plot (ggplot) is an alternative to standard R functions for plotting; see here for the ggplot2 website. In Figure 7.1-7.3 we have some examples of plot (simple scatterplot, scatterplot with legend and boxplots) produced using standard R code and the ggplot2 library.

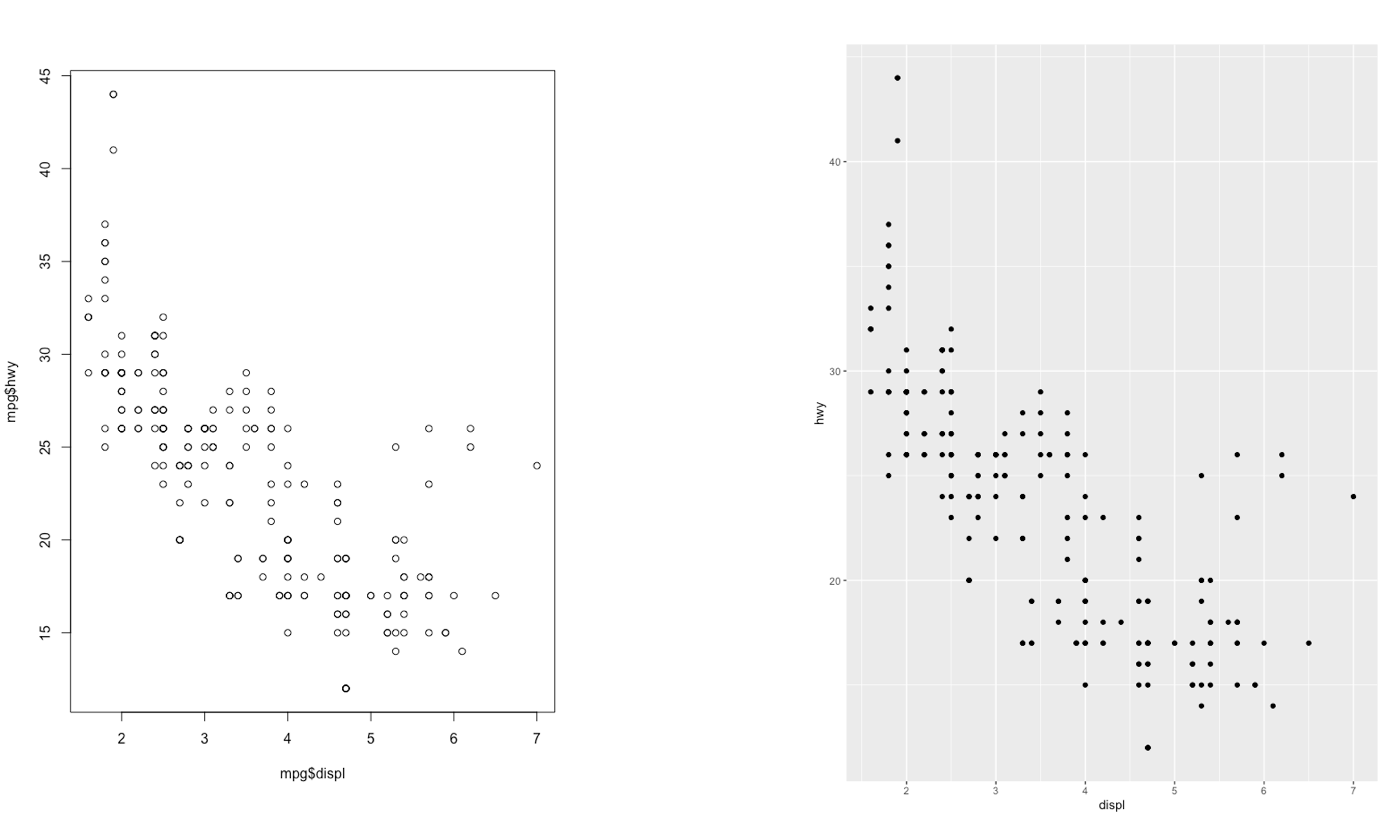
Comparison between standard and ggplot2 plots

Figure 7.1: Comparison between standard and ggplot2 plots

Comparison between standard and ggplot2 plots

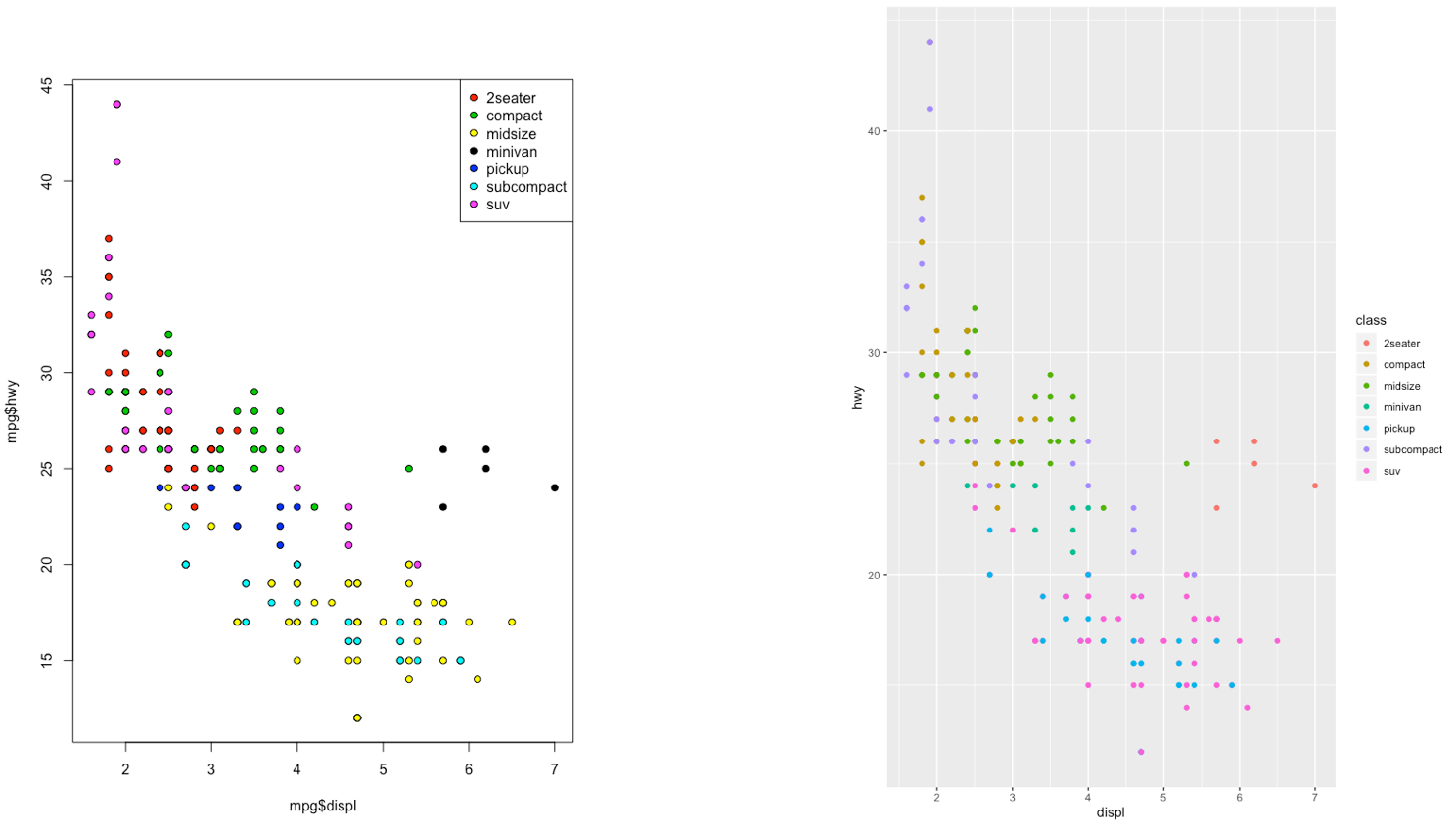
Figure 7.2: Comparison between standard and ggplot2 plots

Comparison between standard and ggplot2 plots

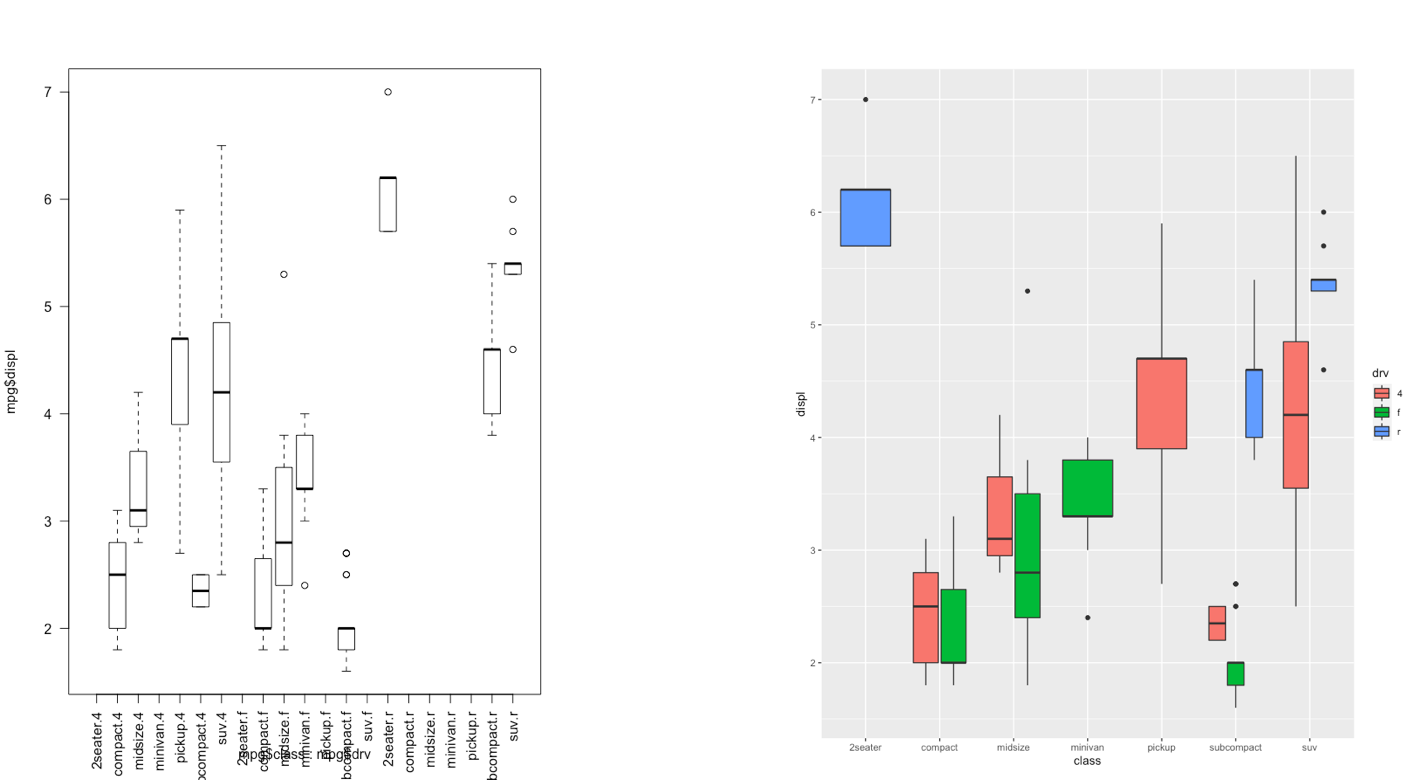
Figure 7.3: Comparison between standard and ggplot2 plots

With ggplot2 a plot is defined by several layers, as shown in Figure 7.4. The first layer specifies the coordinate system, then we can have several geometries each with an aesthetics specification.

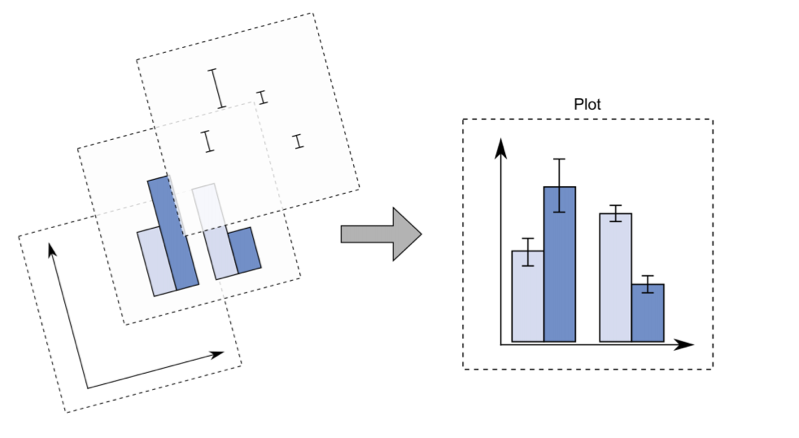
The layer structure of the `ggplot2` plot

Figure 7.4: The layer structure of the ggplot2 plot

I suggest to download from here the ggplot2 cheat sheet.

7.5 Data subsetting and the ggplot function

Instead of working with the entire diamonds data set, as done in Lecture 4, we will create a smaller data set by sampling randomly 1% of the diamonds by means of the function slice_sample. As this is a random procedure we set, as usual, the seed in order to have a reproducible outcome. The new (smaller) data set will be called mydiamonds:

library(tidyverse)
set.seed(4)
mydiamonds = slice_sample(diamonds, prop=0.01)
glimpse(mydiamonds)
## Rows: 539
## Columns: 11
## $ carat     <dbl> 0.72, 1.52, 0.32, 1.10, 1.34, 0.31, 0.26, 0.70, 0.36, 0.37, …
## $ cut       <ord> Ideal, Good, Premium, Premium, Ideal, Very Good, Ideal, Prem…
## $ color     <ord> E, J, G, J, H, G, I, G, E, D, I, H, E, D, G, I, G, G, E, H, …
## $ clarity   <ord> VS2, VS2, SI1, VS2, SI1, VVS1, VS2, SI1, VS1, SI1, VS1, VS2,…
## $ depth     <dbl> 62.8, 63.3, 61.0, 61.2, 62.4, 63.0, 62.0, 61.8, 60.9, 62.7, …
## $ table     <dbl> 57, 56, 61, 57, 54, 56, 56, 59, 57, 58, 60, 61, 59, 56, 54, …
## $ price     <int> 2835, 7370, 612, 3696, 7659, 710, 385, 2184, 782, 874, 6279,…
## $ x         <dbl> 5.71, 7.27, 4.41, 6.66, 7.05, 4.26, 4.13, 5.68, 4.60, 4.58, …
## $ y         <dbl> 5.73, 7.33, 4.38, 6.61, 7.08, 4.28, 4.09, 5.59, 4.63, 4.55, …
## $ z         <dbl> 3.59, 4.62, 2.68, 4.06, 4.41, 2.69, 2.55, 3.48, 2.81, 2.86, …
## $ priceunit <dbl> 3937.500, 4848.684, 1912.500, 3360.000, 5715.672, 2290.323, …

The most important function of the ggplot2 library is the ggplot function. All ggplot plots begin with a call to ggplot supplying the data:

ggplot(data = …) +
  geom_function(mapping = aes(…))

where geom_function is a generic function for a geometry layer; see here for the list of all the available geometries.

For starting a new empty plot we can proceed by using one of the following codes:

ggplot(data=mydiamonds)

ggplot(mydiamonds) #the argument name can be omitted

mydiamonds %>% 
  ggplot() #using the pipe

To add components and layers to the empty plot we will use the + symbol.

7.5.1 Scatterplot

We begin with a scatterplot displaying price on the y-axis and carat on the x-axis; the necessary geometry is implemented with geom_point:

mydiamonds %>% 
  ggplot() +
  geom_point(mapping = aes(x=carat,y=price))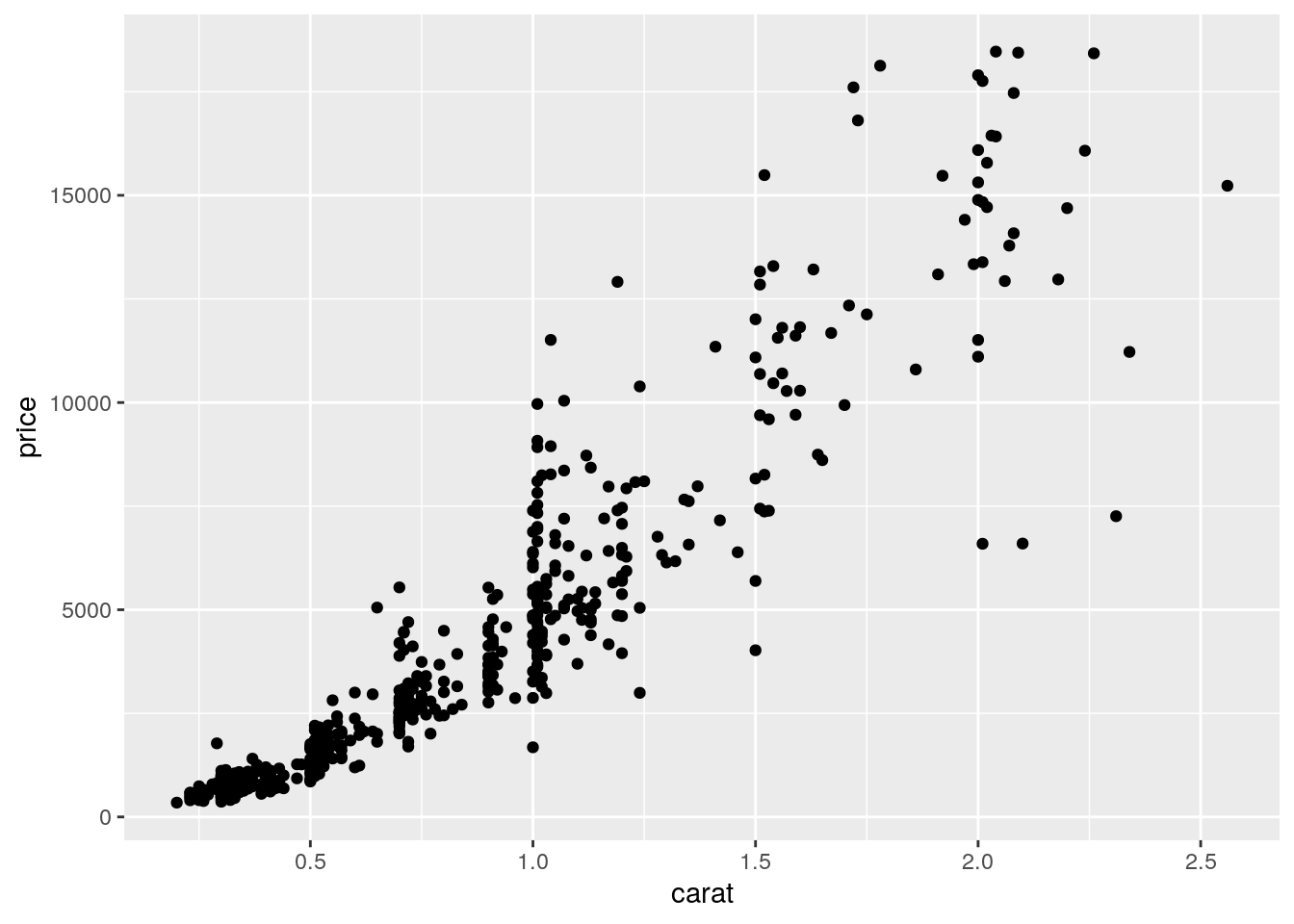

The argument mapping specifies the set of aesthetic mappings, created by aes, which describe the visual characteristics that represent the data, e.g. position, size, color, shape, transparency, fill, etc. Remember that the argument name can always be omitted. From the scatterplot we observe that a positive non linear relationship exists between carat and price.

It is also possible to specify a color for all the points as for example red:

mydiamonds %>% 
  ggplot() +
  geom_point(aes(x=carat,y=price),
             col="red")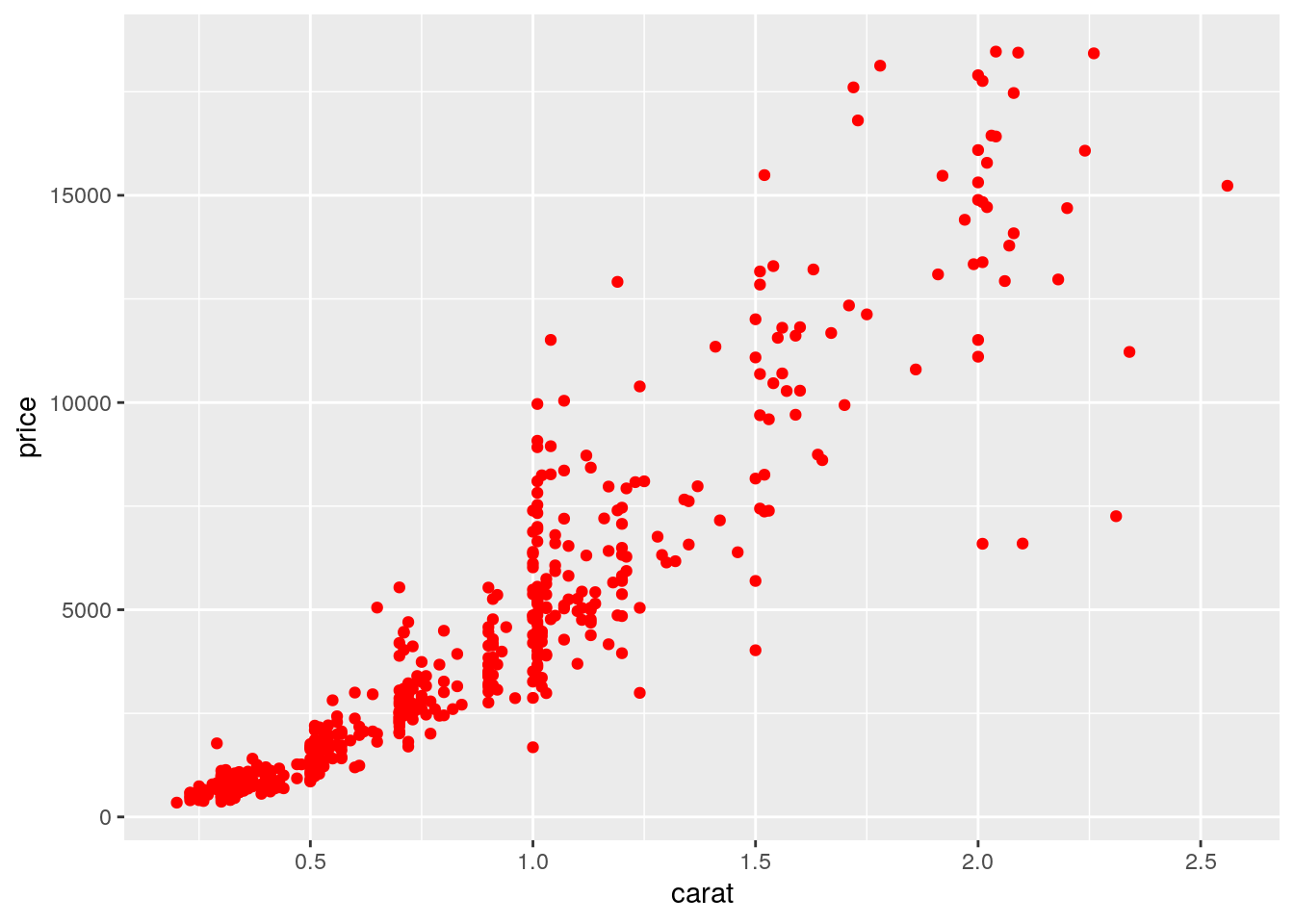

When the color is the same for all the points it is placed outside of aes() and is specified by quotes. A different case is when we have a different color for each point according, for example, to the corresponding category of the variable cut. In this case the color specification is included inside aes():

mydiamonds %>% 
  ggplot() +
  geom_point(aes(x=carat,y=price,color=cut))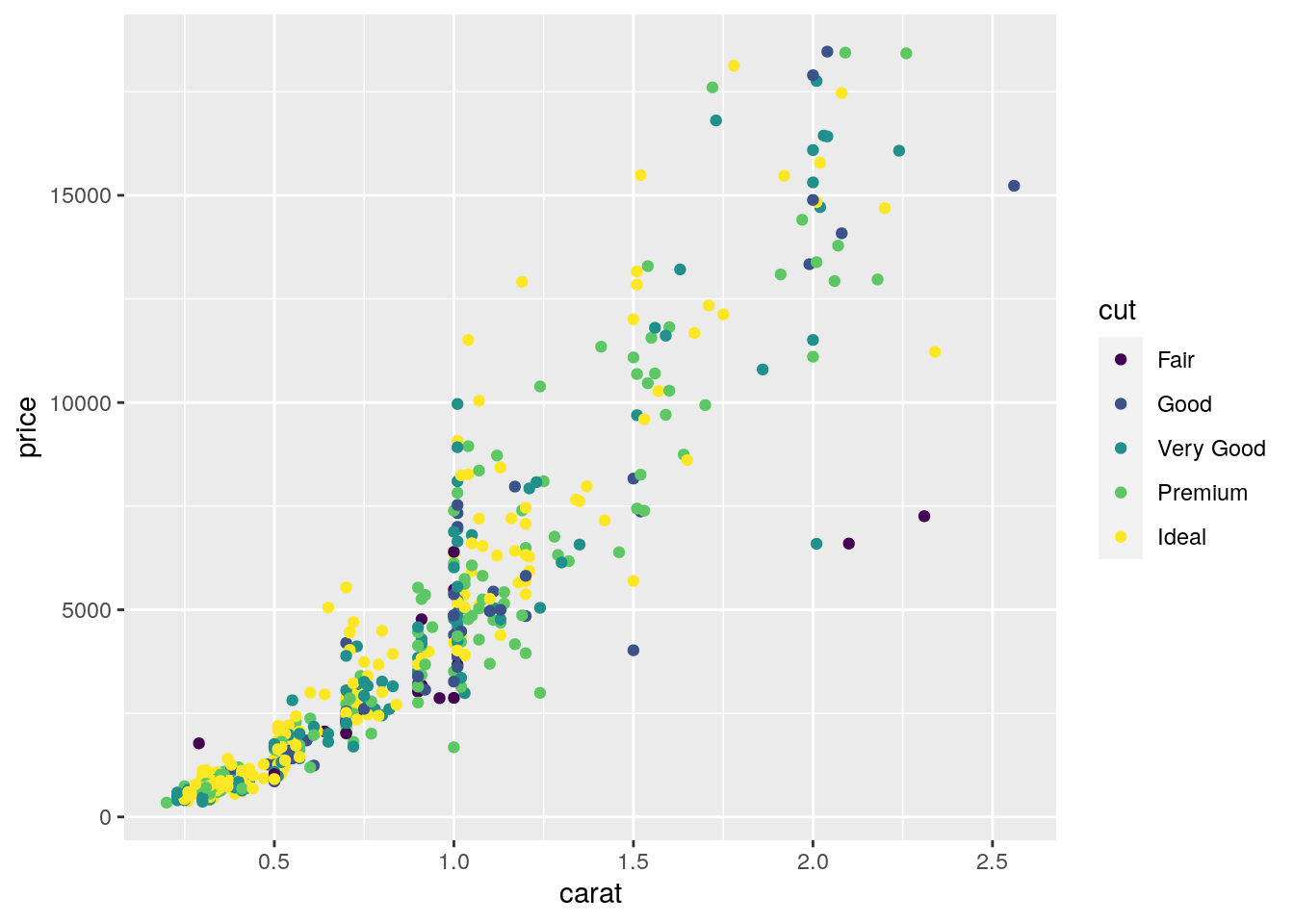

Note that automatically a legend is added that explains which level corresponds to each color. From the plot we do not observe a clear clustering of the diamonds according to their quality.

There is also the possibility to set the color according to a condition, e.g. cut == "Premium":

mydiamonds %>% 
  ggplot() +
  geom_point(aes(x=carat, y=price,
                 color = (cut=="Premium")))+
  labs(color = "Premium cut")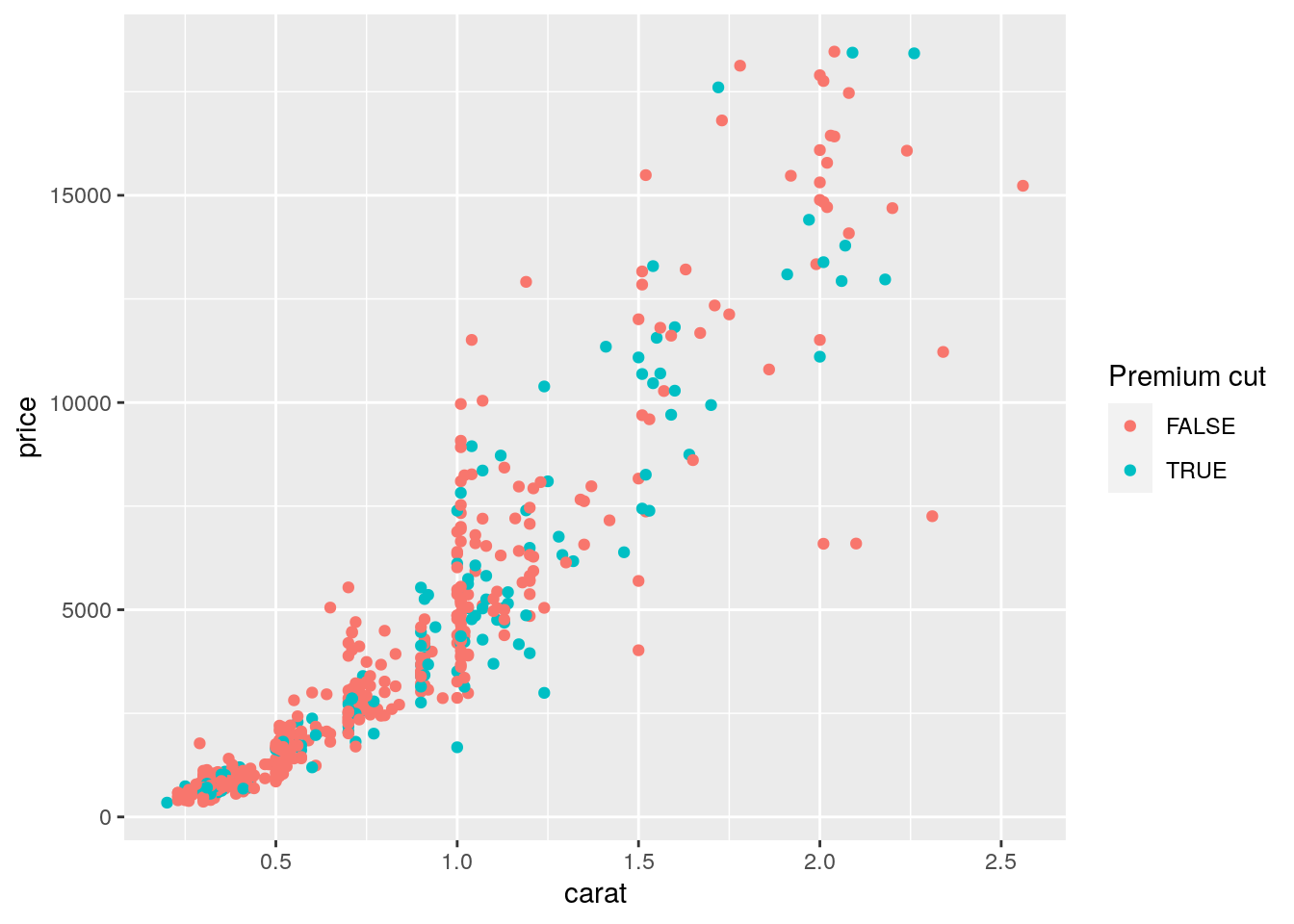

In this case the red color is used when the condition is false, and the blue (kind of) color when it is true.

It is also possible to set a different shape - instead of points - according to the categories of cut:

mydiamonds %>% 
  ggplot() +
  geom_point(aes(x=carat,y=price,shape=cut),
             color="blue")
## Warning: Using shapes for an ordinal variable is not advised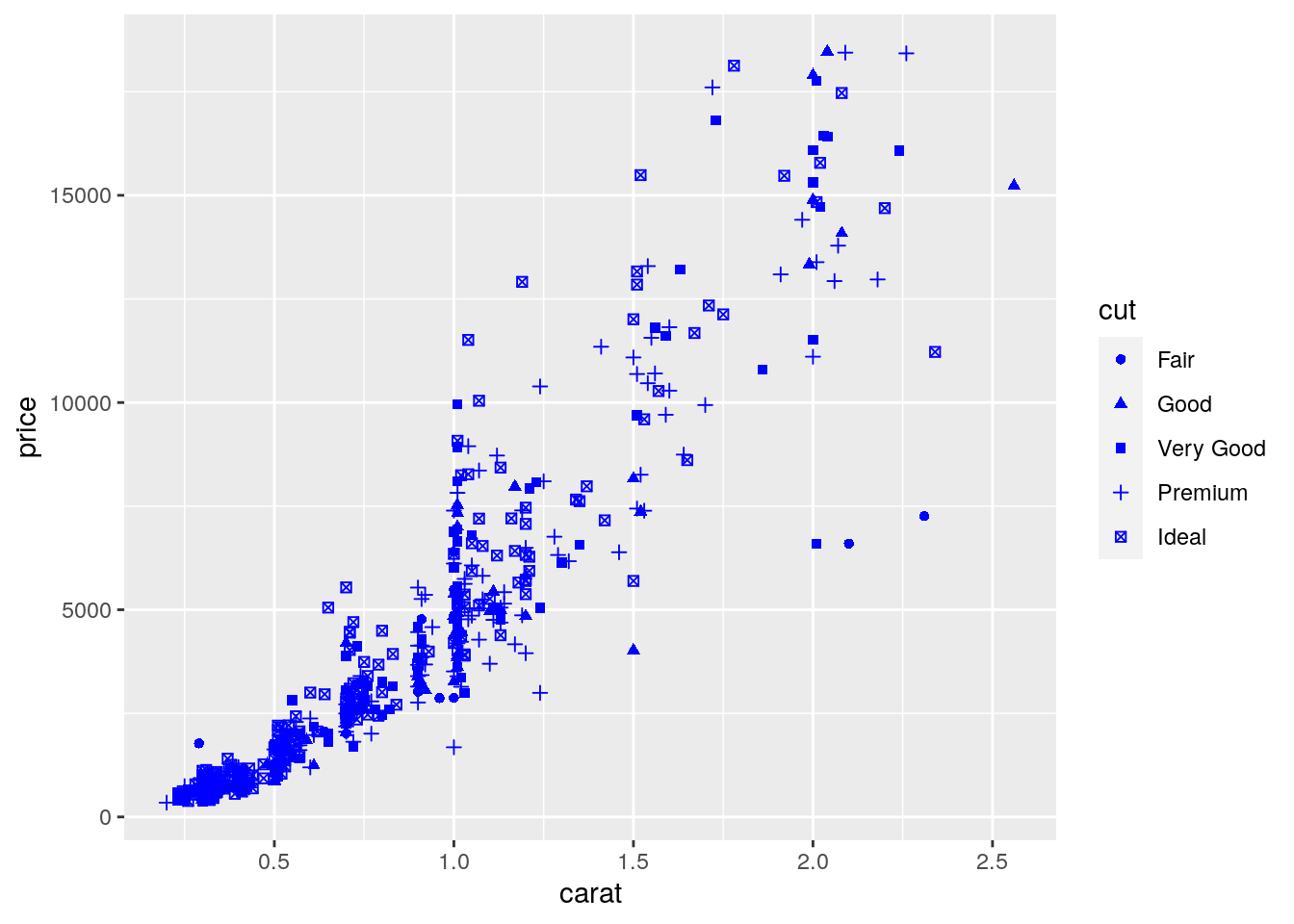

And it is also possible to use different sizes for each point according for example to the categories of clarity:

mydiamonds %>% 
  ggplot() +
  geom_point(aes(x=carat, y=price, col=cut, size=clarity))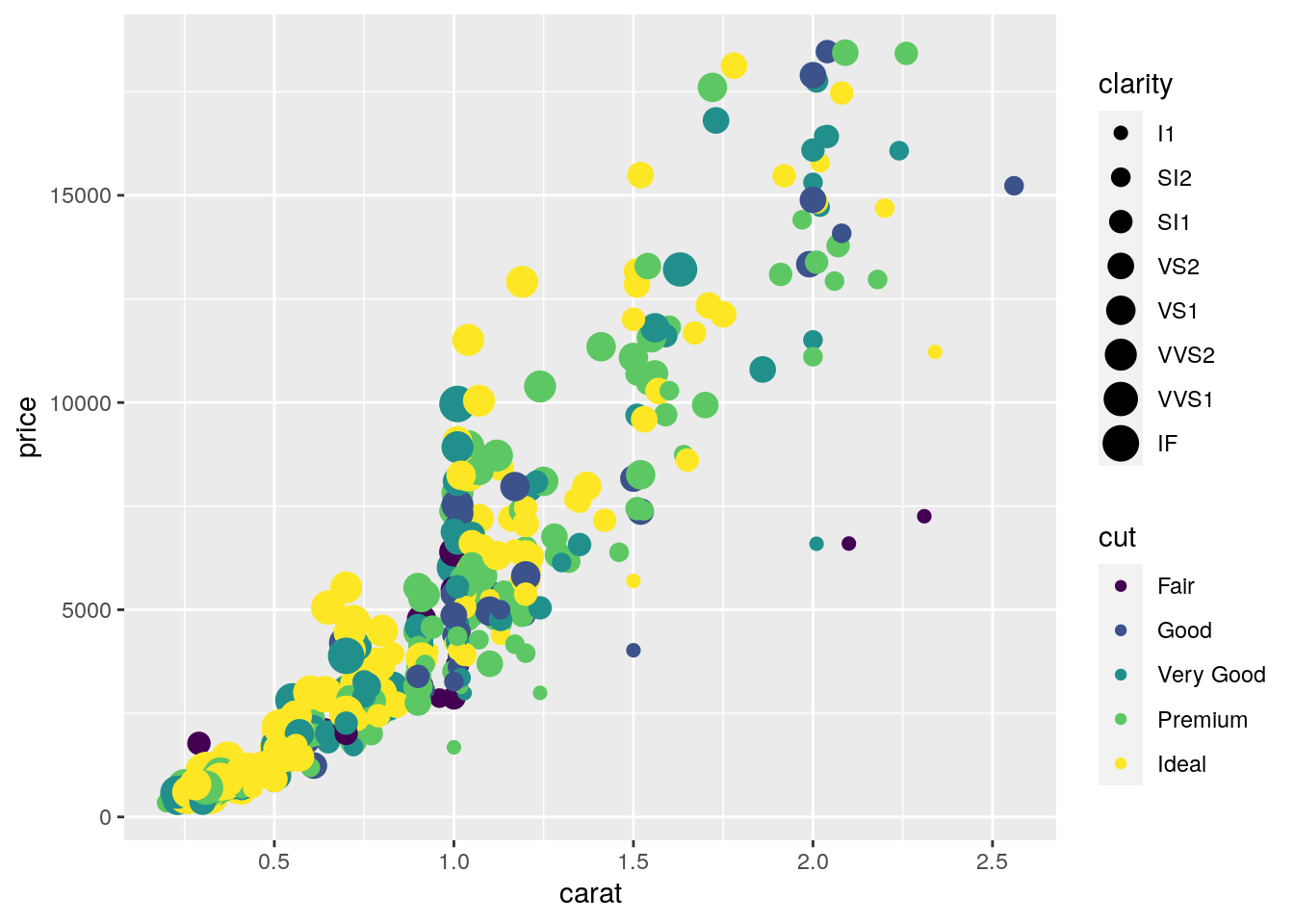

Finally, an alternative for considering the distribution of carat and price conditionally on cut is to produce 5 separate scatterplots according to the 5 categories of cut. In this case we use the facet which defines how data are split among panels. The default facet puts all the data in a single panel, while facet_wrap() and facet_grid() allow you to specify different types of small multiple plot.

mydiamonds %>% 
  ggplot() +
  geom_point(aes(x=carat,y=price)) +
  geom_smooth(aes(x=carat,y=price)) +
  facet_wrap(~cut) 
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'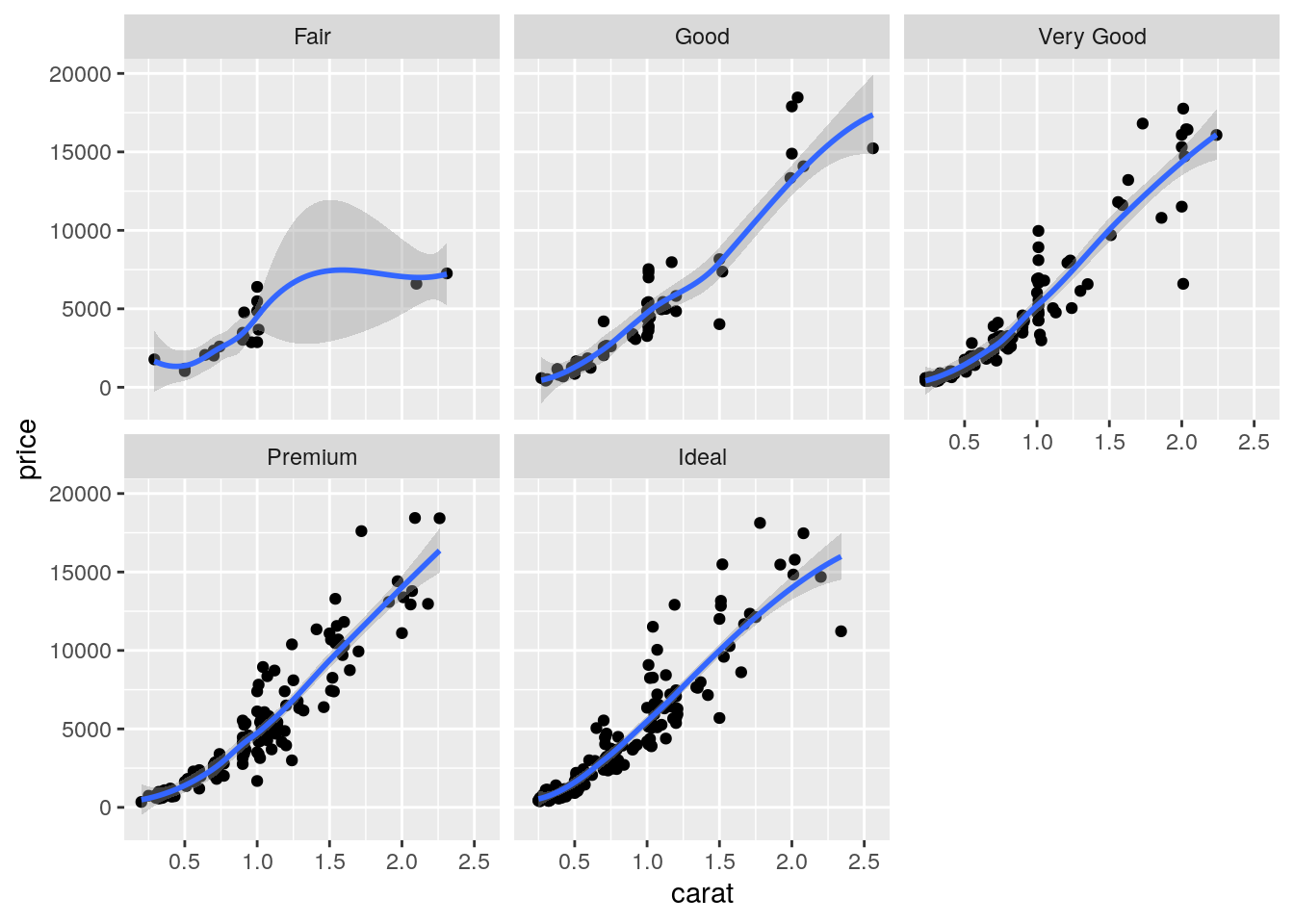

Note that in all the facets reported in the previous plot a new geometry (a new layer) has been included by means of geom_smooth, which adds in the plot a smooth line that can be ease the interpretation of the pattern in the plots. If we want to have a linear line we can use the input method="lm". Moreover, note that the two layers share the same aes() specification which can thus be provided once in the main ggplot() function:

mydiamonds %>% 
  ggplot(aes(x=carat,y=price)) +
  geom_point() +
  geom_smooth(method="lm") +
  facet_wrap(~cut) 
## `geom_smooth()` using formula 'y ~ x'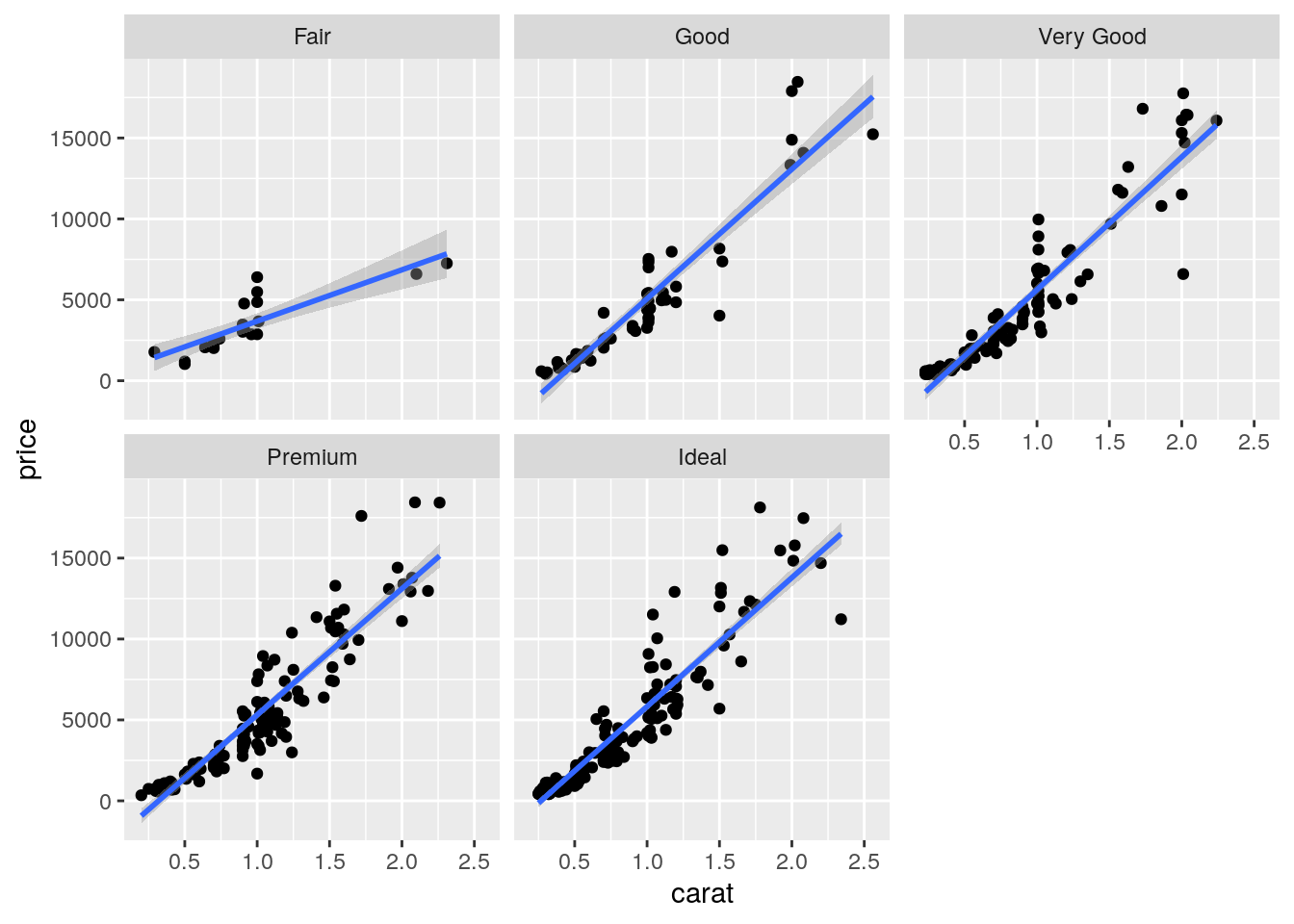

7.5.2 Boxplot

The boxplot can be used to study the distribution of a quantitative variable (e.g. price) conditioning on the categories of a factor (e.g. cut). It can be obtained by using the geom_boxplot geometry, where x is given by the qualitative variable (factor):

mydiamonds %>% 
  ggplot() +
  geom_boxplot(aes(x=cut,y=price))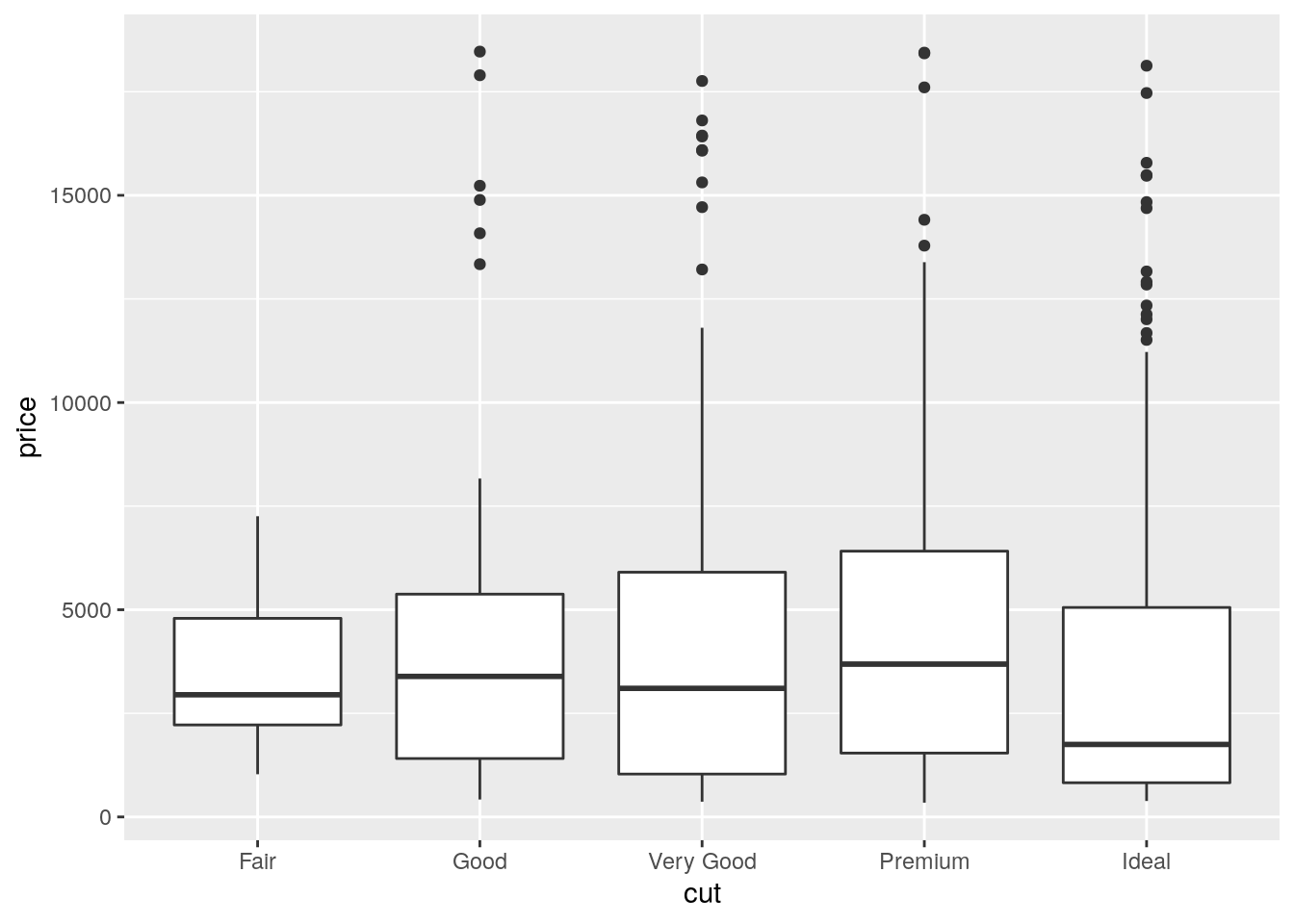

The quality category with highest (lowest) median price is Premium (Ideal). Fair quality diamonds are characterized by less variability in terms of price and are not characterized by extreme price values as happened for the other categories.

It is also possible to choose a different fill color and contour color for all the boxes by using fill and color:

mydiamonds %>% 
  ggplot() +
  geom_boxplot(aes(x=cut,y=price),
               fill="orange",color="brown")

In the previous plot all the boxes are characterized by the same fill and contour color. If we instead interested in using different fill colors according to a variable (e.g.color) we have to specify the aesthetics with aes():

mydiamonds %>% 
  ggplot() +
  geom_boxplot(aes(x=cut,y=price,fill=color),
               col="brown")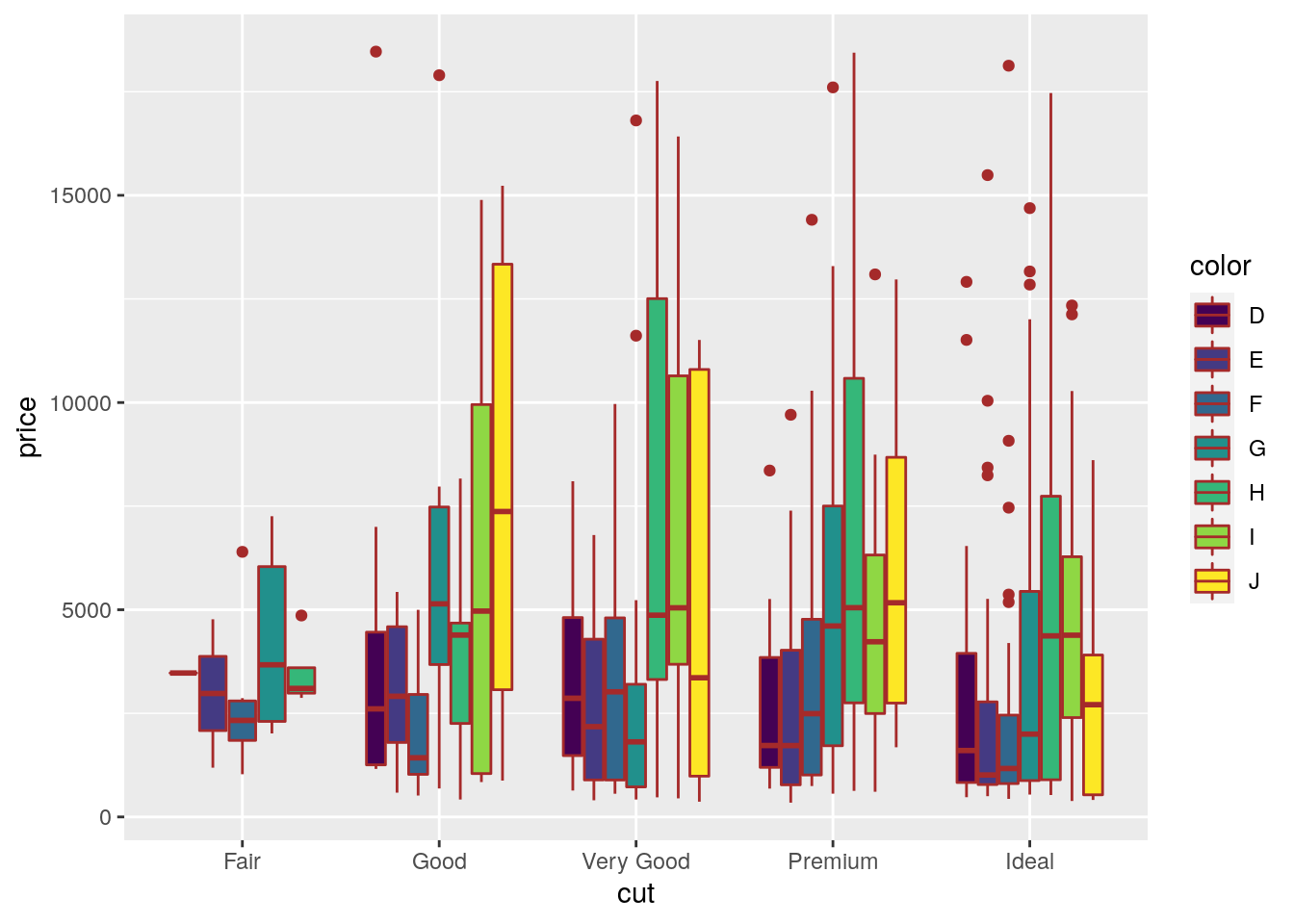

In this case for each cut category we have several boxplots (for the price distribution) according to the color categories.

7.5.3 Histogram and density plot

When the aim is the analysis of the distribution of a continuos variable like price an histogram can be used. This is implemented by using the geom_histogram geometry:

mydiamonds %>% 
  ggplot() +
  geom_histogram(aes(x=price),
                 fill="lightblue",color="black")
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.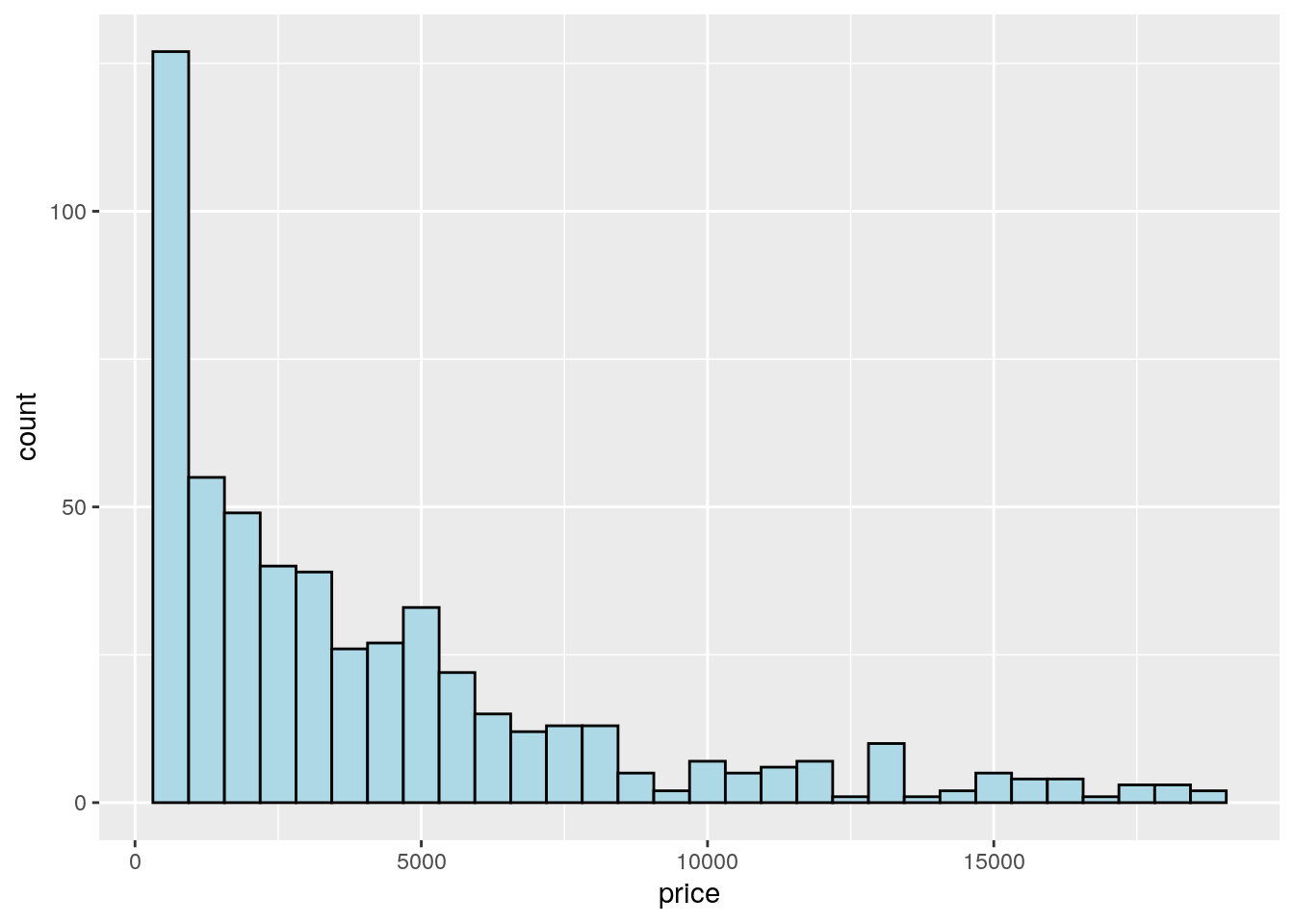

Note that in this case we need to specify only the x variable, while the y is computed automatically by ggplot and corresponds to the count variable (i.e. how many observations for each class of price values). This is given by the fact that every geometry has a default stat specification. For the histogram the default computation is stat_bin which uses 30 bins and computes the following variables:

  • count, the number of observations in each bin;
  • density, the density of observations in each bin (percentage of total / bar width);
  • x, the centre of the bin.

The histogram is a fairly crude estimator of the variable distribution. As an alternative it is possible to use the (non parametric) Kernel Density Estimation (see here) implemented in ggplot by geom_density (only x has to be specified):

mydiamonds %>% 
  ggplot() +
  geom_density(aes(x=price))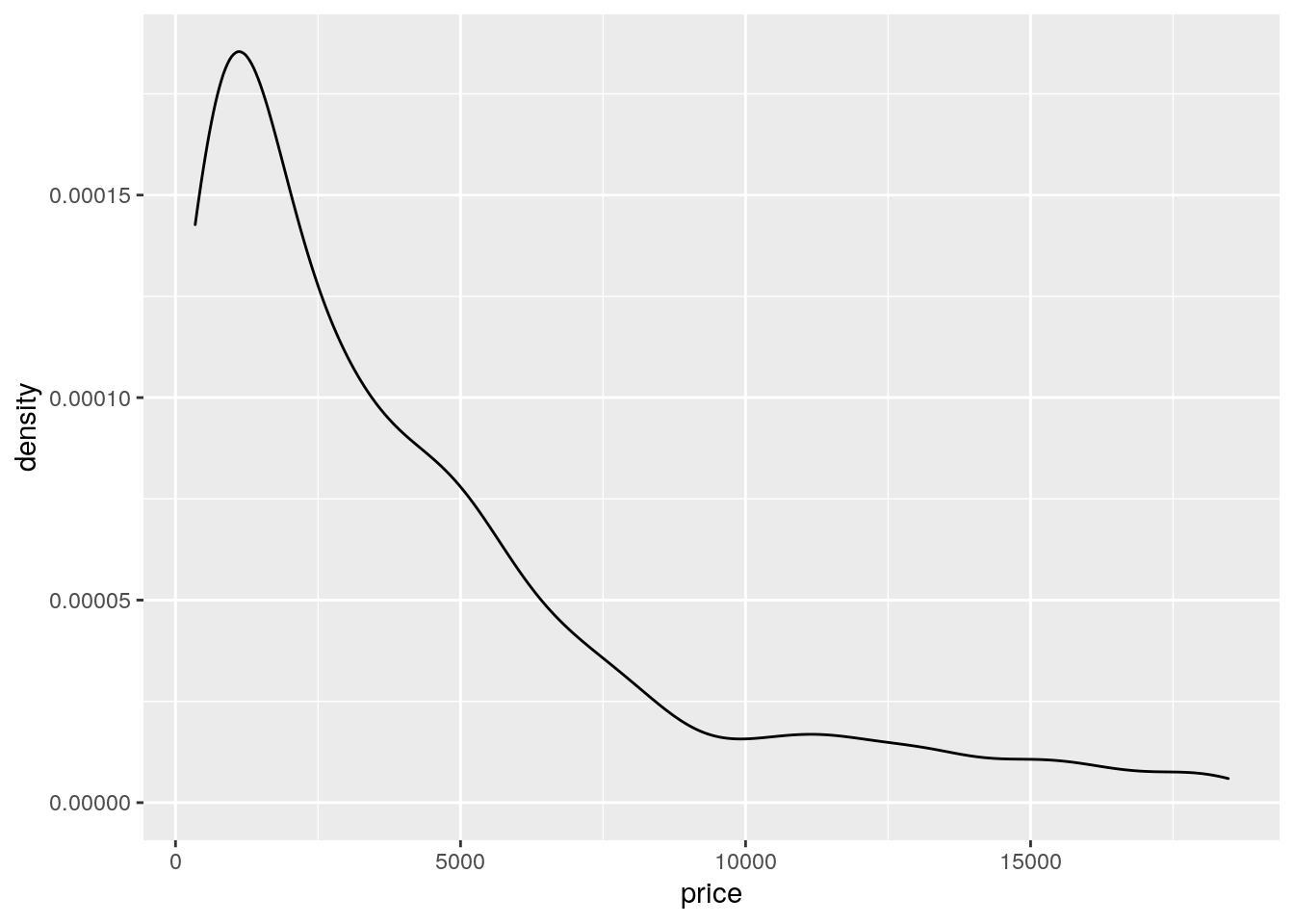

Note that the y-axis range is completely different with respect to the one of the histogram.

To combine together in a single plot the histogram and the density function, it is first of all necessary to produce an histogram which uses on the y-axis density instead of counts. The old approach to obtain density also in the y-axis of the histogram uses y=..density... A more modern approach adopts the function after_stat which refers to the generated variable density:

mydiamonds %>% 
  ggplot() +
  geom_histogram(aes(x=price,y=after_stat(density)),
                 fill="lightblue",color="black") +
  geom_density(aes(x=price))
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.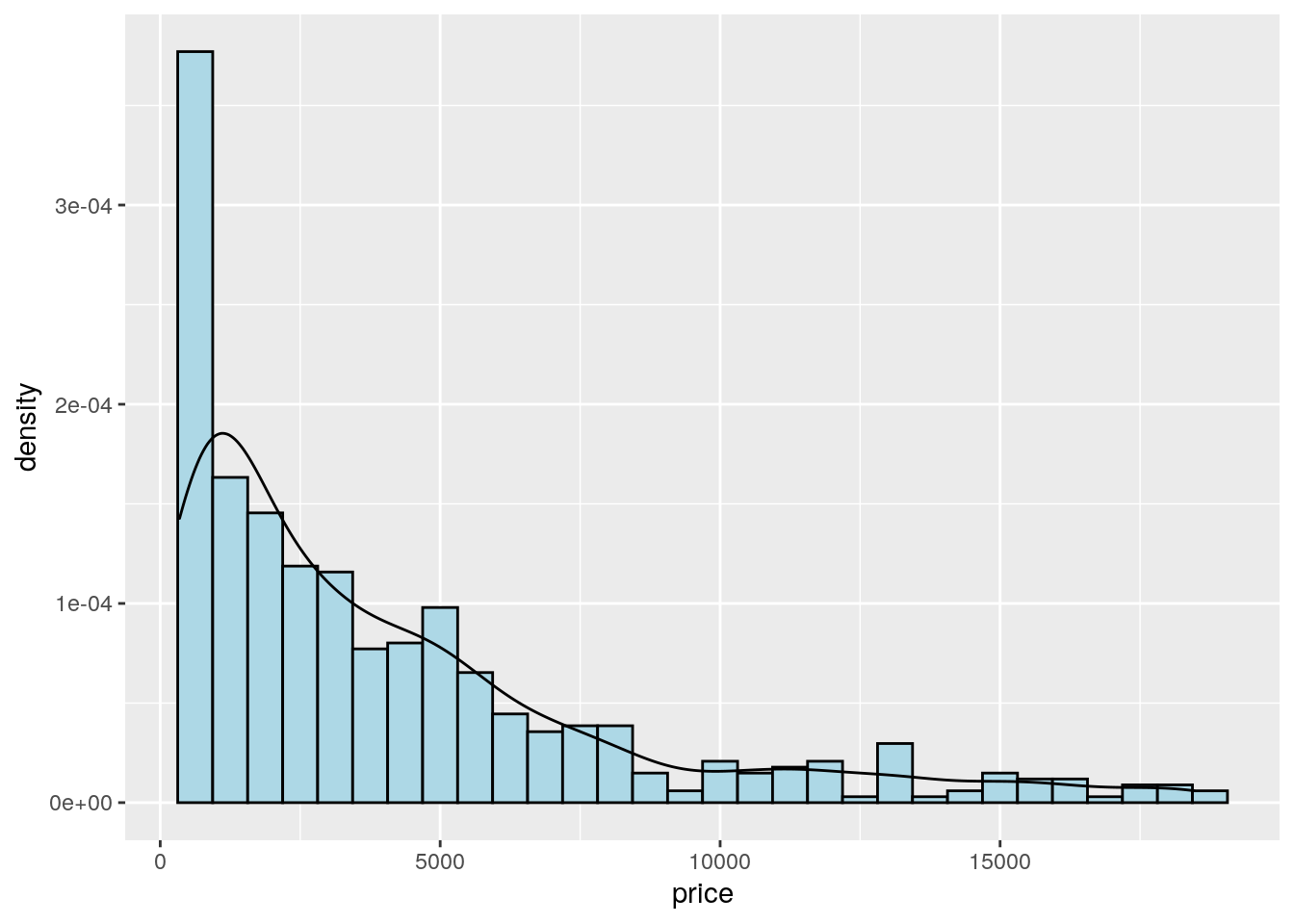

Note that the aes settings can be specified separately for each layer or globally in the ggplot function. See here below for a different specification (global now) of the previous plot:

mydiamonds %>% 
  ggplot(aes(x=price)) + # your global specifications
  geom_histogram(aes(y=after_stat(density)),
                 fill="lightblue",color="black") +
  geom_density()
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.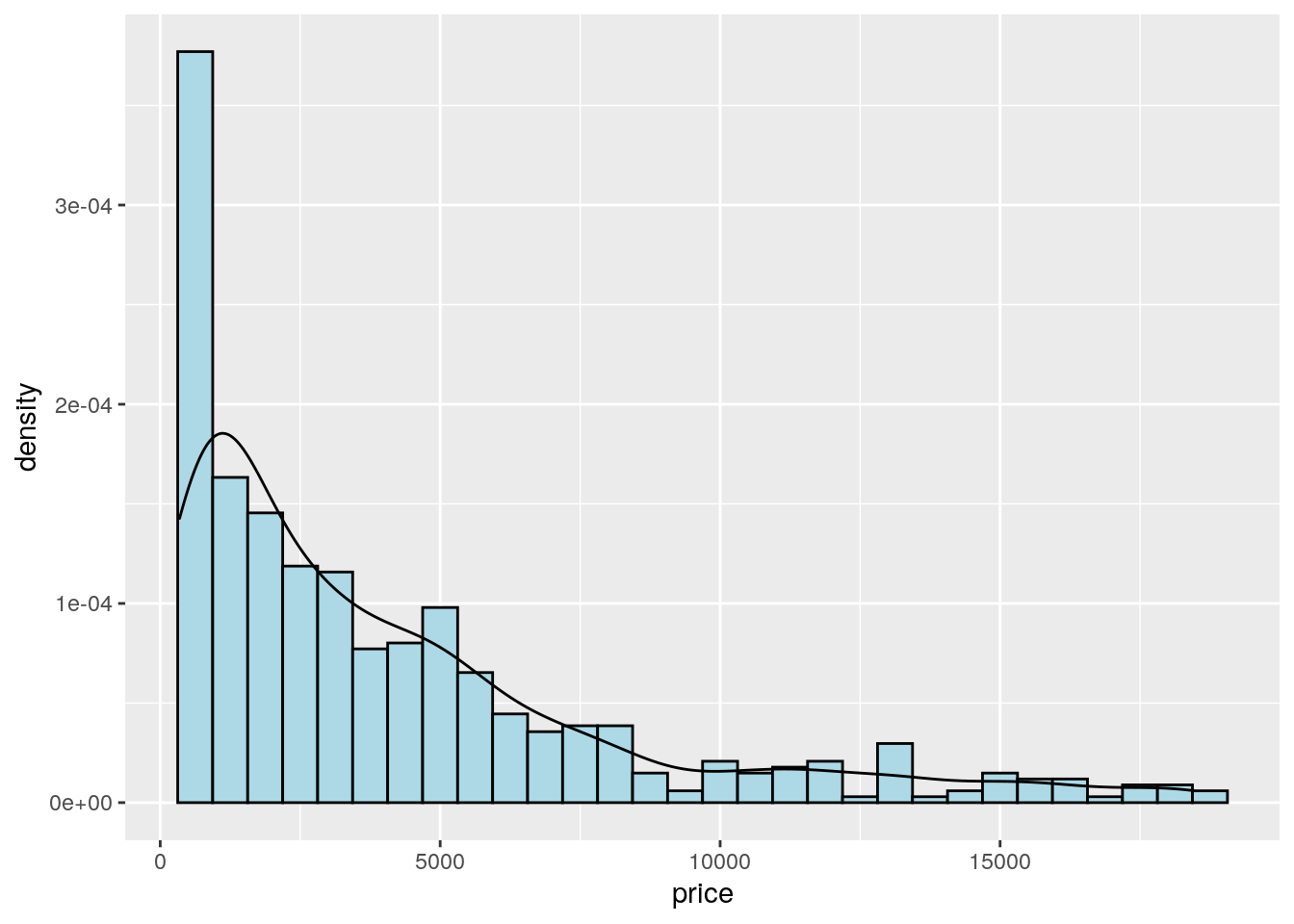

We can also display in the same plot several density estimates according to the categories of a factor like cut:

mydiamonds %>% 
  ggplot() +
  geom_density(aes(x=price,fill=cut),
               alpha = 0.5)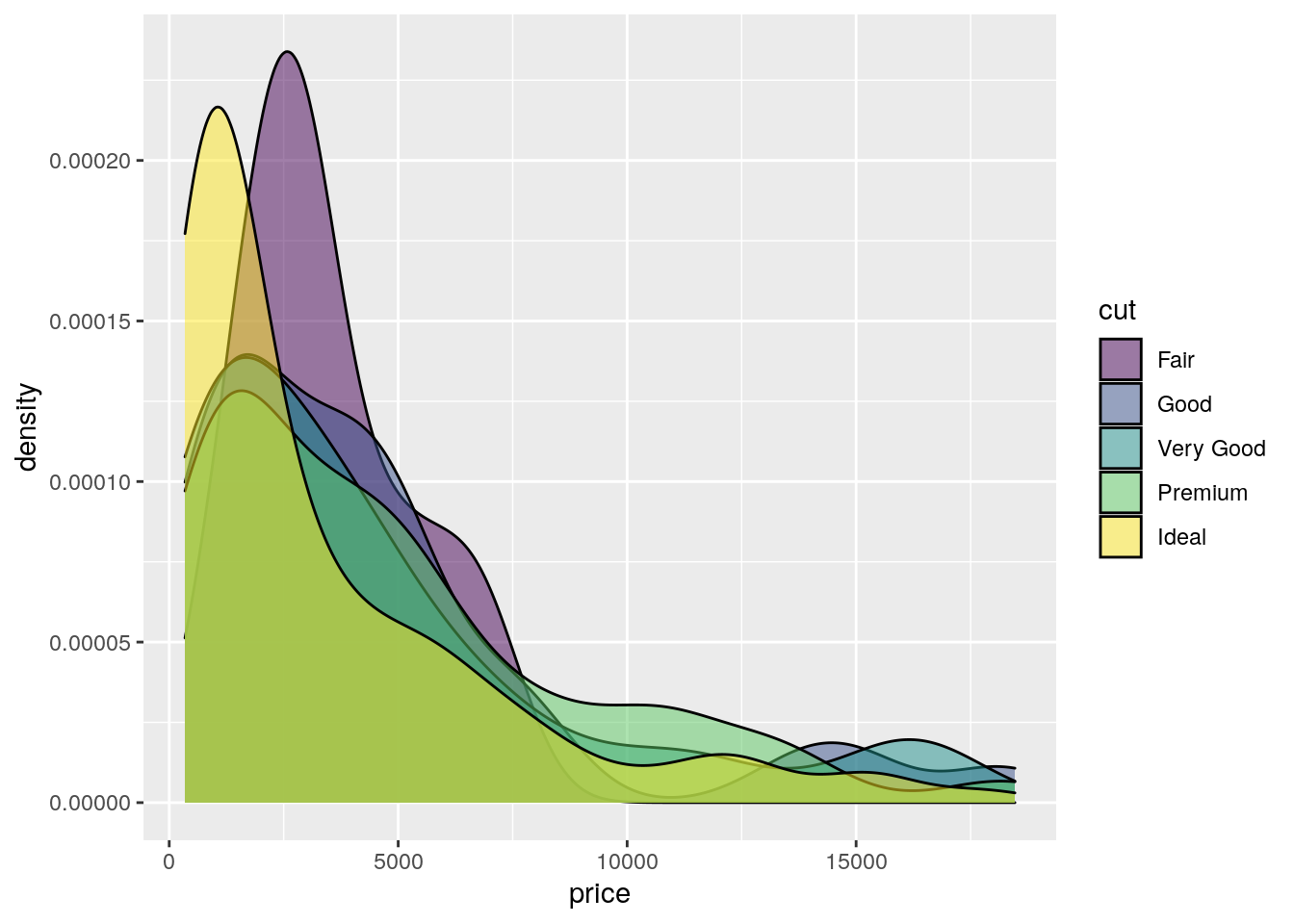

The option alpha which can take values between 0 and 1 specifies the level of transparency.

7.5.4 Barplot

The barplot can be used to represent the distribution of a categorical variable, such as for example cut. It can be obtained by using the geom_bar geometry:

mydiamonds %>% count(cut)
## # A tibble: 5 × 2
##   cut           n
##   <ord>     <int>
## 1 Fair         20
## 2 Good         61
## 3 Very Good   106
## 4 Premium     140
## 5 Ideal       212
mydiamonds %>% 
  ggplot() +
  geom_bar(aes(x=cut))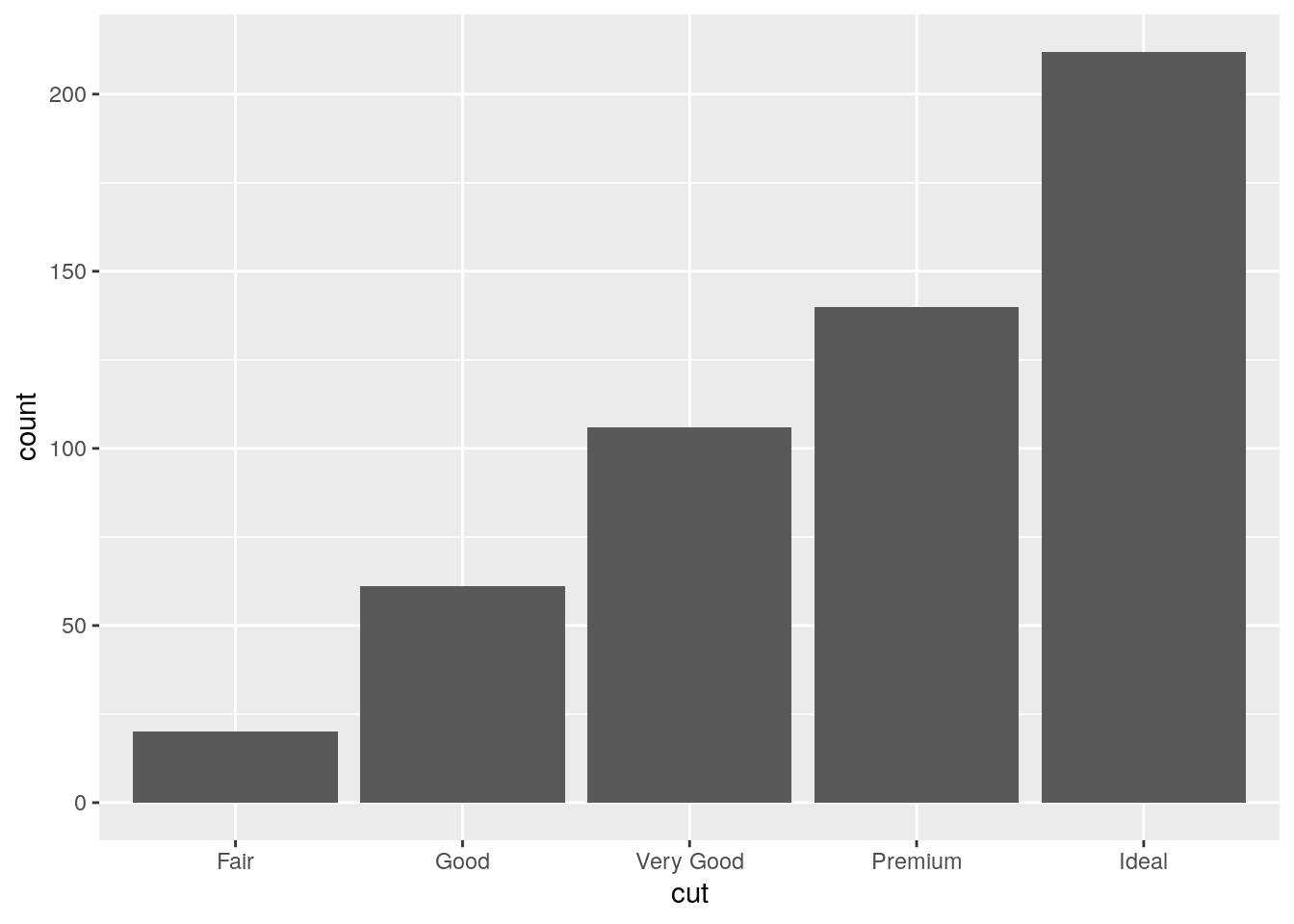

Similarly to the histogram, the y-axis is computed automatically and is given by counts (for geom_bar we have that stat="count"). If we are interested in percentages instead of absolute counts we can use two different approaches: one uses the geom_col geometry while the other uses the after_stat function. See here below.

Approach 1 (note that the first 3 lines of code computes the percentage distribution)

mydiamonds %>% 
  count(cut) %>% 
  mutate(perc = n/nrow(mydiamonds)*100) %>% 
  ggplot() +
  geom_col(aes(x=cut,y=perc))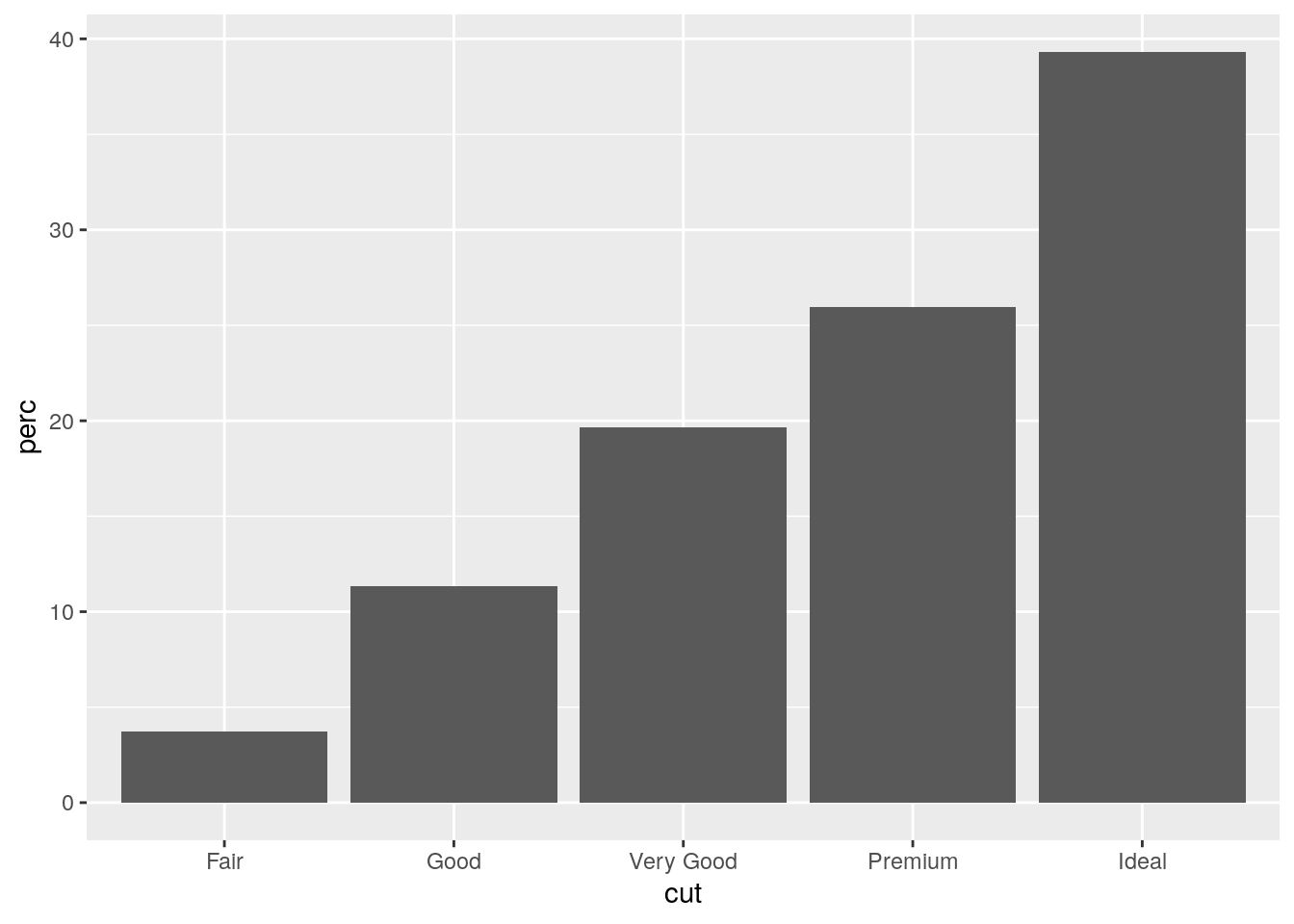

Approach 2

mydiamonds %>% 
  ggplot() +
  geom_bar(aes(x=cut,
               y=after_stat(count/nrow(mydiamonds)*100)))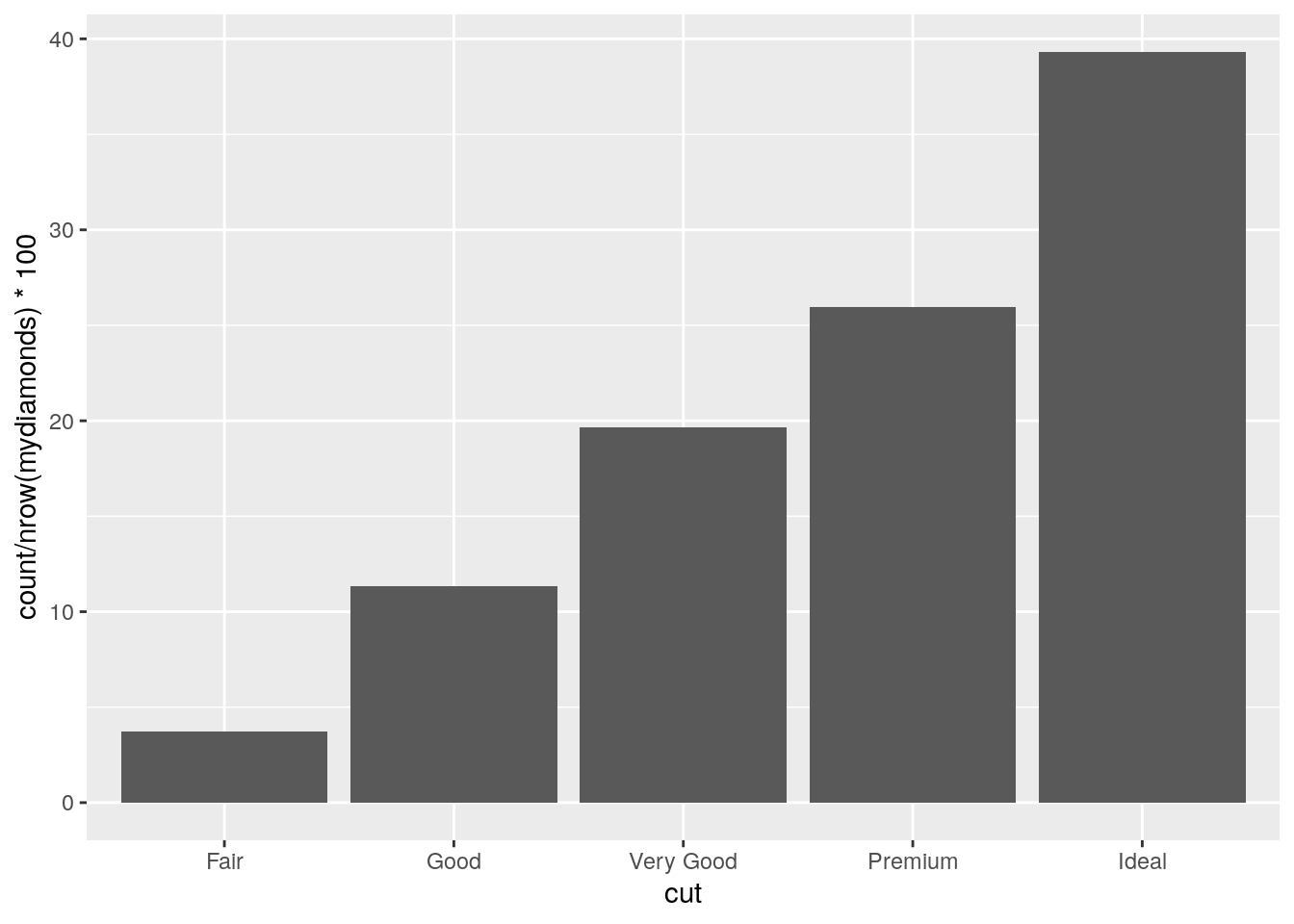

It is also possible to take into account in the barplot another qualitative variable such as for example color when studying their joint distribution:

mydiamonds %>% 
  count(cut, color)
## # A tibble: 33 × 3
##    cut   color     n
##    <ord> <ord> <int>
##  1 Fair  D         1
##  2 Fair  E         2
##  3 Fair  F         6
##  4 Fair  G         7
##  5 Fair  H         4
##  6 Good  D         9
##  7 Good  E        12
##  8 Good  F        11
##  9 Good  G        10
## 10 Good  H         7
## # … with 23 more rows

In particular color can be used to set the bar fill aesthetic:

mydiamonds %>% 
  ggplot() +
  geom_bar(aes(x=cut, fill=color))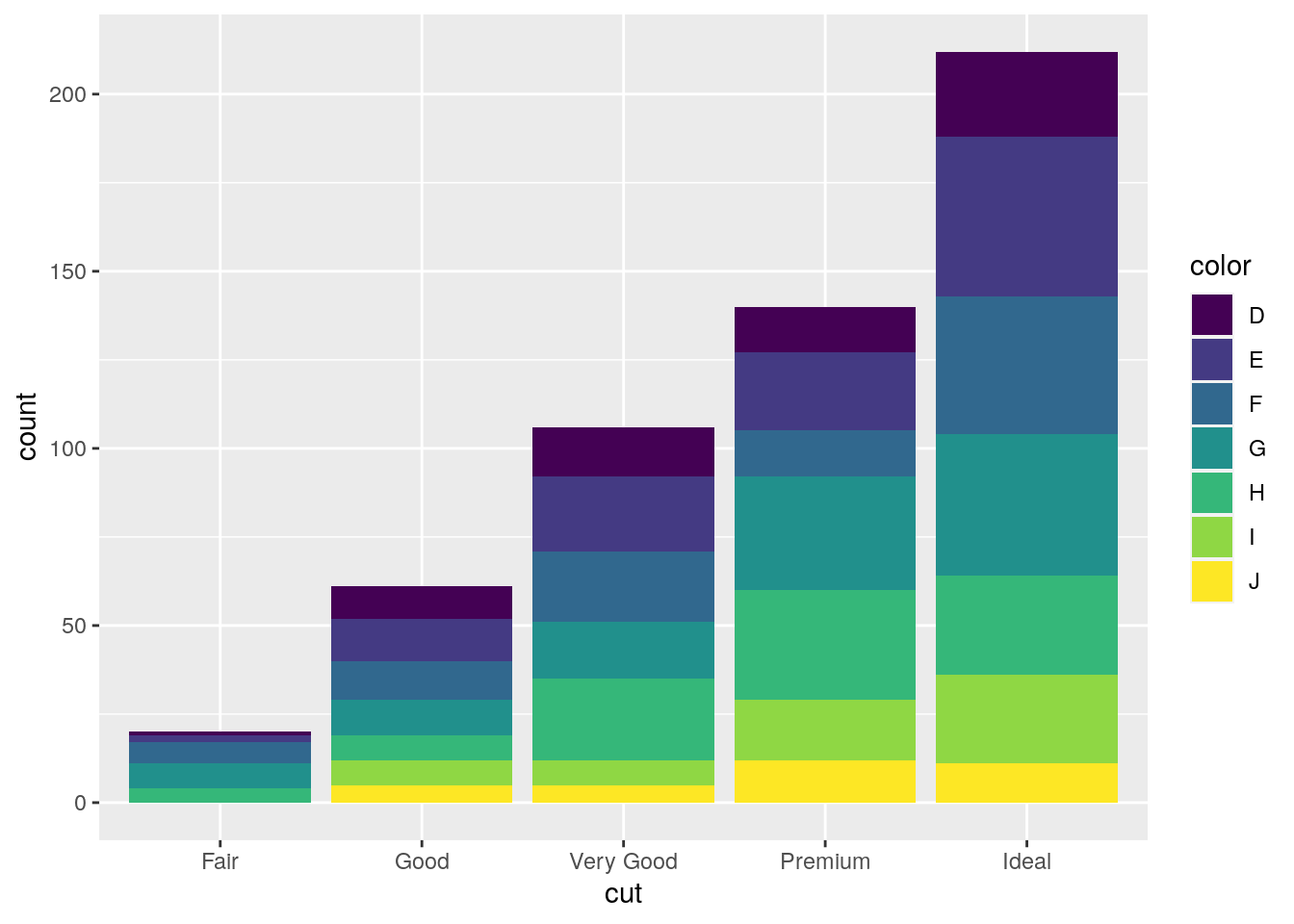

Note that the bars are automatically stacked and each colored rectangle represents a combination of cut and clarity. The stacking is performed automatically by the position adjustment given by the position argument (by default it is set to position = "stack"). Other possibilities are "dodge" and "fill":

#side by side bars
mydiamonds %>% 
  ggplot() +
  geom_bar(aes(x=cut, fill=clarity), 
           position = "dodge") 

#stacked bar with the same height (100%)
mydiamonds %>% 
  ggplot() +
  geom_bar(aes(x=cut, fill=clarity), 
           position = "fill")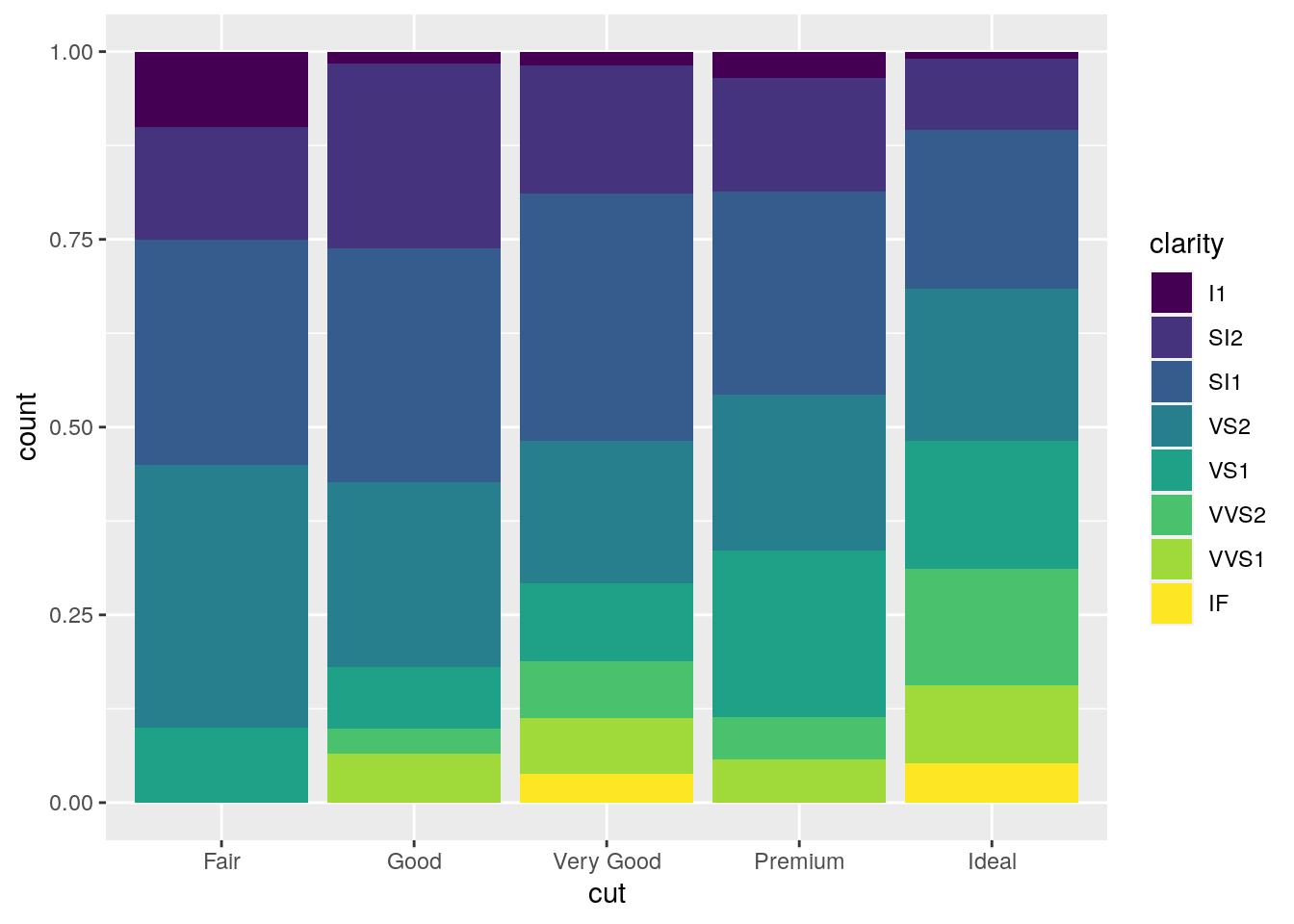

The option position = "fill" is similar to stacking but each set of stacked bars has the same height (corresponding to 100%); this makes the comparison between groups easier. The option position = "dodge" places the rectangles side by side.

An alternative consists in the use of facet_wrap that will create 8 separate plots (as the number of categories of clarity) each representing the conditional cut distribution:

mydiamonds %>% 
  ggplot() +
  geom_bar(aes(x=cut, fill=color),
           position = "fill") +
  facet_wrap(~clarity)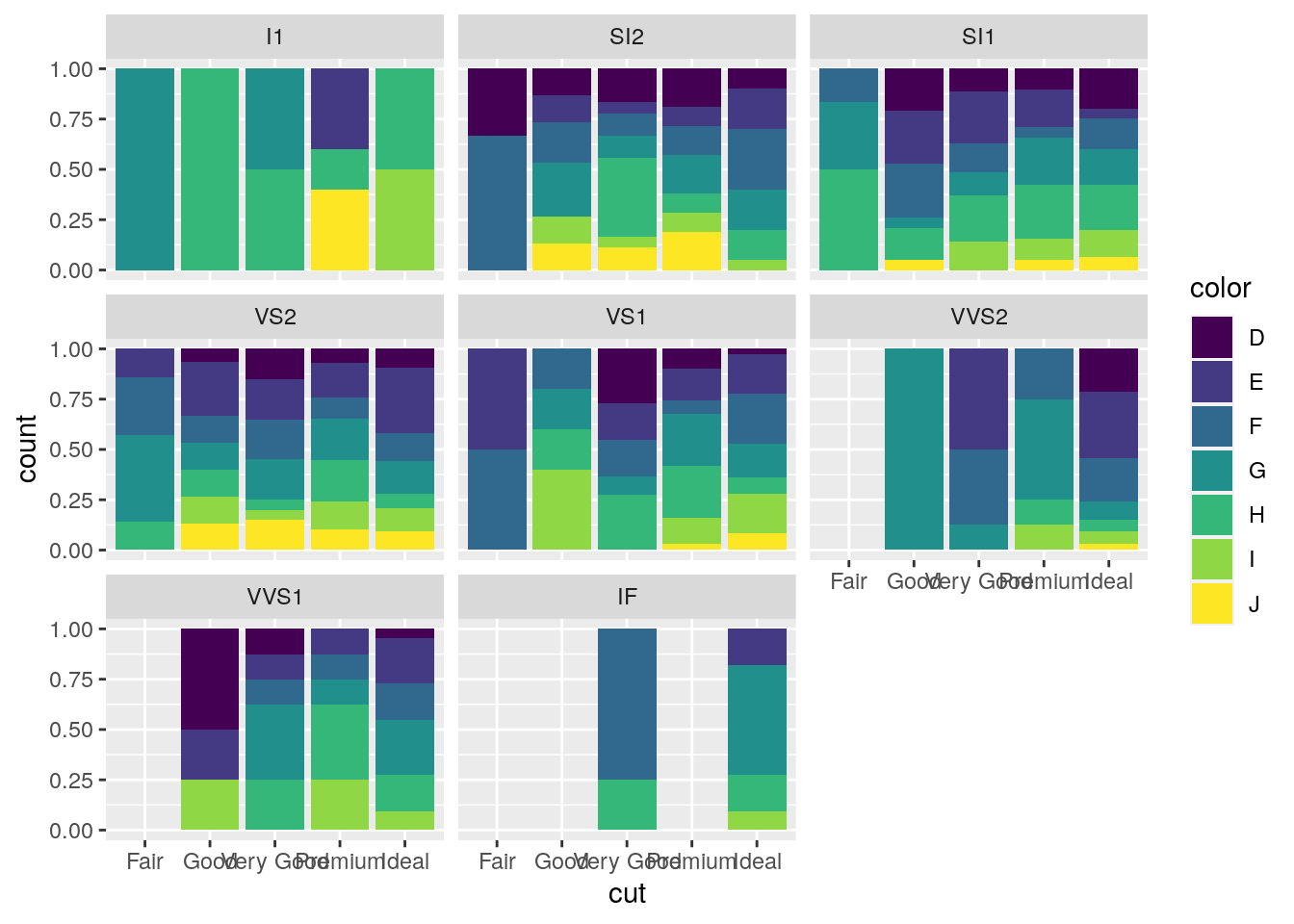

7.6 Data import

Assume we have some data available from a csv file (for example fev.csv). Note that a csv file can be open using a text editor (e.g. TextNote, TextEdit).

There are 3 things that characterize a csv file:

  • the header: the first line containing the names of the variables;
  • the field separator (delimiter): the character separating the information (usually the semicolon or the comma is used);
  • the decimal separator: the character used for real number decimal points (it can be the full stop or the comma).

In the considered csv file (try to open it with a text editor):

  • the header is given by a set of text strings:
  • “,” is the field separator;
  • “.” is the decimal separator.

All this information are required when importing the data in R by using the read.csv function, whose main arguments are reported here below (see ?read.csv):

  • file: the name of the file which the data are to be read from; this can also including the specification of the folder path (use quotes to specify it);
  • header: a logical value (T or F) indicating whether the file contains the names of the variables as its first line;
  • sep: the field separator character (use quotes to specify it);
  • dec: the character used in the file for decimal points (use quotes to specify it).

The following code is used to import the data available in the fev.csv file. The output is an object named fevdata:

fevdata <- read.csv("files/fev.csv")

The argument header=T, sep="," and dec="." are set to the default value (see ?read.csv) and they could be omitted.

Alternatively, it is possible to use the user-friendly feature provided by RStudio: read here for more information. The data import feature can be accessed from the environment (top-right) panel (see Figure 7.5). Then all the necessary information can be specified in the following Import Dataset window as shown in Figure 7.6.

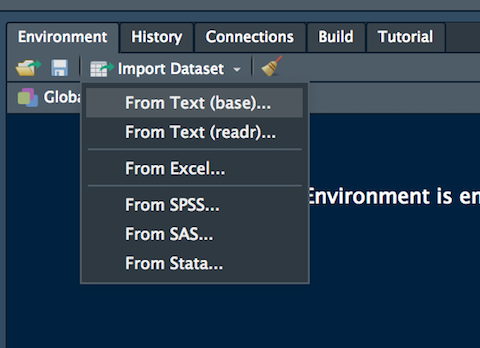
The Import Dataset feature of RStudio

Figure 7.5: The Import Dataset feature of RStudio

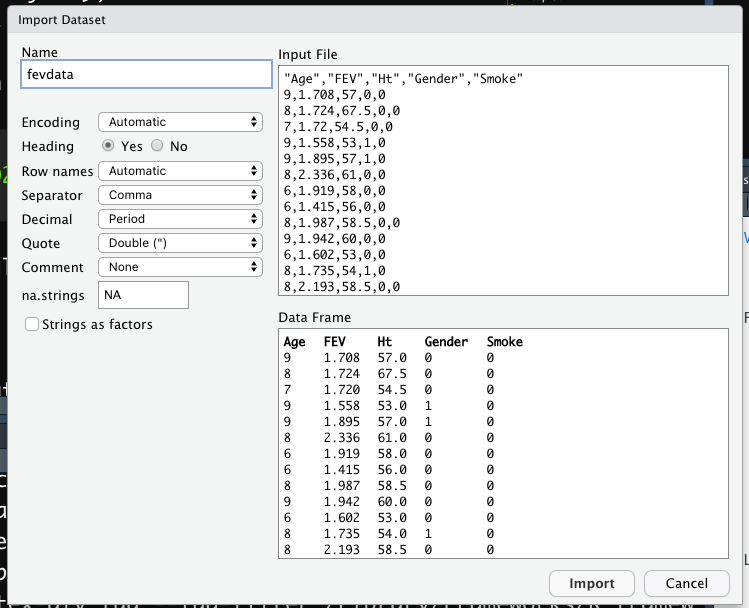
Specification of the csv file characteristics through the Import Dataset feature

Figure 7.6: Specification of the csv file characteristics through the Import Dataset feature

After clicking on Import an object named fevdata will be created (essentially this RStudio feature makes use of the read.csv function).

The fevdata is an object of class data.frame:

class(fevdata)
## [1] "data.frame"

Data frames are matrix of data where you can find subjects (in this case each day) in the rows and variables in the column (in this case you have the following variables: dates, AAPL prices, etc.).

By using str or glimpse we get information about the type of variables included in the data frame:

str(fevdata)
## 'data.frame':    654 obs. of  5 variables:
##  $ Age   : int  9 8 7 9 9 8 6 6 8 9 ...
##  $ FEV   : num  1.71 1.72 1.72 1.56 1.9 ...
##  $ Ht    : num  57 67.5 54.5 53 57 61 58 56 58.5 60 ...
##  $ Gender: int  0 0 0 1 1 0 0 0 0 0 ...
##  $ Smoke : int  0 0 0 0 0 0 0 0 0 0 ...
glimpse(fevdata)
## Rows: 654
## Columns: 5
## $ Age    <int> 9, 8, 7, 9, 9, 8, 6, 6, 8, 9, 6, 8, 8, 8, 8, 7, 5, 6, 9, 9, 5, …
## $ FEV    <dbl> 1.708, 1.724, 1.720, 1.558, 1.895, 2.336, 1.919, 1.415, 1.987, …
## $ Ht     <dbl> 57.0, 67.5, 54.5, 53.0, 57.0, 61.0, 58.0, 56.0, 58.5, 60.0, 53.…
## $ Gender <int> 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, …
## $ Smoke  <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …

It is possible to get a preview of the top or bottom part of the data frame by using head or tail:

head(fevdata) #preview of the first 6 lines 
##   Age   FEV   Ht Gender Smoke
## 1   9 1.708 57.0      0     0
## 2   8 1.724 67.5      0     0
## 3   7 1.720 54.5      0     0
## 4   9 1.558 53.0      1     0
## 5   9 1.895 57.0      1     0
## 6   8 2.336 61.0      0     0
tail(fevdata) #preview of the last 6 lines 
##     Age   FEV   Ht Gender Smoke
## 649  16 4.872 72.0      1     1
## 650  16 4.270 67.0      1     1
## 651  15 3.727 68.0      1     1
## 652  18 2.853 60.0      0     0
## 653  16 2.795 63.0      0     1
## 654  15 3.211 66.5      0     0

Use the following alternative functions if you want to get information about the dimensions of the data frame:

nrow(fevdata) #number of rows
## [1] 654
ncol(fevdata) #number of columns
## [1] 5
dim(fevdata) #no. of rows and columns
## [1] 654   5

7.7 Exercises Lab 5

7.7.1 Exercise 1

Consider the data available in the fev.csv file (use fevdata as the name of the data frame). The dataset examines if respiratory function in children was influenced by exposure to smoking at home. The included variables are:

  • Age
  • FEV: forced expiratory volume in liters (lung capacity)
  • Ht: height measured in inches
  • Gender: 0=female, 1=male
  • Smoke: exposure to smoking (0=no, 1=yes)

  1. Import the data in R and check the type of variables contained in the dataframe (use the read.csv function by means of the Import feature of RStudio in the top-right panel). Check the structure of the data.

  2. Compute the univariate and bivariate contingency table (with percentage frequencies) for Gender and Smoke.

  3. Represent graphically height, age and FEV by histogram or barplot. Avoid using count on the y-axis. Comment the plots.

  4. Using boxplots study the distribution of Age and then Ht conditioned on Gender (in this case you need to transform Gender into a factor with factor(Gender)). Comment the plots.

  5. Using a scatterplot represent FEV as a function of Ht. Use different colors according to the smoke information (use factor(Smoke)). Comment.

  6. Produce different scatterplots representing FEV as a function of Ht according to the gender categories (use factor(Gender)). Include also in the plots a smooth line. Comment the plots.

7.7.2 Exercise 2

Consider the Titanic data contained in the file titanic_tr.csv. This is a subset (with 891 observations and 11 variables) of the original dataset. The included variables are the following:

  • pclass: passenger class (first, second or third)
  • survived: survived (1) or died (0)
  • name: passenger name
  • sex: passenger sex
  • age: passenger age
  • sibSp: number of siblings/spouses aboard
  • parch: number of parents/children aboard
  • ticket: ticket number
  • fare: fare (cost of the ticket)
  • cabin: cabin id
  • embarked: port of embarkation (S = Southampton, C = Cherbourg, Q = Queenstown)
  1. Import the data and explore them. Transform the variable survived, pclass and sex into factors using the following code (mydata is the name of the data frame):
mydata$pclass = factor(mydata$pclass)
mydata$survived = factor(mydata$survived)
mydata$sex = factor(mydata$sex)
  1. Represent graphically the distribution of the variable fare. Moreover, compute the average ticket price paid by passengers. Finally, compute the percentage of tickets paid more than 100$.
  2. Represent graphically the distribution of the variable age. Compute the average age. Pay attention to missing values. Consider the possibility of using the na.rm option of the function mean (see ?mean).
  3. Study the distribution of sex by using a barplot. Derive also the corresponding table frequency distribution.
  4. By using a graphical representation study the distribution of age conditionally on gender. Moreover, compute the mean age by gender.
  5. Compute the (absolute and percentage) bivariate distribution of sex and survived (percentages should be computed with respect to the total sample size). Moreover, produce the corresponding plot which represents the two factors.
  6. Derive the percentage distribution of survived conditioned on sex. Produce also the corresponding plot.
  7. Filter by sex and consider only males and compute the frequency distribution of the variable embarked. Produce the corresponding plot.
  8. Create a new variable called agecat with two categories (minor if age < 18, major otherwise). Then derive the frequency distribution of agecat.
  9. Produce a scatterplot with age on the x-axis and fare on the y-axis. Use a different point color according to gender.
  10. Study the relationship between age and fare, as you did in the previous sub-exercise, producing sub-plots according to embarked.