1.1 Theoretical Probability
When each of the outcomes in the sample space of a random experiment can be reasonably assumed to be equally likely then the probability of any outcomes or events can be determined in advance. This is called theoretical probability.
Sample spaces and equally-likely outcomes
Equally-likely outcomes typically arise from the symmetry of a physical object (such as a coin or die) or a reasonable assumption. For example, when considering the day a randomly chosen person was born on, it seems reasonable to assume any day of the week is equally likely.
Since sample spaces contain every possible outcome, the probability that the outcome of a trial is contained in the sample space is 1, meaning it is certain. Hence, the probability of each outcome is \(\frac{1}{N}\) where \(N\) is the number of outcomes.

Events
An event is typically a set of outcomes. Assuming the outcomes are equally likely, the probability of an event occurring can be calculated. Note that for any event:
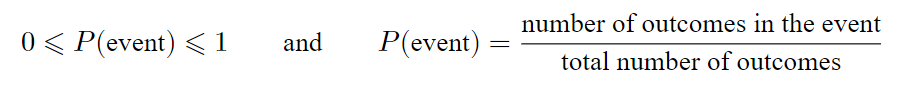

It can help to write out sample spaces. Some sample spaces can be easily described using a simple list, but more organisation may be needed for more complicated sample spaces, such as approaching the list in a systematic manner or using a grid. Remember that sample spaces are seldom useful if each of the outcomes is not equally likely.
If two coins are tossed:
Not equally likely outcomes: \(\{\text{no tails},\text{one tails},\text{two tails}\}\)
Equally likely outcomes: \(\{\text{HH},\text{HT},\text{TH},\text{TT}\}\)