3 偏微分

偏微分とは，多変数関数についての微分である．これまでは基本的に一変数の関数 $f(x)$ のようなものしか扱ってこなかった．

しかし，統計や機械学習におけるモデルの学習とは，ほとんどが多数のパラメータをある意味で最適化することになり，その際には多変数関数の微分の知識が必要になる．

ここでは，微分の操作が，一変数から多変数に拡張された時にどのようになるのかを紹介していく．

Definition 3.1 (多変数関数) 多変数関数とは以下のように変数を複数持ち，出力が一つであるような関数を指す． $\begin{align} y = f(x_{1},\ldots,x_{n}) \end{align}$

また，入力する変数をベクトルにまとめた場合は， $f(\boldsymbol x)$ のように表記することもある．

3.1 偏微分と方向微分

まず，二変数関数の場合について議論を進める．基本的にはそのまま多変数は容易に拡張される．

Definition 3.2 (偏微分・偏導関数) 二変数関数 $f(x,y)$ について， $(x,y) = (a,b)$ での $x$ に関する偏微分は，

$\begin{align} {\partial f \over \partial x}(a,b) = \lim_{h \rightarrow 0} {f(a+h, b) - f(a,b) \over h} \end{align}$

と定義され， $y$ に関する偏微分は

$\begin{align} {\partial f \over \partial y}(a,b) = \lim_{h \rightarrow 0} {f(a, b+h) - f(a,b) \over h} \end{align}$

と定義される．これらの極限が存在する時，それぞれ $f(x,y)$ は $(x,y) = (a,b)$ で $x$ について偏微分可能， $y$ について偏微分可能という．

また， $f(x,y)$ の各点での $x$ に関する偏微分を表す関数， $y$ に関する偏微分を表す関数

$\begin{align} {\partial f \over \partial x}(x,y) = \lim_{h \rightarrow 0} {f(x+h, y) - f(x,y) \over h} \end{align}$

$\begin{align} {\partial f \over \partial y}(x,y) = \lim_{h \rightarrow 0} {f(x, y+h) - f(x,y) \over h} \end{align}$

をそれぞれ $x,y$ に関する偏導関数という．

偏導関数を表す記号は上記の $\partial f \over \partial x$ 以外にも $f_x$ のように左下に対象の変数を記載する流儀もある．

Exercise 3.1 (偏微分1)

次の二変数関数

$f(x,y)$ について，

$x,y$ それぞれの偏導関数を求めよ．

一変数の微分の場合，極限を動かす方向は正負の２パターンしかなかったが，二変数の場合，は色々な方向に動かすことを考えられる．

そこで，次に任意の方向 $\boldsymbol u = (\alpha, \beta)$ にについての微分を考えよう．

Theorem 3.1 (方向微分) 二変数関数 $f(x,y)$ の $(x,y) = (a,b)$ での $\boldsymbol u = (\alpha, \beta)(\neq (0, 0))$ 方向の偏微分 $f_{\boldsymbol u}(a,b)$ は

$\begin{align} f_{\boldsymbol u}(a,b) &= \lim_{h \rightarrow 0} {f(a + h \alpha, b + h \beta) - f(a,b) \over h} \\ &= \alpha f_x(a,b) + \beta f_y (a,b) \end{align}$

となる．

ここで， $f(x,y)$ の $(x,y = (a,b))$ での $x$ 方向への偏微分と， $y$ 方向への偏微分から成るベクトル $(f_x(a,b), f_y(a,b))$ を $f(x,y)$ の $(x,y) = (a,b)$ での勾配(gradient)という．勾配は， $f(x,y)$ が $(x,y)=(a,b)$ において最も急速に増大する方向を表す．

また，特定の曲線方向に関して考えることも可能で， $xy$ 平面上の曲線を $(g(t), h(t))$ で表せば，二変数関数 $f(x,y)$ の $(x,y) = (g(t), h(t))$ 上での断面を考えることができる．

この時，この断面の関数は $t$ の関数として $f(g(t), h(t))$ と表せて，この関数の微分を以下のように扱うことができる．

Theorem 3.2 (xy平面上の曲線上での微分) 二変数関数 $f(x,y)$ について， $xy$ 平面上の曲線 $(g(t), h(t))$ 上での微分は以下のようになる．

$\begin{align} f(g(t), h(t))' = f_x(g(t), h(t)) g'(t) + f_y(g(t), h(t)) h'(t) \end{align}$

3.2 偏微分の応用

二変数関数の微分についても，高階導関数を考えることができる．ただし，二変数のどちらに関して微分を行うかによって分岐していくことになる．

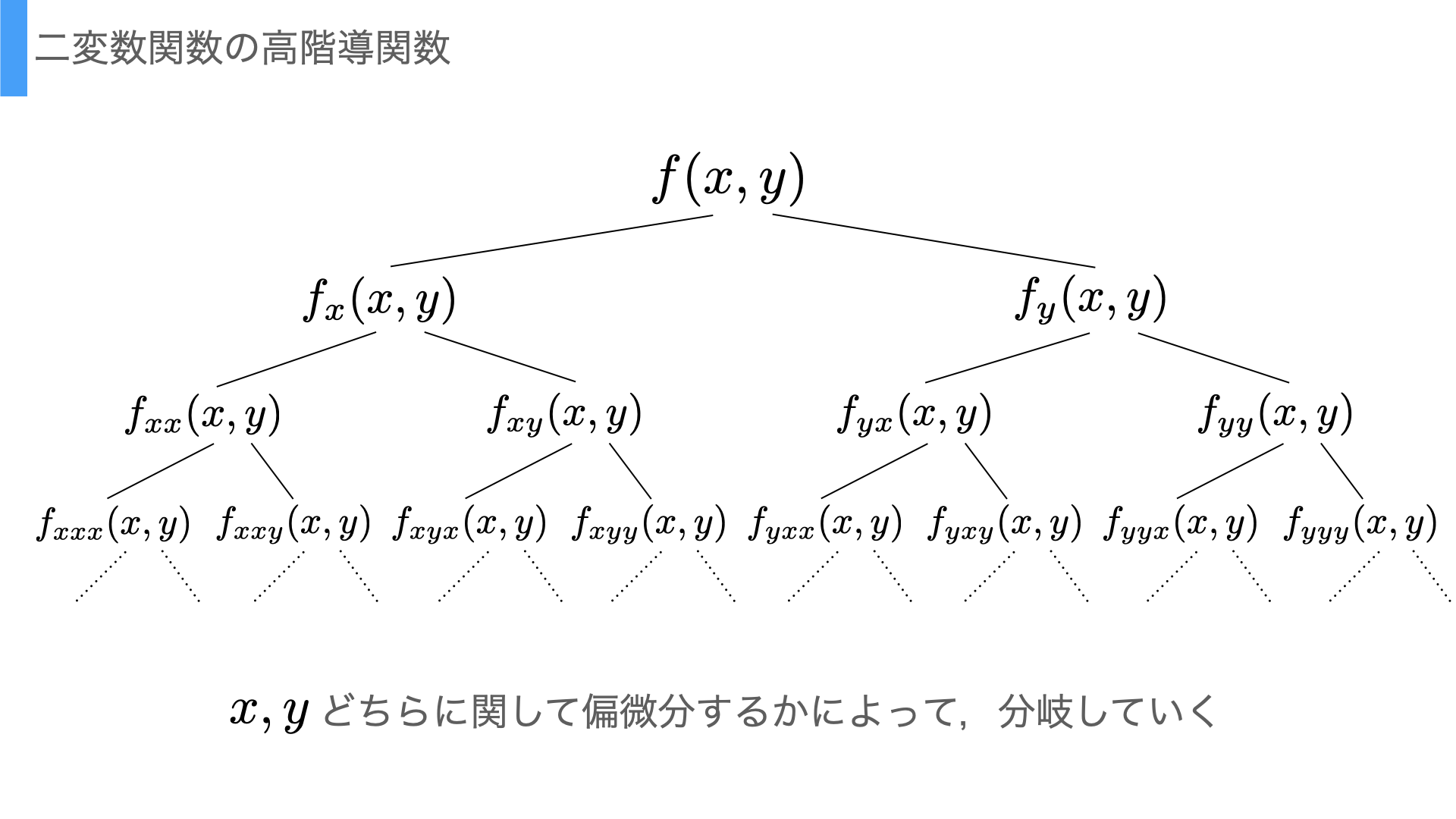
Figure 3.1: 偏微分の高階導関数の分岐

その際，記号の定義としては， $x$ に関する偏導関数 $f_x$ をさらに $x$ に関して偏微分したものを $f_{xx}$ ， $y$ については $f_{xy}$ などと表現したり，または ${\partial^2f(x,y) \over \partial y \partial x}$ としてこれを $f$ の $y$ に関する偏導関数をさらに $x$ で偏微分したものと表現したりする．

Exercise 3.2 (高階偏導関数の表現) 次の記号がどのような偏導関数を表しているか述べよ．

$f_{xyy}(x,y)$
$\frac{\partial^4f(x,y)}{\partial x \partial y \partial x \partial y \partial y}$
$f_{xyz}(x,y,z)$ （これは三変数関数である）．

3.2.1 実際の計算

高階の偏導関数は，実際にはある変数についての関数の微分をただ繰り返し行うだけでありさほど難しい手続きではない．

Exercise 3.3 (高階偏導関数) いま， $f(x,y) = x^3 + 2x^2y - 3y^2 + \cos x$ を考える．この時，以下を求めよ．

$f_x(x,y)$
$f_y(x,y)$
$f_{xx}(x,y)$
$f_{xy}(x,y)$
$f_{yx}(x,y)$
$f_{yy}(x,y)$

3.3 二変数関数の極値

二変数関数においても，極値を考えることはできる．イメージとしては図3.2の谷底・山の頂点に当たる点で，それぞれ極小値・極大値などと呼ぶ．

library(plotly)

f <- function(x,y) {
  xy <- expand.grid(x,y)
  z  <- apply(xy, 1, function(e){
    x <- e[1]
    y <- e[2]
    x*exp(-(x^2 + y^2)/2)
  })
  return(z)
}
x <- seq(-3, 3, 0.05)
y <- seq(-3, 3, 0.05)
row_size <- length(x)
z <- f(x,y) %>% matrix(nrow=row_size, byrow=T)

scene = list(camera = list(eye = list(x = -0.5, y = 1.25, z = 0.3)))

fig <- plot_ly(x = ~x, y = ~y, z = ~z)
fig <- fig %>% add_surface()
fig <- fig %>% plotly::layout(scene = scene)

fig

Figure 3.2: 二変数関数の3Dプロット

ちなみに，この図の関数は以下である．

$\begin{align} f(x,y) = x \exp(-(x^2 + y^2)/2) \tag{3.1} \end{align}$

Theorem 3.3 (二変数関数の極値) 二変数関数 $f(x,y)$ が $(x,y) = (a,b)$ で極値を持つならば， $f_x(a,b) = f_y(a,b) = 0$ が成り立つ．

ただし，theorem3.3は極値であれば偏微分の値が $0$ であると言っているだけであり， $x,y$ それぞれの偏微分の値が $0$ である点が必ずしも極値であることを保証していない．これは， $x$ 軸と $y$ 軸というたった２方向の直線上での微分での変化が0ということを言っているだけであることを考えれば当然である．

Theorem 3.4 (二変数関数の極値の候補) 二変数関数 $f(x,y)$ について $(x,y) = (a,b)$ が $f_x(a,b) = f_y(a,b) = 0$ で極値の候補であるとする．このとき，次のような行列 $H$ を考える．

$\begin{align} H = \begin{pmatrix} f_{xx}(a,b) & f_{xy}(a,b) \\ f_{yx}(a,b) & f_{yy}(a,b) \end{pmatrix} \end{align}$

この $H$ の行列式の値によって以下のように判定が行える．

$|H| > 0$ であれば $(x,y) = (a,b)$ で極値を持つ．
$|H| < 0$ であれば $(x,y) = (a,b)$ で極値を持たない．
$|H| = 0$ であれば $(x,y) = (a,b)$ で極値を持つかは不明．

さらに， $|H| > 0$ のとき極小値・極大値かどうかについては以下のように判定できる．

$f_{xx}(a,b) > 0 \Rightarrow (x,y) = (a,b)$ で極小値を持つ
$f_{xx}(a,b) < 0 \Rightarrow (x,y) = (a,b)$ で極大値を持つ

また， $H$ をヘッセ行列，ヘッセ行列の行列式 $|H|$ をヘシアンと呼ぶ．

三変数以上の場合は，ヘシアンではなく，ヘッセ行列の固有値を調べる必要がある．

3.4 ニュートンラフソン法

ある関数の最小値または最大値を実際に求めたい場合に利用できるアルゴリズムを紹介する．ニュートン・ラフソン法とは，勾配の情報を利用して極値があるであろう方向に数値を反復的に更新していくアルゴリズムである．

考え方の詳細は(林賢一 2020)を参照されたい．具体的には次のような手順で実行すれば良い．

3.4.1 ニュートン・ラフソン法のアルゴリズム

初期値 $(x_0, y_0)$ を適当に定める．
現在値 $(x_n, y_n)$ に対して以下のようにして更新値 $(x_{n+1}, y_{n+1})$ を計算する．

$\begin{align} \begin{pmatrix} x_{n+1} \\ y_{n+1} \end{pmatrix} = \begin{pmatrix} x_{n} \\ y_{n1} \end{pmatrix} - H(x_n, y_n)^{-1} \begin{pmatrix} f_x(x_n, y_n) \\ f_y(x_n, y_n) \end{pmatrix} \end{align}$

ここで $H(x_n, y_n)$ はTheorem3.4で紹介したヘッセ行列に対して，その要素の偏導関数にそれぞれ $(x_n, y_n)$ を代入した値を持つ行列である．すなわち

$\begin{align} H(x_n, y_n) = \begin{pmatrix} f_{xx}(x_n, y_n) & f_{xy}(x_n, y_n) \\ f_{yx}(x_n, y_n) & f_{yy}(x_n, y_n) \end{pmatrix} \end{align}$

である．

非常に小さな値 $\epsilon$ （例えば $\epsilon = 10^{-5}$ ）に対して

$\begin{align} \sqrt{(x_n - x_{n+1})^2 + (y_n - y_{n+1})^2} < \epsilon \end{align}$

を満たせば終了．もしこれを満たさなければ改めて $(x_n, y_n) \leftarrow (x_{n+1}, y_{n+1})$ としてステップ2に戻る．

3.4.2 Rでの実装

アルゴリズムとして数値計算が可能であれば，Rで実装も可能である．ここでは次の関数を例にニュートン・ラフソン法を実行してみよう．

$\begin{align} f(x,y) = \exp(x^2 + y^2) \end{align}$

まず，１階・２階の偏導関数を求めておこう．

$\begin{align} f_{x}(x,y) &= 2x f(x,y) \\ f_{y}(x,y) &= 2y f(x,y) \\ f_{xx}(x,y) &= (2 - 2x) f(x,y) \\ f_{xy}(x,y) &= 4xy f(x,y) \\ f_{yx}(x,y) &= 4xy f(x,y) \\ f_{yy}(x,y) &= (2 - 2y) f(x,y) \\ \end{align}$

次に，この関数におけるニュートン・ラフソン法の実装例を示す．

p  <- c(0.8, 0.9) # choose initial values
ps <- matrix(p, nrow=1, byrow=T)
update_distance <- 1 # initial
eps <- 1e-5

# functions
get_update_distance <- function(p, p_next){
  return(sqrt(sum((p - p_next)^2)))
}

f   <- function(p) return(p[1]^2 + p[2]^2)
fx  <- function(p) return(2 * p[1] * f(p))
fy  <- function(p) return(2 * p[2] * f(p))
fxx <- function(p) return((2 - 2*p[1]) * f(p))
fxy <- function(p) return(4 * p[1] * p[2] * f(p))
fyx <- function(p) return(4 * p[1] * p[2] * f(p))
fyy <- function(p) return((2 - 2*p[2]) * f(p))

get_hesse <- function(p){
  res <- matrix(
    c(fxx(p), fxy(p), fyx(p), fyy(p)),
    nrow=2, byrow=T
  )
  return(res)
}

update_point <- function(p) {
  H <- get_hesse(p)
  if(det(H) == 0){
    p_next <- p
  }else{
    H_inv <- solve(H)
    p_next <- p - H_inv %*% c(fx(p), fy(p))
  }
  return(as.vector(p_next))
}

# start: newton raphson 
iteration <- 0
while(update_distance > eps){
  iteration <- iteration + 1 # count iteration
  p_next <- update_point(p)
  update_distance <- get_update_distance(p, p_next)
  p <- p_next
  ps <- rbind(ps, matrix(p, nrow=1, byrow=T)) # memory points
  
  rp <- round(p, 4)
  msg <- sprintf("update %s: x = %s, y = %s, z = %s", 
                 iteration, rp[1], rp[2], f(rp))
  print(msg)
  if(iteration > 1000) break # limit iteration
}

## [1] "update 1: x = 0.2079, y = 0.4267, z = 0.2252953"
## [1] "update 2: x = 0.105, y = -0.2857, z = 0.09264949"
## [1] "update 3: x = 0.0023, y = -0.0683, z = 0.00467018"
## [1] "update 4: x = 0, y = -0.0044, z = 1.936e-05"
## [1] "update 5: x = 0, y = 0, z = 0"
## [1] "update 6: x = 0, y = 0, z = 0"
## [1] "update 7: x = 0, y = 0, z = 0"

p_best <- p

msg <- sprintf("finish: newton-raphson. iteration: %s", iteration)
print(msg)

## [1] "finish: newton-raphson. iteration: 7"

この場合は，7回の更新で終了条件を満たしている．

最後に図3.3でニュートン・ラフソン法の更新がどのように進んでいたのか，更新点を全てプロットして可視化してみよう．

Figure 3.3: ニュートン・ラフソン法の更新の様子

オレンジの点が更新点で，それを結ぶ線が前後関係を表している．更新されるにつれて関数の底の方へと向かっていることが確認できる．

3.4.3 注意点

実はニュートン・ラフソン法はどんな関数にも使えるわけではない．初期値によっては期待している収束をしないこともあるので注意されたい．

3.5 ニュートン・ラフソン法の失敗例

最後にニュートン・ラフソン法がうまく行かない例を示す．図3.2で示したケースは初期値によっては全く期待通りに行かないことがある．

## [1] "finish: newton-raphson. iteration: 11"

この場合は，7回の更新で終了条件を満たしている．

最後に図3.3でニュートン・ラフソン法の更新がどのように進んでいたのか，更新点を全てプロットして可視化してみよう．

Figure 3.4: ニュートン・ラフソン法の更新の様子

ここでは初期値を $(0.4, -1.6)$ としてアルゴリズムを実行したが，図の通り極値とは関係のない方向に進んでいってしまっていることがわかる．

このように複雑な関数になればなるほど，極値の探索や関数の最大値・最小値を探索が困難になってくるのである．

Reference

林賢一. 2020. Rで学ぶ統計的データ解析. Edited by 下平英寿. データサイエンス入門シリーズ. 講談社サイエンティフィク.