2 重積分

一変数関数における積分とは，面積を求めることと対応していた．二変数関数を含む多変数関数について積分を拡張させたものが重積分（multiple-integral）である．

Definition 2.1 (重積分) 二変数関数\(f(x,y)\)について，領域\(R\)に関する重積分は，\(xy\)平面と\(R\)の境界と関数\(f(x,y)\)が表す曲面に囲まれる体積として定義する．ただし，\(f(x,y)>0\)の部分の体積は正として，\(f(x,y)<0\)の部分の体積は負として足し合わせる．

この体積の和を \[\begin{align} \int \int_R f(x,y) dx dy \end{align}\]

と表す．

二変数の場合は積分変数も二つとなるため，\(dxdy\)と書く．\(dxy\)ではないことに注意．

2.1 逐次積分

重積分は一変数の積分と比較すると積分領域が複雑になる．一変数の場合，定積分であれば区間\([a,b]\)を考えれば十分だったが，二変数の場合は平面状の自由な領域となる．つまり領域を\([a_x, b_x] \times [a_y, b_y]\)と考えればこれは長方形だし，楕円やもっと複雑な領域を考えることもできるのである．

Theorem 2.1 (逐次積分) 二変数関数\(f(x,y)\)の長方形領域\(I = [a,b] \times [c,d]\)上での重積分は

\[\begin{align} \int \int_I f(x,y) dxdy = \int_{c}^{d} \left( \int_{a}^{b} f(x, y) dx \right) dy = \int_{a}^{b} \left( \int_{c}^{d} f(x, y) dy \right) dx \end{align}\]

として計算できる．このとき積分の順序を交換可能である．このように一つずつ変数に着目して積分をしていく方法を逐次積分という．

この場合においては，\(x,y\)どちから積分を進めても結果は変わらないことを保証している．

Exercise 2.1 (逐次積分) \(f(x,y) = xy^2\)を\(I = \{ (x,y) | (x,y) \in [0,1] \times [0, 2] \}\)の領域で重積分したい．

\(x \rightarrow y\)の順番で逐次積分せよ
\(y \rightarrow x\)の順番で逐次積分せよ

もし，\(f(x,y) = g(x)h(y)\)のように，変数が\(x\)だけの関数と\(y\)だけの関数の積として表されていれば逐次積分は

\[\begin{align} \int \int_I f(x,y) dxdy = \int_a^b g(x) dx \times \int_c^d h(y) dy \end{align}\]

のようにそれぞれの積分の積に分解できる．ここで\(I = [a,b] \times [c,d]\)とした．

2.2 長方形以外の領域の積分

Definition 2.2 (縦線・横線領域) \(x\)に関する二つの関数\(g_1(x), g_2(x), g_1(x) \leq g_2(x)\)を用いて，領域\(R\)が

\[\begin{align} R = \{ (x,y) | a \leq x \leq b, g_1(x) \leq y \leq g_2(x) \} \end{align}\]

と表される時，領域\(R\)を縦線領域という．

また，逆に\(y\)に関する二つの関数\(h_1(y), h_2(y), h_1(y) \leq h_2(y)\)を用いて領域\(R\)が

\[\begin{align} R = \{ (x,y) | h_1(y) \leq x \leq h_2(y), c \leq y \leq d \} \end{align}\]

と表される時，領域\(R\)を横線領域という．

ここでは，円を領域とした場合の例を紹介する．

Example 2.1 (円を領域とした場合(1)) いま\(f(x,y) = xy\)を領域\(R = \{ (x,y) | x^2 + y^2 \leq 1 \}\)で積分することを考える．

\(x^2 + y^2 \leq 1\)より，明らかに\(-1 \leq x \leq 1\)である．また\(y\)を\(x\)で表すと，\(y^2 \leq 1 - x^2\)より，\(-\sqrt{1-x^2} \leq y \leq \sqrt{1-x^2}\)を得る．

すなわち，領域\(R\)を縦線領域で表すと\(R = \{ (x,y) | -1 \leq x \leq 1, -\sqrt{1-x^2} \leq y \leq \sqrt{1-x^2}\}\)となる．

従って，\(f(x,y) = xy\)を領域\(R\)で積分するには

\[\begin{align} \int \int_R f(x,y) dxdy = \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{-1}^{1} xy dx dy \end{align}\]

となる．

\(y\)の積分の区間が\(x\)の関数となっている場合，どのようにすれば良いだろうか．具体的には\(f(x,y)\)の縦線領域\(R = \{ (x,y) | a\leq x \leq b, g_1(x) \leq y \leq g_2(x) \}\)での積分は

\[\begin{align} \int_a^b \left ( \int_{g_1(x)}^{g_2(x)} f(x,y) dy \right) dx \end{align}\]

としておき，積分の結果を\(x\)の関数形を使って表せば，文字が一つ減ることになる．

Example 2.1 (円を領域とした場合(2)) Example 2.1で検討した領域\(R\)に基づいて，実際に積分を求めてみよう．

\[\begin{align} \int \int_R f(x,y) dxdy = \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{-1}^{1} xy dx dy \end{align}\]

を計算すればよかったので，まず\(y\)について積分すると

\[\begin{align} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} xy dy &= \left[ \frac12 xy^2 \right]_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \\ &= x - x^3 \end{align}\]

となる．従って求める積分は

\[\begin{align} \int_{-1}^{1} x - x^3 dx &= \left[ \frac12 x^2 - \frac14 x^4 \right]_{-1}^{1} \\ &= 0 \end{align}\]

となる．

2.3 変数変換

ここでは二変数関数の重積分について，変数変換をする場合を考える．いま簡単のため\(I = [0,1] \times [0,1], f(x,y) = 1\)としよう．この時，一辺の長さが 1の立方体を考えていることになるので体積は1となるはずである．つまり

\[\begin{align} \int \int_I 1 dxdy = 1 \tag{2.1} \end{align}\]

である．いま，

\[\begin{align} \begin{pmatrix} s \\ t \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \end{align}\]

という\((x,y)\)を\((s,t)\)に変換するとしよう．この変換は以下の図のような変換に対応する．

xy <- cbind(c(0, 0, 1, 1, 0), c(0, 1, 1, 0, 0))
A  <- matrix(c(1,5,5,2), nrow=2, byrow=T) / 5
st <- xy %*% A

bind_rows(
  as.data.frame(xy) %>% rename(x = V1, y = V2) %>% mutate(label = "Origin"),
  as.data.frame(st) %>% rename(x = V1, y = V2) %>% mutate(label = "Transformed")
) %>% 
  ggplot(aes(x=x, y=y, group=label)) + 
  geom_point() + 
  geom_polygon() + 
  facet_wrap(. ~ label)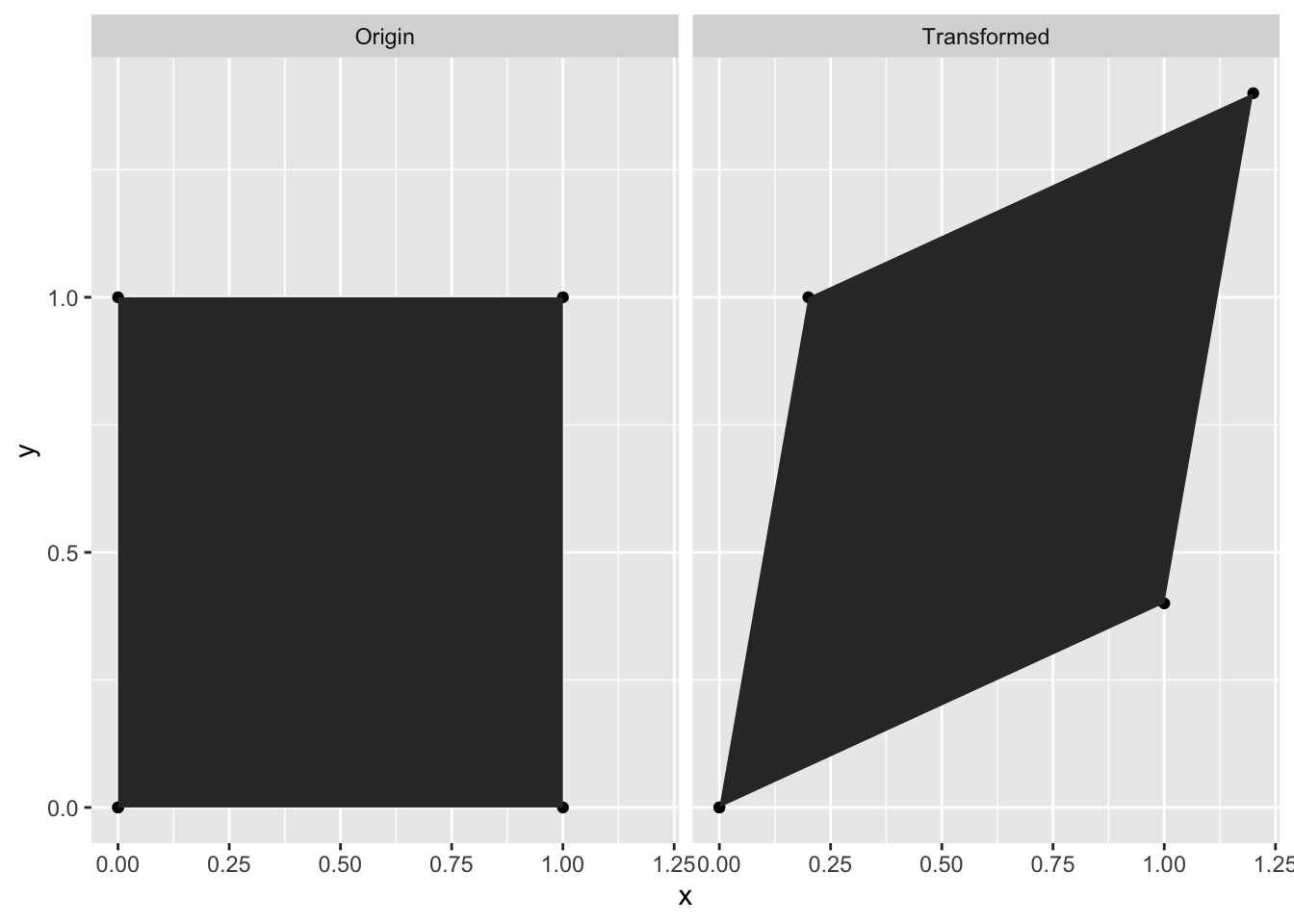

例えば，ここでは

\[\begin{align} \begin{pmatrix} 0.2 & 1.0 \\ 1.0 & 0.4 \end{pmatrix} \end{align}\]

変換後の平行四辺形の面積は\(|ad - bc| = 0.92\)となる．いま考えているもともとの重積分(2.1)の結果は1だったが，変数変換後の面積が一致していないことがわかる．そこで，変数変換した場合に，面積を補正するような操作が必要となる．

この場合においてのみ，\(1/|ad-bc|\)という補正をすれば良いことがわかる．

では一般の場合には補正項をどのようにすれば良いのかについて，次の定理が役に立つ．

Theorem 2.2 (ヤコビ行列) 二変数関数\(f(x,y)\)のある領域\(R\)上で重積分\(\displaystyle \int \int_R f(x,y) dxdy\)について，\(x = u(s,t), y = v(s,t)\)という変換を考える．ただし，この変換は逆変換が存在するものとする．このとき，

\[\begin{align} \frac{\partial (x,y)}{\partial (s,t)} = \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \\ \end{pmatrix} \end{align}\]

とする．この行列をヤコビ行列という．またこの行列の行列式をヤコビ行列式という．慣習的にヤコビ行列を\(J\)と表すことが多い．

いま，\((x,y)\)の領域を\(R\)，\((s,t)\)の領域を\(R'\)として

\[\begin{align} \int \int_R f(x,y) dxdy = \int \int_{R'} f(u(s,t), v(s,t))|J|^{-1}dsdt \end{align}\]

と表すことができる．ここで\(|J|\)はヤコビ行列の行列式である．

Example 2.2 (ヤコビ行列) \(f(x,y) = x + 2y, R = \{ (x,y) | 0 \leq x-y \leq 1, 0 \leq x+y \leq 1 \}\)として， \(f\)の\(R\)上での重積分を考える．ここで，\(s=x-y, t=x+y\)という変数変換をしてみると，\(R'=\{ (x,y) | 0\leq s\leq1, 0\leq t \leq1 \}\)上での重積分とすることができる．また，この変換について\(x = (s+t)/2, y=-(s-t)/2\)が成り立つ．

この変換は

\[\begin{align} \begin{pmatrix} s \\ t \end{pmatrix} = \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \end{align}\]

と表すことができる．またヤコビ行列は

\[\begin{align} J = \frac{\partial (s,t)}{\partial (x,y)} = \begin{pmatrix} \frac{\partial s}{\partial x} & \frac{\partial s}{\partial y} \\ \frac{\partial t}{\partial x} & \frac{\partial t}{\partial y} \end{pmatrix} = \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix} \end{align}\]

となりヤコビ行列の行列式\(|J|\)は\(2\)となる．従って変数変換後の積分は，

\[\begin{align} \int \int_R (x+2y) dxdy &= \int \int_{R'} \left( -\frac12 s + \frac32 t \right) 2^{-1} dsdt \\ &= \frac14 \end{align}\]

となる．このケースでは変数変換により，積分範囲が単純になっている．

Exercise 2.2 (ヤコビ行列) Example (2.2) について，積分を計算し答えが\(1/4\)となることを確かめよ．