1 積分
積分は主に関数と\(x\)軸で囲まれる領域の面積や,関数の累積量の計算に利用され,実用においては微分と並びとても重要な計算手法の一つである. 統計学においては,確率の計算のために用いられることが多い.後に紹介する確率密度関数は,全積分の結果が1であるという前提があり,確率計算を積分として行うことができるように設計されている.
1.1 原始関数
原始関数を微分の逆操作の結果として,以下のように定義する.
Definition 1.1 (原始関数) 関数\(f(x)\)の原始関数とは
\[\begin{align} F'(x) = f(x) \end{align}\]
となるような関数\(F(x)\)のことである.
微分においては,定数項の微分が\(0\)になることから,\(F'(x) + C\)と\(F'(x)\)という二つの関数の微分はどちらも\(f(x)\)となる. すなわち,原始関数\(F'(x)\)は定数項を考慮すれば無数に存在する.この微分操作によって無視できる定数項を積分定数(constant of integration)と呼ぶ. ゆえに,積分の結果を原始関数として表現する場合は原則として積分定数を明示する.慣習的にはConstantの頭文字をとって\(C\)として
\[ F'(x) + C, (C \text{ は積分定数}) \] などと表す.
微分の性質から直ちに原始関数について次の定理を得る.
Theorem 1.1 (原始関数の性質) 関数\(f(x), g(x)\)について,次が成り立つ.
- \(\int af(x)dx = a \int f(x)dx, (aは定数)\)
- \(\int (f(x) \pm g(x))dx = \int f(x)dx \pm \int g(x)dx\)
一般的な関数の微分の結果をまとめた表の対応として,原始関数をまとめた表を以下に示す(見やすさのため,ここでは積分定数は無視する).
\[ \begin{array}{c|ccccc} \hline f(x) & x^k (k \neq 1) & e^x & 1/x & a^x & {1 \over x \log a} \\ \hline \int f(x) dx & {1 \over k+1} x^{k+1} & e^x & \log x & {1 \over \log a} a^x & \log_a x \\ \hline \end{array} \] \[ \begin{array}{c|cccccc} \hline f(x) & \sin x & \cos x & 1/\cos^2 x & {1 \over \sqrt{1-x^2}} & {-1 \over \sqrt{1-x^2}} & {1 \over 1+x^2}\\ \hline \int f(x) dx & -\cos x & \sin x & \tan x & \sin^{-1} x & \cos x^{-1} & \tan x^{-1} \\ \hline \end{array} \]
Exercise 1.1 (不定積分) 以下の積分を計算せよ.
- \(\int 4 dx\)
- \(\int (3x^3 + 2x)dx\)
- \(\int (\sin x + \sqrt{3} \cos x + e^x)dx\)
1.2 定積分
定積分とは,積分の際に特定の範囲に限定して積分を求める演算である.
Definition 1.2 (定積分) 連続関数\(f(x)\)についての\(x \in [a,b], a<b\)での定積分とは,\(x=a\)から\(x=b\)の範囲で\(x\)軸と\(f(x)\)で囲まれた領域の面積のことを意味する. これを
\[\begin{align} \int_a^b f(x) dx \end{align}\]
と表し,定積分と呼ぶ.\(f(x)\)は被積分関数という.
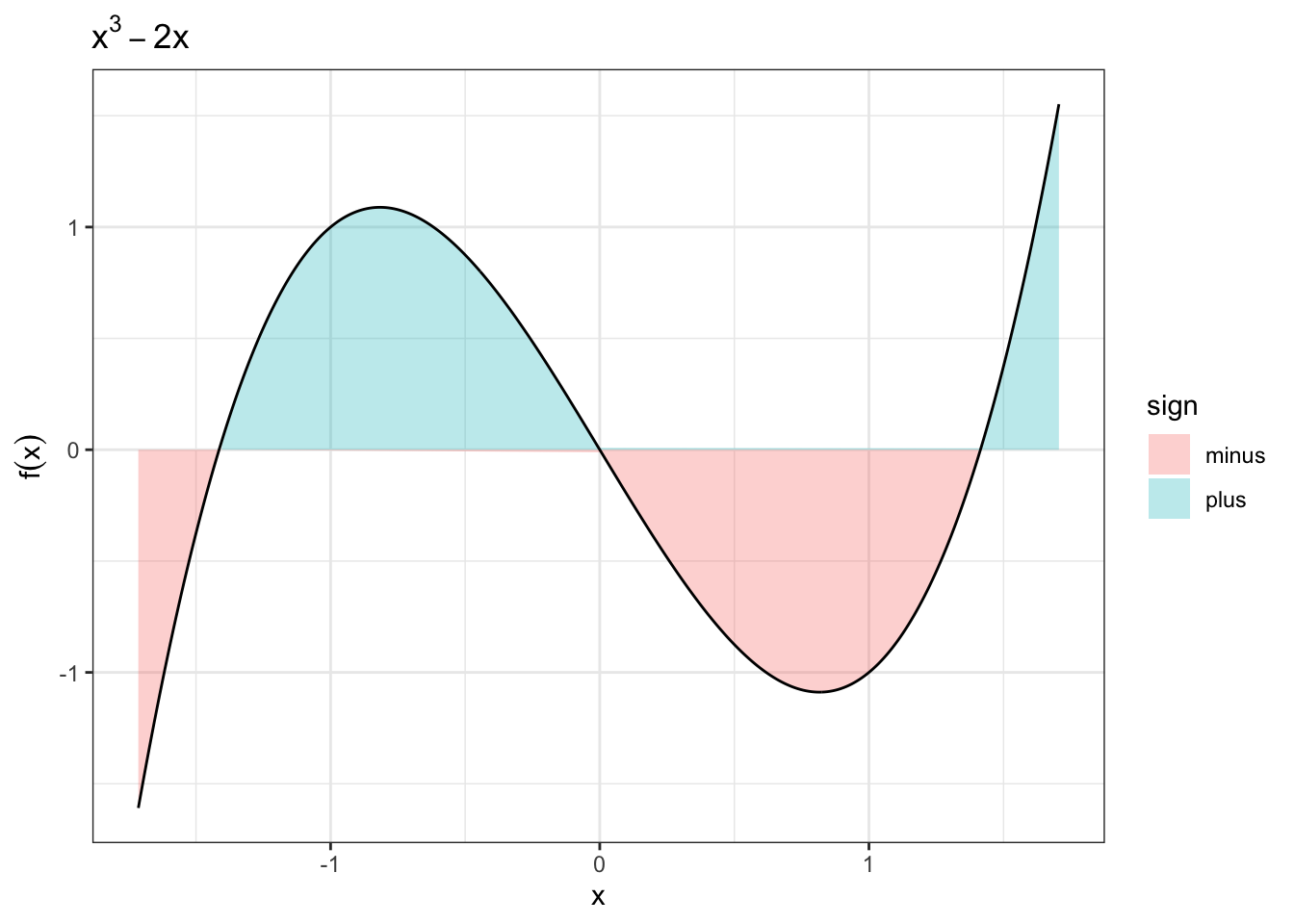
Figure 1.1: 定積分における面積の正負
定積分の計算では,面積の値が負になる場合がある.具体的には,関数値が\(x\)軸よりも上側(大きい)か,下側(小さい)かで別れる. 図1.1では青色の部分がプラスの面積,マイナスの面積であることを示している. そこで,我々が普段扱う面積と対応するように,負の面積についてのみ,ちゃんと正の値として足し上げる必要がある. そのためには,どの範囲で関数の値が負になるのかどうかについて,増減表などを用いてあらかじめ把握しておく必要がある.
また,不連続な点を有限個持つような関数\(f(x)\)における定積分は,連続な部分の定積分の和として定義される. 例えば\(I = [a,b]\)を定義域とし,ある点\(c \in (a,b)\)で不連続である関数\(f(x)\)については
\[ \int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx \] として定積分を求める.
Theorem 1.2 (定積分) 関数\(f(x)\)の原始関数を\(F(x)\)とする.このとき,\(f(x)\)の\(I = [a,b]\)での定積分は
\[\begin{align} \int_a^b f(x)dx = \left[ F(x) \right]_a^b = F(b) - F(a) \end{align}\]
と計算される.
Exercise 1.2 (定積分1) 次の定積分を求めよ.
\[\begin{align} \int_0^2 2e^xdx \end{align}\]
1.3 定積分の性質
ここでは,定積分のいくつかの性質について紹介する.
1.3.1 偶関数・奇関数
Theorem 1.3 (偶関数・奇関数の定積分) 関数\(f(x)\)が偶関数とする.すなわち,\(f(x) = f(-x)\)が成り立つとする.このとき, \[\begin{align} \int_{-a}^a f(x) dx = 2 \int_0^a f(x)dx \end{align}\] が成り立つ.
また,関数\(g(x)\)が奇関数,すなわち\(f(x) = -g(-x)\)が成り立つ時,
\[\begin{align} \int_{-a}^a g(x) dx = 0 \end{align}\]
が成り立つ.
偶関数とは,\(y\)軸に対して対称であるような関数で,奇関数は原点対称となるような関数である. これらは実際に可視化するとよりわかりやすい. ここでは,偶関数の例として\(x^2\)をみてみよう.なお,\(x^3 - 2x\)は奇関数であり(x^3と2xがそれぞれ奇関数であり,その和も奇関数となる), 図1.1がそのまま例となっている・
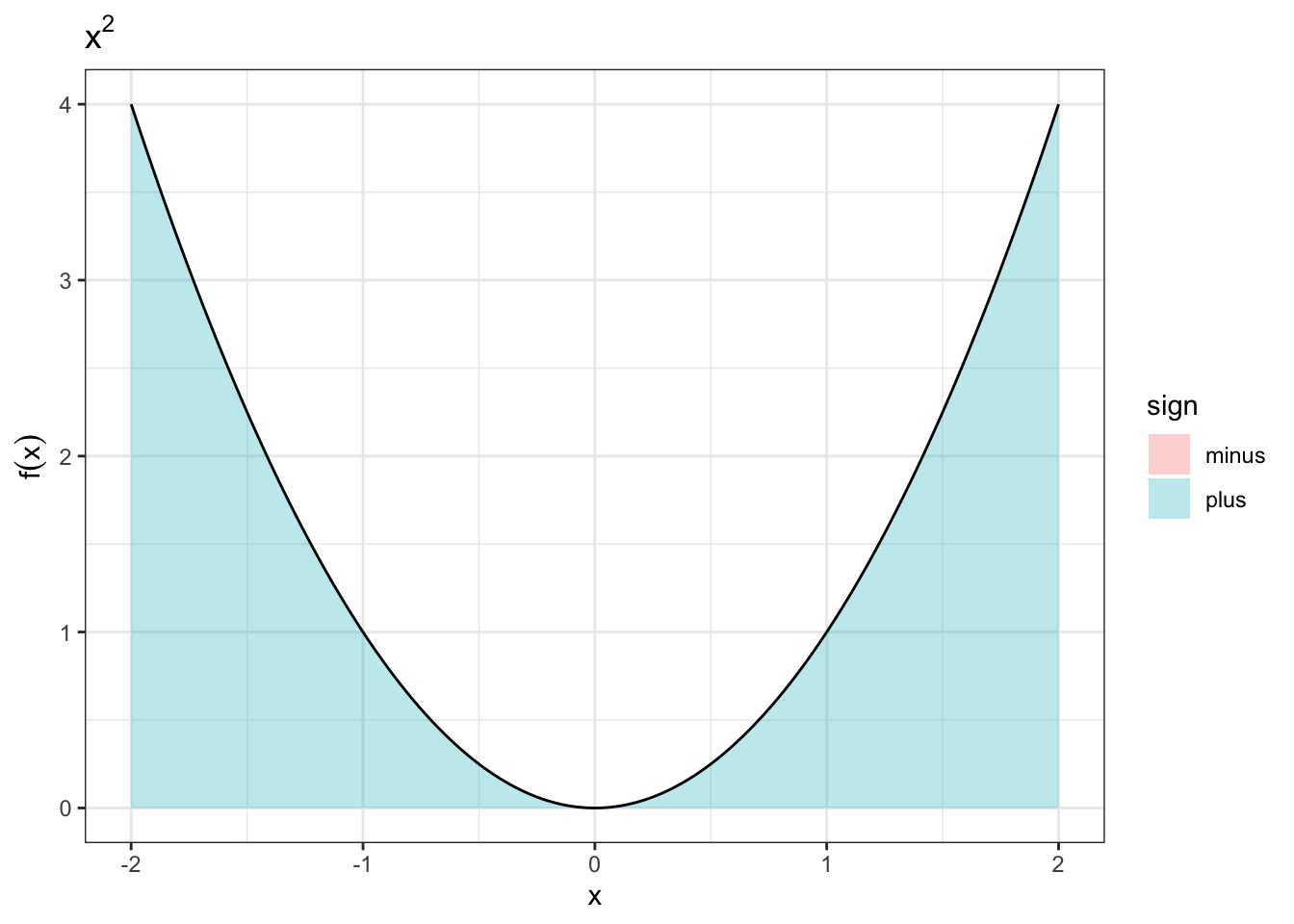
Figure 1.2: 偶関数の面積
図1.2は\(x^2\)の\([-2,2]\)でのグラフだが,\(y\)軸について対称であり,面積についても,\([-2,0]\)と\([0,2]\)が同じであることが視覚的にもわかるだろう. つまり,\([-2,2]\)の面積と\([0,2]\)の面積を2倍にしたものが一致するであろう,というのが定理の意味するところである. 逆に,奇関数は正負が逆転するため足し上げると0になる,ということである.
Theorem 1.4 (二つの関数で囲まれた領域の面積) 関数\(f,g\)に対して,区間\(I=[a,b]\)上で\(f(x) \geq g(x)\)が成り立つ時,
\[\begin{align} \int_a^b f(x) - g(x) dx \end{align}\]
は\(x=a, x=b, f(x), g(x)\)で囲まれた部分の面積を表す.
図1.3は,\(f(x) = e^x, g(x) = 2\sin(5x)\)とした時の,\([1,3]\)における面積を可視化したものである.見ての通りTheorem1.4の仮定を満たしており,面積をそのように求めることができる.
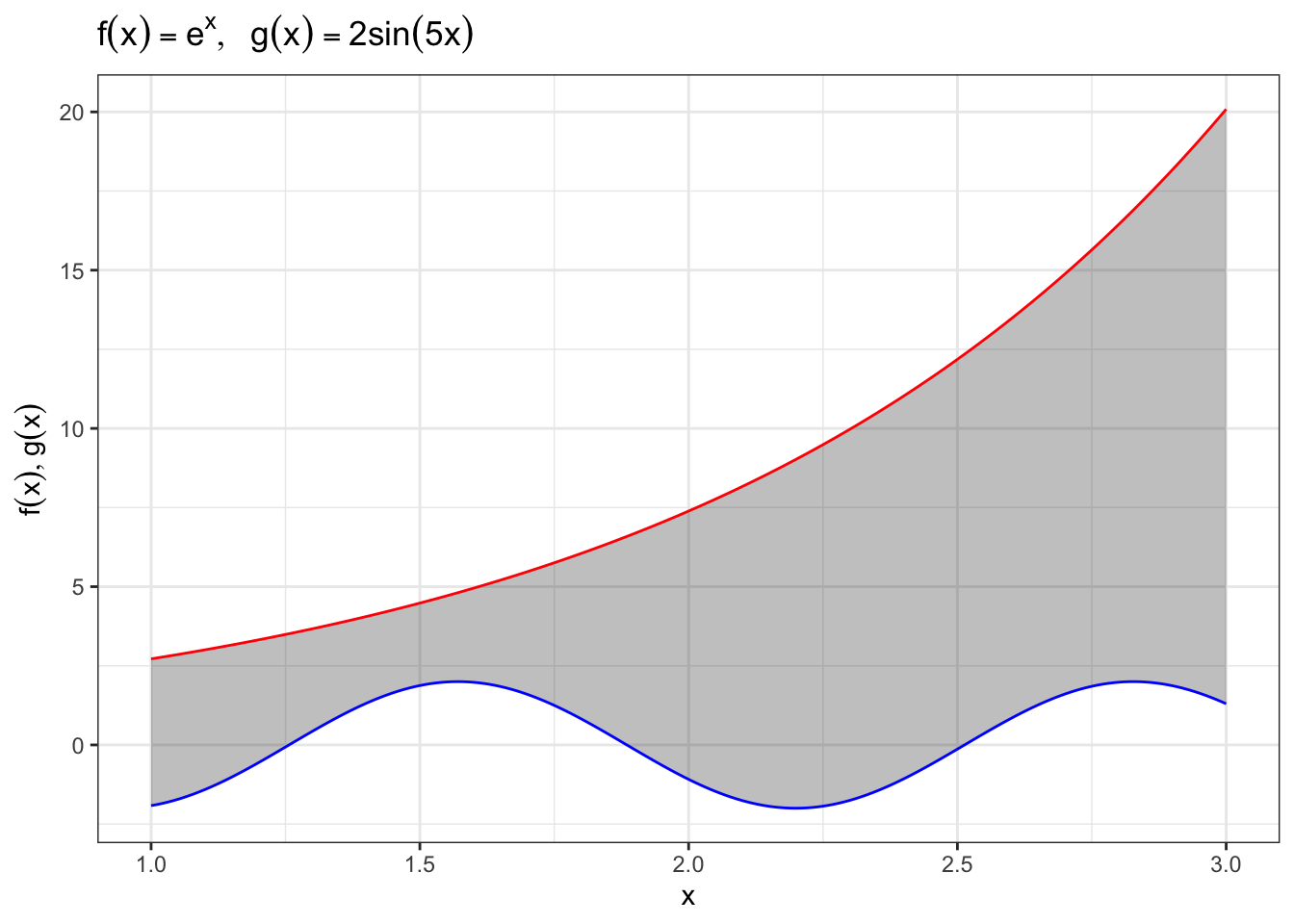
Figure 1.3: 二つの関数に囲まれた領域の面積
Theorem 1.1 (定積分の性質) 定積分について,次の3つの性質が成り立つ.
- 関数\(f(x)\)に対して,
\[\begin{align} \int_a^b f(x) dx + \int_b^c f(x) dx = \int_a^c f(x) dx \end{align}\]
が成り立つ.また,\(\int_a^a f(x) dx = 0\)より,\(\int_a^b f(x) dx = - \int_b^a f(x) dx\)となる.
- 関数\(f(x)\)に対して, \[\begin{align} \left| \int_a^b f(x) dx \right| \leq \int_a^b |f(x)| dx \end{align}\]
が成り立つ.
- 関数\(f(x)\)が区間\(I=[a,b]\)上で\(f(x) \geq 0\)とする.このとき
\[\begin{align} \int_a^b f(x) dx \geq 0 \end{align}\]
が成り立つ.もし関数\(f(x)\)が連続関数であれば,等号成立は\({}^{\forall}x \in I, f(x) = 0\)のときのみである.
また,関数\(f(x), g(x)\)が区間\(I\)上で\(f(x) \geq g(x)\)とすると,
\[\begin{align} \int_a^b f(x) dx \geq \int_a^b g(x) dx \end{align}\]
が成り立つ.\(f,g\)がともに連続関数の場合,等号成立は\({}^{\forall}x \in I, f(x) = g(x)\)のときのみである.
それぞれの証明は(椎名・姫野・保科 2019)を参照のこと.
Theorem 1.5 (リーマン和) 関数\(f(x)\)についての定積分\(\int_a^b f(x) dx\)は \[\begin{align} \int_a^b f(x) dx = \lim_{n \rightarrow \infty} \sum_{i=1}^{n} {b-a \over n} f \left( a + (b-a){i \over n} \right) \end{align}\] としても計算される.これをリーマン和とも呼ぶ.
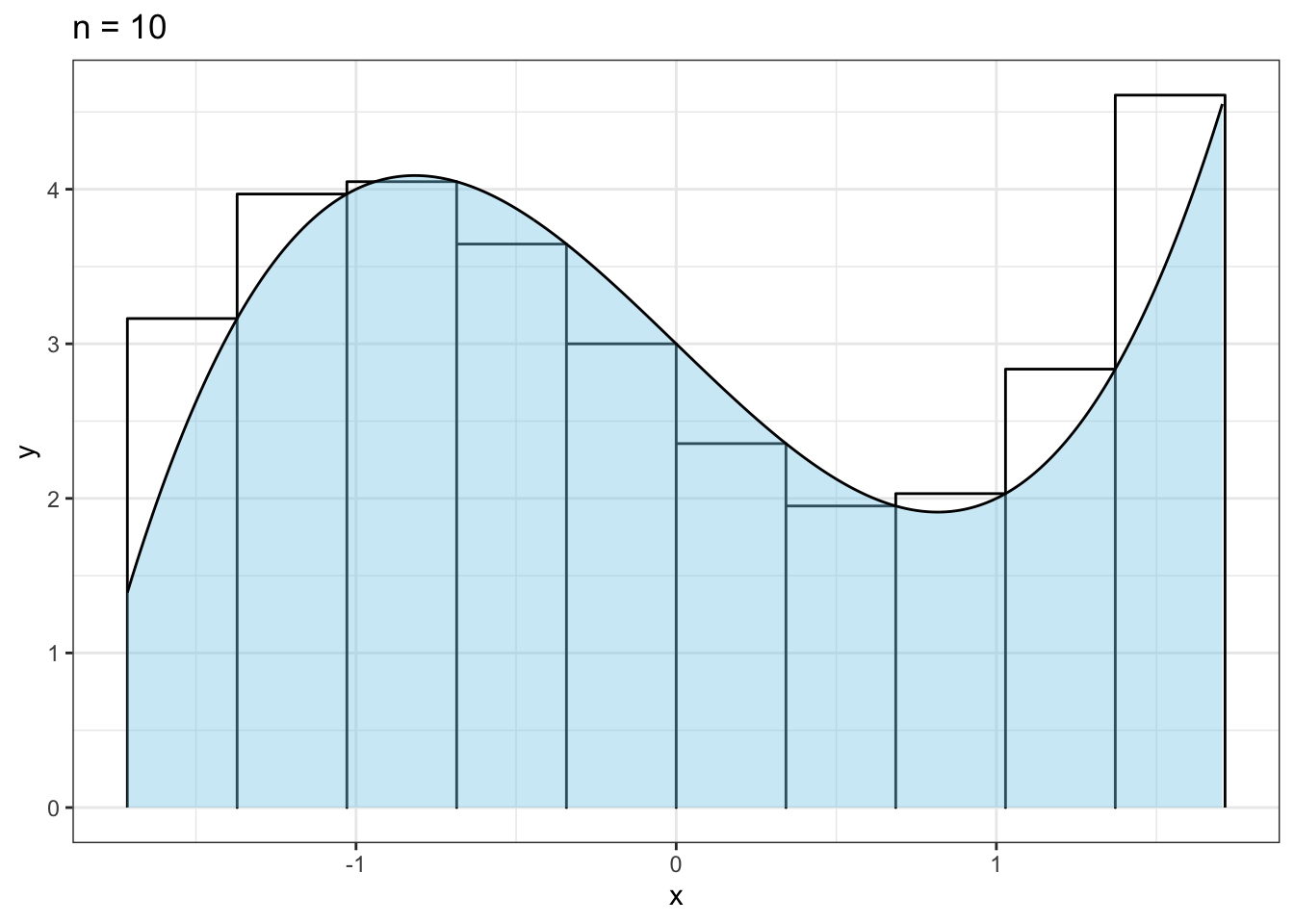
Figure 1.4: n=10の場合のリーマン和
Figure 1.4は\(f(x) = x^3 - 2x + 3\)の関数をリーマン和の考え方に従って\(n=10\)とした時の面積の近似である. このように,我々が求めやすい長方形を使って細かく分割して面積を足し上げると言うのが基本的な考え方である.
次に,この分割数\(n\)を大きくしていった時に,面積の近似がどの程度になるのかを可視化してみよう.
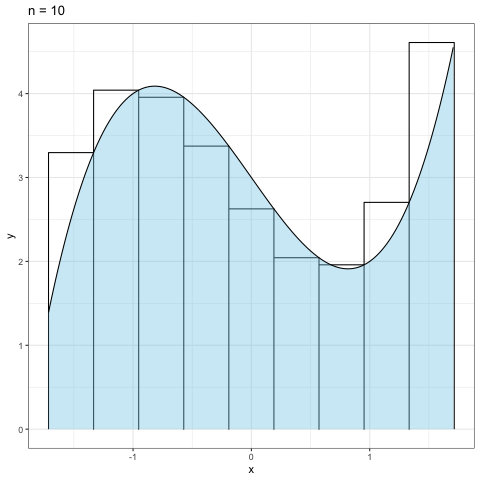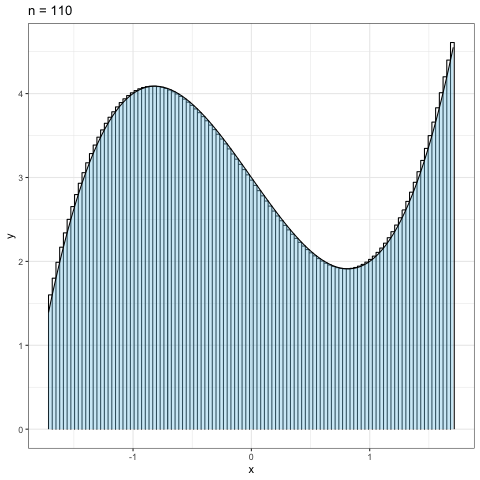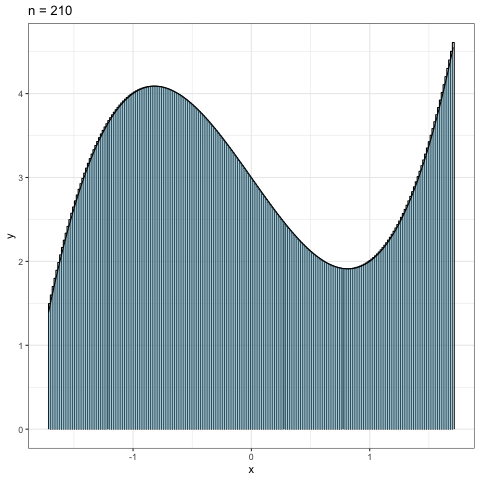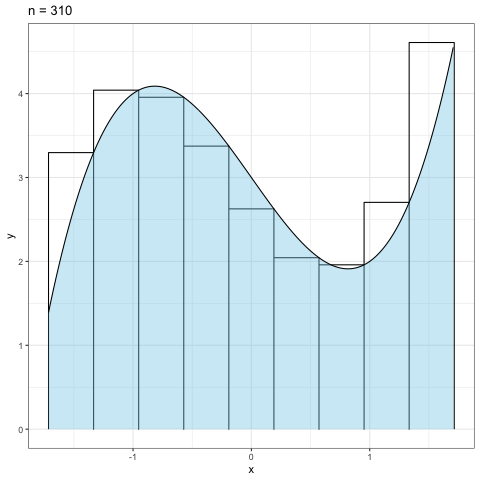
Figure 1.5: リーマン和のnを大きくしていった場合
図1.5は分割数の\(n\)を\(10\)から\(300\)まで10刻みで増やしていった時の 近似具合を見たものである.当然だが,分割数が大きくなればなるほど近似精度が高まっていくことが見て取れるだろう.
Exercise 1.3 (定積分2) 次の定積分を求めよ.
\[ \int_{-2}^{0} x^3 - 2x dx + \int_{0}^{2} x^3 - 2x dx \]
1.4 部分積分
より複雑な関数の積分を行う際によく用いられる方法として,部分積分と置換積分がある. ここではまず部分積分について紹介する.
Theorem 1.6 (部分積分) 関数\(F,g\)が区間\(I=(a,b)\)上で微分可能とし,\(F'(x) = f(x)\)とする.このとき,次が成り立つ. \[\begin{align} \int_a^b f(x) g(x) dx = \left[ F(x)g(x) \right]_a^b - \int_a^b F(x) g'(x) dx \end{align}\]
この式変形を部分積分と呼ぶ.
この定理は,微分の公式にある
\[ \left( f(x) g(x) \right)' = f'(x) g(x) + f(x) g'(x) \]
を両辺積分することによって直ちに導かれる. 部分積分を利用した計算例を見てみよう。
Example 1.1 (部分積分の例) \[\begin{align} \int_{0}^{2} x e^x dx &= \left[ x e^x \right]_0^2 - \int_{0}^{2} e^x dx \\ &= 2e^2 - \left[ e^x \right]_0^2 \\ &= 2e^2 - e^2 + 1 \\ &= e^2 + 1 \end{align}\]
Exercise 1.4 (部分積分) 次の定積分を求めよ. \[\begin{align} \int_1^2 \log x dx \end{align}\]
1.5 置換積分
次に部分積分と同様によく用いられるテクニックである置換積分について紹介する.
Theorem 1.7 (置換積分) 区間\(I=[a,b]\)で定義された関数\(f(x)\)の定積分を考える.このとき,関数\(g(t)\)が単調かつ,\(a=g(\alpha), b=g(\beta)\)とする. このとき,\(x=g(t)\)とすることで,次が成り立つ.
\[\begin{align} \int_a^b f(x) dx = \int_\alpha^\beta f(g(t)) {dx \over dt} dt = \int_\alpha^\beta f(g(t)) g'(t) dt \end{align}\]
一方,\(\int_a^b f(h(x)) dx\)に対して,\(t=h(x)\)という変換を行う場合は,
\[\begin{align} \int_a^b f(h(x))dx = \int_{h(b)}^{h(a)} f(t) {1 \over dt / dx} dt = \int_{}^{} f(t) {1 \over h'(h^{-1}(t))} dt \end{align}\]
となる.これらの式変形を置換積分という.
証明は(椎名・姫野・保科 2019)を参照のこと.
置換積分は,積分変数をある関数によって変換した先の空間で積分することを考えている. もし変換後の方が積分が求めやすければ問題なさそうであるが, 実際求めたいのはもとの空間での積分(面積)であるので,もともとの空間と置換した際の関数によって 写された先の空間の面積の関係を考慮しなければならない.その比率が\(dx/dt\)として表されているのである.
1.6 広義積分
次の図1.6のように,ある点だけ(ここでは\(x=0\))で定義されていない 関数について,その点を含む区間で積分を考えたい場合がある. このような時に広義積分が役に立つ.
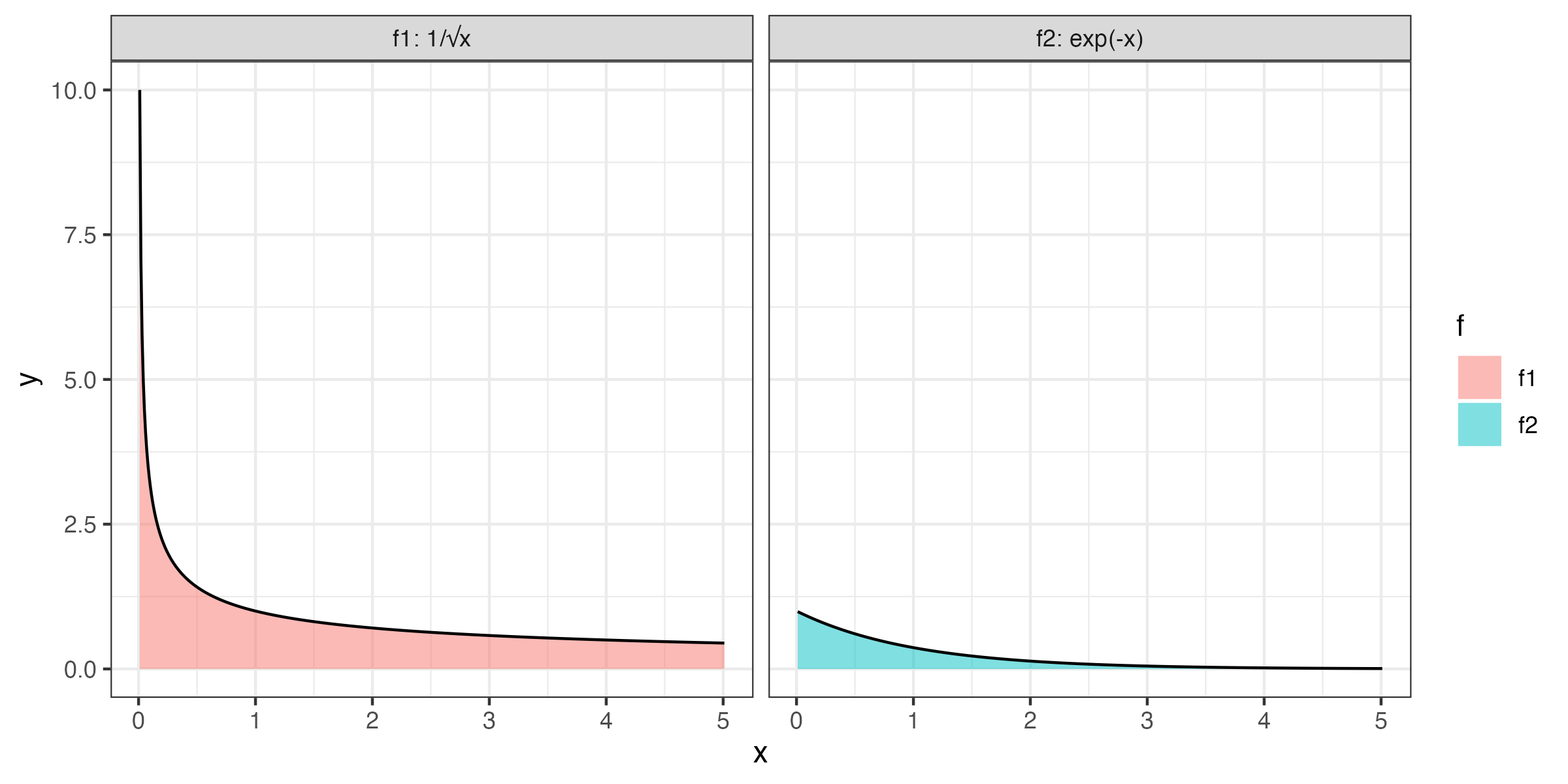
Figure 1.6: 広義積分の例
例えば,このよう場合,\(f(x) = 1/\sqrt{x}\)では\(x=0\)で有限な値を取らないし,\(f(x) = \exp(-x)\)では\(x \rightarrow \infty\)での定積分を計算する際は区間幅が無限大となってしまう.
Definition 1.3 (広義積分) 関数\(f\)の区間\(I = (a,b]\)上での定積分を考える.ただし,\(f(x)\)は\(x=a\)で定義されていないとする.ここで, \[\begin{align} \lim_{x \rightarrow a} \int_x^b f(t)dt \end{align}\] が存在する時,この極限を\(f(x)\)の\(x=a\)から\(x=b\)での広義積分と呼び, 通常の定積分と同様に\(\int_a^b f(x) dx\)と表す.また,関数\(f\)の区間\(I=[a, \infty)\)上での定積分については, \[\begin{align} \lim_{x \rightarrow \infty} \int_a^x f(t) dt \end{align}\]
が存在する時,この極限を\(f(x)\)の\(x=a\)から\(x=\infty\)での広義積分といい,\(\int_a^\infty f(x) dx\)と表す.
一つ広義積分の例を見てみよう.
Example 1.2 (広義積分の例) \[\begin{align} \int_0^2 {1 \over \sqrt{x}} dx &= \int_0^2 x^{-1/2} dx \\ &= \left[ 2 x^{1 \over 2} \right]_0^2 \\ &= 2\sqrt{2} \end{align}\]
ここで見たように実用上は,通常の定積分と同じように計算を進めれば良いが, その過程で広義積分となっているかどうかについてはしっかりと把握しているべきである.
Exercise 1.5 (広義積分) 次の関数を広義積分せよ. \[\begin{align} \int_0^\infty e^{-x} dx \end{align}\]