5 多変量の線形回帰モデル
単回帰モデルでは1つのの目的変数に対して1つの説明変数を扱なったが,目的変数に対して影響を及ぼしていると考えられる変数は唯一つとは限らない.単回帰モデルを拡張して複数の説明変数を考える線形回帰モデルを重回帰モデル(Multiple linear regression)と呼ぶ.またこれらを区別せずに単純に線形回帰モデルと呼ぶこともある.
すなわち,目的変数\(y_i\)に対して\(m\)個の説明変数\(x_i^{(1)}, x_i^{(2)}, \ldots, x_i^{(M)}\)を考えて次のように定式化したモデルである.
\[\begin{align} y_i &= \beta_0 + \beta_1 x_i^{(1)} + \beta_2 x_i^{(2)} + \cdots + \beta_m x_i^{(m)} + \varepsilon_i \\ &= \sum_{k=0}^{m} \beta_i x_i^{(k)} + \varepsilon_i \tag{5.1} \end{align}\]
ただし,$i = 1,2,,n \(,\)x_i^{(0)} = 1$とした.
偏回帰係数
重回帰モデルの場合,説明変数の種類\(m\)に対する回帰係数パラメーターを\(\beta_1,\beta_1, \ldots, \beta_m\)を偏回帰係数(partial regression coefficient)と呼び,これに切片項\(\beta_0\)を加えた計\(m+1\)個をまとめて回帰係数と呼ぶこともある.
ここで,先頭の要素に1でその後に各\(i\)における説明変数の値を要素にまとめたベクトル\(\boldsymbol x_i = (1, x_i^{(1)}, x_i^{(2)},\ldots,x_i^{(m)})\)を考えると(5.1)式は
\[\begin{align} y_i = \boldsymbol x_i^\top \boldsymbol \beta + \varepsilon_i \tag{5.2} \end{align}\]
と記述することができる.ただし\(\boldsymbol \beta = (\beta_0, \beta_1, \ldots, \beta_m)\)とした.
5.1 モデルの当てはめ
重回帰モデルの場合もRではlm関数によって次のように実行できる.
lm(説明変数 ~ 目的変数1 + 目的変数2 + ... + 目的変数m, data=データフレーム)本来データフレームの特定の列を呼び出す場合はdf$colとする必要があるが,data=dfと指定しておくと,列名をそのまま記述できる.
ここではalr4パッケージに入っているBGSgirlsというデータセットを例に重回帰モデルの当てはめを実行してみる.
まず,データセットの中身を簡単に確認しておく.また事前準備としてdf <- BGSgirlsとしてオブジェクト名をdfで使えるようにしておこう.
## 'data.frame': 70 obs. of 12 variables:
## $ WT2 : num 13.6 11.3 17 13.2 13.3 11.3 11.6 11.6 12.4 17 ...
## $ HT2 : num 87.7 90 89.6 90.3 89.4 85.5 90.2 82.2 85.6 97.3 ...
## $ WT9 : num 32.5 27.8 44.4 40.5 29.9 22.8 30 24.3 29.9 44.5 ...
## $ HT9 : num 133 135 142 137 136 ...
## $ LG9 : num 28.4 26.9 31.9 31.8 27.7 23.4 27.2 25.1 27.5 32.7 ...
## $ ST9 : int 74 65 104 79 83 60 67 44 76 81 ...
## $ WT18 : num 56.9 49.9 55.3 65.9 62.3 47.4 57.3 50 58.8 80.2 ...
## $ HT18 : num 159 166 162 168 171 ...
## $ LG18 : num 34.6 33.8 35.1 39.3 36.3 31.8 35 31.2 36.2 42.9 ...
## $ ST18 : int 143 117 143 148 152 126 134 77 118 135 ...
## $ BMI18: num 22.5 18.1 21 23.4 21.3 17.4 20.3 18.6 22 23.9 ...
## $ Soma : num 5 4 5.5 5.5 4.5 3 5 4 5 5.5 ...## WT2 HT2 WT9 HT9
## Min. :10.20 Min. :80.90 Min. :22.00 Min. :121.4
## 1st Qu.:11.80 1st Qu.:85.67 1st Qu.:27.62 1st Qu.:132.9
## Median :12.70 Median :87.10 Median :30.65 Median :135.7
## Mean :12.82 Mean :87.25 Mean :31.62 Mean :135.1
## 3rd Qu.:13.47 3rd Qu.:88.90 3rd Qu.:34.48 3rd Qu.:138.8
## Max. :17.00 Max. :97.30 Max. :47.40 Max. :152.5
## LG9 ST9 WT18 HT18
## Min. :22.60 Min. : 22.00 Min. :44.10 Min. :153.6
## 1st Qu.:26.30 1st Qu.: 51.25 1st Qu.:54.77 1st Qu.:163.0
## Median :27.45 Median : 59.00 Median :58.30 Median :166.8
## Mean :27.84 Mean : 60.46 Mean :59.78 Mean :166.5
## 3rd Qu.:29.25 3rd Qu.: 68.75 3rd Qu.:64.80 3rd Qu.:170.2
## Max. :32.70 Max. :107.00 Max. :97.70 Max. :183.2
## LG18 ST18 BMI18 Soma
## Min. :30.30 Min. : 77.0 Min. :17.40 Min. :3.000
## 1st Qu.:33.52 1st Qu.:114.5 1st Qu.:19.82 1st Qu.:4.000
## Median :34.85 Median :124.5 Median :21.05 Median :5.000
## Mean :35.42 Mean :124.7 Mean :21.53 Mean :4.779
## 3rd Qu.:37.08 3rd Qu.:135.0 3rd Qu.:22.48 3rd Qu.:5.000
## Max. :42.90 Max. :182.0 Max. :36.90 Max. :7.000それでは重回帰モデルの当てはめを実行する.ここではWT18をHT18, WT9で説明するモデルを作成することにする.
##
## Call:
## lm(formula = WT18 ~ HT18 + WT9, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.094 -3.185 -1.109 2.591 30.711
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -26.7286 20.5419 -1.301 0.1977
## HT18 0.3538 0.1321 2.678 0.0093 **
## WT9 0.8723 0.1378 6.330 2.35e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.032 on 67 degrees of freedom
## Multiple R-squared: 0.5294, Adjusted R-squared: 0.5153
## F-statistic: 37.68 on 2 and 67 DF, p-value: 1.083e-11説明変数を追加したい場合は+で繋いでいけば良い.またデータフレームに含まれる目的変数以外の全ての変数を説明変数としたい場合は.というワイルドカードを利用すると便利である.
##
## Call:
## lm(formula = WT18 ~ ., data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.57956 -0.24367 -0.01582 0.13246 1.77717
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.144e+02 2.403e+00 -47.595 <2e-16 ***
## WT2 4.684e-02 6.283e-02 0.745 0.4590
## HT2 -3.017e-02 2.877e-02 -1.048 0.2988
## WT9 1.035e-02 3.365e-02 0.307 0.7596
## HT9 -1.779e-02 3.015e-02 -0.590 0.5574
## LG9 -1.993e-02 7.735e-02 -0.258 0.7976
## ST9 6.428e-03 5.871e-03 1.095 0.2781
## HT18 7.092e-01 1.775e-02 39.969 <2e-16 ***
## LG18 1.069e-01 5.002e-02 2.137 0.0368 *
## ST18 -3.285e-03 4.014e-03 -0.818 0.4165
## BMI18 2.593e+00 4.371e-02 59.313 <2e-16 ***
## Soma 2.360e-01 1.306e-01 1.808 0.0759 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4377 on 58 degrees of freedom
## Multiple R-squared: 0.9979, Adjusted R-squared: 0.9974
## F-statistic: 2452 on 11 and 58 DF, p-value: < 2.2e-16.で全ての変数を指定してから,特定の変数を説明変数から取り除くこともできる.その場合は-で変数を繋げばよい.lm関数の中のモデル表現における-はその説明変数の値を引くのではなく取り除くことに注意されたい.
実際の関係性としてある説明変数の係数を-だと想定していたとしても,モデルの推定の結果\beta_jの値が負になれば良いし,どうしてもそのように表現したいという時は,あらかじめ説明変数の値を-1倍しておけば良い.
ただし,モデルの項としての足し引きについては本質的には推定される回帰係数によって決定されるものである.
5.2 説明変数の処理
ここでは基本的な説明変数の処理について紹介いこう.与えられたデータをそのまま使うのではなくモデルにとって有用な変数へと変化する作業を意味する.このような処理全般を特徴量生成と呼ぶこともある.
5.3 ダミー変数の作成
ダミー変数とは,質的データの値を数値に対応させるように変換した変数のことを意味する. 多くの場合はある値かどうかの\(1,0\)に変換する.
Rの基本的な演算操作で行う例を示そう.HT18という列の値に応じて新たなカテゴリを定義してそれらに該当するかどうかのダミー変数を作成する流れを紹介する.
5.3.1 自分で実装する
この処理を1から実装すると以下のようにできる.まず変換の定義として
\[ HT18cat = \begin{cases} low & HT18 < 160 \\ middle & 160 \leq HT18 < 170 \\ high & 170 \leq HT18 < 180 \\ very-high & 180 \leq HT18 \end{cases} \]
とすることにする. 次にある変数を受け取って上記のような値を返す関数を作成しておこう.
ht18_2_cat <- function(x){
res = c()
res[x < 160] <- "low"
res[{160 <= x} & {x < 170}] <- "middle"
res[{170 <= x} & {x < 180}] <- "high"
res[180 <= x] <- "very-high"
return(res)
}次にこの関数にHT19を適用する.
## [1] "low" "middle" "middle" "middle" "high" "middle"さらに,それぞれの値に対するダミー変数を作るには
- 要素数を行に,カテゴリ数を列に持つデータフレーム(マトリックス型でも良い)を作成
- 各列に1,0の値を埋める
ような操作が必要になる.具体的には以下のように処理することになる.
cat_2_dum <- function(x){
cat <- unique(x)
row_number <- length(x)
col_number <- length(unique(x))
res <- data.frame(matrix(0, nrow=row_number, ncol=col_number))
colnames(res) <- cat
for(i in 1:col_number){
ins <- ifelse(x == cat[i], 1, 0)
res[,cat[i]] <- ins
}
return(res)
}## low middle high very-high
## 1 1 0 0 0
## 2 0 1 0 0
## 3 0 1 0 0
## 4 0 1 0 0
## 5 0 0 1 0
## 6 0 1 0 05.3.2 パッケージを活用する:recipes
recipesというパッケージを利用します.インストールしていない人は以下を実行してください.
次にパッケージを読み込みます
df %>%
mutate(HT18cat = ht18_2_cat(HT18)) %>%
recipe(~HT18cat) %>%
step_dummy(HT18cat) %>% # dummy variable creation
prep() %>% # estimate
bake(new_data=NULL) %>%
head() # apply## # A tibble: 6 × 3
## HT18cat_low HT18cat_middle HT18cat_very.high
## <dbl> <dbl> <dbl>
## 1 1 0 0
## 2 0 1 0
## 3 0 1 0
## 4 0 1 0
## 5 0 0 0
## 6 0 1 0実は,ダミー変数はカテゴリ数から1引いた数があれば十分である,recipesを用いた例では上記のように3つの列が作成される.
5.5 日時に関する変数
2021-11-20 13:40:31のように年-月-日 時:分:秒の形式で表されるような日時データが与えられた時,それぞれのパートで分けた変数を新たな説明変数として加えることができる.
- 年
- 週数
- 月
- 曜日
- 週末か平日か
- 時
ここではこのような日付または時間のデータを操作するパッケージの紹介も兼ねて実装を紹介する.講義で配布するsample_timstamp.csvのデータセットをサンプルにみていこう.まずは読み込む.
## number_people date temperature
## 1 0 2016-06-24 10:04:26 57.05
## 2 32 2016-05-12 17:44:41 56.91
## 3 0 2016-05-21 07:40:34 54.53
## 4 10 2016-11-28 14:02:45 50.89
## 5 0 2016-05-27 11:28:46 54.73
## 6 31 2015-09-02 14:50:13 63.00date列にYYYY-mm-dd HH:MM:SSの形式で日時が記録されている.この文字列から上記のような変数を作成していく.
次にlubridateパッケージを読み込む.
後の流れはとても簡単で,
lubridateパッケージの関数群が扱えるオブジェクトに変換する
ymd()関数
lubridateパッケージが用意している関数を利用して変数を作成していく
詳細はこちらのドキュメントにまとまっているが,ほとんどの操作に必要な関数を提供してくれている.
早速ymd_hms()関数を使い,POSIXct, POSIXtといったRにおける時間を扱うクラスに変換しよう.
## [1] "2016-06-24 10:04:26 JST" "2016-05-12 17:44:41 JST"
## [3] "2016-05-21 07:40:34 JST" "2016-11-28 14:02:45 JST"
## [5] "2016-05-27 11:28:46 JST"デフォルトではタイムゾーンがUTCになっているが,日本時間で扱いたい場合はtz="Asia/Tokyo"という引数を指定する.
次に,各パートを取り出してみる.
## [1] 2016 2016 2016 2016 2016## [1] 26 19 21 48 22## [1] 6 5 5 11 5## [1] 6 5 7 2 6## [1] 1 0 1 0 1## [1] 24 12 21 28 27## [1] 10 17 7 14 11## [1] 4 44 40 2 28## [1] 26 41 34 45 46それでは最後にこれらの処理を活用してデータに変数を加える処理を実装する.
df %>%
mutate(ts = ymd_hms(date)) %>%
mutate(
year = year(ts),
month = month(ts),
week = week(ts),
day = day(ts),
wday = wday(ts),
is_weekends = ifelse(wday(ts)>5,1,0),
hour = hour(ts),
minute = minute(ts),
second = second(ts)
) %>% head()## number_people date temperature ts year month
## 1 0 2016-06-24 10:04:26 57.05 2016-06-24 10:04:26 2016 6
## 2 32 2016-05-12 17:44:41 56.91 2016-05-12 17:44:41 2016 5
## 3 0 2016-05-21 07:40:34 54.53 2016-05-21 07:40:34 2016 5
## 4 10 2016-11-28 14:02:45 50.89 2016-11-28 14:02:45 2016 11
## 5 0 2016-05-27 11:28:46 54.73 2016-05-27 11:28:46 2016 5
## 6 31 2015-09-02 14:50:13 63.00 2015-09-02 14:50:13 2015 9
## week day wday is_weekends hour minute second
## 1 26 24 6 1 10 4 26
## 2 19 12 5 0 17 44 41
## 3 21 21 7 1 7 40 34
## 4 48 28 2 0 14 2 45
## 5 22 27 6 1 11 28 46
## 6 35 2 4 0 14 50 13ここまで,日時型のデータから基本的な変数を作成する処理を見てきた.実際には,日本の祝日を考慮したい,など個別の要望が出てくることがあるが,その場合は祝日がいつなのかというマスター情報を作成してから判定することになるだろう.
5.6 集計値の特徴量化
例えば顧客の購買データを考える場合,特定のユーザーのデータは複数存在することがある.(同じ人が何度も買い物するなど).このような場合に,次のような集計値を新たな説明変数の候補に加えることができる.
- ユーザーの最もアクティブな時間帯はいつか
- 商品カテゴリごとの購入点数
- 商品カテゴリ・週数ごとにカウントを集計(どんな時期に買ったのか).
- 月ごとの購入金額の平均
ここについては実装の紹介については割愛する.
5.7 高次・交互作用
これは質的・量的変数問わず行える変換で,ある二つの変数\(\boldsymbol x_1 = (x_{1i}, x_{2i}, \ldots, x_{ni})^\top, \boldsymbol x_2 = (x_{2i}, x_{2i}, \ldots, x_{ni})^\top\)があった場合に次のような変数を新たに加えることができる.
- \(x_{1i} \times x_{2i}\)
- \(x_{1i}^{2}\)
- \(x_{2i}^{2}\)
これは2乗までのオーダーでの例だが,3乗でも良いし,2乗ともう一方を乗ずるような処理も行うことはできる.
このような変数を組み込んだ回帰モデルは多項式回帰モデルと呼ぶ.
\[\begin{align} y_i = \beta_0 + \beta_1 x_i + \beta_2 x_i^2 + \cdots + \beta_d x_i^d + \varepsilon_i' \end{align}\]
と表せるモデルである.
こちらの処理についてはlm()関数にモデルを記述する際に実行できるので比較的簡単で.改めてBGSgirlsのデータセットを例に実装を紹介しよう.
以下では3次の項までを考慮している.
##
## Call:
## lm(formula = WT18 ~ poly(HT18, degree = 3, raw = TRUE), data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.959 -5.198 -1.325 3.551 39.647
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -9.117e+03 9.726e+03 -0.937 0.352
## poly(HT18, degree = 3, raw = TRUE)1 1.620e+02 1.743e+02 0.930 0.356
## poly(HT18, degree = 3, raw = TRUE)2 -9.559e-01 1.040e+00 -0.919 0.361
## poly(HT18, degree = 3, raw = TRUE)3 1.886e-03 2.065e-03 0.913 0.365
##
## Residual standard error: 7.625 on 66 degrees of freedom
## Multiple R-squared: 0.2591, Adjusted R-squared: 0.2254
## F-statistic: 7.692 on 3 and 66 DF, p-value: 0.0001751poly(HT18, degree = 3, raw = TRUE)1というのが1次の項で末尾の数値が次数に対応している.以前の回帰モデルの推定結果と比較すると,この例はあまり効果的な特徴量ではなさそうということが分かる.
5.8 標準化
重回帰モデルでは複数の説明変数を扱うが,各変数の絶対値の差がありすぎると適切な影響を考慮できない場合がある.そのため,各変数の平均を0,分散を1にするように変換した方が良い結果が得られる場合がある.この変換を標準化と呼ぶ.具体的には\(\bar x\)を変数の平均,\(\sigma_x\)を変数の標準偏差として
\[ x'_i = \frac{x_i - \bar x}{\sigma_x} \]
という変換を施す.こうすると,平均が0で分散が1になる.実際にHT18の変数で試してみよう.
## [1] -1.25834221 -0.08959603 -0.71512216 0.20670581 0.71700344 -0.27066939元々の値とは異なり,0付近にデータが集まる.さらに平均と分散が期待したようになっているかも確認しよう.
## [1] 1.133955e-15## [1] 15.9 変数選択
重回帰モデルでは複数の変数を考慮することができるが,一方でどの変数をモデルに組み込むべきなのかを判断しなければいけないという問題が発生する.そこで,赤池情報量規準:AICと呼ばれる量を用いる方法を紹介する.
5.9.1 AIC:赤池情報量基準
AICは標本サイズを\(n\),モデルのパラメータ数を\(d\)として次のように定義される量でる.
\[ {\rm AIC} = n \log \left( \frac{\sum e_i^2}{n} \right) + n + 2 \times d \]
AICではその値がより小さいモデルを良いモデルだと考えられる.
RではAICを求めるにはAIC()関数を利用することで簡単に計算することができる.
これまでに使った2つのモデルを比較してみよう.
df <- BGSgirls
fit1 <- lm(WT18 ~ HT18 + WT9, data=df)
fit2 <- lm(WT18 ~ poly(HT18, degree=3, raw=TRUE), data=df)
print(c(AIC(fit1), AIC(fit2)))## [1] 455.1677 488.9366AICにおいてはfit1の方が良いモデルであると判断できる.変数の数がある程度多い場合はstep()関数を利用するとある程度自動的にモデル選択を行うことができる.
ここではBGSgirlsの変数全てを入れたモデルから始めた変数選択を実行してみよう.
## Start: AIC=-104.83
## WT18 ~ WT2 + HT2 + WT9 + HT9 + LG9 + ST9 + HT18 + LG18 + ST18 +
## BMI18 + Soma
##
## Df Sum of Sq RSS AIC
## - LG9 1 0.01 11.13 -106.75
## - WT9 1 0.02 11.13 -106.72
## - HT9 1 0.07 11.18 -106.41
## - WT2 1 0.11 11.22 -106.16
## - ST18 1 0.13 11.24 -106.03
## - HT2 1 0.21 11.32 -105.52
## - ST9 1 0.23 11.34 -105.40
## <none> 11.11 -104.83
## - Soma 1 0.63 11.74 -102.99
## - LG18 1 0.88 11.99 -101.52
## - HT18 1 306.07 317.18 127.77
## - BMI18 1 674.03 685.14 181.68
##
## Step: AIC=-106.75
## WT18 ~ WT2 + HT2 + WT9 + HT9 + ST9 + HT18 + LG18 + ST18 + BMI18 +
## Soma
##
## Df Sum of Sq RSS AIC
## - WT9 1 0.01 11.13 -108.71
## - HT9 1 0.06 11.18 -108.40
## - WT2 1 0.10 11.22 -108.15
## - ST18 1 0.13 11.26 -107.92
## - ST9 1 0.22 11.35 -107.35
## - HT2 1 0.22 11.35 -107.35
## <none> 11.13 -106.75
## - Soma 1 0.63 11.75 -104.92
## - LG18 1 1.44 12.56 -100.25
## - HT18 1 308.63 319.76 126.33
## - BMI18 1 722.57 733.70 184.47
##
## Step: AIC=-108.71
## WT18 ~ WT2 + HT2 + HT9 + ST9 + HT18 + LG18 + ST18 + BMI18 + Soma
##
## Df Sum of Sq RSS AIC
## - HT9 1 0.05 11.18 -110.38
## - ST18 1 0.13 11.26 -109.91
## - WT2 1 0.17 11.30 -109.64
## - ST9 1 0.22 11.35 -109.35
## - HT2 1 0.24 11.37 -109.25
## <none> 11.13 -108.71
## - Soma 1 0.79 11.92 -105.89
## - LG18 1 1.60 12.73 -101.31
## - HT18 1 335.26 346.39 129.94
## - BMI18 1 726.69 737.83 182.87
##
## Step: AIC=-110.38
## WT18 ~ WT2 + HT2 + ST9 + HT18 + LG18 + ST18 + BMI18 + Soma
##
## Df Sum of Sq RSS AIC
## - ST18 1 0.12 11.30 -111.66
## - ST9 1 0.17 11.35 -111.35
## - WT2 1 0.17 11.35 -111.32
## <none> 11.18 -110.38
## - HT2 1 0.42 11.60 -109.80
## - Soma 1 0.74 11.93 -107.87
## - LG18 1 1.60 12.78 -103.02
## - HT18 1 641.84 653.03 172.32
## - BMI18 1 740.66 751.84 182.18
##
## Step: AIC=-111.66
## WT18 ~ WT2 + HT2 + ST9 + HT18 + LG18 + BMI18 + Soma
##
## Df Sum of Sq RSS AIC
## - ST9 1 0.07 11.37 -113.21
## - WT2 1 0.20 11.50 -112.45
## <none> 11.30 -111.66
## - HT2 1 0.47 11.77 -110.79
## - Soma 1 0.88 12.18 -108.41
## - LG18 1 1.52 12.82 -104.81
## - HT18 1 643.71 655.01 170.53
## - BMI18 1 746.05 757.35 180.69
##
## Step: AIC=-113.21
## WT18 ~ WT2 + HT2 + HT18 + LG18 + BMI18 + Soma
##
## Df Sum of Sq RSS AIC
## - WT2 1 0.31 11.69 -113.31
## <none> 11.37 -113.21
## - HT2 1 0.50 11.87 -112.21
## - Soma 1 0.93 12.31 -109.68
## - LG18 1 1.84 13.21 -104.71
## - HT18 1 655.08 666.45 169.74
## - BMI18 1 788.77 800.15 182.54
##
## Step: AIC=-113.31
## WT18 ~ HT2 + HT18 + LG18 + BMI18 + Soma
##
## Df Sum of Sq RSS AIC
## - HT2 1 0.23 11.92 -113.94
## <none> 11.69 -113.31
## - Soma 1 1.31 13.00 -107.85
## - LG18 1 1.73 13.41 -105.65
## - HT18 1 658.68 670.37 168.15
## - BMI18 1 788.46 800.15 180.54
##
## Step: AIC=-113.95
## WT18 ~ HT18 + LG18 + BMI18 + Soma
##
## Df Sum of Sq RSS AIC
## <none> 11.92 -113.94
## - Soma 1 1.31 13.23 -108.64
## - LG18 1 1.58 13.50 -107.21
## - BMI18 1 792.14 804.06 178.88
## - HT18 1 999.52 1011.44 194.94結果としてはAICの意味で,以下のモデルが最良であるという結果を得ることができた.
##
## Call:
## lm(formula = WT18 ~ HT18 + LG18 + BMI18 + Soma, data = df)
##
## Coefficients:
## (Intercept) HT18 LG18 BMI18 Soma
## -116.6196 0.6969 0.0935 2.5837 0.2929##
## Call:
## lm(formula = WT18 ~ HT18 + LG18 + BMI18 + Soma, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.78861 -0.28065 -0.03814 0.17082 1.78220
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.166e+02 1.471e+00 -79.255 < 2e-16 ***
## HT18 6.969e-01 9.437e-03 73.841 < 2e-16 ***
## LG18 9.350e-02 3.180e-02 2.940 0.00454 **
## BMI18 2.584e+00 3.930e-02 65.736 < 2e-16 ***
## Soma 2.929e-01 1.095e-01 2.675 0.00945 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4282 on 65 degrees of freedom
## Multiple R-squared: 0.9977, Adjusted R-squared: 0.9976
## F-statistic: 7047 on 4 and 65 DF, p-value: < 2.2e-16## [1] 86.70605決定係数は0.99でAICは86という結果になっている.このようにプログラムによってある程度自動化することはできるが,あまりに良すぎる結果が出る場合は,そもそも説明変数に実質目的変数変そのものであるような変数紛れ込んでいる場合がるので注意が必要である. そのため,モデル選択はいろいろな観点から見て,慎重に行うべきである. また,上記のような状態を「リークしている」と言うこともある.
この例では以下のように,WT18とBMI18がほぼ線形の関係にあるため,この影響が強いと考えられる..
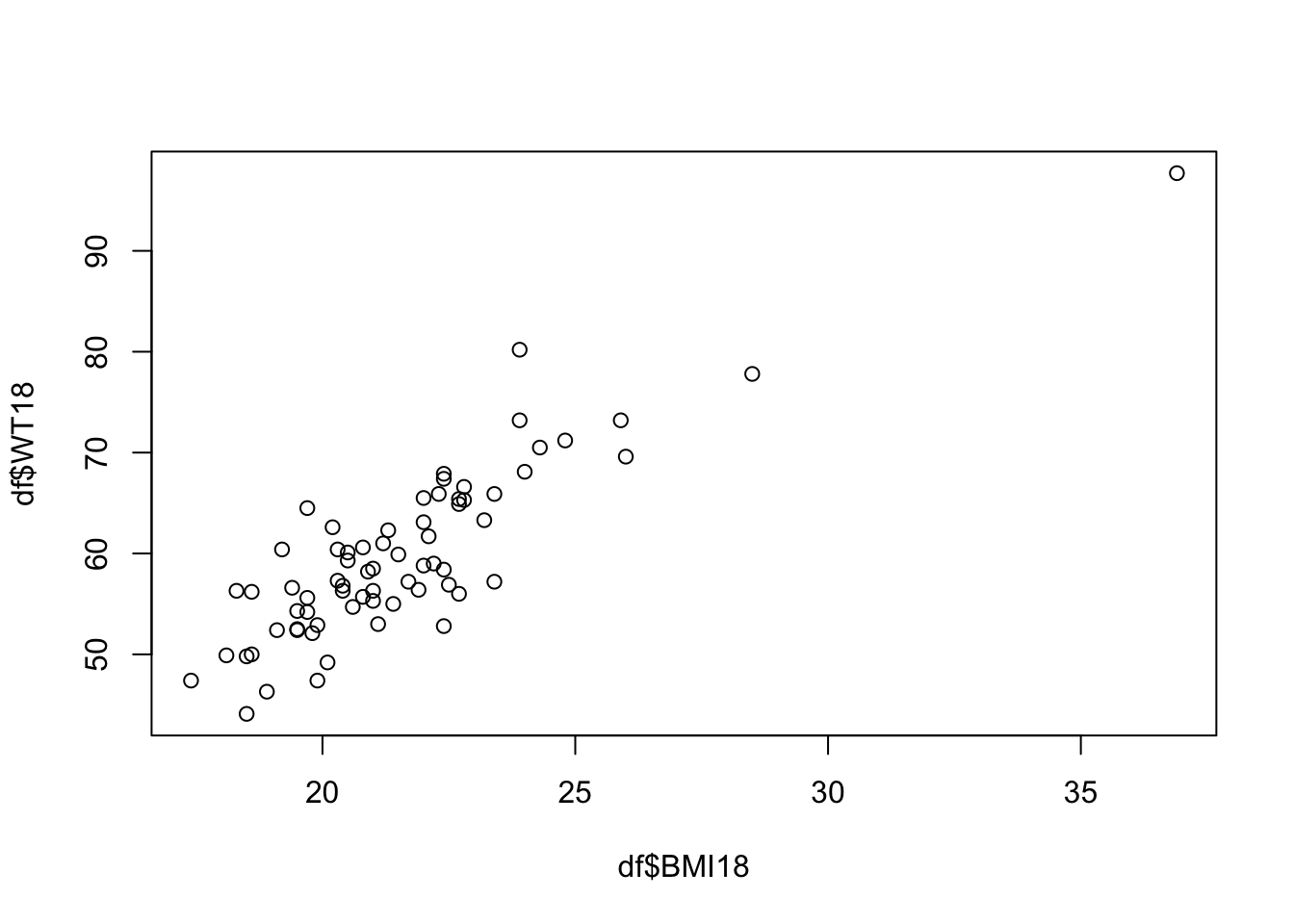
?BSGgirlsを実行してヘルプを見てみると,
WT18:Age 18 weight(kg)BMI18:Body Mass Index.WT18 / (HT18/100)^2
と定義されていて,そもそもBMI18の計算にWT18が利用されているため,ほとんどリークしているといっても良いだろう.
5.10 パラメータの推定値と信頼区間
モデルの学習した結果得られるパラメータの推定値とその関連指標について紹介していこう.
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -116.61960907 1.471445989 -79.255107 2.155689e-66
## HT18 0.69686370 0.009437403 73.840622 2.039516e-64
## LG18 0.09349889 0.031803392 2.939903 4.542296e-03
## BMI18 2.58367275 0.039304011 65.735601 3.538889e-61
## Soma 0.29292748 0.109514675 2.674778 9.449443e-035.10.1 信頼区間
パラメータの推定値は真の値かどうかは定かでは無く,あくまで最も良いだろうという値に過ぎない.そこで,信頼区間という概念が導入される.これは,パラメータを1点で推定するのでは無くある程度の幅を持たせて推定しようという試みでもある.具体的にはXX%の確率で真の値を含むと考えられる区間を意味している.(信頼区間の中に必ず真の値があるとは限らないことに注意して欲しい).
信頼区間はStd. Errorの値を利用して計算される(詳細はRによる統計的データ解析4章を参照されたい).
R上ではconfint()関数を利用すればよい.
## 2.5 % 97.5 %
## (Intercept) -119.55828964 -113.6809285
## HT18 0.67801590 0.7157115
## LG18 0.02998313 0.1570147
## BMI18 2.50517722 2.6621683
## Soma 0.07421157 0.5116434デフォルトでは95%信頼区間が計算されるが,level引数の値を変えることで変更することも可能である.
## 5 % 95 %
## (Intercept) -119.07491679 -114.1643014
## HT18 0.68111611 0.7126113
## LG18 0.04043061 0.1465672
## BMI18 2.51808867 2.6492568
## Soma 0.11018735 0.47566765.10.2 仮説検定
重回帰モデルの仮説検定では,各々のパラメータ\(\hat \beta_i\)に対して
- 帰無仮説\(H_0:\beta_i = 0\)
- 対立仮説\(H_1:\beta_i \neq 0\)
という二つの仮説を考え,帰無仮説\(H_0\)を棄却できるのかどうかを検討する. これは,ある説明変数が目的変数に何ら影響がないことを確かめているとも取れる. 実際,もし\(\beta_i = 0\)であればモデル上その項は無いものと同じである. (数理的な部分についての詳細はRによる統計的データ解析を参照されたい)
大まかに帰無仮説を棄却すべきかどうかの判断材料はPr(>|t|)という部分の数値を用いることが多い.このPr(>|t|)の値は回帰係数のP値と呼ばれるものにあたる.
これは帰無仮説\(H_0:\beta_i = 0\)が正しいと仮定した時,\(\beta_i\)が従うべき確率分布に対して,
推定された\(\hat \beta_i\)が得られる確率を意味している.
すなわちP値が十分に小さければ,そもそも仮定が間違っているのだと判断する根拠として使えるだろうということである.これを帰無仮説を棄却する,と表現する.
具体的にはP値を\(0.01, 0.05, 0.03\)という閾値以下であれば帰無仮説を棄却するというような運用が見られる.
また,そもそも信頼区間に\(0\)を含むような場合は帰無仮説が\(H_0\)棄却できていないとも考えられる.ここは注意するポイントの一つである.
また,最も注意すべき点は,帰無仮説を棄却できると判断するのはあくまで分析者の主観であるということである..得られたモデルが線形回帰以外を含む他のどんなモデルよりも精度が良く,しかも真のモデルそのものであるという保証はどこにも無いのである.
##
## Call:
## lm(formula = WT18 ~ HT18 + LG18 + BMI18 + Soma, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.78861 -0.28065 -0.03814 0.17082 1.78220
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.166e+02 1.471e+00 -79.255 < 2e-16 ***
## HT18 6.969e-01 9.437e-03 73.841 < 2e-16 ***
## LG18 9.350e-02 3.180e-02 2.940 0.00454 **
## BMI18 2.584e+00 3.930e-02 65.736 < 2e-16 ***
## Soma 2.929e-01 1.095e-01 2.675 0.00945 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.4282 on 65 degrees of freedom
## Multiple R-squared: 0.9977, Adjusted R-squared: 0.9976
## F-statistic: 7047 on 4 and 65 DF, p-value: < 2.2e-165.11 発展的な回帰モデル
最後に,線形回帰モデルの発展系のモデルを紹介しよう. ここで紹介するリッジ回帰・ラッソ回帰・エラスティックネットの3種類は モデルの構造そのものは線形回帰モデルだが,パラメータを推定する際の条件に手を加えたものである.
5.12 リッジ回帰
リッジ回帰は残差を最小化するだけでは無く,パラメータの絶対値の大きさにもペナルティーを科しながら推定を行う. 具体的には
\[\begin{align} \min_{\{\beta_j\}_{j=0}^{m}} \sum_{i=1}^n (y_i - \boldsymbol x^\top \boldsymbol \beta)^2 + \lambda \sum_{j=1}^{m} \beta_j^2 \tag{5.3} \end{align}\]
という条件を科します.\(\lambda\)は正則化パラメーター・罰則パラメーターとも呼ばれ,分析者で主観的に決めるかクロスバリデーションという手法を使って手続き的に決めることもできる.直感的には,パラメータが大きくなるのを防ぐように推定をする.
5.12.1 多重共線性
説明変数の間に強い相関が存在する場合,パラメータの推定に悪影響を及ぼすことが知られている.このような状態を多重共線性を持つと言う. Rによるデータ解析入門で紹介されている例を使って見ていこう.
まずは相関がとても強い3つの変数を用意してみる.
## [1] 0.9998099## [1] 0.9998121次に,x1, x2とx1, x3というペアで説明変数を加えた2つのモデルを学習してみよう.
##
## Call:
## lm(formula = y ~ x1 + x2)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.166 -4.417 -1.206 2.764 40.642
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -59.844 25.474 -2.349 0.0218 *
## x1 -1.925 7.742 -0.249 0.8044
## x2 2.643 7.764 0.340 0.7346
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.618 on 67 degrees of freedom
## Multiple R-squared: 0.2492, Adjusted R-squared: 0.2268
## F-statistic: 11.12 on 2 and 67 DF, p-value: 6.751e-05##
## Call:
## lm(formula = y ~ x1 + x3)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.166 -4.417 -1.206 2.764 40.642
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -59.844 25.474 -2.349 0.0218 *
## x1 3.361 7.789 0.431 0.6675
## x3 -2.643 7.764 -0.340 0.7346
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.618 on 67 degrees of freedom
## Multiple R-squared: 0.2492, Adjusted R-squared: 0.2268
## F-statistic: 11.12 on 2 and 67 DF, p-value: 6.751e-05これらのモデルを見ると,いずれの回帰係数も帰無仮説を棄却できるほどP値が低く無いことがわかる.
しかも,同じx1の変数に対する推定値の正負が逆転している.
多重共線性を持つ場合はこのように推定値の絶対値が大きくなり挙動が不安定になるという状況になる.
この時に推定を安定化させることができるのがリッジ回帰の特徴であり,これをもたらしているのが,推定の際にパラメータの絶対値の大きさにペナルティを科すという部分である.
5.12.2 リッジ回帰の実行
それではモデルを学習させてみよう.そのためにはglmnetパッケージが必要になるので以下を実行する.
ライブラリを読み込み,実行する.
cv.glmnet()関数はクロスバリデーションという手法によって適切に\(\lambda\)の値を決定して推定値を求めてくれる.
##
## Call: cv.glmnet(x = x, y = y, alpha = 0)
##
## Measure: Mean-Squared Error
##
## Lambda Index Measure SE Nonzero
## min 0 100 58.98 24.86 2
## 1se 4288 1 77.32 21.38 2推定された値はcoef関数で得ることができる.
## 3 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) -55.8898683
## x1 0.3417724
## x2 0.35275235.13 ラッソ回帰
ラッソ回帰はリッジ回帰とよく似ているが最小化する際のパラメータの制約が少し異なる形をしている.具体的には
\[\begin{align} \min_{\{\beta_j\}_{j=0}^{m}} \sum_{i=1}^n (y_i - \boldsymbol x^\top \boldsymbol \beta)^2 + \lambda \sum_{j=1}^{m} |\beta_j| \tag{5.4} \end{align}\]
となっている.
リッジ回帰では回帰係数\(\beta_j\)の二乗和に制約を科すが,Lasso回帰では回帰係数\(\beta_j\)の絶対値の和に制約を科す. ラッソ回帰の利点として,変数選択に利用しやすいという点が挙げられる.ラッソ回帰ではいくつかの変数に対する回帰係数を0と推定するため,変数を減らすようにモデルのパラメータを推定していくことになる.
ラッソ回帰は次のように実行することができる.
y <- BGSgirls$WT18
X <- subset(BGSgirls, select=-WT18) %>% as.matrix()
Lasso <- cv.glmnet(y=y,x=X, alpha=1)## 12 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) -1.145936e+02
## WT2 .
## HT2 .
## WT9 1.660622e-03
## HT9 .
## LG9 .
## ST9 4.801142e-04
## HT18 6.870476e-01
## LG18 9.228996e-02
## ST18 .
## BMI18 2.573431e+00
## Soma 2.491181e-01回帰係数が.と表示されているものが,0と推定されたものである.これによればこれらの変数はモデルから取り除いて良いことになる.
5.14 ElasticNet(エラスティックネット)
ElasticNetというモデルは,リッジ回帰とラッソ回帰を組み合わせたモデルである. 具体的には
\[\begin{align} \min_{\{\beta_j\}_{j=0}^{m}} \sum_{i=1}^n (y_i - \boldsymbol x^\top \boldsymbol \beta)^2 + \lambda \left( \alpha \sum_{j=1}^m \beta_j^2 + (1 - \alpha)\sum_{j=1}^{m} |\beta_j| \right) \tag{5.5} \end{align}\]
としてパラメータの推定を行う.ここで\(0 \leq \alpha \leq 1\)であり,これはラッソとリッジのどちらのペナルティを重視するかのパラメータになっている.\(\alpha = 1\)の時はリッジ回帰と同等であり,\(\alpha = 0\)の時はラッソ回帰と同等となる.\(\alpha, \lambda\)の値は分析者の主観で決定する必要がある.クロスバリデーション(次回講義で扱う)によってこのパラメータを決める方法もある.
## 3 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) -58.8480724
## x1 .
## x2 0.7122561alphaの値を変えながら平均予測誤差を比較するコードを紹介しよう.
alphas <- seq(0,1,0.01)
for(i in 1:length(alphas)){
alpha <- alphas[i]
if(i == 1){
fit_best <- cv.glmnet(y=y, x=X, alpha=alpha)
score_best <- min(fit_best$cvm)
alpha_best <- alpha
}else{
fit_new <- cv.glmnet(y=y, x=X, alpha=alpha)
score_new <- min(fit_new$cvm)
alpha_new <- alpha
if(score_new < score_best){
fit_best <- fit_new
score_best <- score_new
alpha_best <- alpha_new
}
}
}##
## Call: cv.glmnet(x = X, y = y, alpha = alpha)
##
## Measure: Mean-Squared Error
##
## Lambda Index Measure SE Nonzero
## min 0.007 76 56.86 22.77 1
## 1se 7.394 1 74.58 19.86 0## [1] 0.58ここでは,alphaの値を0から1まで0.01刻みで大きくしながら,平均予測誤差が最も小さいものをfit_bestとして保持するようにしている.
この実装によれば,最も良いalphaの値は0.43となった.