Bab 7 Rancangan Split Blok

Filosofi dasar rancangan split blok mirip dengan strip plot - ada petak utama dan anak petak. Anak petak tersebut mengandung suatu aspek dari percobaan yang ingin ditekankan (diketahui pengaruhnya dengan ketepatan lebih tinggi). Dalam split blok kasus ini yang ditekankan bukan satu faktor, melainkan interaksi antara faktor. Oleh karena itu, faktor menjadi petak utama.

Rancangan split blok hanya dapat diterapkan dalam RAKL, tidak di RAL. Unit percobaan harus dipisahkan menjadi blok, lalu petak utama diacak di lajur dan baris blok tersebut. Pengacakan semua faktor di lajur dan baris tidak mungkin terjadi di satu unit percobaan yang hanya mengandung satu perlakuan atau satu kombinasi faktor sehingga dibutuhkan blok agar pengacakan semua kombinasi tersebut dapat dilakukan.

7.1 Pengacakan

Langkah pengacakannya adalah sebagai berikut:

• Pilihlah kelompok unit percobaan secara acak
• Tempatkan taraf-taraf faktor A secara acak pada setiap kelompok mengikuti plot lajur
• Tempatkan taraf-taraf faktor B secara acak pada setiap kelompok mengikuti plot baris.

7.1.1 Pengacakan di agricolae

Sebelum langkah-langkah pengacakan di atas diikuti, akan didefinisikan faktor yang akan dicobakan dan tarafnya. Hendak dicobakan pupuk dengan taraf “Kontrol,” “PK,” “N,” “NP,” “NK,” dan “NPK” serta genotipe beras dengan taraf IR-64 dan S-969.

P<-c("Kontrol", "PK", "N", "NP", "NK","NPK")
G<-c("IR-64","S-969")

Pengacakan split blok di agricolae cukup sederhana. Nama lain dari split blok adalah strip-plot, dan ada fungsi design.strip(faktor1, faktor2, nblok) di package tersebut:

baganSplitB<-agricolae::design.strip(P,G,r=4,serie=1)

Perlihatkan bagan percobaan:

knitr::kable(head(baganSplitB$book, n=10),
             col.names= c("Petak", "Blok",
                          "Pupuk", "Genotipe"))

Petak	Blok	Pupuk	Genotipe
11	1	PK	S-969
12	1	PK	IR-64
13	1	NPK	S-969
14	1	NPK	IR-64
15	1	Kontrol	S-969
16	1	Kontrol	IR-64
17	1	N	S-969
18	1	N	IR-64
19	1	NP	S-969
20	1	NP	IR-64

7.1.2 Pengacakan di edibble

Dalam rancangan strip plot, ada empat unit percobaan. Pengaruh blok tentu diaplikasikan ke blok, lalu pengaruh faktor ditaruh di lajur dan baris, serta interaksi di tiap unit. Maka, di edibble buat empat unit. Blok, lalu kolom dan baris yang nested_in(blok), dan petak yang di dalam blok - nested_in(blok) dan crossed_by(baris, kolom) - tiap petak merupakan gabungan dari baris dan kolom. Cara mendefinisikan kasus ini adalah dengan menyatakan bahwa petak crossed_by() terlebih dahulu, lalu nested_in() - di tiap blok, petak merupakan gabungan baris dan kolom. Karena operasi dalam kurung dilaksanakan terlebih dahulu, bentuknya menjadi nested_in(blok, crossed_by()).

Lalu, pengacakan dilakukan ke baris dan kolom.

library(edibble)

desSBlok<-design(name="Padi") %>%
  set_units(blok=4,
            baris=nested_in(blok,2),
            kolom=nested_in(blok,6),
            petak=nested_in(blok,crossed_by(baris,kolom))) %>%
  set_trts(Genotipe=G,
           Pupuk=P) %>%
  allot_trts(Genotipe~baris,
             Pupuk~kolom) %>%
  assign_trts("random", seed=420) %>% serve_table

knitr::kable(head(desSBlok,n=10))

blok	baris	kolom	petak	Genotipe	Pupuk
blok1	baris1	kolom1	petak1	S-969	NPK
blok1	baris2	kolom1	petak2	IR-64	NPK
blok1	baris1	kolom2	petak3	S-969	Kontrol
blok1	baris2	kolom2	petak4	IR-64	Kontrol
blok1	baris1	kolom3	petak5	S-969	PK
blok1	baris2	kolom3	petak6	IR-64	PK
blok1	baris1	kolom4	petak7	S-969	NP
blok1	baris2	kolom4	petak8	IR-64	NP
blok1	baris1	kolom5	petak9	S-969	N
blok1	baris2	kolom5	petak10	IR-64	N

Plot rancangan tersebut:

deggust::autoplot(desSBlok)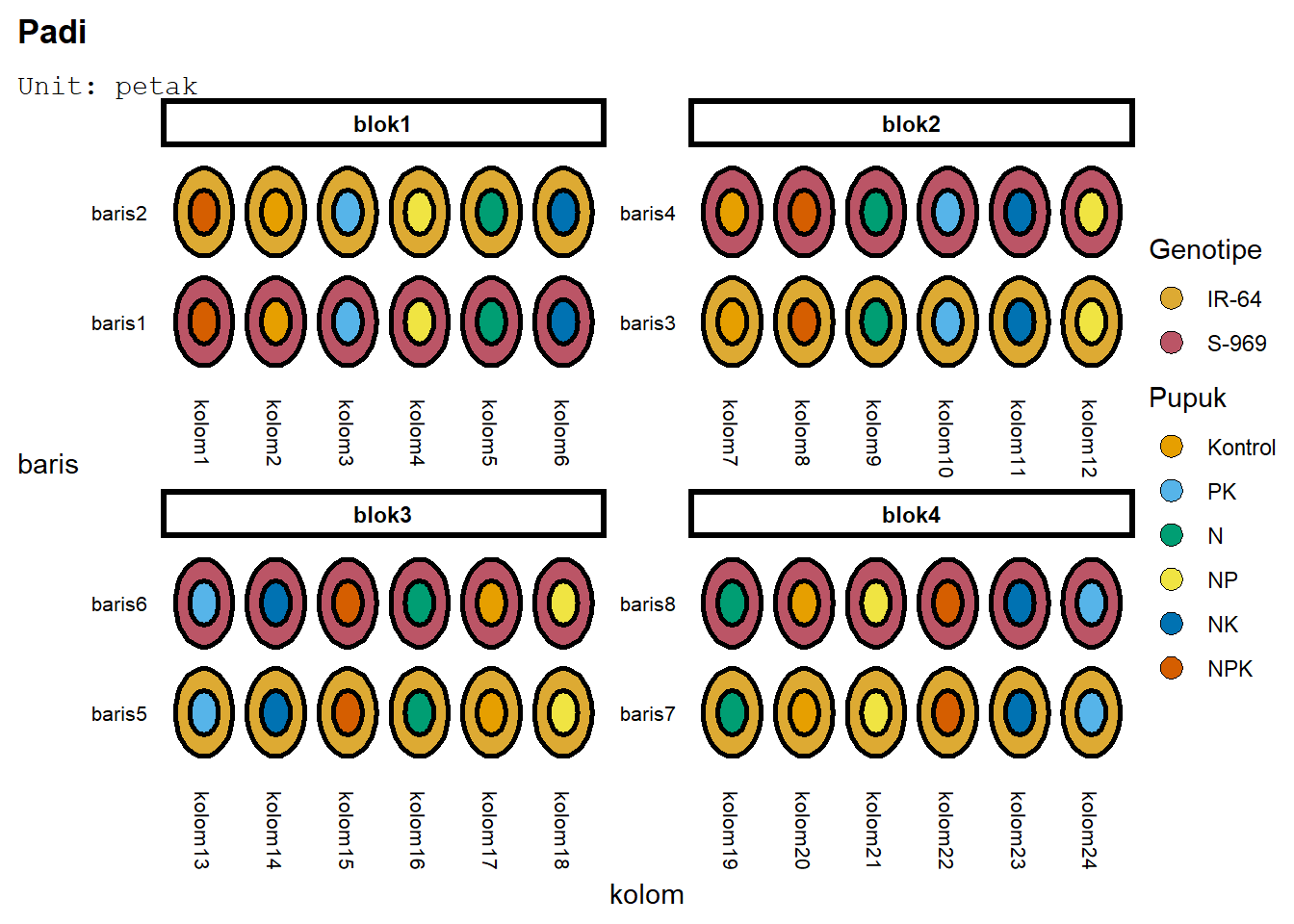

Bandingkan dengan default edibble:

strip <- takeout(menu_strip(t1 = 2, t2 = 6, r = 4, seed=420))
examine_recipe(strip)

## design("Strip-Plot Design | Strip-Unit Design") %>%
##   set_units(block = 4,
##             row = nested_in(block, 2),
##             col = nested_in(block, 6),
##             unit = nested_in(block, crossed_by(row, col))) %>%
##   set_trts(trt1 = 2,
##            trt2 = 6) %>%
##   allot_trts(trt1 ~ row,
##              trt2 ~ col) %>%
##   assign_trts("random", seed = 420) %>%
##   serve_table()

Plotnya akan relatif sama:

deggust::autoplot(strip)

7.2 ANOVA

7.2.1 Teori

Model linear aditif bagi split plot RAL adalah: \[ y_{ijk} = \mu + \alpha_i + K_{k}+ \delta_{ik} + \beta_j + \gamma_{jk}+(\alpha\beta)_{ij} + \epsilon_{ijk} \]

Dengan:

1. \(y_{ijk}\) adalah nilai pengamatan pada faktor A taraf ke-i dan faktor B taraf ke-j pada blok ke-k.
2. \(\mu\) komponen aditif dari rataan umum.
3. \(\alpha_i\) pengaruh utama faktor A. Diasumsikan \(\sum_{i=1}^a \alpha_i=0\) bagi model tetap dan \(\alpha\sim N(0,\sigma_a^2)\) bagi model acak.
4. \(\beta_{j}\) pengaruh utama faktor B. Diasumsikan \(\sum_{j=1}^b \beta_j=0\) bagi model tetap dan \(\beta\sim N(0,\sigma_b^2)\) bagi model acak.
5. \(K_{k}\) pengaruh utama kelompok.
6. \((\alpha\beta)_{ij}\) komponen interaksi faktor A dan faktor B. Diasumsikan \(\sum_{i=1}^p(\alpha\beta)_{ij}=\sum_{i=1}^t (\alpha\beta)_{ij}=0\) bagi model tetap dan \((\alpha\beta)_{ij}\sim N(0,\sigma_{ab}^2)\) bagi model acak.
7. \(\delta_{ik}\sim N(0,\sigma_{\delta}^2)\) komponen acak dari faktor A.
8. \(\gamma_{jk}\sim N(0,\sigma_{\ga,,a}^2)\) komponen acak dari faktor B.
9. \(\epsilon_{ijk}\sim N(0,\sigma^2)\) komponen acak interaksi dari faktor A dan B.

Dan hipotesis pengaruh petak utama, anak petak, dan interaksi. $$ \[\begin{aligned} \text{Pengaruh petak utama (Faktor A)}&:\\ H_{0}&:\alpha_{1}=\ldots=\alpha_{a}=0 \text{ faktor A tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu i di mana }\alpha_{i}\neq 0\\ \\ \text{Pengaruh anak petak (Faktor B)}&:\\ H_{0}&:\beta_{1}=\ldots=\beta_{b}=0 \text{ faktor B tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu j di mana }\beta_{j}\neq 0\\ \\ \text{Pengaruh interaksi }&:\\ H_{0}&:(\alpha\beta)_{11}=(\alpha\beta)_{12}=\ldots=(\alpha\beta)_{ab}=0 \text{ interaksi tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada sepasang ij di mana }(\alpha\beta)_{ij}\neq 0\\ \\ \text{Pengaruh kelompok}&:\\ H_{0}&:K_{1}=\ldots=K_{k}=0 \text{ Kelompok tidak berpengaruh pada respon}\\ H_{1}&: \text{Paling sedikit ada satu k di mana }K_{k}\neq 0\\ \end{aligned}\]

$$

Dan tabel ANOVA:

Sumber Keragaman	db	JK	KT	F-hit	F(dbP,dbG)
Blok	r-1	JKK	JKK/dbA	KTK/KTGA
A	a-1	JKA	JKA/dbA	KTA/KTGA
Galat (a)	(a-1)(r-1)	JKGA	JKGA/dbGA
B	(b-1)	JKB	JKB/dbB	KTB/KTGB
Galat (b)	(b-1)(r-1)	JKGA	JKGA/dbGB
AB	(a-1)(b-1)	JKAB	JKAB/dbAB	KTAB/KTGC
Galat (c)	(a-1)(b-1)(r-1)	JKGC	JKGC/dbGC
Total	abr-1	JKT

Untuk bagian pertama tabel, jumlah kuadrat dihitung dengan:

$$ \[\begin{aligned} FK&=\frac{y^2_{...}}{abr}\\ JKT&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(y_{ijk}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r y_{ijk}^2-FK\\ JKST_a&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(\bar{y}_{i.k}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{k=1}^r \frac{y_{i.k}^2}{b}-FK\\ JKA&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(\bar{y}_{i..}-\bar{y}_{...}\right)^2=\sum_{i=1}^a \frac{y_{i..}^2}{br}-FK\\ JKK&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r \left(\bar{y}_{..k}-\bar{y}_{...}\right)^2=\sum_{k=1}^r \frac{y_{..k}^2}{ab}-FK\\ JKG_{a}&=JKST_a-JKA-JKK\\ \end{aligned}\]

$$

Untuk bagian kedua tabel:

\[ \begin{aligned} JKB&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(\bar{y}_{.j.}-\bar{y}_{...}\right)^2=\sum_{j=1}^b \frac{y_{.j.}^2}{ar}-FK\\ JKST_{b}&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2=\sum_{k=1}^r\sum_{j=1}^b \frac{y_{.jk}^2}{a}-FK\\ JKG_{b}&=JKST_{b}-JKB\\ \end{aligned} \]

Dan untuk bagian terakhir tabel:

\[ \begin{aligned} JKP&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k-1}^r\left(\bar{y}_{ij}-\bar{y}_{..}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\frac{y_{ij.}^2}{r}-FK\\ JKAB&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k-1}^r\left(\bar{y}_{ij.}-\bar{y}_{i..}-\bar{y}_{.j.}+\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\sum_{k-1}^r\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2-JKA-JKB\\ &=JKP-JKB-JKA\\ JKG_{c}&=JKT-JKP-JKK-JKG_{a}-JKG_{b} \end{aligned} \]

7.2.2 Analisis dengan R

Load data:

library(googlesheets4)
library(data.table)

Data.SB<-as.data.table(read_sheet("https://docs.google.com/spreadsheets/d/1meWerIyAv1X8jtHXoFCTysvzPy91ptQL6F9sO_-RUNs/edit?usp=sharing"))

## √ Reading from "Data P10 STA1222".

## √ Range 'Sheet1'.

knitr::kable(Data.SB)

P	G	B1	B2	B3	B4
Kontrol	IR-64	20.7	32.1	29.5	37.7
Kontrol	S-969	27.7	33.0	26.3	37.7
PK	IR-64	30.0	30.7	25.5	36.9
PK	S-969	36.6	33.8	27.0	39.0
N	IR-64	39.9	41.5	46.4	44.5
N	S-969	37.4	41.2	45.4	44.6
NP	IR-64	40.8	43.5	43.3	43.4
NP	S-969	42.2	46.0	45.9	46.2
NK	IR-64	42.4	45.6	44.8	47.0
NK	S-969	39.8	39.5	40.9	44.0
NPK	IR-64	48.6	49.8	42.6	46.6
NPK	S-969	42.9	45.9	43.9	45.6

Karena data belum berbentuk long - satu baris adalah satu observasi, melt data tersebut. Tiap baris dalam data awal diidentifikasi oleh kombinasi pupuk dan genotipe, sehingga id.vars adalag c("P","G"):

Data.SB<-melt(
  Data.SB,
  id.vars=c("P","G"),
  value.name = "H"
)

knitr::kable(head(Data.SB,10))

P	G	variable	H
Kontrol	IR-64	B1	20.7
Kontrol	S-969	B1	27.7
PK	IR-64	B1	30.0
PK	S-969	B1	36.6
N	IR-64	B1	39.9
N	S-969	B1	37.4
NP	IR-64	B1	40.8
NP	S-969	B1	42.2
NK	IR-64	B1	42.4
NK	S-969	B1	39.8

Ubah kolom variable menjadi blok:

setnames(Data.SB,"variable", "B")

Untuk melakukan ANOVA, perlu ada struktur error yang khusus. Pada dasarnya, akan ada error khusus untuk faktor serta interaksinya, sehingga tulis Error(B:(P*G)) - akan dihitung Error(B:P), Error(B:G), dan Error(B:(G:P)), atau error tiap faktor dan interaksinya di tiap ulangan (blok). Spesifikasi lain adalah:

aov.SB<-aov(H~P*G+B+Error(B:(P*G)),Data.SB)

## Warning in aov(H ~ P * G + B + Error(B:(P * G)), Data.SB): Error() model is singular

summary(aov.SB)

## 
## Error: B:P
##           Df Sum Sq Mean Sq F value   Pr(>F)    
## P          5 1674.8   335.0  18.767 5.62e-06 ***
## B          3  197.1    65.7   3.681   0.0362 *  
## Residuals 15  267.7    17.8                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: B:G
##           Df Sum Sq Mean Sq F value Pr(>F)
## G          1  0.035  0.0352   0.032   0.87
## Residuals  3  3.329  1.1097               
## 
## Error: B:P:G
##           Df Sum Sq Mean Sq F value Pr(>F)  
## P:G        5  78.59   15.72   4.504 0.0105 *
## Residuals 15  52.35    3.49                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

aov.SB1<-aov(H~P*G+B+Error(B:P*B:G),Data.SB)

## Warning in aov(H ~ P * G + B + Error(B:P * B:G), Data.SB): Error() model is singular

summary(aov.SB1)

## 
## Error: B:P
##           Df Sum Sq Mean Sq F value   Pr(>F)    
## P          5 1674.8   335.0  18.767 5.62e-06 ***
## B          3  197.1    65.7   3.681   0.0362 *  
## Residuals 15  267.7    17.8                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: B:G
##           Df Sum Sq Mean Sq F value Pr(>F)
## G          1  0.035  0.0352   0.032   0.87
## Residuals  3  3.329  1.1097               
## 
## Error: B:P:G
##           Df Sum Sq Mean Sq F value Pr(>F)  
## P:G        5  78.59   15.72   4.504 0.0105 *
## Residuals 15  52.35    3.49                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Pastikan ada kurung, karena anova akan salah tanpa kurung:

aov.SB1<-aov(H~P*G+B+Error(B:P*G),Data.SB)

## Warning in aov(H ~ P * G + B + Error(B:P * G), Data.SB): Error() model is singular

summary(aov.SB1)

## 
## Error: G
##   Df  Sum Sq Mean Sq
## G  1 0.03521 0.03521
## 
## Error: B:P
##           Df Sum Sq Mean Sq F value   Pr(>F)    
## P          5 1674.8   335.0  18.767 5.62e-06 ***
## B          3  197.1    65.7   3.681   0.0362 *  
## Residuals 15  267.7    17.8                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: B:P:G
##           Df Sum Sq Mean Sq F value  Pr(>F)   
## P:G        5  78.59  15.718   5.081 0.00444 **
## Residuals 18  55.68   3.093                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Atau, dapat digunakan fungsi strip.plot(blok, faktor 1, faktor 2, respon) dari agricolae:

library(agricolae)

out1<-with(Data.SB,strip.plot(B,P,G,H))

## 
## ANALYSIS STRIP PLOT:  H 
## Class level information
## 
## P    :  Kontrol PK N NP NK NPK 
## G    :  IR-64 S-969 
## B    :  B1 B2 B3 B4 
## 
## Number of observations:  48 
## 
## model Y: H ~ B + P + Ea + G + Eb + G:P + Ec 
## 
## Analysis of Variance Table
## 
## Response: H
##     Df  Sum Sq Mean Sq F value    Pr(>F)    
## B    3  197.11   65.70                      
## P    5 1674.80  334.96 18.7668 5.616e-06 ***
## Ea  15  267.73   17.85                      
## G    1    0.04    0.04  0.0317   0.86997    
## Eb   3    3.33    1.11                      
## G:P  5   78.59   15.72  4.5038   0.01047 *  
## Ec  15   52.35    3.49                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## cv(a) = 10.6 %, cv(b) = 2.7 %, cv(c) = 4.7 %, Mean = 39.71458

Uji lanjut untuk tiap faktor dapat mudah dilakukan. gl.a adalah derajat bebas galat a, dan Ea galat A.

test1<-agricolae::LSD.test(Data.SB$H, Data.SB$P, out1$gl.a, out1$Ea)
test1$statistics

##    MSerror Df     Mean       CV t.value      LSD
##   17.84854 15 39.71458 10.63779 2.13145 4.502424

plot(test1)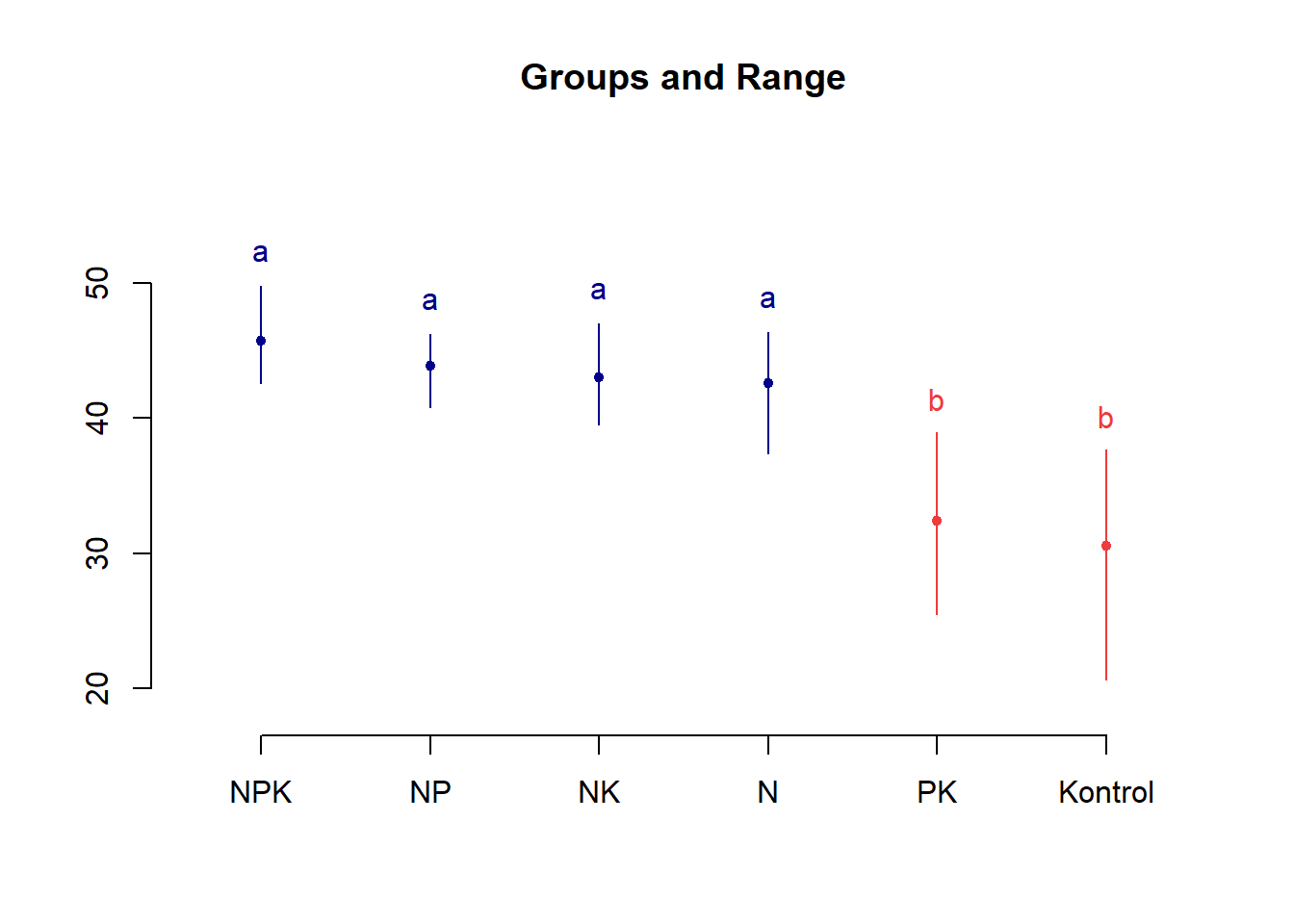

Namun, tampaknya tidak dilakukan penyesuaian pada KTG sehingga perlu dilakukan perhitungan manual jika ingin ada penyesuaian tersebut:

7.2.3 Latihan: Huasahuasi

Sedang diteliti ambang batas curah hujan sebagai dukungan untuk aplikasi fungisida waktu dalam pengendalian penyakit busuk daun kentang di Peru menggunakan strip plot.

library(agricolae)

data(huasahuasi)
str(huasahuasi)

## List of 2
##  $ AUDPC:'data.frame':   450 obs. of  13 variables:
##   ..$ block: Factor w/ 3 levels "I","II","III": 1 1 1 1 1 1 1 1 1 1 ...
##   ..$ trt  : Factor w/ 3 levels "40mm","7-days",..: 1 1 1 1 1 1 1 1 1 1 ...
##   ..$ clon : Factor w/ 5 levels "C386209.10","C387164.4",..: 2 2 2 2 2 2 2 2 2 2 ...
##   ..$ plant: num [1:450] 1 2 3 4 5 6 7 8 9 10 ...
##   ..$ d44  : num [1:450] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ d51  : num [1:450] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ d58  : num [1:450] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ d65  : num [1:450] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ d72  : num [1:450] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ d79  : num [1:450] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ d86  : num [1:450] 0 0 0 0 0 0 0 0 0 0 ...
##   ..$ d93  : num [1:450] 0 0 0 1 1 0 0 0 0 0 ...
##   ..$ d100 : num [1:450] 0 0 0 1 1 0 0 0 0 0 ...
##  $ YIELD:'data.frame':   45 obs. of  6 variables:
##   ..$ block: Factor w/ 3 levels "I","II","III": 1 1 1 1 1 1 1 1 1 1 ...
##   ..$ trt  : Factor w/ 3 levels "40mm","7-days",..: 1 1 1 1 1 2 2 2 2 2 ...
##   ..$ clon : Factor w/ 5 levels "C386209.10","C387164.4",..: 2 1 3 5 4 2 1 3 5 4 ...
##   ..$ y1da : num [1:45] 22.8 10.8 1.6 10.9 3.5 ...
##   ..$ y2da : num [1:45] 5.5 8 11.7 9.9 5.1 7 12.5 9.15 8.8 4.6 ...
##   ..$ y3da : num [1:45] 4.14 6.1 4.15 5.2 2.4 7.6 3.6 4.9 5.9 3.5 ...

Karena ada dua data.frame, ambil data.frame YIELD:

YIELD<-huasahuasi$YIELD
str(YIELD)

## 'data.frame':    45 obs. of  6 variables:
##  $ block: Factor w/ 3 levels "I","II","III": 1 1 1 1 1 1 1 1 1 1 ...
##  $ trt  : Factor w/ 3 levels "40mm","7-days",..: 1 1 1 1 1 2 2 2 2 2 ...
##  $ clon : Factor w/ 5 levels "C386209.10","C387164.4",..: 2 1 3 5 4 2 1 3 5 4 ...
##  $ y1da : num  22.8 10.8 1.6 10.9 3.5 ...
##  $ y2da : num  5.5 8 11.7 9.9 5.1 7 12.5 9.15 8.8 4.6 ...
##  $ y3da : num  4.14 6.1 4.15 5.2 2.4 7.6 3.6 4.9 5.9 3.5 ...

Ada y1da, y2da, dan y3da. Respon yield merupakan penjumlahan dari ketiga respon tersebut - YIELD$yield<- y1da+y2da+y3da, dan perlakuan ada di trt dan clon.

Buat bagan percobaan dengan edibble dan lakukan ANOVA!