Bab 3 Perbandingan Nilai Tengah Perlakuan

ANOVA pada RAK, RAKL, dan RBSL hanya dapat menguji ketidaknolan efek perlakuan. Semisal diketahui setidaknya salah satu perlakuan tersebut memiliki efek, lalu bagaimana? Tentu ada pertanyaan-pertanyaan lain yang menarik, misal:

Perlakuan mana yang memberi efek terbesar atau terkecil?
Perlakuan mana yang memberi efek mirip?
Apakah perlakuan dapat dikelompokkan?

Dan pertanyaaan-pertanyaan lain. Pertanyaan itu dijawab uji lanjut.

3.1 LSD/BNT

Uji BNT menguji perlakuan secara berpasangan. Menurut Carmer dan Swanson (1973) di Montgomery (2017), BNT efektif mendeteksi perbedaan rataan perlakuan jika diaplikasikan **setelah* uji-F di ANOVA signifikan di taraf 5 persen. Hipotesis perbandingan BNT sebagai berikut: \[ \begin{aligned} H_{0}&: \mu_{i}=\mu_{j}\\ H_{1}&:\mu_{i}\neq \mu_{j} \end{aligned} \] Dengan nilai kritis BNT sebagai berikut: \[ \begin{aligned} LSD&=t_{\alpha/2,db_{g}}S_{\bar{y}_{i.}-\bar{y}_{j.}}\\ S_{\bar{y}_{i.}-\bar{y}_{j.}}&=\sqrt{KTG\left(\frac{1}{r_{i}}+\frac{1}{r_{j}}\right)} \end{aligned} \] Jika ulangan sama, \(S_{\bar{y}_{i.}-\bar{y}_{j.}}=\sqrt{\frac{2KTG}{r}}\) (kenapa?). Prosedur uji tersebut adalah membandingkan \(\bar{y}_{i.}-\bar{y}_{j.}\) dengan nilai kritis. Implementasi di R (dari data RAL sebelumnya) sebagai berikut:

library(googlesheets4)
#baca sheet
DataRAL<-read_sheet("https://docs.google.com/spreadsheets/d/1Bzm_R2Zd4Zbij7BO7LGDJW83DU6T3Wh7R38NN5DHCBs/edit?usp=sharing")

## √ Reading from "DataRAL".

## √ Range 'Sheet1'.

#reshaping
library(reshape2)

RALMelt<- melt(DataRAL,
               #variabel yang membedakan tiap baris di tabulasi asli:
               id.vars=c("Dosis"),
               
               #kolom yang ingin digabung jadi 1
               measured.vars=as.character(seq(1,8)),
               value.name="Perkecambahan")
colnames(RALMelt)[2]<-"Ulangan"
RALMelt$Dosis<-as.factor(RALMelt$Dosis)

#anova
aov_RAL <- aov(Perkecambahan ~ Dosis, data = RALMelt)
summary(aov_RAL)

##             Df Sum Sq Mean Sq F value  Pr(>F)    
## Dosis        4 2556.4   639.1   51.36 3.6e-14 ***
## Residuals   35  435.5    12.4                    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Gunakan library agricolae:

library(agricolae)
LSD<-agricolae::LSD.test(aov_RAL, "Dosis") #hasil anova, perlakuan


knitr::kables(
  list(
    knitr::kable(LSD$statistics[6]), #tabel 1
    knitr::kable(LSD$groups, col.names = c("Rata-Rata per Taraf",
                                           "Kelompok")) #tabel 2
  ),
)

	LSD
	3.580545

	Rata-Rata per Taraf	Kelompok
0	100.00	a
16	100.00	a
32	90.25	b
64	85.00	c
48	80.00	d

Atau susun argumen sebagai berikut,

library(agricolae)
LSD2<-agricolae::LSD.test(RALMelt$Perkecambahan, RALMelt$Dosis,35,12.4) #respon, perlakuan, dbg, KTG

knitr::kables(
  list(
    knitr::kable(LSD2$statistics[6]) , #tabel 1
    knitr::kable(LSD2$groups, col.names =c("Rata-Rata per Taraf",
                                           "Kelompok")) #tabel 2
    ),
)

	LSD
	3.574374

	Rata-Rata per Taraf	Kelompok
0	100.00	a
16	100.00	a
32	90.25	b
64	85.00	c
48	80.00	d

Dapat dicek sendiri bahwa pengelompokan tersebut benar. Dapat juga dibuat visualisasi:

plot(LSD,horiz=T)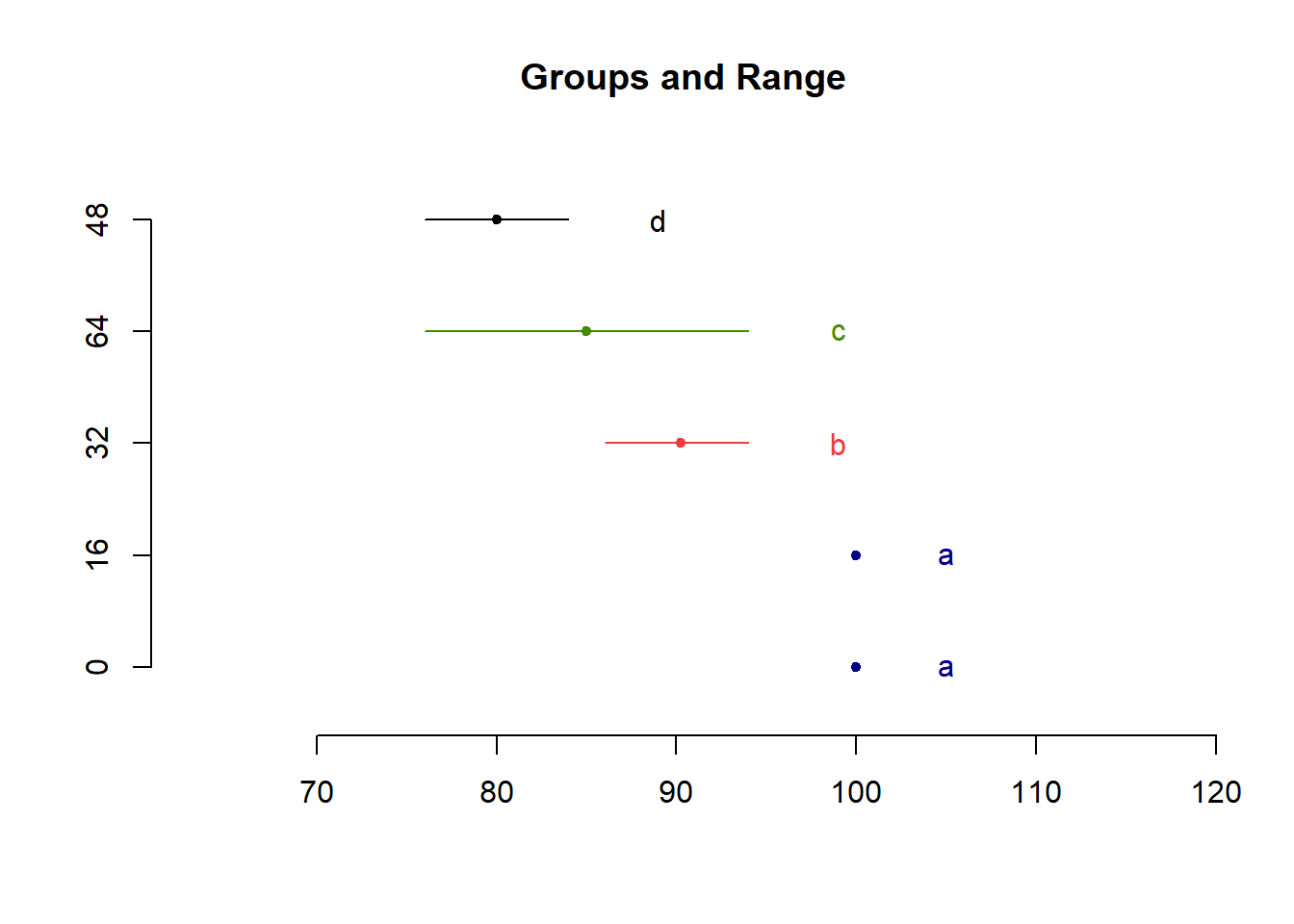

Note, BNT menguji semua perlakuan secara berpasangan, sehingga tidak bisa memilih perbandingan tertentu saja (misal, rata-rata terbesar vs terkecil). Selain itu, BNT memiliki kelemahan, yaitu hanya dapat mengontrol tingkat kesalahan uji sepasang rata-rata saja. Jika ada beberapa pasang rata-rata, tingkat kesalahan berpotensial lebih besar. Banyak perbandingan \(g=k(k-1)/2\) (dari permutasi), sehingga family error rate sebesar \(1-(1-\alpha)^g\). Perhitungan tersebut hanya merupakan kebalikan dari perhitungan \(P(\text{Tolak }H_{0}|H_{0} \text{ benar})\). \((1-\alpha)\). Jika diasumsikan perbandingan saling bebas, maka probabilitas tersebut menjadi \((1-\alpha)^g\).

3.2 BNJ

Lalu, bagaimana cari membuat uji yang mengontrol family error rate? BNJ mengontrol kesalahan di t buah perlakuan sebesar \(\alpha\), sehingga di tiap pasangan akan menarima kesalahan sebesar \(\alpha/2g\) karena uji dua arah menggunakan \(\alpha/2\) dan ada g ulangan. Jika jumlah perlakuan banyak, metode ini akan sangat ekstrim. Oleh karena itu, walaupun metode ini tidak terlalu sensitif, metode ini memisahkan perlakuan yang benar-benar beda. BNJ memiliki nilai kritis: \[ \begin{aligned} BNJ&=q_{\alpha;t;db_{g}}S_{\bar{y}}\\ S_{\bar{y}}&=\sqrt{KTG/r} \end{aligned} \] Dengan t jumlah perlakuan, q memiliki asal statistik studentized range. Jika ulangan tak sama, r didekati: \[ r_{h}=\frac{t}{\sum_{i=1}^t 1/r_{i}} \] Dengan langkah-langkah uji:

Urutkan rataan perlakuan dari yang terkecil sampai yang terbesar atau sebaliknya
Nilai awal i=1 (dari kiri) dan j =1 (dari kanan)
Hitung beda antara rataan perlakuan terkecil ke-i dengan terbesar ke-j kemudian bandingkan dengan nilai BNJ, jika beda rataan perlakuan lebih kecil lanjutkan ke langkah 5 (taktolak \(H_{0}\)) dan jika tidak lanjutkan ke langkah 4
Berikan j = j+1, jika j<p kembali ke langkah 3
Buatlah garis mulai rataan perlakuan ke-i sampai ke perlakuan ke-j
Berikan I = i+1, jika i<p kembali ke langkah 3
Stop

Implementasi uji tersebut di R adalah:

tukey <- TukeyHSD(aov_RAL, 'Dosis', conf.level = 0.95)


library(kableExtra)
knitr::kable(tukey$Dosis, col.names = c(" ",
                                        " Bawah",
                                        " Atas",
                                        " ")) %>%
add_header_above(c(" Taraf"=1, "Beda"=1, "Batas Selang Kepercayaan"=2, "P-Value"=1))

Taraf	Beda	Batas Selang Kepercayaan		P-Value
		Bawah	Atas
16-0	0.00	-5.0708064	5.0708064	1.0000000
32-0	-9.75	-14.8208064	-4.6791936	0.0000306
48-0	-20.00	-25.0708064	-14.9291936	0.0000000
64-0	-15.00	-20.0708064	-9.9291936	0.0000000
32-16	-9.75	-14.8208064	-4.6791936	0.0000306
48-16	-20.00	-25.0708064	-14.9291936	0.0000000
64-16	-15.00	-20.0708064	-9.9291936	0.0000000
48-32	-10.25	-15.3208064	-5.1791936	0.0000130
64-32	-5.25	-10.3208064	-0.1791936	0.0393966
64-48	5.00	-0.0708064	10.0708064	0.0548433

Cara membaca tabel tersebut adalah melihat apakah selang kepercayaan (lwr dan upper) memiliki tanda positif dan negatif. Jika ada dua tanda, berarti nol termasuk di selang kepercayaan, sehingga kita belum dapat menyatakan rataan perlakuan tersebut beda. Proses tersebut dapat divisualisikan:

plot(tukey, las = 1, col = 'dark blue')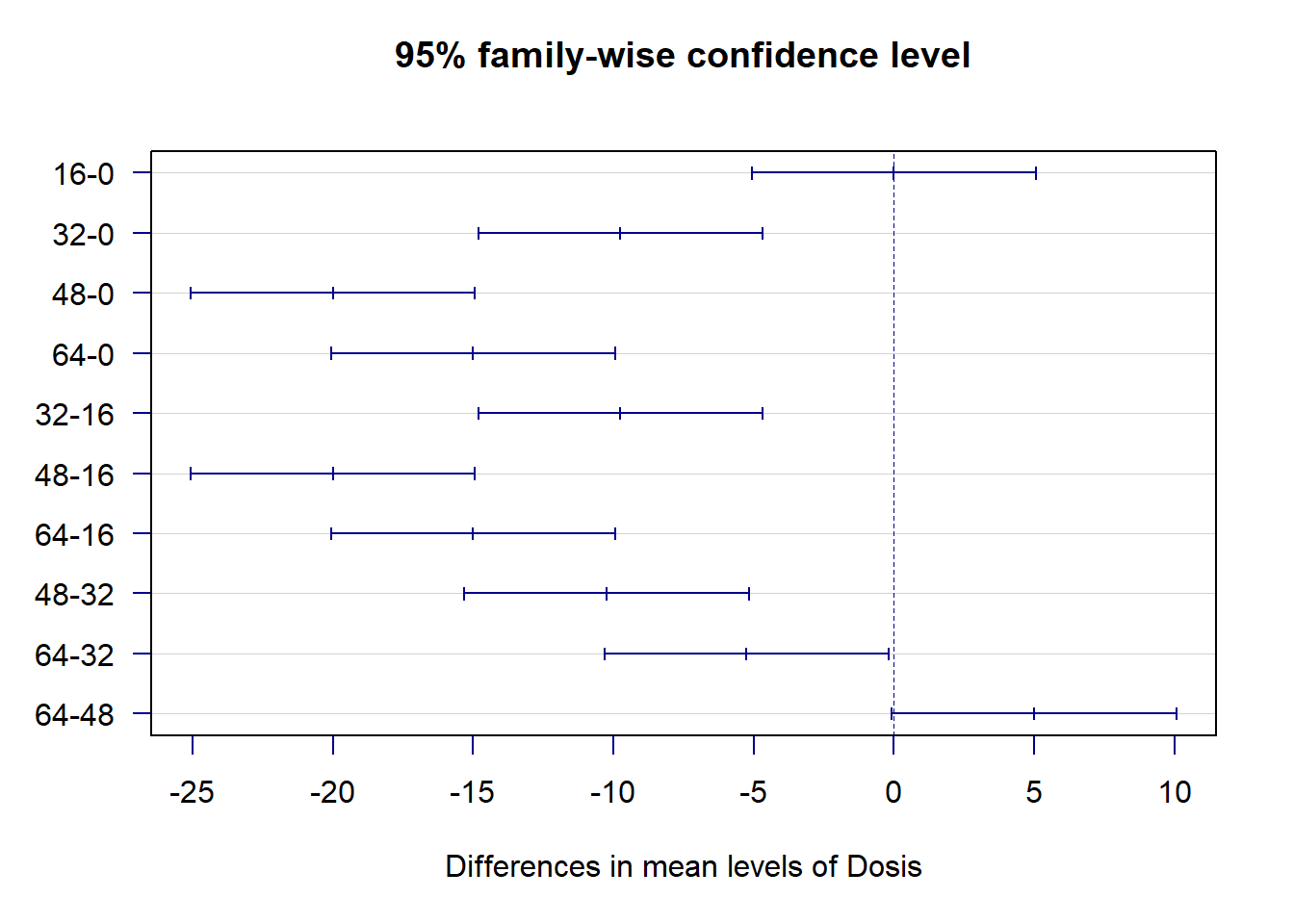

Analisis di python dapat dimulai dengan melakukan reshape kepada data. Detail dari proses ini sudah dijelaskan sebelumnya:

import pandas as pd

RALData = pd.read_csv("https://docs.google.com/spreadsheets/d/e/2PACX-1vT8sPRuEulqieCMFJK4sKReRjtuXOQD_xwTlI3RB619yYwSWwb776-Dmu5UY5P44hy5MsMPJPsjcZUp/pub?gid=0&single=true&output=csv")
RALMeltpy=pd.melt(RALData, id_vars=['Dosis'], value_vars=[str(x) for x in range(1,9)])
RALMeltpy.rename(columns = {'variable':'Ulangan', 'value':'Produksi'}, inplace = True)
RALMeltpy.head()

##    Dosis Ulangan  Produksi
## 0      0       1       100
## 1     16       1       100
## 2     32       1        90
## 3     48       1        80
## 4     64       1        90

Lalu, statsmodels memiliki fungsi MultiComparison(respon, perlakuan):

import statsmodels.formula.api as smf
import statsmodels.stats.multicomp as multi 

mcDosis = multi.MultiComparison(RALMeltpy['Produksi'],RALMeltpy['Dosis'])
Results = mcDosis.tukeyhsd()
print(Results)

##  Multiple Comparison of Means - Tukey HSD, FWER=0.05  
## ======================================================
## group1 group2 meandiff p-adj   lower    upper   reject
## ------------------------------------------------------
##      0     16      0.0    0.9  -5.0708   5.0708  False
##      0     32    -9.75  0.001 -14.8208  -4.6792   True
##      0     48    -20.0  0.001 -25.0708 -14.9292   True
##      0     64    -15.0  0.001 -20.0708  -9.9292   True
##     16     32    -9.75  0.001 -14.8208  -4.6792   True
##     16     48    -20.0  0.001 -25.0708 -14.9292   True
##     16     64    -15.0  0.001 -20.0708  -9.9292   True
##     32     48   -10.25  0.001 -15.3208  -5.1792   True
##     32     64    -5.25 0.0394 -10.3208  -0.1792   True
##     48     64      5.0 0.0549  -0.0708  10.0708  False
## ------------------------------------------------------

Hasil sama seperti R. Hasil juga dapat di-plot dengan:

import matplotlib.pyplot as plt

tukPlot=Results.plot_simultaneous()
plt.show()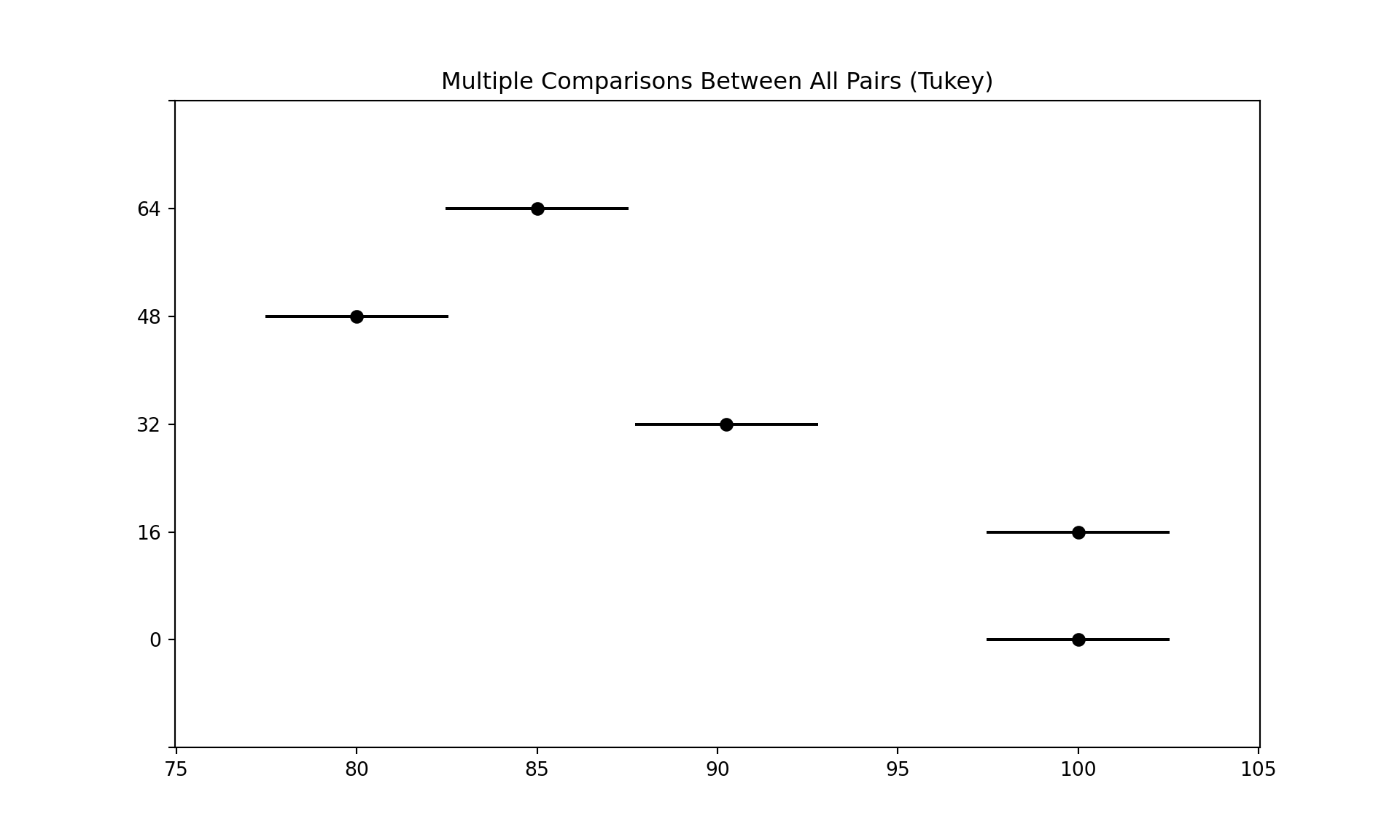

Tingkat kepercayaan juga dapat diubah:

Results = mcDosis.tukeyhsd(alpha=0.01)
print(Results)

##  Multiple Comparison of Means - Tukey HSD, FWER=0.01  
## ======================================================
## group1 group2 meandiff p-adj   lower    upper   reject
## ------------------------------------------------------
##      0     16      0.0    0.9  -6.2115   6.2115  False
##      0     32    -9.75  0.001 -15.9615  -3.5385   True
##      0     48    -20.0  0.001 -26.2115 -13.7885   True
##      0     64    -15.0  0.001 -21.2115  -8.7885   True
##     16     32    -9.75  0.001 -15.9615  -3.5385   True
##     16     48    -20.0  0.001 -26.2115 -13.7885   True
##     16     64    -15.0  0.001 -21.2115  -8.7885   True
##     32     48   -10.25  0.001 -16.4615  -4.0385   True
##     32     64    -5.25 0.0394 -11.4615   0.9615  False
##     48     64      5.0 0.0549  -1.2115  11.2115  False
## ------------------------------------------------------

3.3 Uji Duncan

Uji Duncan intinya mirip dengan uji Tukey, tetapi nilai pembanding di uji Duncan meningkat tergantung jarak dari perlakuan yang dibandingkan. Uji tersebut memiliki nilai kritis: \[ \begin{aligned} R_{p}&=r_{\alpha;t;db_{g}}S_{\bar{y}}\\ S_{\bar{y}}&=\sqrt{KTG/r} \end{aligned} \] Dan jika jumlah ulangan tak sama dapat didekati rataan harmonik juga. t adalah beda urutan perlakuan kedua kelompok. Misal membandingkan perlakuan terbesar (1) dan terkecil (4) dari 4 perlakuan akan menghasilkan t=3. Langkah uji mirip dengan Tukey, yaitu:

Urutkan rataan perlakuan dari yang terkecil sampai yang terbesar atau sebaliknya
Nilai awal i=1 (dari kiri) dan j =1 (dari kanan)
Hitung beda antara rataan perlakuan terkecil ke-i dengan terbesar ke-j kemudian bandingkan dengan nilai BNJ, jika beda rataan perlakuan lebih kecil lanjutkan ke langkah 5 (taktolak \(H_{0}\)) dan jika tidak lanjutkan ke langkah 4
Berikan j = j+1, jika j<p kembali ke langkah 3
Buatlah garis mulai rataan perlakuan ke-i sampai ke perlakuan ke-j
Berikan I = i+1, jika i<p kembali ke langkah 3
Stop

Langsung uji:

duncan <- duncan.test(aov_RAL, 'Dosis', alpha = 0.05) #Bisa Model aov atau lm
knitr::kable(duncan$duncan)

	Table	CriticalRange
2	2.871006	3.580545
3	3.018061	3.763944
4	3.113890	3.883455
5	3.182680	3.969247

knitr::kable(duncan$groups)

	Perkecambahan	groups
0	100.00	a
16	100.00	a
32	90.25	b
64	85.00	c
48	80.00	d

Dan dapat divisualisasikan:

plot(duncan, horiz = TRUE, las = 1)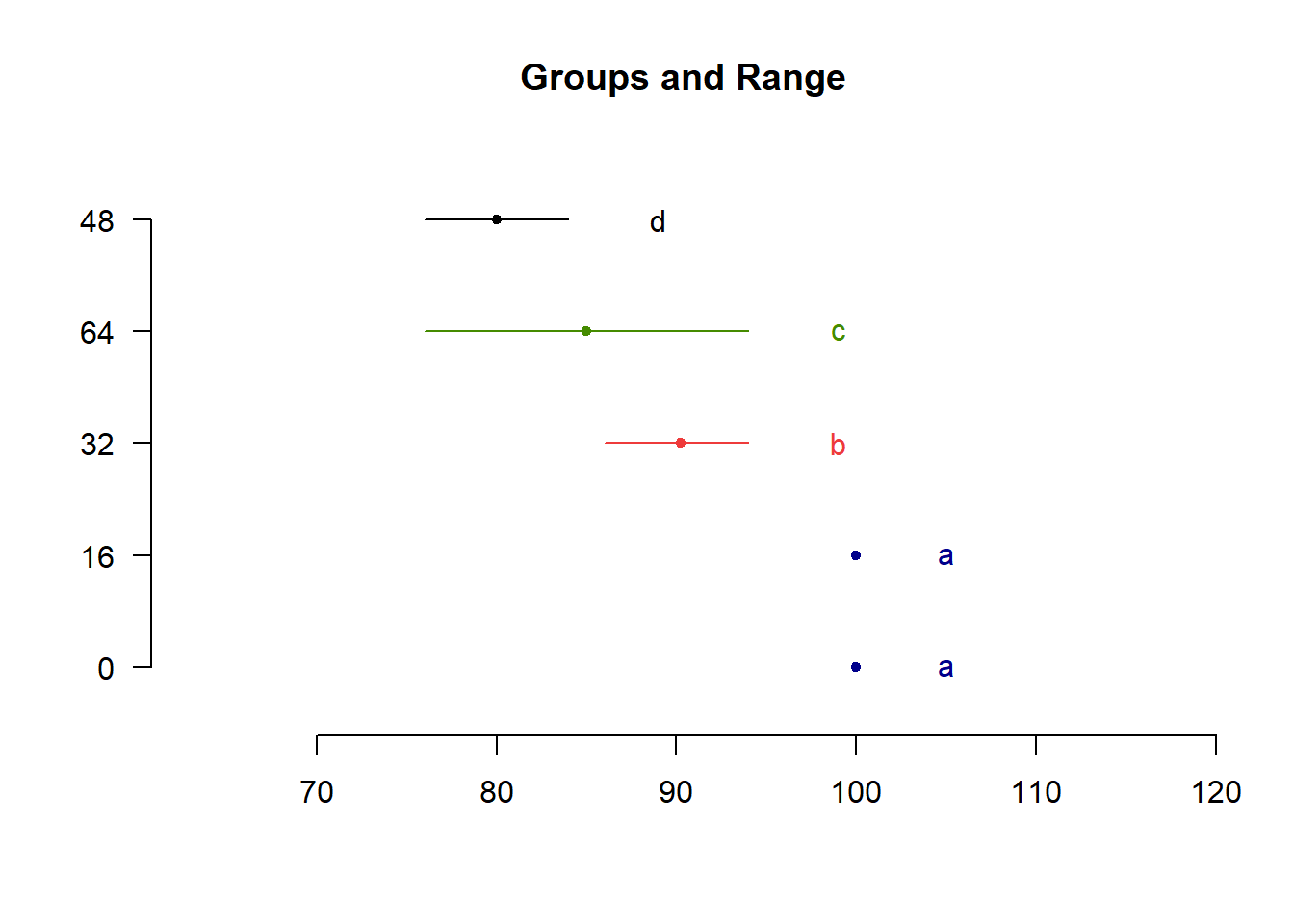

Note bahwa Uji Tukey menyatakan dosis 64 tak beda dengan dosis 48, padahal uji Duncan dan LSD menyatakan dosis tersebut beda. Hal tersebut menunjukkan kurang sensitifnya uji Tukey.

3.4 Kontras

Kontras merupakan kombinasi linear dari rataan perlakuan. Sebuah kombinasi linear tersusun atas seperangkat objek. Setiap objek dikalikan dengan suatu konstanta, dan hasil perkalian semua objek dan konstanta ditambahkan. Pada intinya, setiap rataan perlakuan akan dikalikan dengan suatu konstanta dan hasil perkalian tersebut akan ditambahkan. Bentuk umum kontras adalah: \[ \begin{aligned} H_{0}&: c_{1}\mu_{1}+c_{2}\mu_{2}+\cdots+c_{t}\mu_{t}=\sum_{i=1}^t c_{i}\mu_{i}=0\\ H_{1}&: c_{1}\mu_{1}+c_{2}\mu_{2}+\cdots+c_{t}\mu_{t}=\sum_{i=1}^t c_{i}\mu_{i}\neq 0 \end{aligned} \] Yang diduga dengan \[ C=\sum_{i=1}^t c_{i}y_{i.} \] Dengan \(y_{i.}\) adalah total di perlakuan ke-i. Kontras memiliki syarat: \[ \sum_{i=1}^t c_{i}=0 \] Selain itu, kontras disebut ortogonal jika hasil suatu uji tidak memengaruhi hasil uji lain. Sebagai contoh, kontras: \[ \begin{aligned} H^{(1)}_0\colon \mu_1 = \mu_2\\ H^{(2)}_0\colon \mu_1 = \mu_3\\ H^{(3)}_0\colon \mu_2 = \mu_3\\ \end{aligned} \] Tidak ortogonal. Bayangkan bahwa kita menolak \(H_{0}^3\), tetapi tak tolak hipotesis lainnya. Ini merupakan kontradiksi karena \(\mu_{1}=\mu_{2}\) dan \(\mu_{1}=\mu_{3}\) secara logis memberi implikasi \(\mu_{2}=\mu_{3}\). Namun, uji mengatakan sebaliknya.

Untuk melihat kenapa hal tersebut terjadi, kontras dapat dilihat lebih lanjut: \[ \begin{aligned} H^{(1)}_0\colon 1\mu_1-1\mu_{2}+0\mu_{3} = 0\\ H^{(2)}_0\colon 1\mu_1+0\mu_2-1\mu_3=0\\ H^{(3)}_0\colon 0\mu_1+1\mu_2-1\mu_3=0\\ \end{aligned} \] Dapat dengan mudah diverifikasi bahwa semua \(\sum_{i=1}^t c_{i}\) adalah nol. Namun, jika kita kalikan kontras pertama (\(c_{i}\)) dan kontras kedua (\(d_{i}\)) serta melihat hasilnya, maka kita akan temukan \(\sum_{i=1}^t c_{i}d_{i}=1+0+0=1\neq 0\). Bandingkan dengan contoh ini:

Sebuah percobaan menguji efek pemberian nitrogen pada pertumbuhan rumput. Perlakuan dalam percobaan tersebut ada empat, yaitu tidak diberi nitrogen sebagai kontrol (1), diberi nitrogen di musim gugur (2), diberi nitrogen di musim semi (3), dan diberikan pada kedua musim (4). Ingin diketahui:

Apakah terdapat perbedaan pertumbuhan rumput dari yang tidak diberi nitrogen dengan diberi nitrogen?

Apakah ada perbedaan pertumbuhan rumput jika diberikan nitrogen pada saat musim gugur dengan musim semi?

Apakah ada perbedaan pertumbuhan rumput jika diberikan pada saat musim gugur atau musim semi dengan diberikan pada kedua musim tersebut?

Kontras tersebut dapat disusun: \[ \begin{aligned} H^{(1)}_0\colon 3\mu_1-1\mu_{2}-1\mu_{3}-1\mu_{4} = 0\\ H^{(2)}_0\colon 0\mu_1+1\mu_{2}-1\mu_{3}-0\mu_{4}=0\\ H^{(3)}_0\colon 0\mu_1+1\mu_2+1\mu_3-2\mu_{4}=0\\ \end{aligned} \] Alasan penyusunan kontras sebagai berikut dapat ditelusuri dari beberapa prinsip:

Di sebuah kontras, perlakuan yang tidak ingin dibandingkan mendapatkan \(c_{i}=2\). Misal, di kontras kedua hanya dibandingkan musim gugur (\(\mu_{2}\)) dan musim semi (\(\mu_{3}\)), sehingga koefisien di tanpa nitrogen dan kedua musim (\(\mu_{1},\mu_{4}\)) nol. Begitu juga di kontras ketiga, perlakuan tanpa nitrogen tidak ingin dibandingkan sehingga koefisiennya nol.
Pastikan bobot tiap perlakuan sama. Suatu kontras pada dasarnya membagi perlakuan menjadi dua kelompok yang hendak dibandingkan. Namun, agar perbandingan tersebut adil, bobot perlakuan harus sama. Misal, di hipotesis pertama, hanya ada 1 perlakuan tanpa nitrogen sedangkan ada 3 perlakuan dengan nitrogen. Jika kita membandingkan rata-rata 1 perlakuan tanpa nitrogen dengan hasil tambah tiga perlakuan dengan nitrogen, pasti tidak adil. Anggap saja \(\mu_{1}=\mu_{2}=\mu_{3}=\mu_{4}\), seharusnya kontras menunjukkan sisi kiri sama dengan sisi kanan. Namun, jika kita melakukan pertambahan secara naif, akan muncul perbandingan \(\mu_{1}\neq3\mu_{1}\). Oleh karena itu \(\mu_{1}\) harus kita boboti 3 agar perbandingannya adil. Dalam kasus \(H_{0}\) benar tadi, pembobotan \(\mu_{1}\) dengan 3 menghasilkan \(3\mu_{1}=3\mu_{1}\).
Pastikan tanda antara kelompok berbeda. Satu kelompok akan memiliki tanda positif dan satu kelompok memiliki tanda negatif. Ini dikarenakan jumlah koefisien nol sehingga perlu tanda positif dan negatif untuk menghasilkan angka tersebut.

Sekarang, dapat dipikirkan secara logis implikasi dari tiap uji: \[ \begin{aligned} H^{(1)}_0&\colon \mu_1=\frac{\mu_{2}+\mu_{3}+\mu_{4}}{3}\\ H^{(2)}_0&\colon \mu_{2}=\mu_{3}\\ H^{(3)}_0&\colon \frac{\mu_2+\mu_3}{2}=\mu_{4}\\ \end{aligned} \] Tidak ada hipotesis yang saling berkontradiksi. Jika \(\mu_{2}\) tidak sama dengan \(\mu_{3}\), misal, hipotesis pertama dan ketiga masih dapat benar ataupun salah. Jika dijabarkan dalam perkataan, pengujian mengenai efek dari pemberian nitrogen dibandingkan dengan tidak sama sekali tidak memberi informasi mengenai efek pemberian nitrogen di dua musim dibandingkan dengan satu musim. Begitu juga, kedua uji tersebut tidak memberi informasi mengenai efek perbandingan nitrogen di musim semi atau gugur.

Secara formal, dapat kita lihat bahwa \(\sum_{i=1}^t c_{i}d_{i}=0\) untuk tiap kombinasi kontras. Dari aljabar linear, jika c dan d merupakan vektor, ini sama dengan hasil kali transpose c dengan d. Maka, buktikan di R:

kontras1<-c(3,-1,-1,-1)
kontras2<-c(0,1,-1,0)
kontras3<-c(0,1,1,-2)

#kali vektor
t(kontras1)%*%kontras2

##      [,1]
## [1,]    0

t(kontras1)%*%kontras3

##      [,1]
## [1,]    0

t(kontras2)%*%kontras3

##      [,1]
## [1,]    0

Oleh karena itu, kontras akan orthogonal jika \(\sum_{i=1}^t c_{i}d_{i}=0\). Keortogonalan berarti hasil satu uji bebas dari uji lain, sehingga jumlah kuadrat perlakuan dapat dipartisi.

3.4.1 Menyusun kontras ortogonal

Misalkan ada contoh:

Ingin dibandingkan 5 populasi dari data. Sebelumnya, kita memiliki alasan untuk percaya bahwa populasi 2 dan 3 paling dekat. Populasi 4 dan 5 juga dekat, tetapi tidak sedekat populasi 2 dan 3. Populasi 1 lebih dekat ke populasi 2 dan 3 daripada populasi 4 dan 5.

Kedekatan tersebut digambarkan dalam diagram:

## Warning in knitr::include_graphics("C:/Sem 6/Asprak - Rancob/ModulPrak-Rancob/Gambar/
## formula_59.gif"): It is highly recommended to use relative paths for images. You had absolute
## paths: "C:/Sem 6/Asprak - Rancob/ModulPrak-Rancob/Gambar/formula_59.gif"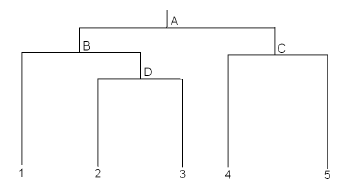

Gambar 3.1: Diagram pengelompokan populasi. Sumber: Department of Statistics, Pennsylvania State University (online.stat.psu.edu).

Dari grafik dan soal tersebut, muncul empat pertanyaan: 1. Apakah populasi 2 dan 3 (yang dianggap sekelompok) beda? (D) 2. Apakah populasi 4 dan 5 beda? (C) 3. Apakah populasi 1 beda dengan populasi 2, 3? (B) 4. Apakah populasi 1, 2, 3, beda dengan populasi 4 dan 5? (A)

Oleh karena itu, dapat dibentuk kontras:

Kontras	1	2	3	4	5
A	2	2	2	-3	-3
B	2	-1	-1	0	0
C	0	0	0	1	-1
D	0	1	-1	0	0

Keortogonalan kontras tersebut dapat dicek melalui matriks ragam peragam:

A<-c(2,2,2,-3,-3)
B<-c(2,-1,-1,0,0)
C<-c(0,0,0,1,-1)
D<-c(0,1,-1,0,0)

contrasts<-cbind(A,B,C,D)
cov(contrasts)

##     A   B   C   D
## A 7.5 0.0 0.0 0.0
## B 0.0 1.5 0.0 0.0
## C 0.0 0.0 0.5 0.0
## D 0.0 0.0 0.0 0.5

Jika matriks diagonal, ini berarti koragam nol dan kontras saling orthogonal. Secara logis, hasil tiap uji tidak memberi informasi mengenai hasil uji lainnya.

Contoh lain untuk mengilustrasikan kontras orthogonal adalah sebagai berikut

Efektivitas suatu obat hendak dicek. Perlakuan 1 merupakan obat A berdosis rendah, perlakuan 2 merupakan obat A berdosis tinggi, perlakuan 3 merupakan obat B berdosis rendah, dan perlakuan 4 merupakan obat B berdosis tinggi.

Tentu, terlihat beberapa arah perbandingan:

Obat - apakah obat A dan B beda?
Dosis - apakah dosis tinggi dan rendah beda?
Interaksi - apakah efek obat bergantung pada dosis?

Sehingga dibuat kontras:

Kontras	1	2	3	4
Obat	1	1	-1	-1
Dosis	1	-1	1	-1
Interaksi	1	-1	-1	1

Cek ortogonalitas

Obat<-c(1,1,-1,-1)
Dosis<-c(1,-1,1,-1)
Interaksi<-c(1,-1,-1,1)

contrasts2<-cbind(Obat,Dosis,Interaksi)
cov(contrasts2)

##               Obat    Dosis Interaksi
## Obat      1.333333 0.000000  0.000000
## Dosis     0.000000 1.333333  0.000000
## Interaksi 0.000000 0.000000  1.333333

Alasan penyusunan kontras obat dan dosis seperti di tabel cukup masuk akal. Bandingkan obat A dan B atau kelompok dosis tinggi dan dosis rendah. Penyusunan kontras interaksi sebenarnya sama saja dengan mengalikan efek-efek sebelumnya. Telah disusun obat A bertanda positif (+) dan obat B bertanda negatif (-). Dosis rendah bertanda positif (+) dan dosis tinggi bertanda negatif. Maka, kalikan saja tanda tersebut.

Sebagai contoh lain, misal diberi tabel rata-rata perlakuan sebagai berikut:

Perlakuan	A	B	C	D
Rata-rata	12.0	12.3	10.8	6.8

Dapat dilihat bahwa D tampak sangat berbeda dari perlakuan lain. A dan B tampak sangat mirip. C agak dekat ke A dan B. Oleh karena itu, susun kontras:

Kontras	A	B	C	D
D vs ABC	1	1	1	-3
c vs AB	1	1	-2	0
A vs B	1	-1	0	0

Orthogonalitas kontras tersebut dapat diuji:

DvABC<-c(1,1,1,-3)
CvAB<-c(1,1,-2,0)
AvB<-c(1,-1,0,0)

contrasts3<-cbind(DvABC,CvAB,AvB)
cov(contrasts3)

##       DvABC CvAB       AvB
## DvABC     4    0 0.0000000
## CvAB      0    2 0.0000000
## AvB       0    0 0.6666667

3.4.2 Menghitung Kontras

Setelah mengetahui cara membuat kontras, bagaimana perhitungannya? Untuk t-1 kontras orthogonal, dapat dilakukan uji F, dengan statistik uji sebagai berikut: \[ \begin{aligned} JKC&=KTC=\frac{\left(\sum_{i=1}^t c_{i}Y_{i.}\right)^2}{r\sum_{i=1}^t c_{i}^2}\\ F&=KTC/KTG=F_{\alpha,1,db_{g}} \end{aligned} \] Dapat dipraktekkan di R:

library(googlesheets4)
dataKontras<-read_sheet("https://docs.google.com/spreadsheets/d/19lOrOm5Vb7ATet8tR6Xq5NEOnB1J2Jj7HXPDy6Sv9og/edit?usp=sharing")

## √ Reading from "Kontras".

## √ Range 'Sheet1'.

knitr::kable(dataKontras)

Perlakuan	Kelompok 1	Kelompok 2	Kelompok 3
Kontrol	9.9	12.3	11.4
Fall	11.4	12.9	12.7
Spring	12.1	13.4	12.9
Split	10.1	12.2	11.9

Tentu, data harus di-melt:

library(reshape2)
KontrasMelted<-melt(dataKontras,
                    id.vars=c("Perlakuan"),
                    measured.vars=c("Kelompok 1", "Kelompok 2","Kelompok 3"),
                    value.name="Pertumbuhan")
colnames(KontrasMelted)[2]<-"Kelompok"

Lalu, pastikan perlakuan dan kelompok adalah faktor dan buat kontras:

#faktor
KontrasMelted$Perlakuan<-as.factor(KontrasMelted$Perlakuan)
KontrasMelted$Kelompok<-as.factor(KontrasMelted$Kelompok)

levels(KontrasMelted$Perlakuan)

## [1] "Fall"    "Kontrol" "Split"   "Spring"

Kita sudah mengetahui urutan faktor di R. Oleh karena itu, buat kontras:

#buat kontras
contrasts(KontrasMelted$Perlakuan) <- cbind(c(1, -3, 1, 1), c(1, 0, 0, -1),
                             c(1, 0, -2, 1))
contrasts(KontrasMelted$Perlakuan)

##         [,1] [,2] [,3]
## Fall       1    1    1
## Kontrol   -3    0    0
## Split      1    0   -2
## Spring     1   -1    1

Lakukan ANOVA dan partisi:

aovKontras<-aov(Pertumbuhan~Perlakuan+Kelompok,KontrasMelted)
summary.aov(aovKontras, split = list (Perlakuan = list('K vs FSpSpl' = 1, 'F vs Sp' = 2, 'FSp vs Spl' = 3)))

##                          Df Sum Sq Mean Sq F value   Pr(>F)    
## Perlakuan                 3  5.200   1.733  19.439 0.001713 ** 
##   Perlakuan: K vs FSpSpl  1  2.151   2.151  24.125 0.002679 ** 
##   Perlakuan: F vs Sp      1  0.327   0.327   3.664 0.104123    
##   Perlakuan: FSp vs Spl   1  2.722   2.722  30.530 0.001480 ** 
## Kelompok                  2  7.172   3.586  40.215 0.000335 ***
## Residuals                 6  0.535   0.089                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretasi dari partisi tersebut sesuai dengan hipotesis yang diuji. Jika menggunakan \(\alpha=5\%\), dinyatakan bahwa rata-rata kontrol dengan perlakuan lainnya berbeda signifikan, begitu juga rata-rata 2 musim dengan 1 musim. Namun, belum ditemukan bukti cukup untuk menyatakan rata-rata musim semi dan gugur berbeda signifikan.

3.5 Polinomial Orthogonal

Polinomial orthogonal dilakukan untuk menguji tren pengaruh perlakuan terhadap respon jika perlakuan bersifat kuantitatif dan berjarak sama. Model polinomial orthogonal dapat berbentuk linear, kuadratik, kubik, kuartik, dan lain-lain:

\[ \begin{aligned} \text{Linear: }& Y_{i}=\beta_0+\beta_1X_i+\varepsilon_i\\ \text{Kuadratik: }& Y_{i}=\beta_0+\beta_1X_i+\beta_2X_i^2+\varepsilon_i\\ \text{Kubik: }& Y_{i}=\beta_0+\beta_1X_i+\beta_2X_i^2+\beta_3X_i^3+\varepsilon_i\\ \end{aligned} \]

Dengan bentuk umum polinomial ordo ke-N adalah:

\[ Y=\alpha_0P_0(X)+\alpha_1P_1(X)+\alpha_2P_2(X)+\ldots+\alpha_nP_n(X)+\varepsilon_i \]

Dengan: \[ \begin{aligned} P_0&=1\\ P_1&=\lambda_1\left[\frac{X-\bar{X}}{d}\right]\\ P_2&=\lambda_2\left[\left(\frac{X-\bar{X}}{d}\right)^2-\left(\frac{a^2-1}{12}\right)\right]\\ P_{n+1}(X)&=\lambda_{n+1}\left[P_1(X)P_n(X)-\frac{n^2(a^2-n^2)}{4(4n^2-1)}P_{n-1}(X)\right] \end{aligned} \]

Dengan:

\(a\): banyaknya taraf faktor
\(d\): jarak antar faktor
\(n\): polinomial ordo ke-n

Tabel kontras bagi polinomial orthogonal untuk a jumlah faktor dapat dihasilkan dengan contr.poly(a):

knitr::kable(contr.poly(5), col.names=c("Linear",
                                        "Kuadratik",
                                        "Kubik",
                                        "Kuartik"))

Linear	Kuadratik	Kubik	Kuartik
-0.6324555	0.5345225	-0.3162278	0.1195229
-0.3162278	-0.2672612	0.6324555	-0.4780914
0.0000000	-0.5345225	0.0000000	0.7171372
0.3162278	-0.2672612	-0.6324555	-0.4780914
0.6324555	0.5345225	0.3162278	0.1195229

Untuk memperlihatkan cara kerja polinomial orthogonal, dapat dibuat suatu data yang memiliki taraf-taraf faktor kuantitatif:

kerapatan <- factor(rep(c(10, 20, 30, 40, 50), each = 3))
hasil <- c(12.2, 11.4, 12.4,
           16.0, 15.5, 16.5, 
           18.6, 20.2, 18.2,
           17.6, 19.3, 17.1,
           18.0, 16.4, 16.6)
data2 <- data.frame(kerapatan, hasil)
str(data2)

## 'data.frame':    15 obs. of  2 variables:
##  $ kerapatan: Factor w/ 5 levels "10","20","30",..: 1 1 1 2 2 2 3 3 3 4 ...
##  $ hasil    : num  12.2 11.4 12.4 16 15.5 16.5 18.6 20.2 18.2 17.6 ...

Sebelum menganalisis menggunakan polinomial, plot data sebagai cara eksploratif:

library(ggplot2)

ggplot(data2,aes(x=kerapatan,y=hasil))+
  geom_point()+
  stat_summary(fun.y=mean, colour="darkblue", geom="line", aes(group = 1))+
  theme_bw()

## Warning: `fun.y` is deprecated. Use `fun` instead.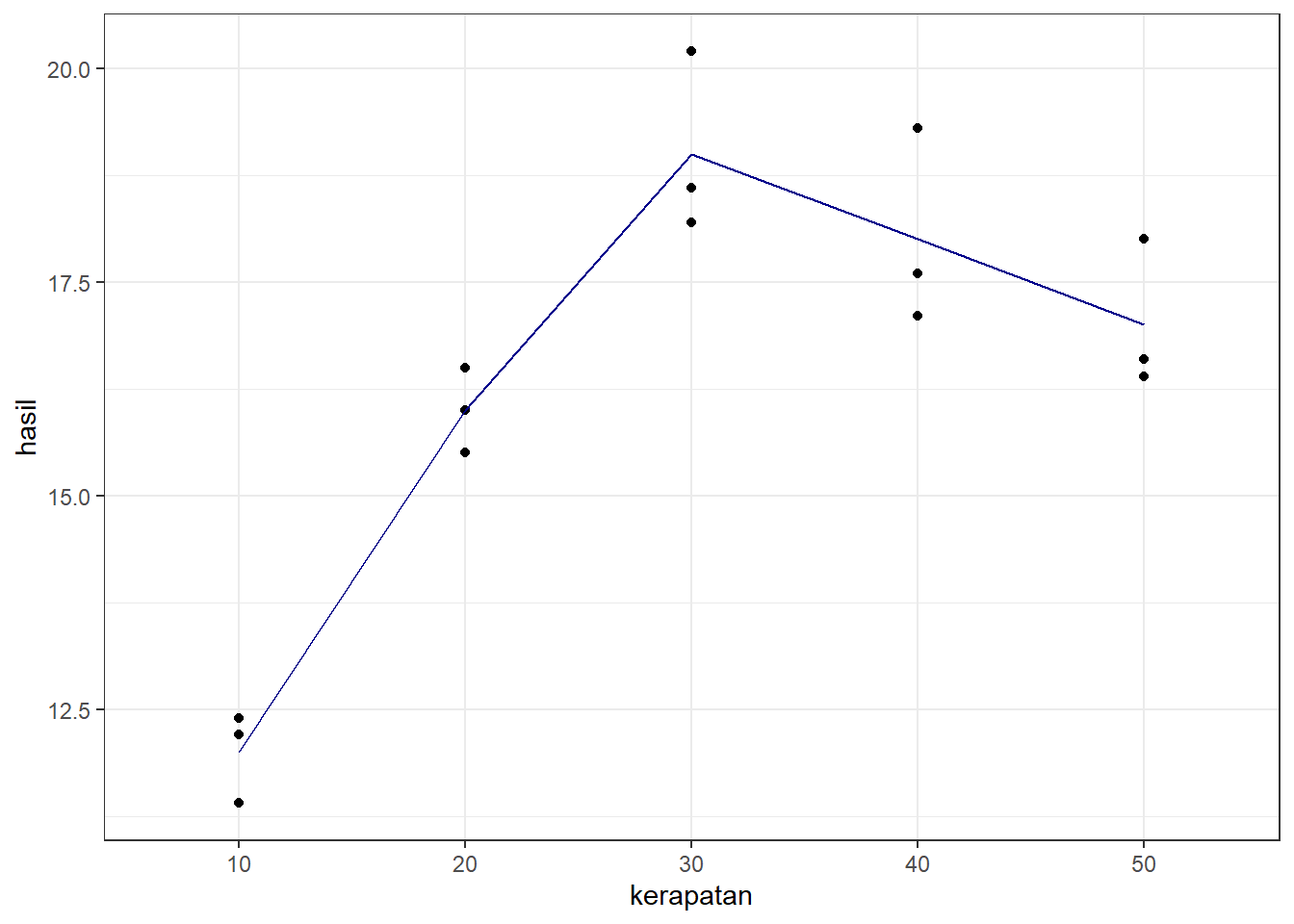

Tampaknya pengaruh kerapatan berbentuk kuadratik karena plot menarik, mencapai puncak, lalu menurun. Lalu, definisikan kontras dan lakukan ANOVA.

contrasts(data2$kerapatan) <- contr.poly(5)

anova2 <- aov(hasil ~ kerapatan, data = data2)
summary.aov(anova2, split = list (kerapatan = list('Linear' = 1, 'Kuadratik' = 2,
                                                    'Kubik' = 3, 'Kuartik' = 4)))

##                        Df Sum Sq Mean Sq F value   Pr(>F)    
## kerapatan               4  87.60   21.90  29.278 1.69e-05 ***
##   kerapatan: Linear     1  43.20   43.20  57.754 1.84e-05 ***
##   kerapatan: Kuadratik  1  42.00   42.00  56.150 2.08e-05 ***
##   kerapatan: Kubik      1   0.30    0.30   0.401    0.541    
##   kerapatan: Kuartik    1   2.10    2.10   2.807    0.125    
## Residuals              10   7.48    0.75                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Nampaknya pengaruh kerpatan pada hasil berupa kuadratik, yang dapat dimodelkan sebagai:

summary(lm(hasil~kerapatan,data2))

## 
## Call:
## lm(formula = hasil ~ kerapatan, data = data2)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -0.90  -0.55  -0.40   0.45   1.30 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  16.4000     0.2233  73.441 5.35e-15 ***
## kerapatan.L   3.7947     0.4993   7.600 1.84e-05 ***
## kerapatan.Q  -3.7417     0.4993  -7.493 2.08e-05 ***
## kerapatan.C   0.3162     0.4993   0.633    0.541    
## kerapatan^4   0.8367     0.4993   1.676    0.125    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8649 on 10 degrees of freedom
## Multiple R-squared:  0.9213, Adjusted R-squared:  0.8899 
## F-statistic: 29.28 on 4 and 10 DF,  p-value: 1.69e-05

\[ Y=16.400+3.7947X_i-3.7417X_i^2 \]

Kontras juga dapat diinput secara manual.