Bab 5 Rancangan Faktorial
Di kebanyakan aplikasi percangan percobaan, ada lebih dari satu faktor yang memengaruhi respon tertentu. Misal, produksi suatu petak tanah ditentukan oleh pemupukan, varietas yang ditanam, irigasi, dan lain-lain. Bahkan, pengujian pengaruh satu faktor belum tentu valid jika level faktor-faktor lain berbeda. Misal, dalam kondisi irigasi yang cukup, varietas yang berbeda akan memiliki produktivitas berbeda. Namun, irigasi yang tidak cukup akan menyebabkan semua varietas mati kekurangan air sehingga produksi semua varietas sama-sama nol. Contoh tersebut cukup ekstrim, tetapi intinya adalah respon merupakan akibat dari berbagai faktor secara simultan, tidak terpisah (interaksi). Belum tentu, misal, tambahan pemumpukan 1 \(kg\) selalu menambah produktivitas 1 \(kg/ha\) - efek tersebut mungkin lebih besar di kondisi tertentu (varietas yang reseptif pada pupuk, irigasi baik). Oleh karena itu, perlu rancangan percobaan dengan lebih dari satu faktor untuk beberapa aplikasi tertentu. Selain itu, semua kombinasi taraf faktor harus dicobakan, karena pengaruh taraf suatu faktor dapat berbeda-beda jika dipasangkan dengan taraf faktor lain yang berbeda.
Note, hal ini berarti faktor-faktor harus bersilang, tidak bersarang. Jika level faktor tertentu hanya muncul saat faktor memiliki level tertentu juga, tidak dapat diuji semua kombinasi perlakuan. Jika saat kerapatan tanaman tinggi, misal, varietas tertentu tidak dapat ditanam, tidak mungkin dilakukan rancangan faktorial.
5.1 Faktorial RAL
5.1.1 Pembuatan bagan percobaan
Karena perlakuan di suatu percobaan faktorial merupakan semua kombinasi taraf faktor yang diteliti, pembuatan bagan percobaan diawali dengan penjabaran taraf-taraf faktor tersebut. Lalu digunakan fungsi expand.grid dari package data.table untuk mengkombinasikan taraf-taraf faktor:
library(data.table)
trt1<-c("A","B","C")
trt2<-c("D","E","F")
perlakuan<-data.frame(expand.grid(trt1,trt2)) #buat kombinasi
colnames(perlakuan)<-c("Faktor 1", "Faktor 2") #penamaan faktor, berupa kosmetik
knitr::kable(perlakuan)| Faktor 1 | Faktor 2 |
|---|---|
| A | D |
| B | D |
| C | D |
| A | E |
| B | E |
| C | E |
| A | F |
| B | F |
| C | F |
Terlihat bahwa tiap baris merupakan kombinasi unik dari taraf faktor satu dan dua. Jumlah baris juga tepat, yaitu \(3 \times 3=9\). Lalu, kode bagi tiap kombinasi tersebut dapat diekstraksi dan dibuat. Tiap kombinasi dapat dikodekan dengan angka, atau dengan teks yang merupakan gabungan dari nama taraf faktor pertama dan kedua.
perlakuan$kode<-seq(1,nrow(perlakuan)) #angka
perlakuan$kode2<-paste(perlakuan$`Faktor 1`,perlakuan$`Faktor 2`,sep="") #gabungan nama taraf; sep=pemisah -> "" berarti tak ada pemisah
knitr::kable(perlakuan)| Faktor 1 | Faktor 2 | kode | kode2 |
|---|---|---|---|
| A | D | 1 | AD |
| B | D | 2 | BD |
| C | D | 3 | CD |
| A | E | 4 | AE |
| B | E | 5 | BE |
| C | E | 6 | CE |
| A | F | 7 | AF |
| B | F | 8 | BF |
| C | F | 9 | CF |
Lalu, buat saja bagan tersebut melalui design.crd (RAL) di library agricolae. Masukkan jumlah ulangan yang diinginkan juga. Akan ditunjukkan sepuluh unit percobaan pertama sebagai ilustrasi:
library(agricolae)
baganFRAL<-design.crd(trt=perlakuan$kode2,r=4,seed=16,serie=0)
#akses output -> hasil design.crd$book
knitr::kable(head(baganFRAL$book,n=10))| plots | r | perlakuan$kode2 |
|---|---|---|
| 1 | 1 | AF |
| 2 | 1 | CD |
| 3 | 1 | BD |
| 4 | 1 | CE |
| 5 | 1 | CF |
| 6 | 1 | AE |
| 7 | 2 | AF |
| 8 | 3 | AF |
| 9 | 2 | CD |
| 10 | 2 | CE |
Dapat diverifikasi bahwa jumlah unit percobaan merupakan \(9 \times 4=36\).
nrow(baganFRAL$book)## [1] 365.1.1.1 Pengacakan edibble
Karena rancangan pengendalian lingkungan berupa RAL, hanya ada satu jenis unit. Lalu, ada dua perlakuan di set_trts yang semuanya dialokasikan ke unit secara bersamaan. Oleh karena itu, tulis c(P1.,P2.) untuk menggabungkan kedua perlakuan, lalu allot_trts(c(P1.,P2.)~unit) untuk mengalokasikan semua kombinasi perlakuan tersebut ke unit.
library(edibble)
desFaktRAL<-design(name="Faktorial RAL") %>%
set_units(unit=36) %>%
set_trts(P1.=trt1,
P2.=trt2) %>%
allot_trts(c(P1.,P2.) ~unit) %>%
assign_trts("random", seed=420) %>% serve_table
knitr::kable(head(desFaktRAL,n=10))| unit | P1. | P2. |
|---|---|---|
| unit1 | C | E |
| unit2 | B | D |
| unit3 | A | E |
| unit4 | C | F |
| unit5 | A | D |
| unit6 | C | F |
| unit7 | A | D |
| unit8 | B | D |
| unit9 | B | F |
| unit10 | A | E |
Lalu, plot-kan:
deggust::autoplot(desFaktRAL)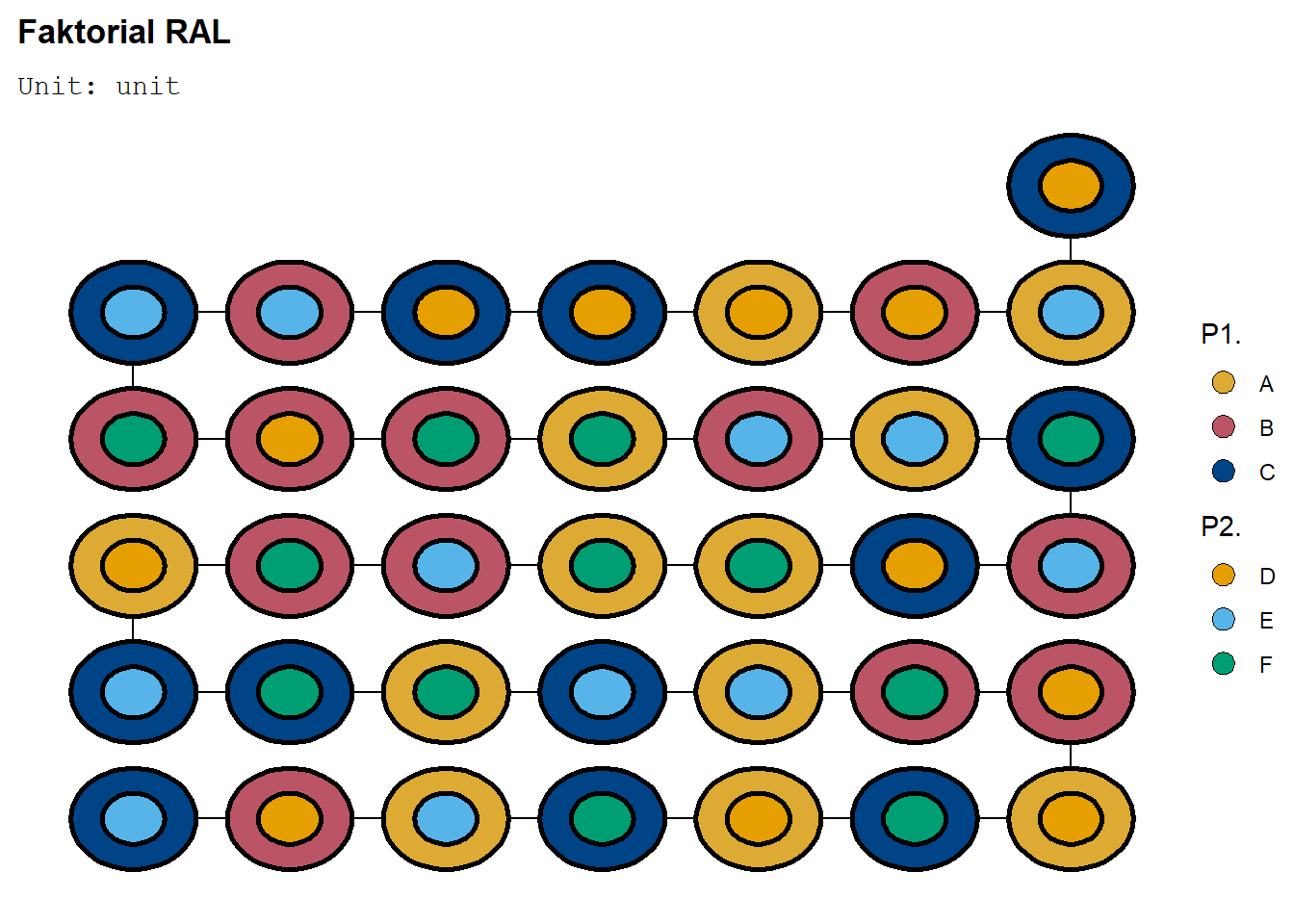
Bandingkan dengan default edibble:
fac <- takeout(menu_factorial(trt = c(3, 3), r=4, seed=420))
examine_recipe(fac)## design("Factorial Design") %>%
## set_units(unit = 36) %>%
## set_trts(trt1 = 3,
## trt2 = 3) %>%
## allot_trts(~unit) %>%
## assign_trts("random", seed = 420) %>%
## serve_table()deggust::autoplot(fac)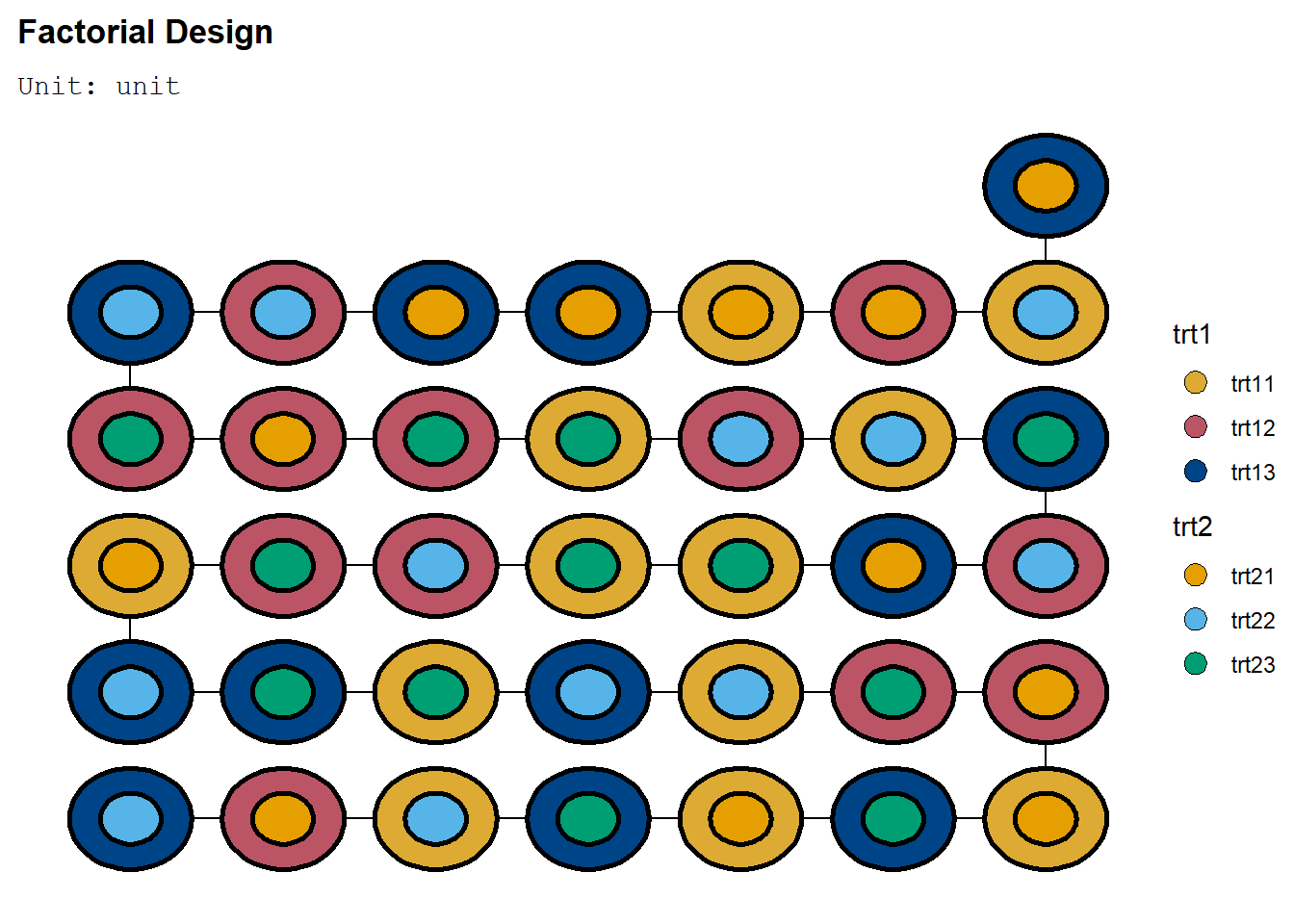
Cara pembuatan dan plot sama di kedua kasus.
5.1.2 Model Linear Aditif
Model bagi faktorial RAL adalah sebagai berikut: \[ y_{ijk}=\mu+\alpha_i+\beta_j+(\alpha\beta)_{ij}+\varepsilon_{ijk} \]
Dengan:
- \(Y_{ijk}\) adalah nilai pengamatan pada faktor A taraf ke-i dan faktor B taraf ke-j pada ulangan ke-k.
- \(\mu\) adalah komponen aditif dari rataan umum.
- \(\alpha_i\) adalah komponen aditif dari pengaruh faktor A pada taraf ke-i.
- \(\beta_j\) adalah komponen aditif dari pengaruh faktor B pada taraf ke-j.
- \((\alpha\beta)_{ij}\) adalah komponen interaksi faktor A dan faktor B.
- \(\varepsilon_{ijk}\sim N(0,\sigma_\varepsilon^2)\) adalah komponen acak pada tiap pengamatan
Oleh karena itu, terdapat tiga hipotesis yang diuji, yaitu hipotesis mengenai pengaruh faktor A, pengaruh faktor B, dan pengaruh interaksi:
$$ \[\begin{align*} &\textbf{Pengaruh faktor A:}\\ H_0&: \alpha_1=\cdots=\alpha_a=0 \text{ (faktor A tidak berpengaruh pada respon yang diamati)}\\ H_1&: \text{paling sedikit ada satu i di mana }\alpha_i\neq0\\ \\ &\textbf{Pengaruh faktor B:}\\ H_0&: \beta_1=\cdots=\beta_b=0 \text{ (faktor B tidak berpengaruh pada respon yang diamati)}\\ H_1&: \text{paling sedikit ada satu j di mana }\beta_j\neq0\\ \\ &\textbf{Pengaruh interaksi:}\\ H_0&: (\alpha\beta)_{11}=(\alpha\beta)_{12}=\cdots=(\alpha\beta)_{ab}=0 \text{ (Interaksi faktor A dan B tidak berpengaruh pada respon yang diamati)}\\ H_1&: \text{paling sedikit ada sepasang } (i,j) \text{ di mana }(\alpha\beta)_{ij}\neq0 \end{align*}\] $$
Hipotesis tersebut diuji dengan uji-F, yang disimpulkan di tabel sidik ragam:
cat('
| Sumber Keragaman| db| JK| KT| F-hit|F(dbP,dbG)|
|------------:|-----------:|------------:|------------:|------------:|------------:|
| A| a-1| JKA| JKP/dbA | KTA/KTG | |
| B| b-1| JKB| JKB/dbB | KTB/KTG | |
| A*B| (a-1)(b-1)| JKAB| JKAB/dbAB | KTAB/KTG | |
| Galat| ab(r-1)| JKG| JKG/dbG | | |
| Total| abr-1| JKT| | | |')##
## | Sumber Keragaman| db| JK| KT| F-hit|F(dbP,dbG)|
## |------------:|-----------:|------------:|------------:|------------:|------------:|
## | A| a-1| JKA| JKP/dbA | KTA/KTG | |
## | B| b-1| JKB| JKB/dbB | KTB/KTG | |
## | A*B| (a-1)(b-1)| JKAB| JKAB/dbAB | KTAB/KTG | |
## | Galat| ab(r-1)| JKG| JKG/dbG | | |
## | Total| abr-1| JKT| | | |Di mana jumlah kuadrat tersebut dihitung dengan: \[ \begin{align*} FK&=\frac{y^2_{...}}{abr}\\ JKT&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(y_{ijk}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r y_{ijk}^2-FK\\ JKA&=\sum_{i=1}^a\left(\bar{y}_{i..}-\bar{y}_{...}\right)^2=\sum_{i=1}^a \frac{y_{i..}^2}{br}-FK\\ JKB&=\sum_{j=1}^b\left(\bar{y}_{.j.}-\bar{y}_{...}\right)^2=\sum_{j=1}^b \frac{y_{.j.}^2}{ar}-FK\\ JKP&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b \frac{y_{ij.}^2}{r}-FK\\ JKAB&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{i..}-\bar{y}_{.j.}+\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2-JKA-JKB\\ &=JKP-JKB-JKA\\ JKG&=JKP-JKT \end{align*} \]
5.1.3 ANOVA dengan R
Akan digunakan kasus berikut dari Mattjik dan Sumertajaya:
Balai Karantina ingin mengetahui pengaruh pemberian fumigasi dengan berbagai dosis (0, 16, 32, 48, 64; \(g/m^3\)) dengan lama fumigasi yang berbeda (2 dan 4 jam) terhadap daya kecambah benih tomat. Metode perkecambahan yang digunakan adalah Growing on Test. Unit percobaan diasumsikan homogen.
Pertama, baca data terlebih dahulu:
library(googlesheets4)
Fact<-read_sheet("https://docs.google.com/spreadsheets/d/1HuYXEBHlpJCXY2v-XJfmiUoFSN05plULDE1T7E1vnPo/edit?usp=sharing")
knitr::kable(Fact)| LamaFumigasi | Ulangan | Dosis Fumigan | …4 | …5 | …6 | …7 |
|---|---|---|---|---|---|---|
| NA | NA | 0 | 16 | 32 | 48 | 64 |
| 2 | 1 | 96 | 92 | 92 | 74 | 50 |
| 2 | 2 | 98 | 88 | 94 | 74 | 50 |
| 2 | 3 | 94 | 90 | 84 | 68 | 54 |
| 4 | 1 | 90 | 88 | 78 | 0 | 0 |
| 4 | 2 | 94 | 92 | 82 | 0 | 0 |
| 4 | 3 | 92 | 94 | 74 | 0 | 0 |
Terlihat bahwa baris pertama merupakan taraf-taraf dari faktor dosis. Oleh karena itu, baris tersebut sebaiknya dihilangkan. Selain itu, kolom ketiga sampai terakhir hendak diberi nama sesuai dosis diberikan.
Fact<-read_sheet("https://docs.google.com/spreadsheets/d/1HuYXEBHlpJCXY2v-XJfmiUoFSN05plULDE1T7E1vnPo/edit?usp=sharing")[-1,]
colnames(Fact)[seq(3,ncol(Fact))]<-seq(0,64,16)Lalu, data tersebut dirubah ke format long di mana tiap baris menunjukkan unit percobaan individu, bukan kombinasi nama ulangan dan dosis fumigasi. Seperti biasa, id.vars merupakan pembeda individu di format wide awal (dalam kasus ini, tiap individu adalah kombinasi LamaFumigasi dan Ulangan). Lalu, value.vars merupakan kolom-kolom yang digabung menjadi satu, dalam kasus ini dosis-dosis dari 0 sampai 64.
library(reshape2)
Fact2<-melt(Fact,
#variabel yang membedakan tiap baris di tabulasi asli:
id.vars=c("LamaFumigasi","Ulangan"),
value.vars=seq(0,64,16),
value.name="Perkecambahan")
colnames(Fact2)[3]<-"Dosis" #kolom ketiga akan disebut "variable"Setelah tabulasi data benar, pastikan tiap faktor sudah dibuat menjadi objek data yang benar; lakukan ANOVA dan lihat hasil:
Fact2$LamaFumigasi<-as.factor(Fact2$LamaFumigasi)
Fact2$Dosis<-as.factor(Fact2$Dosis)
aovFact<-aov(Perkecambahan~LamaFumigasi+Dosis+LamaFumigasi:Dosis,Fact2)
summary(aovFact)## Df Sum Sq Mean Sq F value Pr(>F)
## LamaFumigasi 1 5713 5713 691.1 < 2e-16 ***
## Dosis 4 25459 6365 769.9 < 2e-16 ***
## LamaFumigasi:Dosis 4 6258 1565 189.3 1.37e-15 ***
## Residuals 20 165 8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Analisis di python dapat dilakukan dengan membaca CSV dan mengambil row ke-2 sampai akhir. Note bahwa indeks di Python dimulai dari 0, sehingga baris ke-2 dinotasikan dengan 1.
fum=pd.read_csv("https://docs.google.com/spreadsheets/d/1HuYXEBHlpJCXY2v-XJfmiUoFSN05plULDE1T7E1vnPo/export?gid=0&format=csv")
fumn=fum.iloc[1:]Lalu, ubah nama kolom:
print(fumn.columns)## Index(['LamaFumigasi', 'Ulangan', 'Dosis Fumigan', 'Unnamed: 3', 'Unnamed: 4',
## 'Unnamed: 5', 'Unnamed: 6'],
## dtype='object')Ambil elemen pertama dan kedua (0, 1) - indexing di Python dimulai dari 0 dan berakhir di elemen \(n-1\) sehingga ambil elemen [0:2]. Elemen tersebut diubah menjadi list. Lalu tambahkan angka 0, 16, 32, 48, 64 kepada list tersebut. Lalu masukkan list tersebut ke kolom-kolom dataset:
fumn.columns=list(fumn.columns[0:2])+[str(x) for x in range(0,80,16)]
fumn.head()## LamaFumigasi Ulangan 0 16 32 48 64
## 1 2.0 1.0 96 92 92 74 50
## 2 2.0 2.0 98 88 94 74 50
## 3 2.0 3.0 94 90 84 68 54
## 4 4.0 1.0 90 88 78 0 0
## 5 4.0 2.0 94 92 82 0 0Melt data:
FaktRALMelt=pd.melt(fumn, id_vars=['LamaFumigasi','Ulangan'], value_vars=[str(x) for x in range(0,80,16)])Lakukan ANOVA. Gunakan * untuk mendapat interaksi, dan C() untuk membuat peubah kategorik:
import statsmodels.api as sm
from statsmodels.formula.api import ols
FaktRALlm= ols('value ~ C(LamaFumigasi)*C(variable)',data=FaktRALMelt)
fitRAL=FaktRALlm.fit()
table = sm.stats.anova_lm(fitRAL)
print(table)## df sum_sq ... F PR(>F)
## C(LamaFumigasi) 1.0 5713.200000 ... 691.112903 5.527620e-17
## C(variable) 4.0 25459.200000 ... 769.935484 1.367358e-21
## C(LamaFumigasi):C(variable) 4.0 6258.133333 ... 189.258065 1.370943e-15
## Residual 20.0 165.333333 ... NaN NaN
##
## [4 rows x 5 columns]5.1.4 Tabel dan Plot Interaksi
Sekarang, dapat dicari rata-rata pengaruh perlakuan di tiap kombinasi faktor A dan B. Fungsi yang akan digunakan adalah aggregate dari base R. Argumen pertama merupakan fungsi agregasi yang ingin dilakukan - sintaks ini mirip dengan aov atau lm (respon~perlakuan), argumen kedua merupakan faktor, dan argumen terakhir merupakan fungsi agregasi yang dipakai (dalam kasus ini, mean):
knitr::kable(aggregate(Perkecambahan~Dosis+LamaFumigasi,data=Fact2,FUN=mean))| Dosis | LamaFumigasi | Perkecambahan |
|---|---|---|
| 0 | 2 | 96.00000 |
| 16 | 2 | 90.00000 |
| 32 | 2 | 90.00000 |
| 48 | 2 | 72.00000 |
| 64 | 2 | 51.33333 |
| 0 | 4 | 92.00000 |
| 16 | 4 | 91.33333 |
| 32 | 4 | 78.00000 |
| 48 | 4 | 0.00000 |
| 64 | 4 | 0.00000 |
Lalu, buat tiap baris menjadi taraf faktor A (Lama Fumigasi), dan tiap kolom menjadi taraf faktor B. Gunakan fungsi dcast, dengan sintaks dcast(tabel, fungsi: baris~kolom, peubah respon).
SumTab<-reshape2::dcast(aggregate(Perkecambahan~Dosis+LamaFumigasi,data=Fact2,FUN=mean),LamaFumigasi~Dosis,value.var="Perkecambahan") #(tabel: agregasi, fungsi: baris~kolom)
knitr::kable(SumTab)| LamaFumigasi | 0 | 16 | 32 | 48 | 64 |
|---|---|---|---|---|---|
| 2 | 96 | 90.00000 | 90 | 72 | 51.33333 |
| 4 | 92 | 91.33333 | 78 | 0 | 0.00000 |
Lalu, tambahkan rerata tiap baris (rowMeans). Namun, kolom pertama (lama fumigasi) tidak merupakan peubah respon dan tidak diperhitungkan:
SumTab$Rerata<-rowMeans(SumTab[,-1])
knitr::kable(SumTab)| LamaFumigasi | 0 | 16 | 32 | 48 | 64 | Rerata |
|---|---|---|---|---|---|---|
| 2 | 96 | 90.00000 | 90 | 72 | 51.33333 | 79.86667 |
| 4 | 92 | 91.33333 | 78 | 0 | 0.00000 | 52.26667 |
Lalu, tambahkan rerata per kolom:
SumTab<-rbind(SumTab,colMeans(SumTab[,-1]))## Warning in `[<-.factor`(`*tmp*`, ri, value = 94): invalid factor level, NA generatedknitr::kable(SumTab)| LamaFumigasi | 0 | 16 | 32 | 48 | 64 | Rerata |
|---|---|---|---|---|---|---|
| 2 | 96.00000 | 90.00000 | 90 | 72.00000 | 51.33333 | 79.86667 |
| 4 | 92.00000 | 91.33333 | 78 | 0.00000 | 0.00000 | 52.26667 |
| NA | 90.66667 | 84.00000 | 36 | 25.66667 | 66.06667 | 94.00000 |
Tabel rata-rata perlakuan telah terbentuk. Tabel ini dapat digunakan untuk pembuatan plot interaksi secara manual. Di R, plot interaksi dibuat dengan:
interaction.plot(Fact2$Dosis, Fact2$LamaFumigasi, Fact2$Perkecambahan) #(faktor 1, faktor 2, respon)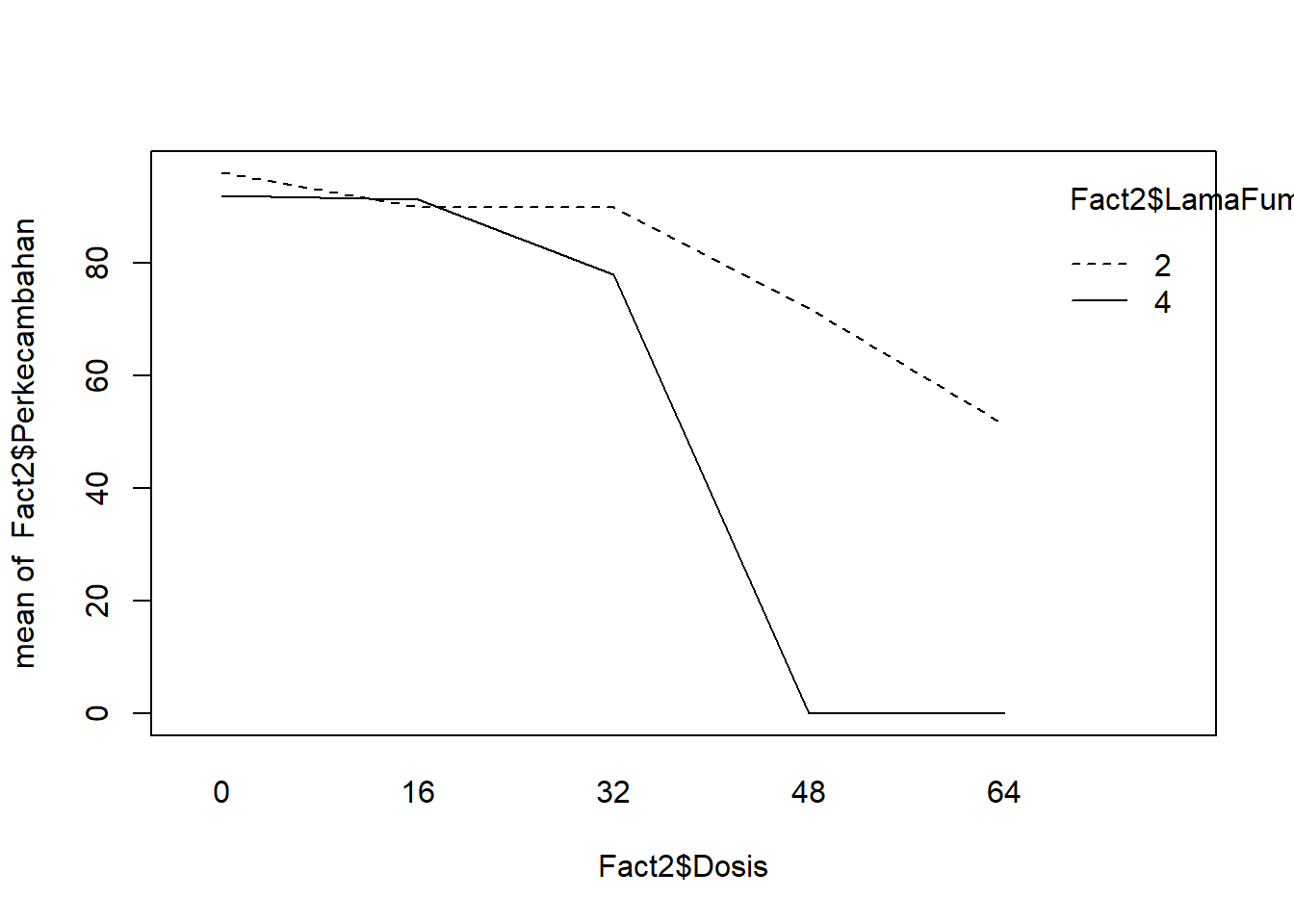
Atau, dapat dibuat plot interaksi melalui library phia. Library phia hanya menerima input berupa lm - ubah olah data menggunakan lm terlebih dahulu. Phia menyediakan tabel rata-rata perlakuan, serta dapat di-plotkan menjadi plot interaksi.
library(phia)
mod<-lm(Perkecambahan~LamaFumigasi+Dosis+LamaFumigasi:Dosis,data=Fact2)
im=interactionMeans(mod)
knitr::kable(im) # tabel| LamaFumigasi | Dosis | adjusted mean | std. error |
|---|---|---|---|
| 2 | 0 | 96.00000 | 1.659987 |
| 4 | 0 | 92.00000 | 1.659987 |
| 2 | 16 | 90.00000 | 1.659987 |
| 4 | 16 | 91.33333 | 1.659987 |
| 2 | 32 | 90.00000 | 1.659987 |
| 4 | 32 | 78.00000 | 1.659987 |
| 2 | 48 | 72.00000 | 1.659987 |
| 4 | 48 | 0.00000 | 1.659987 |
| 2 | 64 | 51.33333 | 1.659987 |
| 4 | 64 | 0.00000 | 1.659987 |
plot(im) # plot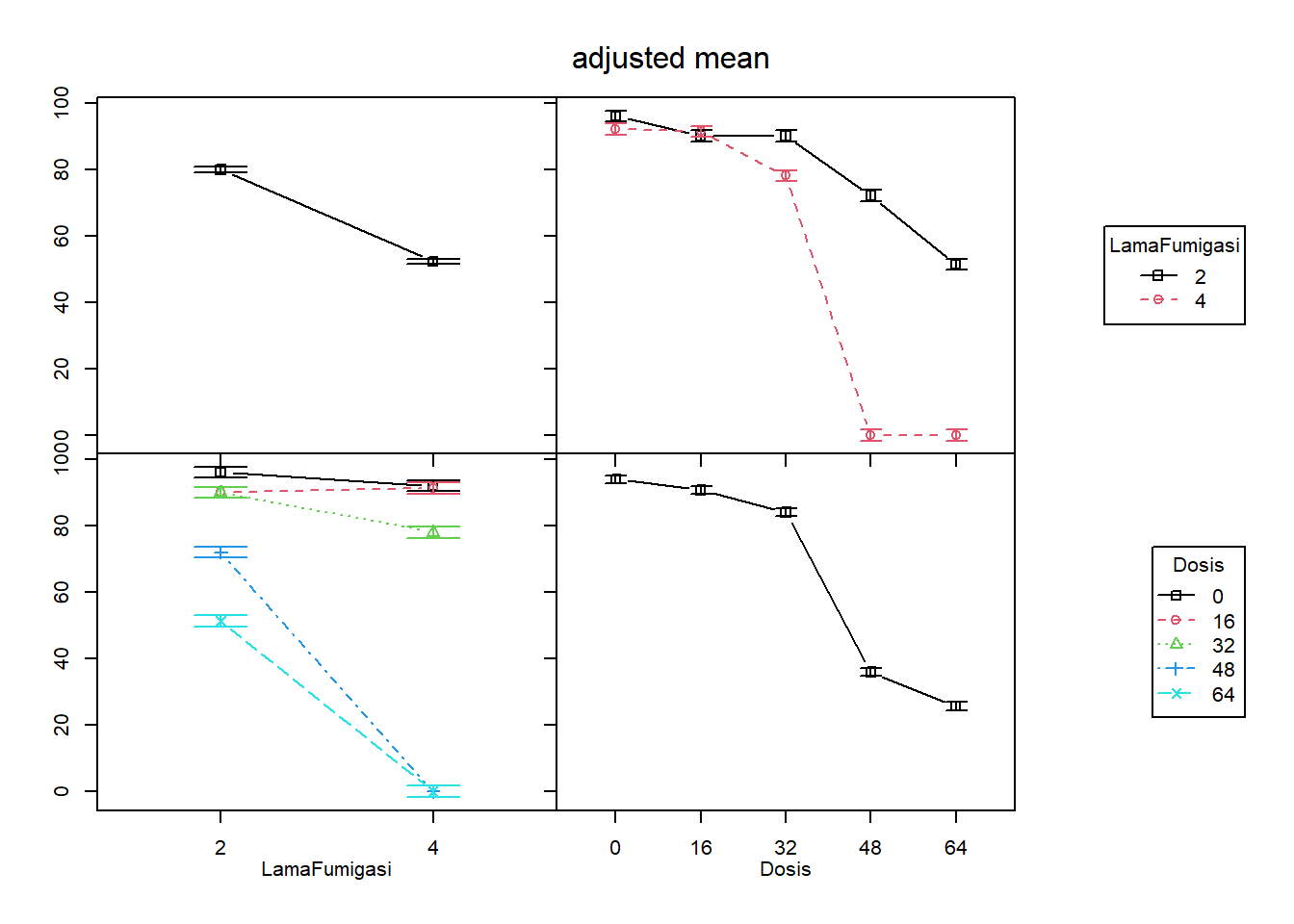
5.1.5 Uji lanjut
Uji lanjut dapat dilakukan dengan library emmeans. Pada dasarnya, emmeans menghasilkan output yang mirip dengan uji lanjut seperti TukeyHSD:
library(emmeans)
marginal = emmeans(mod,~ LamaFumigasi:Dosis)
knitr::kable(head(pairs(marginal,adjust="Tukey"),n=5))| contrast | estimate | SE | df | t.ratio | p.value |
|---|---|---|---|---|---|
| 2 0 - 4 0 | 4 | 2.347576 | 20 | 1.703885 | 0.1038913 |
knitr::kable(head(TukeyHSD(aovFact, conf.level=.95)$`LamaFumigasi:Dosis`),n=5) #metode tukey, tapi bisa saja cara lain seperti bonferroni| diff | lwr | upr | p adj | |
|---|---|---|---|---|
| 4:0-2:0 | -4.000000 | -12.31302 | 4.313018 | 0.7813125 |
| 2:16-2:0 | -6.000000 | -14.31302 | 2.313018 | 0.2987279 |
| 4:16-2:0 | -4.666667 | -12.97968 | 3.646352 | 0.6158480 |
| 2:32-2:0 | -6.000000 | -14.31302 | 2.313018 | 0.2987279 |
| 4:32-2:0 | -18.000000 | -26.31302 | -9.686982 | 0.0000082 |
| 2:48-2:0 | -24.000000 | -32.31302 | -15.686982 | 0.0000001 |
Urutan pengurangannya berbeda saja, sehingga hasil emmeans memiliki beda positif dan TukeyHSD memiliki beda negatif. Library multcomp memiliki output yang lebih rapi, yaitu langsung berupa pengelompokan:
library(multcomp)## Loading required package: mvtnorm## Loading required package: survival## Loading required package: TH.data## Loading required package: MASS##
## Attaching package: 'MASS'## The following object is masked from 'package:dplyr':
##
## select##
## Attaching package: 'TH.data'## The following object is masked from 'package:MASS':
##
## geyserknitr::kable(cld(marginal,
alpha=0.05,
Letters=letters,
adjust="tukey"))## Note: adjust = "tukey" was changed to "sidak"
## because "tukey" is only appropriate for one set of pairwise comparisons| LamaFumigasi | Dosis | emmean | SE | df | lower.CL | upper.CL | .group | |
|---|---|---|---|---|---|---|---|---|
| 8 | 4 | 48 | 0.00000 | 1.659987 | 20 | -5.21784 | 5.21784 | a |
| 10 | 4 | 64 | 0.00000 | 1.659987 | 20 | -5.21784 | 5.21784 | a |
| 9 | 2 | 64 | 51.33333 | 1.659987 | 20 | 46.11549 | 56.55117 | b |
| 7 | 2 | 48 | 72.00000 | 1.659987 | 20 | 66.78216 | 77.21784 | c |
| 6 | 4 | 32 | 78.00000 | 1.659987 | 20 | 72.78216 | 83.21784 | c |
| 3 | 2 | 16 | 90.00000 | 1.659987 | 20 | 84.78216 | 95.21784 | d |
| 5 | 2 | 32 | 90.00000 | 1.659987 | 20 | 84.78216 | 95.21784 | d |
| 4 | 4 | 16 | 91.33333 | 1.659987 | 20 | 86.11549 | 96.55117 | d |
| 2 | 4 | 0 | 92.00000 | 1.659987 | 20 | 86.78216 | 97.21784 | d |
| 1 | 2 | 0 | 96.00000 | 1.659987 | 20 | 90.78216 | 101.21784 | d |
Selain itu, dapat diuji kontras orthogonal dari data ini. Karena hanya ada dua taraf untuk lama fumigasi, kontras hanya dapat dibuat untuk dosis. Misal dibuat kontras untuk membandingkan pengaruh ada dosis (dosis 0 vs lainnya), dosis rendah vs tinggi (16,32 vs 48,64), serta perbandingan antara dosis 16 vs 32 dan 48 vs 64:
levels(Fact2$Dosis)## [1] "0" "16" "32" "48" "64"contrasts(Fact2$Dosis)<- cbind(c(1, -1/4, -1/4, -1/4,-1/4), c(0, 1/2,1/2, -1/2, -1/2),
c(0, 1,-1, 0, 0), c(0,0,0,1,-1))
contrasts(Fact2$Dosis)## [,1] [,2] [,3] [,4]
## 0 1.00 0.0 0 0
## 16 -0.25 0.5 1 0
## 32 -0.25 0.5 -1 0
## 48 -0.25 -0.5 0 1
## 64 -0.25 -0.5 0 -1aovFact1<-aov(Perkecambahan~LamaFumigasi+Dosis+LamaFumigasi:Dosis,Fact2)
summary.aov(aovFact1,split=list(Dosis=list("0 vs ada"=1,"16,32 vs 48,64"=2,"16 vs 32"=3,"48 vs 64"=4)))## Df Sum Sq Mean Sq F value Pr(>F)
## LamaFumigasi 1 5713 5713 691.11 < 2e-16 ***
## Dosis 4 25459 6365 769.93 < 2e-16 ***
## Dosis: 0 vs ada 1 5852 5852 707.91 < 2e-16 ***
## Dosis: 16,32 vs 48,64 1 19154 19154 2316.96 < 2e-16 ***
## Dosis: 16 vs 32 1 133 133 16.13 0.000678 ***
## Dosis: 48 vs 64 1 320 320 38.75 4.43e-06 ***
## LamaFumigasi:Dosis 4 6258 1565 189.26 1.37e-15 ***
## LamaFumigasi:Dosis: 0 vs ada 1 1044 1044 126.33 4.28e-10 ***
## LamaFumigasi:Dosis: 16,32 vs 48,64 1 4760 4760 575.83 3.25e-16 ***
## LamaFumigasi:Dosis: 16 vs 32 1 133 133 16.13 0.000678 ***
## LamaFumigasi:Dosis: 48 vs 64 1 320 320 38.75 4.43e-06 ***
## Residuals 20 165 8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Dapat juga dibuat polinomial orthogonal, dengan koefisien-koefisien sesuai yang ditentukan saat taraf faktor tersebut 4.
contrasts(Fact2$Dosis) <- cbind(c(-2, -1, 0, 1, 2), c(2, -1, -2, -1, 2),
c(-1, 2, 0, -2, 1), c(1, -4, 6, -4, 1))
contrasts(Fact2$Dosis)## [,1] [,2] [,3] [,4]
## 0 -2 2 -1 1
## 16 -1 -1 2 -4
## 32 0 -2 0 6
## 48 1 -1 -2 -4
## 64 2 2 1 1aovFact2<-aov(Perkecambahan~LamaFumigasi+Dosis+LamaFumigasi:Dosis,Fact2)
summary.aov(aovFact2,split=list(Dosis=list("Linear"=1,"Kuadratik"=2,"Kubik"=3,"Kuartik"=4)))## Df Sum Sq Mean Sq F value Pr(>F)
## LamaFumigasi 1 5713 5713 691.113 < 2e-16 ***
## Dosis 4 25459 6365 769.935 < 2e-16 ***
## Dosis: Linear 1 21965 21965 2657.065 < 2e-16 ***
## Dosis: Kuadratik 1 1312 1312 158.733 5.72e-11 ***
## Dosis: Kubik 1 1009 1009 122.008 5.79e-10 ***
## Dosis: Kuartik 1 1173 1173 141.937 1.54e-10 ***
## LamaFumigasi:Dosis 4 6258 1565 189.258 1.37e-15 ***
## LamaFumigasi:Dosis: Linear 1 4234 4234 512.129 1.01e-15 ***
## LamaFumigasi:Dosis: Kuadratik 1 27 27 3.318 0.0835 .
## LamaFumigasi:Dosis: Kubik 1 1480 1480 179.040 1.94e-11 ***
## LamaFumigasi:Dosis: Kuartik 1 517 517 62.545 1.39e-07 ***
## Residuals 20 165 8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 15.2 Faktorial RAKL
Jika kondisi unit percobaan tidak sepenuhnya homogen, dapat digunakan Faktorial RAKL. Sama seperti RAKL pada kasus satu faktor, tiap perlakuan diacak dan diulang sekali di tiap kelompok.
5.2.1 Pengacakan
Pertama, buat tiap kombinasi perlakuan:
library(data.table)
vari<-c("V1","V2","V3")
pupu<-c("N0","N1","N2","N3")
KLperlakuan<-expand.grid(vari,pupu) #buat kombinasi
colnames(KLperlakuan)<-c("Varietas","Pupuk") #ubah nama kolom
knitr::kable(KLperlakuan)| Varietas | Pupuk |
|---|---|
| V1 | N0 |
| V2 | N0 |
| V3 | N0 |
| V1 | N1 |
| V2 | N1 |
| V3 | N1 |
| V1 | N2 |
| V2 | N2 |
| V3 | N2 |
| V1 | N3 |
| V2 | N3 |
| V3 | N3 |
Lalu, beri penomoran bagi tiap kombinasi perlakuan tersebut:
KLperlakuan$Nomor<-paste(KLperlakuan$Varietas,KLperlakuan$Pupuk,sep="")
knitr::kable(KLperlakuan)| Varietas | Pupuk | Nomor |
|---|---|---|
| V1 | N0 | V1N0 |
| V2 | N0 | V2N0 |
| V3 | N0 | V3N0 |
| V1 | N1 | V1N1 |
| V2 | N1 | V2N1 |
| V3 | N1 | V3N1 |
| V1 | N2 | V1N2 |
| V2 | N2 | V2N2 |
| V3 | N2 | V3N2 |
| V1 | N3 | V1N3 |
| V2 | N3 | V2N3 |
| V3 | N3 | V3N3 |
Dari tiap perlakuan tersebut, lakukan pengacakan di tiap kelompok. Di R, ini dilakukan dengan design.rcbd dari agricolae:
library(agricolae)
baganFakt_RAKL<-design.rcbd(KLperlakuan$Nomor,3,seed=78) #kombinasi perlakuan, jml kelompok
knitr::kable(baganFakt_RAKL$sketch)| V1N3 | V2N3 | V2N2 | V2N0 | V2N1 | V1N1 | V3N0 | V3N2 | V3N1 | V1N0 | V3N3 | V1N2 |
| V2N3 | V3N2 | V1N0 | V1N1 | V3N0 | V1N3 | V2N2 | V2N1 | V3N1 | V1N2 | V3N3 | V2N0 |
| V3N0 | V3N2 | V2N3 | V2N1 | V2N2 | V1N0 | V2N0 | V1N2 | V3N1 | V1N3 | V3N3 | V1N1 |
5.2.1.1 Pengacakan edibble
Pada dasarnya, struktur perlakuan akan sama, tetapi struktur unit dibuat sesuai dengan RAKL, yaitu membuat unit kelompok dan petak yang nested_in(kelompok). Perlakuan masih diacak ke petak (unit):
desFaktRAKL<-design(name="Faktorial RAKL") %>%
set_units(kelompok=3,
petak=nested_in(kelompok, 12)) %>%
set_trts(varietas=vari,
pupuk=pupu) %>%
allot_trts(c(varietas,pupuk)~petak) %>%
assign_trts("random", seed=420) %>% serve_table
knitr::kable(head(desFaktRAKL,n=10))| kelompok | petak | varietas | pupuk |
|---|---|---|---|
| kelompok1 | petak1 | V3 | N0 |
| kelompok1 | petak2 | V1 | N1 |
| kelompok1 | petak3 | V3 | N3 |
| kelompok1 | petak4 | V2 | N0 |
| kelompok1 | petak5 | V1 | N0 |
| kelompok1 | petak6 | V1 | N2 |
| kelompok1 | petak7 | V2 | N2 |
| kelompok1 | petak8 | V2 | N3 |
| kelompok1 | petak9 | V1 | N3 |
| kelompok1 | petak10 | V2 | N1 |
Plot dari rancangan tersebut dapat dilihat:
deggust::autoplot(desFaktRAKL)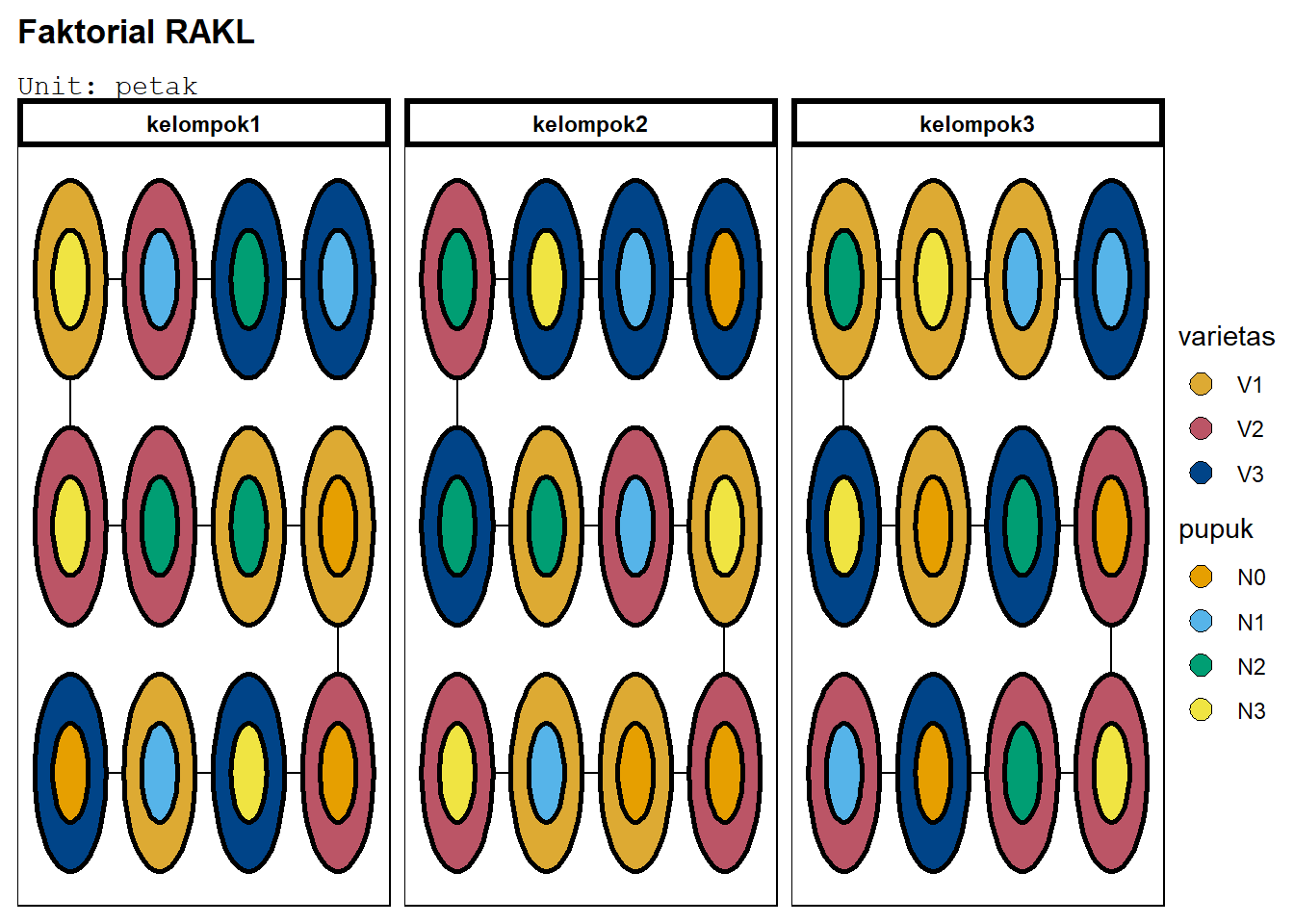
5.2.2 Model Linear Aditif
Model bagi faktorial RAL adalah sebagai berikut: \[ y_{ijk}=\mu+\alpha_i+\beta_j+(\alpha\beta)_{ij}+\rho_k+\varepsilon_{ijk} \]
Dengan:
- \(Y_{ijk}\) adalah nilai pengamatan pada faktor A taraf ke-i dan faktor B taraf ke-j pada ulangan ke-k.
- \(\mu\) adalah komponen aditif dari rataan umum.
- \(\alpha_i\) adalah komponen aditif dari pengaruh faktor A pada taraf ke-i.
- \(\beta_j\) adalah komponen aditif dari pengaruh faktor B pada taraf ke-j.
- \((\alpha\beta)_{ij}\) adalah komponen interaksi faktor A dan faktor B.
- \(\rho_k\) adalah pengaruh aditif dari kelompok dan diasumsikan tidak berinteraksi dengan perlakuan (bersifat aditif) / pengaruh kelompok ke-k
- \(\varepsilon_{ijk}\sim N(0,\sigma_\varepsilon^2)\) adalah komponen acak pada tiap pengamatan
Oleh karena itu, terdapat empat hipotesis yang diuji, yaitu hipotesis mengenai pengaruh faktor A, pengaruh faktor B, pengaruh interaksi, dan pengaruh kelompok:
$$ \[\begin{align*} &\textbf{Pengaruh faktor A:}\\ H_0&: \alpha_1=\cdots=\alpha_a=0 \text{ (faktor A tidak berpengaruh pada respon yang diamati)}\\ H_1&: \text{paling sedikit ada satu i di mana }\alpha_i\neq0\\ \\ &\textbf{Pengaruh faktor B:}\\ H_0&: \beta_1=\cdots=\beta_b=0 \text{ (faktor B tidak berpengaruh pada respon yang diamati)}\\ H_1&: \text{paling sedikit ada satu j di mana }\beta_j\neq0\\ \\ &\textbf{Pengaruh interaksi:}\\ H_0&: (\alpha\beta)_{11}=(\alpha\beta)_{12}=\cdots=(\alpha\beta)_{ab}=0 \text{ (Interaksi faktor A dan B tidak berpengaruh pada respon yang diamati)}\\ H_1&: \text{paling sedikit ada sepasang } (i,j) \text{ di mana }(\alpha\beta)_{ij}\neq0\\ \\ &\textbf{Pengaruh pengelompokan:}\\ H_0&: \rho_1=\cdots=\rho_r=0 \text{ (blok tidak berpengaruh pada respon yang diamati)}\\ H_1&: \text{paling sedikit ada satu k di mana }\rho_k\neq0\\ \\ \end{align*}\] $$
Hipotesis tersebut diuji dengan uji-F, yang disimpulkan di tabel sidik ragam:
| Sumber Keragaman | db | JK | KT | F-hit | F(dbP,dbG) |
|---|---|---|---|---|---|
| A | a-1 | JKA | JKP/dbA | KTA/KTG | |
| B | b-1 | JKB | JKB/dbB | KTB/KTG | |
| A*B | (a-1)(b-1) | JKAB | JKAB/dbAB | KTAB/KTG | |
| Blok | (r-1) | JKK | JKK/dbK | ||
| Galat | (ab-1)(r-1) | JKG | JKG/dbG | ||
| Total | abr-1 | JKT |
Jumlah kuadrat tersebut dihitung dengan: \[ \begin{align*} FK&=\frac{y^2_{...}}{abr}\\ JKT&=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r\left(y_{ijk}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r y_{ijk}^2-FK\\ JKA&=\sum_{i=1}^a\left(\bar{y}_{i..}-\bar{y}_{...}\right)^2=\sum_{i=1}^a \frac{y_{i..}^2}{br}-FK\\ JKB&=\sum_{j=1}^b\left(\bar{y}_{.j.}-\bar{y}_{...}\right)^2=\sum_{j=1}^b \frac{y_{.j.}^2}{ar}-FK\\ JKP&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b \frac{y_{ij.}^2}{r}-FK\\ JKAB&=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{i..}-\bar{y}_{.j.}+\bar{y}_{...}\right)^2=\sum_{i=1}^a\sum_{j=1}^b\left(\bar{y}_{ij.}-\bar{y}_{...}\right)^2-JKA-JKB\\ &=JKP-JKB-JKA\\ JKK&=\sum_{k=1}^r \left(\bar{y}_{..k}-\bar{y}_{...}\right)^2=\sum_{k=1}^r \frac{y_{..k}^2}{ab}-FK\\ JKG&=JKP-JKK-JKT \end{align*} \]
5.2.3 ANOVA dengan R
Seorang peneliti akan melakukan percobaan pada sebuah tanaman dengan mengamati pertumbuhan tinggi tanaman di sebuah green house. Tanaman diberikan 2 jenis perlakuan yang pertama adalah jenis varietas yang terdiri dari Varietas 1(V1), Varietas 2(V2), dan Varietas 3(V3) dan perlakuan kedua adalah dosis pupuk terdiri dari N1, N2, N3, N4, N5. Percobaan ini dilakukan di 3 spot berbeda. Rancangan apakah yang sebaiknya digunakan peneliti? Bagaimana alur percobaan jika dilakukan sesuai rancangan yang anda sarankan? Lalu uji apakah perlakuan yang dicobakan berpengaruh signifikan, jika didapatkan data seperti dibawah ini?
Karena percobaan dilakukan di tiga spot berebeda, maka rancangan adalah faktorial RAKL. Ambil data:
library(googlesheets4)
FactRAKL<-read_sheet("https://docs.google.com/spreadsheets/d/1PqOsMGjb6aBwF-3NsWxsXk3-eevUJBq6sGMGHMLct-A/edit?usp=sharing")
knitr::kable(FactRAKL)| Varietas | kelompok | N1 | N2 | N3 | N4 | N5 |
|---|---|---|---|---|---|---|
| V1 | 1 | 0.9 | 1.2 | 1.3 | 1.8 | 1.1 |
| V1 | 2 | 0.9 | 1.3 | 1.5 | 1.9 | 1.4 |
| V1 | 3 | 1.0 | 1.2 | 1.4 | 2.1 | 1.2 |
| V2 | 1 | 0.9 | 1.1 | 1.3 | 1.6 | 1.9 |
| V2 | 2 | 0.8 | 0.9 | 1.5 | 1.3 | 1.6 |
| V2 | 3 | 0.8 | 0.9 | 1.1 | 1.1 | 1.5 |
| V3 | 1 | 0.9 | 1.4 | 1.3 | 1.4 | 1.2 |
| V3 | 2 | 1.0 | 1.2 | 1.4 | 1.5 | 1.1 |
| V3 | 3 | 0.7 | 1.0 | 1.4 | 1.4 | 1.3 |
Lalu, melt data frame tersebut. Seperti biasa, id.vars merupakan pembeda individu di format wide yang menjadi bentuk awal data frame (dalam kasus ini, tiap individu adalah kombinasi Varietas dan Kelompok). Lalu, value.vars merupakan kolom-kolom yang digabung menjadi satu, dalam kasus ini pupuk dari N1 sampai N5.
library(reshape2)
FactRAKL2<-melt(FactRAKL,
#variabel yang membedakan tiap baris di tabulasi asli:
id.vars=c("Varietas","kelompok"),
value.vars=c("N1","N2","N3","N4","N5"),
value.name="Tinggi")
colnames(FactRAKL2)[3]<-"Pupuk" #kolom ketiga akan disebut "variable"
knitr::kable(FactRAKL2)| Varietas | kelompok | Pupuk | Tinggi |
|---|---|---|---|
| V1 | 1 | N1 | 0.9 |
| V1 | 2 | N1 | 0.9 |
| V1 | 3 | N1 | 1.0 |
| V2 | 1 | N1 | 0.9 |
| V2 | 2 | N1 | 0.8 |
| V2 | 3 | N1 | 0.8 |
| V3 | 1 | N1 | 0.9 |
| V3 | 2 | N1 | 1.0 |
| V3 | 3 | N1 | 0.7 |
| V1 | 1 | N2 | 1.2 |
| V1 | 2 | N2 | 1.3 |
| V1 | 3 | N2 | 1.2 |
| V2 | 1 | N2 | 1.1 |
| V2 | 2 | N2 | 0.9 |
| V2 | 3 | N2 | 0.9 |
| V3 | 1 | N2 | 1.4 |
| V3 | 2 | N2 | 1.2 |
| V3 | 3 | N2 | 1.0 |
| V1 | 1 | N3 | 1.3 |
| V1 | 2 | N3 | 1.5 |
| V1 | 3 | N3 | 1.4 |
| V2 | 1 | N3 | 1.3 |
| V2 | 2 | N3 | 1.5 |
| V2 | 3 | N3 | 1.1 |
| V3 | 1 | N3 | 1.3 |
| V3 | 2 | N3 | 1.4 |
| V3 | 3 | N3 | 1.4 |
| V1 | 1 | N4 | 1.8 |
| V1 | 2 | N4 | 1.9 |
| V1 | 3 | N4 | 2.1 |
| V2 | 1 | N4 | 1.6 |
| V2 | 2 | N4 | 1.3 |
| V2 | 3 | N4 | 1.1 |
| V3 | 1 | N4 | 1.4 |
| V3 | 2 | N4 | 1.5 |
| V3 | 3 | N4 | 1.4 |
| V1 | 1 | N5 | 1.1 |
| V1 | 2 | N5 | 1.4 |
| V1 | 3 | N5 | 1.2 |
| V2 | 1 | N5 | 1.9 |
| V2 | 2 | N5 | 1.6 |
| V2 | 3 | N5 | 1.5 |
| V3 | 1 | N5 | 1.2 |
| V3 | 2 | N5 | 1.1 |
| V3 | 3 | N5 | 1.3 |
Setelah tabulasi data benar, pastikan tiap faktor sudah dibuat menjadi objek data yang benar; lakukan ANOVA dan lihat hasil:
FactRAKL2$Varietas<-as.factor(FactRAKL2$Varietas)
FactRAKL2$Pupuk<-as.factor(FactRAKL2$Pupuk)
FactRAKL2$kelompok<-as.factor(FactRAKL2$kelompok)
aovFactRAKL<-aov(Tinggi~Varietas*Pupuk+kelompok,FactRAKL2)
summary(aovFactRAKL)## Df Sum Sq Mean Sq F value Pr(>F)
## Varietas 2 0.1693 0.0847 4.316 0.0232 *
## Pupuk 4 2.4902 0.6226 31.732 4.95e-10 ***
## kelompok 2 0.0640 0.0320 1.631 0.2138
## Varietas:Pupuk 8 1.0151 0.1269 6.468 8.98e-05 ***
## Residuals 28 0.5493 0.0196
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Operasi-operasi lanjutan, seperti uji asumsi, uji lanjut, ataupun pembuatan plot interaksi, dapat diadopsi dari contoh-contoh sebelumnya.
SumTabRAKFakt<-reshape2::dcast(aggregate(Tinggi~Varietas+Pupuk,data=FactRAKL2,FUN=mean),Varietas~Pupuk,value.var="Tinggi") #(tabel: agregasi, fungsi: baris~kolom)
knitr::kable(SumTabRAKFakt)| Varietas | N1 | N2 | N3 | N4 | N5 |
|---|---|---|---|---|---|
| V1 | 0.9333333 | 1.2333333 | 1.400000 | 1.933333 | 1.233333 |
| V2 | 0.8333333 | 0.9666667 | 1.300000 | 1.333333 | 1.666667 |
| V3 | 0.8666667 | 1.2000000 | 1.366667 | 1.433333 | 1.200000 |
Dan plot interaksinya:
library(phia)
mod2<-lm(Tinggi~Varietas*Pupuk+kelompok,data=FactRAKL2)
im2=interactionMeans(mod2)
knitr::kable(head(im2),n=5) # tabel| Varietas | Pupuk | kelompok | adjusted mean | std. error |
|---|---|---|---|---|
| V1 | N1 | 1 | 0.9600000 | 0.0860909 |
| V2 | N1 | 1 | 0.8600000 | 0.0860909 |
| V3 | N1 | 1 | 0.8933333 | 0.0860909 |
| V1 | N2 | 1 | 1.2600000 | 0.0860909 |
| V2 | N2 | 1 | 0.9933333 | 0.0860909 |
| V3 | N2 | 1 | 1.2266667 | 0.0860909 |
plot(im2) # plot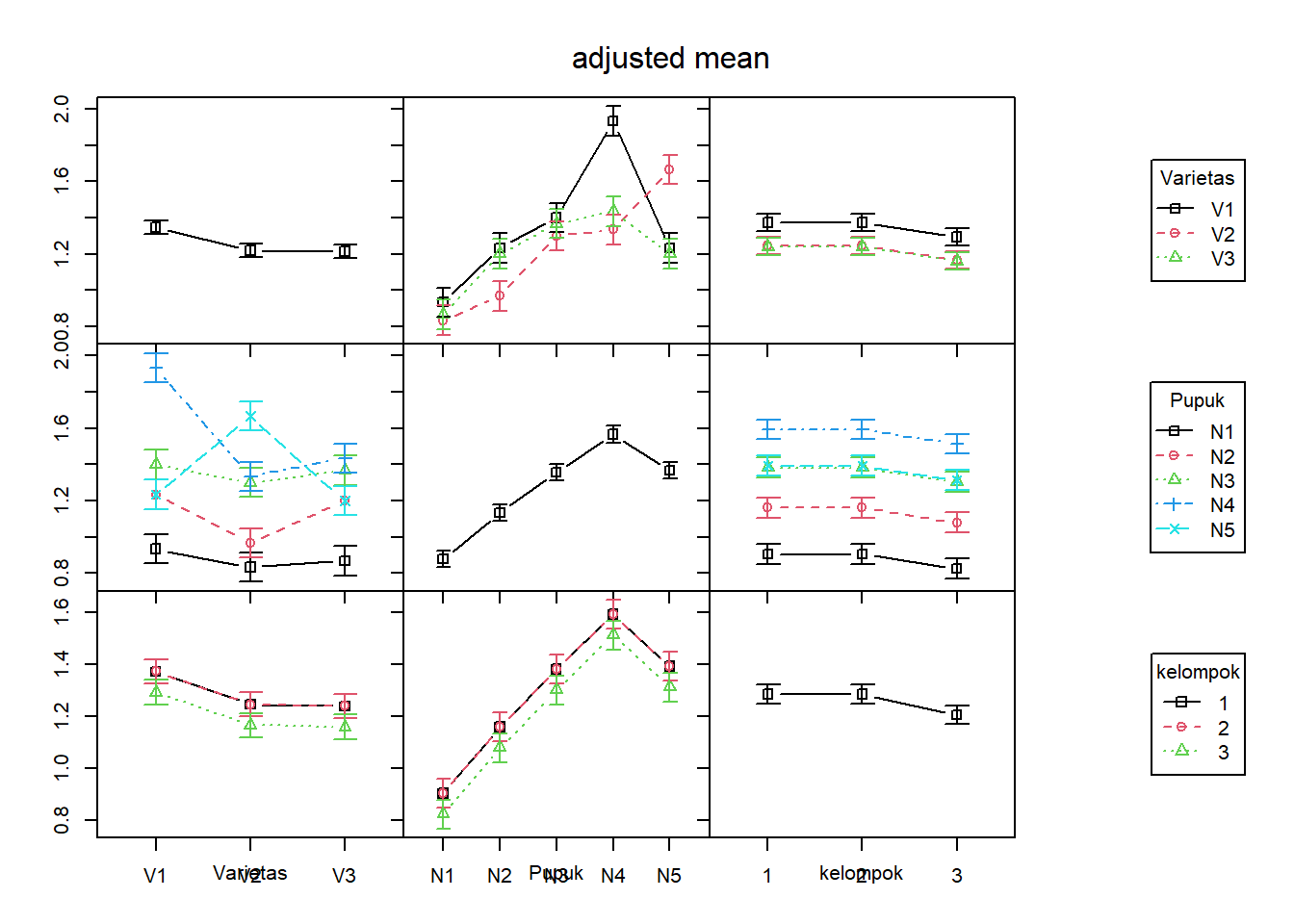
Terlihat bahwa pengelompokan memenuhi asumsi tak ada interaksi.